机器学习中自适应k值的k均值算法改进
2021-01-20钟志峰李明辉
钟志峰,李明辉,张 艳
(湖北大学 计算机与信息工程学院,湖北 武汉 430062)
0 引 言
聚类算法[1-4]中的最常用的一种就是k-means算法[5],该算法最大的特点是简单、好理解、算法复杂度低、运算速度快,在处理大规模数据集时可以保持较好的伸缩性和高效性[6]。但是传统的k-means算法也有很多的缺陷:①k值需要预先确定,但在实际中这个k值的选定是非常难以估计的,若k值过大,则类与类之间的相似度太小,若k值过小,则类与类之间的相似度过大,这两种情况都会导致聚类结果不准确[7];②k-means算法中相似度是以欧氏距离来度量的,因此远离群点的存在对算法结果影响较大[8]。文献[9]提出一种改进k-means算法DMk-means(density mathematics k-means),选取给定邻域范围内最近邻数据点最多的点为初始中心点,可以有效排除远离群点对初始聚类的干扰,但是对于高维数据集效果不佳。文献[10]提出了一种以热扩散的方法来找到数据集的密度峰值,从而发现数据集的聚类中心,虽然提高了聚类效果,但比较复杂。文献[11]提出了用最大距离法选取初始簇中心,使初始簇中心具有很强的区分性,但是初始时可能选取远离群点作为中心点。在分析已有的k-means改进算法的基础上,引进肘部法则的思想对数据进行优化处理,找出远离群点;引入自适应思想并结合误差平方和SSE自动调整k值。结合这几种方法提出一种自适应调整k值的k-means改进算法。最后还与传统k-means算法进行了实验对比,实验结果表明改进后的k-means算法在准确性上和聚类效果上更优。
1 k-means算法改进
众所周知,k-means算法虽然原理非常简单,但是应用非常广泛。而 k-means算法中相似度是以欧氏距离来度量的,因此远离群点的存在对算法结果影响较大。这些缺陷同时也限制了k-means算法的应用。因此上述缺陷的研究是重点。
1.1 根据“肘部法则”的思想对远离群点的改进
由于传统的k-means算法相似度的判定是基于欧氏距离,所以远离群会增大对k值的估计值,增加算法的时间复杂度[12]。为了更加有效地检测出数据集中的远离群点,从而解决远离群点对k-means算法的影响,从肘部法则得到启发,根据其思想找出远离群点,从而达到对算法改进的目的。具体实现如下:
设聚类样本数据集为X={xi|i=1,2,…,m},m为样本数据个数,其中每个样本数据均有n个特征(n>0);将样本数据划分为不同的类别(簇)C={c1,c2,…,ck},k为聚类的个数。
初始时,对样本数据集进行优化处理:将样本数据集X中所有的样本数据当成一个簇,则:
簇中心点
(1)
其中,Cj表示第j个簇所包含的样本数据集合,N(Cj) 表示第j个簇中样本数据点的个数。
计算出X中各个样本数据点到簇中心点μj的欧氏距离集D,具体公式如下
(2)
其中,xi表示第i个样本数据点 (1≤i≤m)。
则D={d1,d2,…,dm}, 根据“肘部法则”的思想,将D中的数据按照小到大排序并得到x-d二维折线图(d为样本数据点到中心点的距离,x为与d对应的样本数据点),距离d增大过程中,畸变程度的改善效果上升幅度最大的位置对应的值就是“肘部”,即“肘部”处满足
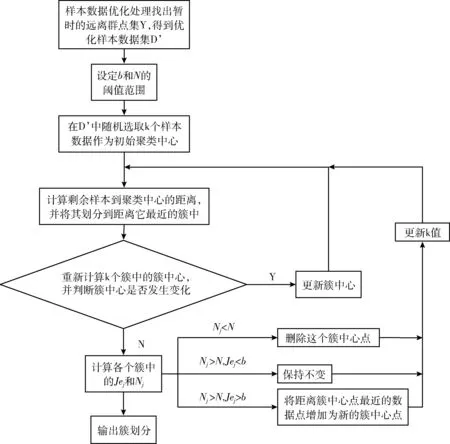
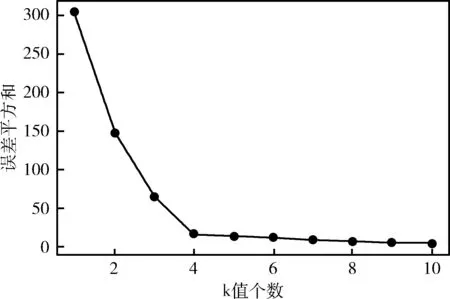
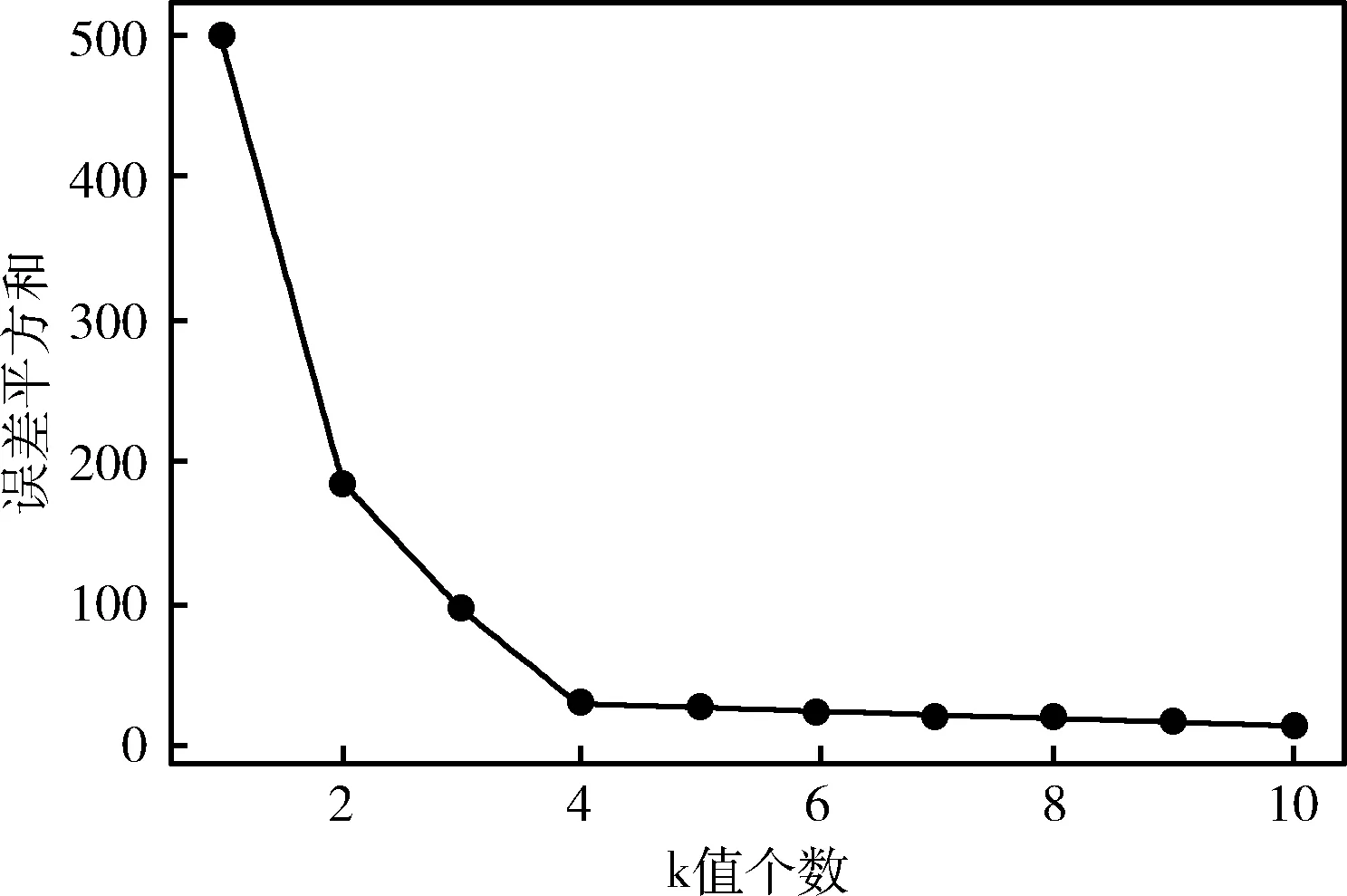
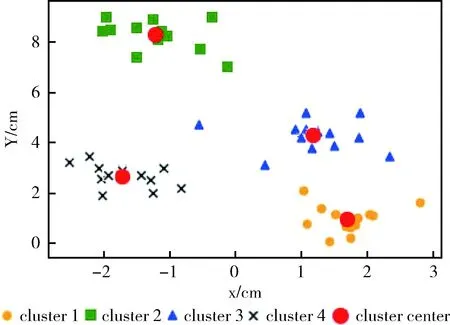
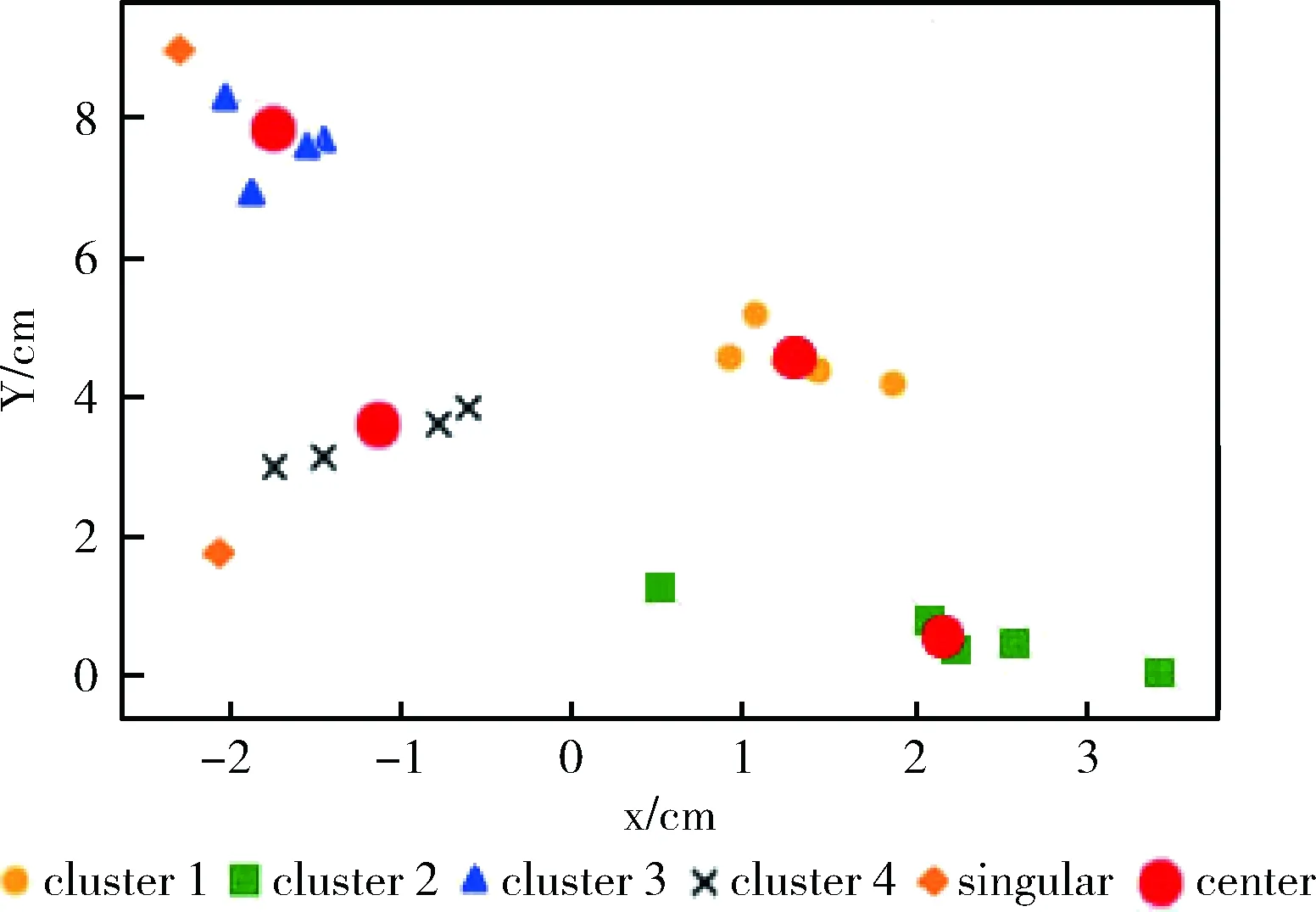
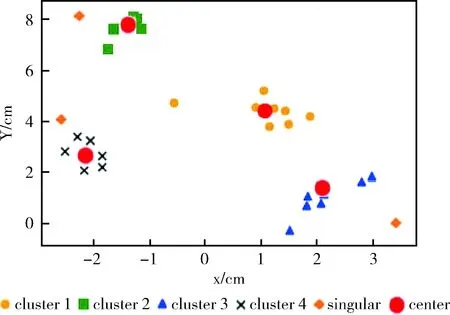
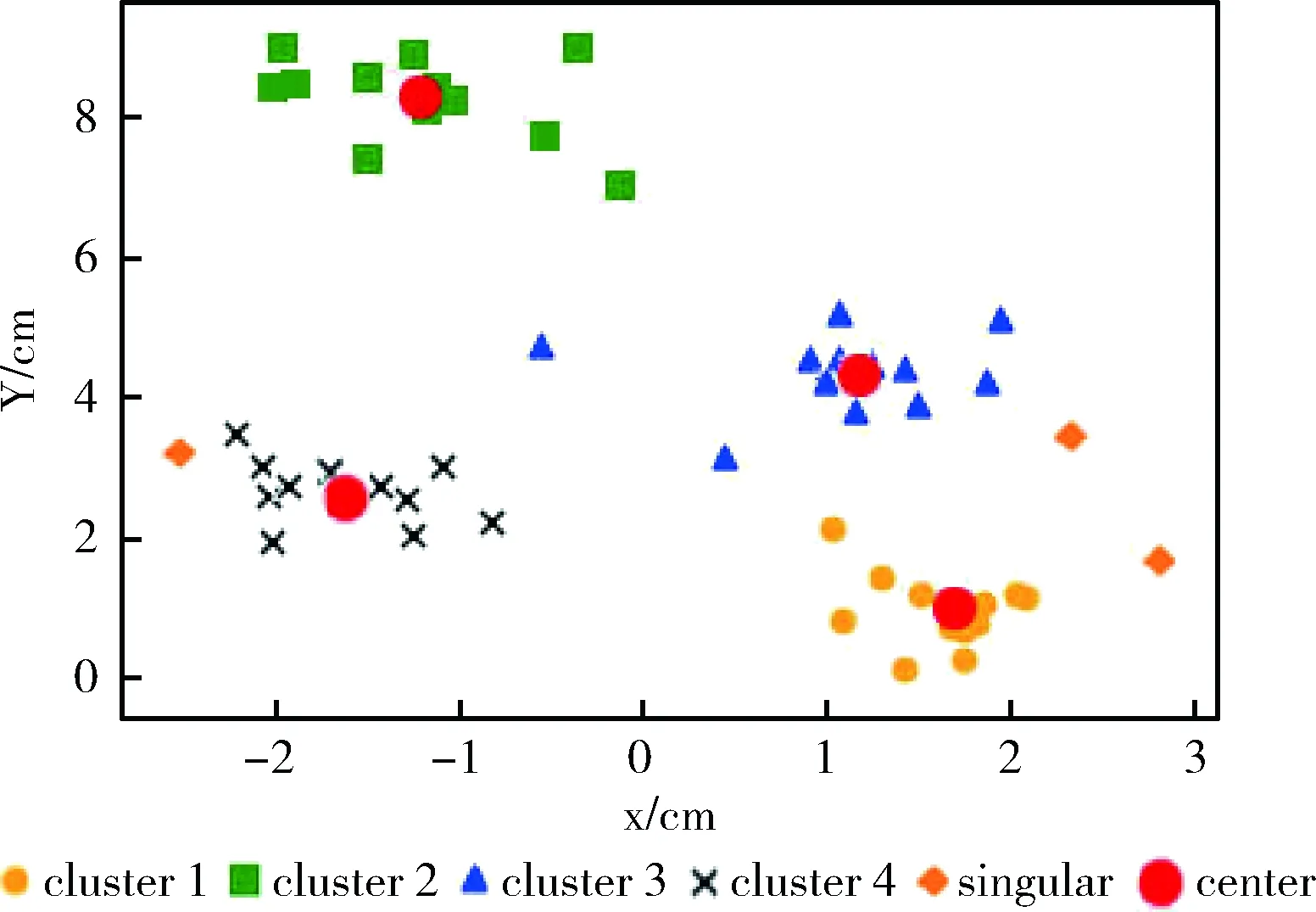
Δd=max(di-di-1) (1 (3) 在“肘部”处进行划分(一般设“肘部”之后对应的数据点个数一般占数据集个数的0%~10%),将距离大于“肘部”点对应距离的数据点暂时定义为远离群点。假设剔除远离群点后还有w个样本数据点(w≦m),则远离群点还有(m-w)个,将非远离群点存放于数据集X’中,并将数据点重新编号,即X’={x1,x2,…,xw}。 将远离群点存放于数据集Y中,并将数据点重新编号,即Y={xw+1,xw+2,…,xm}。 在算法过程中使用的数据集剔除Y中的数据点,即新的样本数据集X’,在算法过程中使用X’数据集进行聚类则可以在一定程度上消除远离群点的影响。 算法完成后簇划分为C={c1,c2,…,cz} (z为簇的个数(算法完成后自适应k值可能会改变)),设第j个簇中簇内数据点到簇中心点的最大距离为maxdj maxdj=max{dj1,dj2,dj3,…} (4) 遍历Y中的数据点xw+1,xw+2,…,xm,根据式(2)计算Y中数据点到各个簇中心点的距离 {(d(w+1)1,d(w+1)2,…,d(w+1)z),(d(w+2)1,d(w+2)2,…,d(w+2)z),…,(dm1,dm2,…,dmz)} (Y中的所有数据点到z个簇的欧氏距离的集合)。若存在第a个簇 (a∈(0,z]), 使集合Y中的数据点xb(b∈[w+1,m]) 满足xb点到a个簇中心点的距离小于该簇中数据点到簇中心点的最大距离,即: (db1 则将xb划分到a个簇中距离它最近的簇 j(xb)=min(db1,db2,…,dba) (5) 若不存在这样的簇,则将该点定义为远离群点。直到Y中所有的数据点遍历完成,即可划分出最终的远离群点。 k-means聚类算法属于非监督的学习方法,传统 k-means 算法选取初始聚类中心是根据自身经验,而对初始聚类中心选取的优化也会引入一定的参数,也会使聚类结果缺乏客观性[13]。引入自适应的思想提出一种自动调整k值的方法。具体实现如下: 聚类评估指标:聚类评估指标有多种多样,选择簇内误差平方和SSE,后文可以根据SSE得出单个簇内聚类评估指标Je,SSE计算公式如下 (6) 其中,k表示簇的个数,x表示样本数据点,μj表示第j个簇的簇中心点,Cj表示第j个簇所包含的样本数据集合。E为k-means算法根据样本X’聚类得到的簇C划分的平均误差平方和,在一定程度上描述了各个簇样本的紧密程度,通常E越小说明聚类效果越好。 由聚类评估指标误差平方和SSE得单个簇内误差平方和Je,公式如下 (7) 其中,xi为第j个簇中的簇内数据点,N(Cj)表示第j个簇中样本数据点的个数,μj为第j个簇的簇中心点。在一定程度上描述了簇内数据的紧密程度,通常Jej越小说明第j个簇的簇内聚类效果越好。 初始时设定簇内聚类评估指标Je和簇内最小数据点个数的阈值N。在各个簇划分完成之后,可以得到各个簇的簇内数据点的个数 (N1,N2,…,Nk); 可以对各个簇根据式(7)进行簇内聚类评估,得到各簇的聚类评估值 (Je1,Je2,…,Jek)。 然后计算出第j个簇聚类评估指标的误差ΔJej和簇内数据点个数与初值的差值ΔNj,具体公式如下 ΔJej=Jej-b (8) ΔNj=Nj-N (9) 结合式(8)、式(9)得出第j个簇中k值变化量 (10) 其中,w为数据集X’中样本数据点的个数,“sgn()”为符号函数,“θ()”为单位阶跃函数,“∏”符号为向上取整。 (1)当Jej>b时,则ΔJej为正数,单位阶跃函数θ(ΔJej)=1, 所以Δkj=Π(logm(ΔJej+1)), 即Δkj>0,即需要在第j个簇中心点附近新增簇中心点来减小簇内误差评估指标。一般0 (2)当Jej 遍历各个簇后,根据式(10)得出k值的变化量 (Δk1,Δk2,…,Δkk), 则更新的k值k’为 (11) 若k’===k, 则终止循环(“===”符号为绝对等于,要求k’与k在数值上和簇中心点位置上都相同); 若k’≠k,则继续循环下去(“≠”要求k’与k在数值上或位置上不相同即可)。 注意:若更新后的k’值与原来的k值在数值上相同,但是簇中心点的位置改变,仍需继续迭代下去。 基于以上两点改进提出一种基于“肘部法则”和自适应调整k值的k-means改进算法。该算法的基本思想是:通过“肘部法则”的思想对样本数据集X进行优化处理,确定暂时的远离群点,算法过程中使用剔除暂时的远离群点的样本数据集,并在算法完成后根据暂时的远离群点与各个簇间的相似度,确定最终的远离群点;通过自适应的思想,在每次迭代完成之后,根据各个簇的簇内聚类评估指标的误差来自动调整k值,直到满足误差范围。 算法改进算法流程如图1所示。 图1 改进算法流程 算法改进算法流程如下: 步骤1 数据优化处理,根据“肘部法则”的思想找出暂时的远离群点并存放在数据集集Y中,得到数据优处理化后新的样本数据集X′={x1,x2,…,xi,…,xw} (具体参考1.1); 步骤2 设定单个簇内评估指标Je和簇内最小数据点个数N的阈值范围; 步骤3 在w个样本数据中,随机选取k个样本作为初始聚类中心 (1 步骤4 根据式(2)计算剩余每个样本数据到聚类中心的欧式距离,并将每个样本划分到距离它最近的簇中; 步骤5 按照式(1)重新计算各个簇的新的簇中心点; 步骤6 若新的簇中心点与原来的中心点相同或者小于某个阈值(收敛定义参考文献[14]),则至步骤7;若新的簇中心点发生改变,则继续重复步骤4、步骤5直到收敛; 步骤7 计算各个簇中的簇内聚类评估Jej和各个簇中数据点的个数Nj。将Jej和Nj与初始设定的阈值范围比较,根据式(10)计算出Δkj。遍历所有的簇后,根据式(11)计算出新的k值k’,若有中心点被删除或新增加,则返回步骤4,直到不再有新增或删除的簇中心点(具体参考1.2); 步骤8 根据数据集Y中的数据点与各个簇的簇中心点的相似度大小来确定最终划分的远离群点(具体参考1.1); 步骤9 输出最终的簇划分C={c1,c2,…,cz}。 这里可以直接调用Python中的sklearn模块[15],其中包含toy数据集和图像样本数据集,toy数据集由一些小批量经典数据集组成,如鸢尾花数据、手写字符数据、糖尿病数据集、波士顿房价数据、健身数据集等等;图像样本数据集由一些小批量经典图像或者模型数据组成,如半环形数据集、圆形数据集、聚类模型随机数据集、分类模型随机数据集、高斯模型随机数据集、回归模型随机数据集等等。采用的是聚类模型随机数据集(make_blobs)来进行验证,见表1。 表1 实验数据 如图2~图10所示,图2~图4分别为聚类模型随机数据集个数为20、30和50,由传统的k-means算法和“肘部法则”结合得出的K-SSE折线图;图5~图7分别为聚类模型随机数据集个数为20、30和50,由传统的k-means算法得出的聚类结果;图8~图10分别为聚类模型随机数据集个数为20、30和50,由改进的k-means算法得出的聚类结果。图2、图3和图4是根据肘部法则得出最合适的k值(由图可知k=4最佳)。对比相同数据情况下由改进的 k-means 算法根据自适应调整k值得出的聚类结果图8~图10,与图2~图4中的k值相同,表明这种自适应k值方法可行。 图2 K-SSE(blobs20) 图3 K-SSE(blobs30) 图4 K-SSE(blobs50) 图5~图7和图8~图10均是在k值相同的基础上得到的,即在改进的k-means算法自适应得出k值之后,再由相同的k值得出传统的k-means算法实验结果,可以使实验对比更加鲜明、实验结果更加准确。对比聚类模型随机数据集且数据集个数均相同的实验结果图5和图8,可以看出图8中比图5中多出了两个远离群点(图中的singular,菱形点),而且簇中心点也有一定的变化,图8中左边两个簇剔除远离群点后,各个簇中的数据更加紧密,聚类效果更优。类似地,图9和图10中的簇中心点也有变化,也剔除了远离群点,明显的改进后的算法聚类后的簇聚合显得更加密集,即改进后的k-means算法的聚类效果比传统的k-means算法更好。 图5 k-means(blobs20) 图6 k-means(blobs30) 图7 k-means(blobs50) 图8 改进k-means(blobs20) 图9 改进k-means(blobs30) 图10 改进k-means(blobs50) 图11是由传统k-means算法和改进后的k-means算法在相同数据集—聚类模型随机数据集blobs,经聚类评估指标SSE得出聚类评估指标的对比。图11中可以看出改进后的k-means算法SSE数据都要小于传统的k-means算法,其主要原因是剔除了远离群点对聚类效果的影响,使得各个簇中的数据集之间聚合更加密集,说明了改进后的 k-means 算法聚类更好。 图11 blobs数据集聚类评估对比 主要是通过研究k-means算法的两个缺陷——对于远离群点特别敏感和k值需要预先确定,在分析已有的k-means改进算法的基础上,对传统的k-means算法进行改进,主要包括对远离群点的处理和自适应的调整k值。并且通过Python中的sklearn模块提供的真实数据集—聚类模型随机数据集进行实验,并将实验结果与传统的k-means实验结果相比较,结果表明改进后的k-means算法中的剔除远离群点自适应调整k值的方法均可行,而且在准确性和聚类效果上有明显的优势。不足的是,簇内聚类评估指标Je和簇内最小数据点个数的阈值N需要根据经验设定,而且改进的算法在循环中嵌套了循环,大大的提高了算法的迭代次数和算法的时间复杂度,对于大量数据的聚类消耗的时间可能过长,需要对数据进行降维等数据优化处理,希望以后能够进一步优化。1.2 根据自适应的思想对k值选取的改进


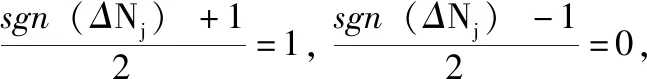
1.3 改进后的算法流程
2 实验分析
2.1 实验数据

2.2 实验结果与分析




3 结束语
