管线点高程自动计算程序设计与应用

张中南

(福州市勘测院 福建福州 350100)

0 引言

城市地下管线探测目的，是为了建设项目在设计过程中让建设项目的管线与市政管线之间能够清晰无误、合理地进行接驳；是为了在城市建设过程中更好地保护已有地下管线，防止施工时对管线造成破坏。目前，地下管线探测手段和技术都比较成熟，相关数据生产软件较为实用。然而，在实际管线勘测及内业生产过程，往往因为数据缺失、现场环境复杂而无法探测、误删属性数据等各种因素，造成管网数据中部分管线高程或埋深值的缺失，尤其是非金属管的管段中央，因为无法用雷达等设备进行探测。

而高程值不完整的数据，在地下管网三维建模、管网流向分析等行业综合应用过程中，会导致管线数据模型不完整，最终出现分析结果出错或者无法分析等问题；另外，管线埋深的缺失，还会影响到道路施工或市政工程中的路面开挖，甚至造成管线挖断等严重后果。为补齐缺失的管线高程数据，常常需要进行外业实地补测，此则不光影响项目工期，还会造成大量人力、物力浪费。因此，研究一种能根据现有的大比例地形图、DEM数据及管线数据，自动计算出缺失管线高程的算法，从而节省大量人力、物力，有着很大的经济效益。

本文研究方法，首先利用管线所在位置的大比例地形图数据内的高程点构建DEM；然后，通过DEM内插，得出管线所在位置的地面高程。同时，利用邻近管线数据，生成一条管线拟合曲线，曲线经过待求的位置，即为管线近似高程。整个算法思路，可以理解为地面是一个曲面，管线为一条曲线，计算位置曲线与曲面之间的距离，即为管线埋深。最后，再结合管线类型、管径大小等信息修正计算，计算出缺失点的管线顶部与地面的近似距离。

1 构建地面高程模型

构造DEM的高程点，可以从大比例地形图提取，根据DEM内插可分为整体内插、分块内插和逐点内插3类[1-3]，每种内插方法，在不同的地形地貌环境下，不同的采样点方式和密度下，都有各自的误差。而地下管线基本在城市内，可以将其视为地貌基本平滑，无较大起伏。而高程点因为来自1∶500地形图，根据国家1∶500外业数字测图规程，高程点最大间隔为15m[4]。故，以管线位置为圆心，半径50 m的缓冲区内提取高程点，基本能满足构建DEM要求，也不会因为结点太多，需要大量的运算。

50 m范围内高程点提取可以满足极大部分情况，但有时管线点处于大型建筑物或是大面积水域旁边，50 m内没有足够的高程点供DEM构建，此时可以按倍数扩大提取范围进行运算。

地图上的高程点，有的由于测图错误或点位置的极端性，会存某些点的高程与周边相差较大的情况，而这些点如果用于DEM，会造成高程波动，影响到内插点的高程精度。因此，为了保证构建DEM过程尽量与实际相符合，在构建DEM前，还应对所有高程点进行比较，筛选过滤出与平均高程值相差较大的点。

2 高程模拟算法设计

管线所在位置地面高程模拟算法设计流程如下：

(1)从管线数据库中，分析出所有需要计算高程值的点位坐标、管线对象和管点对象。

(2)通过点位坐标值，缓冲50 m·N(N从1开始)，获取地形图上的高程点数据。

(3)对所获取的高程点数据，进行计算平均值，设定一个阀值过滤高程值异常的高程点数据。

(4)循环提取任意3个高程点形成三角网，并判断需要计算的高程值点位是否在该三角网内，如果不在三角网内则将其过滤掉。如果在三角网内，则通过以下数学公式计算该点位的高程值。

①通过两点式，计算三角网中的任意两个点(P1和P2)的直线方程A1：(y-y1)/(x-x1)=(y-y2)/(x-x2)；

②通过两点式计算三角网中的另一点(P3)和待计算的点位(P)形成直线方程A2：(y-y3)/(x-x3)=(y-y′)/(x-x′)；

③通过直线方程A1和A2，求解两条直线的交点值PT(XT，YT)；

④计算长度L1(P3-PT)和L2(PT-P)，计算长度比例△K=L1/L2。

⑤通过长度比例△K和P3的Z3值，最终计算出P点位的Z值(Z=Z3*△K)；

⑥通过上述的计算，取得一组该点位上的高程值数组，并判断该数组是否达到阀值数M；如果未达到，则N=N+1重新计算。

⑦去掉高程值数组中的最大值和最小值，最终计算高程的平均值H。

具体算法设计图如图1所示。

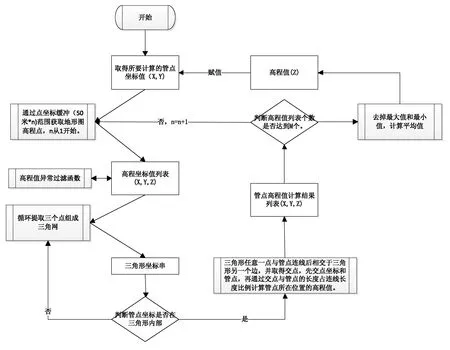
图1 高程模拟算法设计图

任意三角形内计算管点的高程值相关代码如下：

public class MathsClass

{

///

/// 通过3个点组成的三角网，计算内部第四个点的高程值；如果第四个点不在三角网内，返回-99999。

///

public void GetAltitudeValue(PointStruct Point1, PointStruct Point2, PointStruct Point3,ref PointStruct MidPoint)

{

MidPoint.Z = -9999;

PointStruct pCrossPoint = GetCrossoverPoint(Point1, Point2, Point3, MidPoint);

bool bIsIn = IsInLine(Point1, Point2, pCrossPoint);

if (bIsIn == false) return;

CalculationAltitude(Point1, Point2, ref pCrossPoint);

bIsIn = IsInLine(Point3, pCrossPoint, MidPoint);

if (bIsIn == false) return;

CalculationAltitude(Point3,pCrossPoint, ref MidPoint);

}

///

/// 按比例计算高程值

///

private void CalculationAltitude(PointStruct Point1, PointStruct Point2, ref PointStruct MidPoint)

{

double dA = -99999;

double dK = (Point1.X - MidPoint.X) / (MidPoint.X - Point2.X);

dA = (Point1.Z + dK * Point2.Z) / (dK + 1);

MidPoint.Z = dA;

}

///

/// 取得三个点组成的三角网，与第四个点的连线的交点坐标

///

private PointStruct GetCrossoverPoint(PointStruct Point1, PointStruct Point2, PointStruct Point3, PointStruct MidPoint)

{

PointStruct pCrossPoint = new PointStruct();

double x = 0; double y = 0;

x=(Point3.Y-Point2.Y)*(Point2.X-Point1.X)*(MidPoint.X-Point3.X)+Point1.X*(MidPoint.X-Point3.X)*(Point2.Y-Point1.Y)-Point3.X*(Point2.X-Point1.X)*(MidPoint.Y-Point3.Y);

x=x/((MidPoint.X-Point3.X)*(Point2.Y-Point1.Y)-(Point2.X-Point1.X)*(MidPoint.Y-Point3.Y));

y=((Point2.Y-Point1.Y)*(x-Point1.X))/(Point2.X-Point1.X);

y=y+Point1.Y;

pCrossPoint.X=x;

pCrossPoint.Y=y;

return pCrossPoint;

}

///

/// 判断交点是否在线段上

///

private bool IsInLine(PointStruct Point1, PointStruct Point2, PointStruct CrossPoint)

{ //通过坐标值判断

return true;

}

}

3 地下管线曲线模拟

管线外业探测时，除了测量每个井的管线高外，在两井相隔较远的地方，也会在中间加密管线点。因此，在某个要推算埋深的管线位置，两端一般都有管线已知高程。

在理想的情况下，待算位置两端各取最近的一个有高程的管线点，两个点相连形成一条直线，直线经过待算位置点的三维坐标，即为待求点坐标。但实际应用中发现，这个情况只适用于铸铁管、PC管等硬管，对于电缆、光缆等软性管，直接用直线取值会有一定的误差，特别是使用拉管施工下穿马路、河流等管线上，直线存在较大的误差，这时就需要用其他办法。

本文采取的方法为，在待求位置两端各取3～5个已知管线点，通过最小二乘法建立拟合曲线[4-6]，曲线经过待求管线位置的三维坐标，即为该管线点的坐标。

4 算法检验

算法程序编写完成后，笔者抽取某市建成区市政道路旁绿化带里的一条给水管线以及新区未开发区域(地貌起伏变化较大)的一条给水管线分别进行试验，对未能探出管线埋深的点位进行开挖验证；同时结合1∶500DLG数据，采用程序对试验点的埋深进行计算。计算结果与实际埋深对比结果如表1所示。

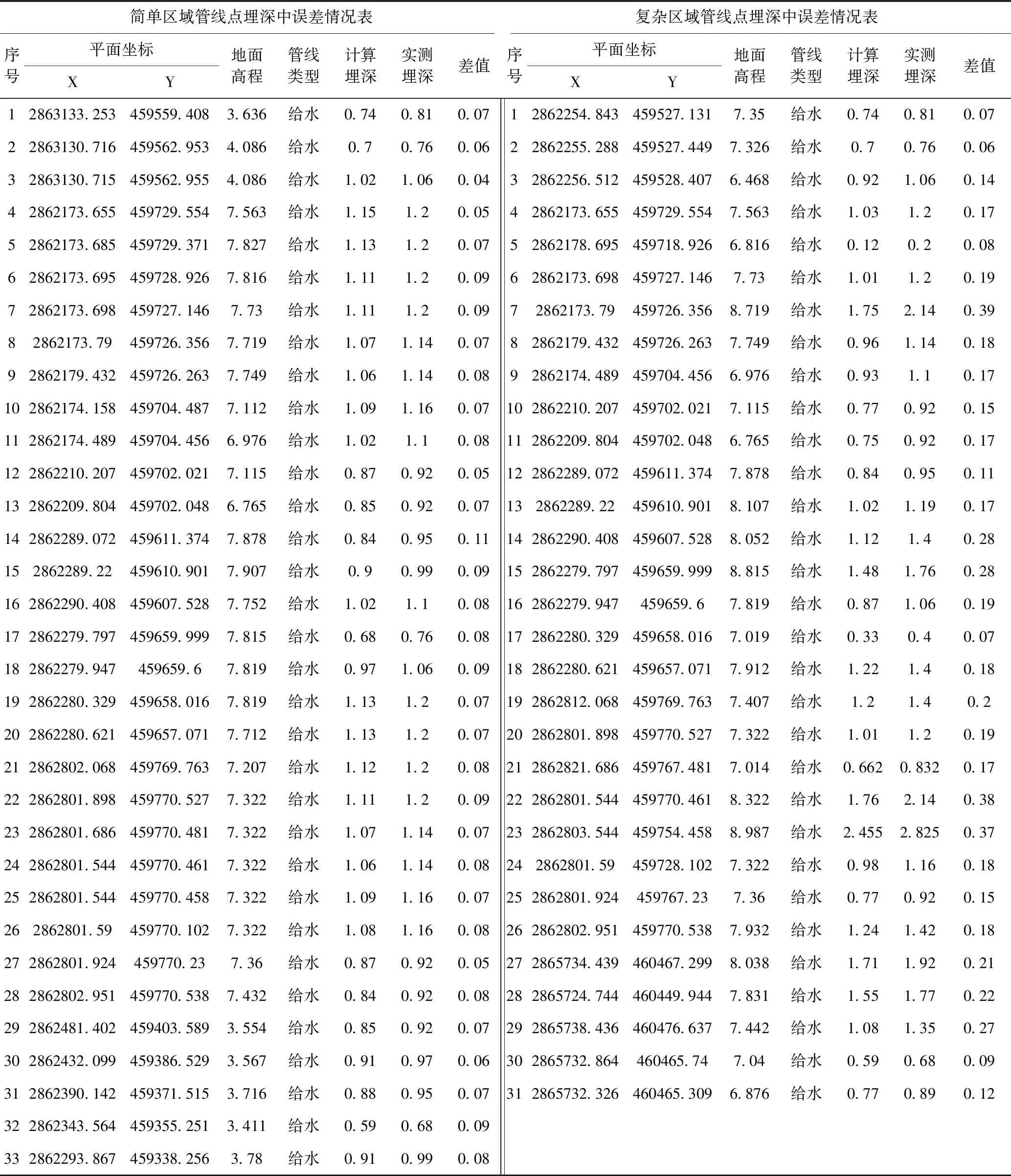
表1 计算结果与实际埋深对比结果表 m

(1)简单区域管线点埋深误差情况分析表明：本算法计算出的埋深与实测埋深相差最大值为0.11m，最小值为0.04，平均值为0.074m，根据《城市地下管线探测技术规程》(CJJ 61-2017)及《工程测量规范》(GB50026-2007)规定，隐蔽管线点埋深探查中误差不大于0.075h(当h<1000mm时，以1000mm代入)，本算法所计算出的管线点埋深，符合《城市地下管线探测技术规程》及《工程测量规范》。

(2)复杂区域管线点埋深误差情况分析表明：本算法计算出的埋深与实测埋深相差最大值为0.39m，最小值为0.06，平均值为0.186m，根据《城市地下管线探测技术规程》(CJJ 61-2017)及《工程测量规范》(GB50026-2007)规定，隐蔽管线点埋深探查中误差不大于0.075h(当h<1000mm时，以1000mm代入)，本算法所计算出的管线点埋深，部分超出符合《城市地下管线探测技术规程》及《工程测量规范》。

综上分析可见，利用本算法计算埋深时，应区分区域地形地貌情况，在地形比较平坦区域，本算法计算埋深可适用；在地形复杂区域，本算法计算出的埋深与实际埋深的误差可能会超限。

5 结语

挖断或打穿地下管线的事例，在市政施工及道路开挖中屡见不鲜，本文提出的充分利用已有地形数据及管线数据，模拟计算管线埋深的方法，对难以探测位置的管线定位具有较大的参考价值。

由于本文所提算法需要计算点位置周边大量地形与管线数据支撑，所以在数据比较完整的城市地区应用效果比较好；而对地形和管线数据稀少的区域，则应用价值不大。

其次，地形环境的不同，对本算法也有较大的影响，在地面起伏不大的地区计算结果较好，而地形变化明显、沟坎纵横的地区，往往会出现较大偏差。在工程施工中，重要管线埋深应到现场进行重新探测确认。