基于博弈论的信息物理系统在FDI攻击下的控制
2021-01-20李庆奎
王 羽, 李庆奎
(北京信息科技大学自动化学院,北京 100192)
信息物理系统(Cyber-Physical System,CPS)是将3C技术(计算、通信、控制)与现代物理设备完美结合,通过嵌入式计算机对物理过程进行感知和控制的智能系统[1]. 与传统控制系统相比,CPS更加可靠、高效、实时协同. 但因为CPS中有大量用于通信的设施和IT组件,所以CPS更容易遭受网络攻击[2-3].
CPS的网络攻击主要分为两类:完整性攻击和可用性攻击[4]. 完整性攻击是指通过篡改传输数据包中的信息,以降低系统可靠性和安全性的攻击方式[5]. 可用性攻击则可阻断CPS各部分之间数据、控制命令的正常传输,使某些服务被暂停甚至使系统瘫痪. 虚假数据注入(False Data Injection,FDI)攻击是一种完整性攻击方式,通过劫持物理设备(传感器、控制器等)或者网络信道,向系统注入错误或无用但存在安全隐患的数据信息,破坏数据的完整性,导致系统失去稳定甚至崩溃[6]. 与其他网络攻击相比,FDI攻击更加巧妙、复杂并具有更高的隐蔽性. 针对信息物理系统FDI攻击的研究大致可以分为以下三类[7].
第一类,FDI攻击的可行性分析、实现路径和方法研究. 文献[8]研究了攻击不被检测的基本条件,给出了系统可被攻击的传感器的最小数量,以确保攻击的隐蔽性;文献[9]在所有传感器数据可观且可以被攻击者修改的情况下,提出了一种对远程状态估计器发起线性欺骗性攻击的策略,该策略可以成功通过卡方检测器的监测;文献[10]将攻击者的控制目标表示为一个二次型值函数,通过求解约束优化问题来寻找最优攻击策略.
第二类,从防御角度出发制定系统保护机制、入侵检测机制并降低攻击影响. 文献[11-12]采用卡尔曼滤波器来估计状态变量,并设计了相应的检测器来发现未知传感器子集上的攻击信号,但都过于关注误差的统计特性而忽略了CPS的高速采样特性. 基于此,文献[13]将欧氏检测器、卡方检测器以及卡尔曼滤波器结合起来设计了针对智能电网系统的安全框架,该方法可以克服以上缺点但只适用于电网电压信号模型;文献[14]借助线性二次型控制理论,开发了最优自适应切换策略通过来抵御稀疏的传感器-执行器攻击策略.
第三类,研究攻击-防御对抗策略. 这类研究的目的是揭示网络攻击方的行为特征及量测系统的脆弱点,为量测系统的安全防护工作提供参考依据[15]. 网络攻防对抗的本质可以抽象为攻防双方相互博弈的过程. 现有网络攻防博弈策略研究文献甚少,且大多集中于网络安全领域[16-18],很少有关于物理系统的控制安全分析. 文献[19]从网络安全的角度出发,提出了一种基于非合作、完整信息的博弈主动防御模型,通过解决不同系统状态下的纳什均衡,实现最佳防御策略. 不足之处在于在网络对抗中使用完全信息静态博弈模型,与实际的应用场景不够贴切. 文献[20]以电力CPS为背景,建立了三层动态攻防博弈模型,并用遍历思想结合遗传算法求解该方案. 但该方法只适用于电网负荷数据被攻击的情况,不适用于一般的线性模型.
与上述文献的研究侧重点不同,本文着重考虑FDI攻击对控制系统的影响,采用攻防博弈模型研究控制安全问题. H∞范数被广泛用于描述控制对信号的抑制程度. 针对受FDI攻击的信息物理系统,在设计控制器时首先建立H∞目标函数和约束条件. 借助最优控制的理论和方法,将H∞问题抽象为二人零和博弈问题并求出其均衡解. 通过纳什均衡设计状态反馈控制器,使系统在保持鲁棒稳定性的前提下最大限度地降低攻击对状态的影响,获得最优的性能指标. 而后对系统矩阵未知的情况展开研究,设计无模型状态反馈Q学习算法,利用系统的量测数据在线求解最优控制策略和最坏情形攻击策略. 使系统在没有动力学知识的情况下,控制性能达到最优. 最后通过算例仿真证明了提出方法的可行性.
1 问题描述
1.1 系统模型
考虑FDI攻击下的线性时不变信息物理系统:

其中,xk∈Rn,uk∈Rm1分别是k 时刻的系统状态变量和控制输入信号,ak∈Rm2是攻击者在有限时间[0,T]内向系统注入的攻击向量,且ak∈L2[0,∞) . 矩阵(A,B,C)是未知恒定的具有适当维数的系统矩阵.
假设1 FDI攻击者具备以下几点攻击能力:
1)攻击者知道系统(1)的线性结构,但无法获取参数矩阵(A,B,C)的准确值.
2)攻击者可以获取控制信号uk和状态信息xk.
3)攻击者可以产生一个无约束的攻击信号ak对传感器发起虚假数据注入攻击.
为了保障CPS的安全,本文采用H∞范数来评价CPS对攻击的鲁棒性.
定义1 H∞控制的目标是:
1)找到合适的控制输入使得系统(1)在ak=0 的情况下渐近稳定;
2)当攻击者发起攻击即ak≠0 时满足

式中,Q 和R 是正定对称的权重矩阵,γ ≥0 为给定的衰减因子. 上式是反映系统对攻击的鲁棒性评价. γ 越小,说明系统对攻击的抑制效果越好.
基于式(2),首先对系统(1)定义一个性能指标函数:
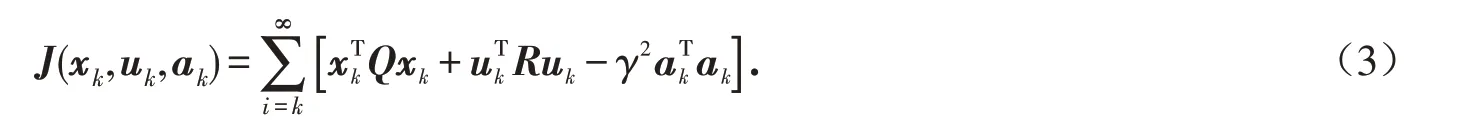
对于容许的控制输入和外部攻击信号定义如下值函数:
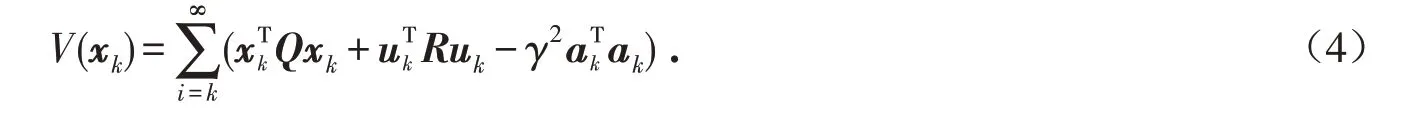
假设2 (A,B)是能控的,(A, Q)是能观的.
1.2 将H∞控制问题转化为二人零和博弈问题
H∞控制问题可看作是一个零和博弈问题,其中参与者包含控制器和FDI攻击信号,控制输入的目标是尽可能减小指标函数,而攻击信号的目标则是最大化指标函数. 因此,这个过程可表示为

且满足

注1 式(14)~(16)是二人零和博弈问题(5)的解,并且保证了当攻击ak≠0 时系统满足H∞指标(2).式(17)是保证系统稳定的充分条件.
1.3 无模型状态反馈Q学习算法
在这一节中,将提出无模型Q 学习算法在线求解在系统矩阵(A,B,E)未知时的最优控制策略增益L*和最坏情形攻击策略增益K*.
仿照式(8)的形式定义Q 函数:

将式(1)代入式(18)并将其写成矩阵形式:

式中,

当系统矩阵已知时,令式(19)的一阶偏导满足∂Q(xk,uk,ak)/∂uk=0,∂Q(xk,uk,ak)/∂ak=0 即可求出最优控制增益L*和最坏情形攻击增益K*的解:
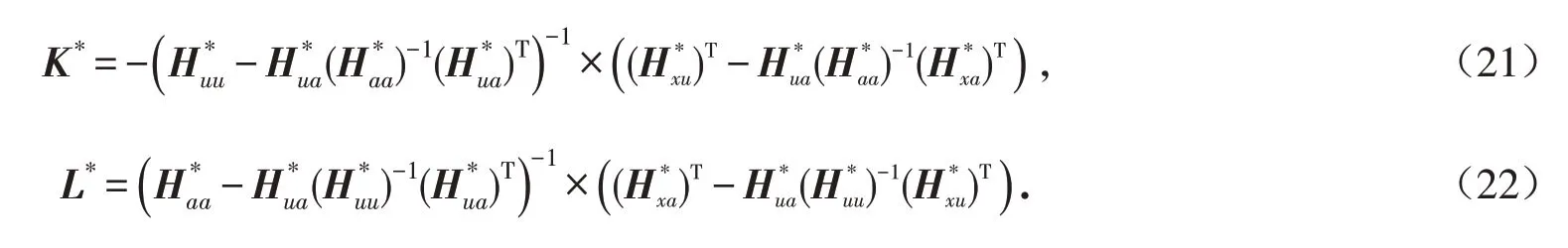
注2 式(21)、(22)中最优控制策略增益L*和最坏情形攻击策略增益K*的解由参数矩阵H 的元素构成,而矩阵H 的元素又由系统矩阵(A,B,E)构成. 当系统矩阵(A,B,E)未知时,无法通过对式(19)求一阶偏导从而求出最优控制策略增益L*和最坏情形攻击策略增益K*.
因此,下面将借助强化学习中的Q学习算法,利用系统的量测数据在线学习出参数矩阵H 的值.
根据值方程(8)和Q 方程的定义式(18)可知:

式(18)则可以表示为:

基于式(24)定义贝尔曼时间差分误差:
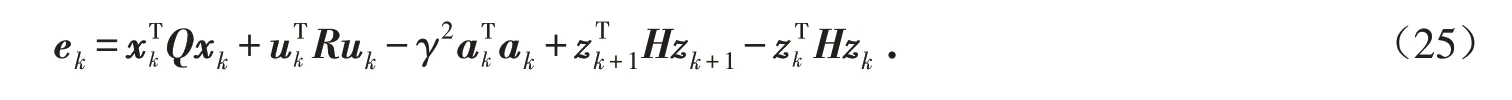
接下来将用式(21)、(22)、(25)驱动无模型Q 学习算法. 算法包括策略评估和策略改进两步,其中策略评估步骤将控制策略、攻击策略固定,对参数矩阵H 进行估计;策略更新步骤则利用第一步计算出的矩阵H,改进控制策略、攻击策略. 算法具体步骤如表1所示.

表1 无模型状态反馈Q学习算法Tab.1 Model-free state feedback Q-learning algorithm
在策略评估阶段,利用最小二乘法估计参数矩阵H. 根据克罗内克积,式(26)可化为

令

代入到式(29)中可得到

2 算例仿真
在本节中,将用F-16飞机自动驾驶仪来验证所提算法的有效性,系统的动力学方程为


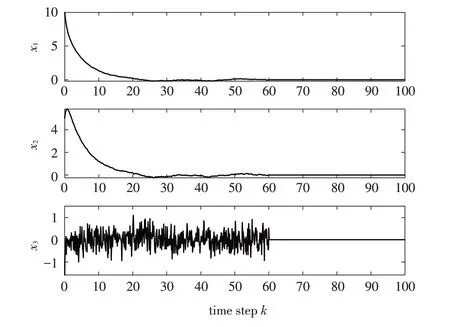
图1 F-16飞机状态xi 的响应曲线Fig.1 State response of F-16 aircraft state xi

图2 参数矩阵H 的误差响应曲线Fig.2 Error response of parameter matrix H
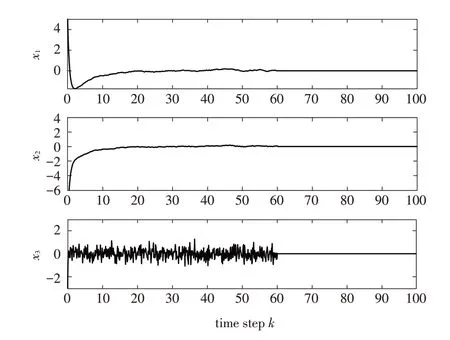
图3 不同初始条件下F-16飞机状态xi 的响应曲线Fig.3 State response of F-16 aircraft state xi under different initial conditions
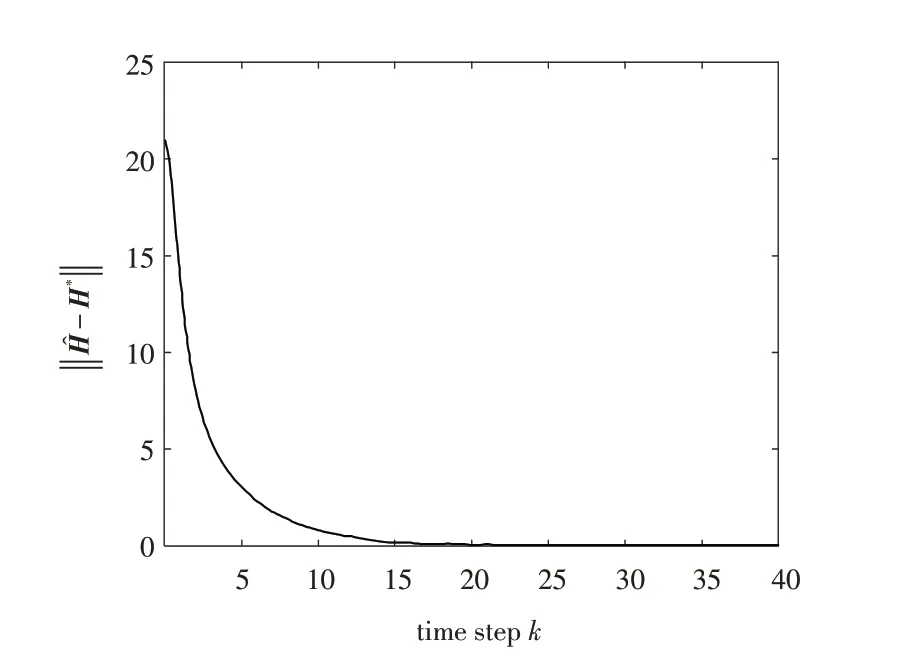
图4 不同初始条件下参数矩阵H 的误差响应曲线Fig.4 Error response of parameter matrix H under different initial conditions
3 结语
本文利用二人零和博弈的思想,研究了信息物理系统在系统矩阵未知且受FDI攻击影响下的H∞控制问题. 首先对系统提出鲁棒稳定性的要求,建立二次型H∞目标函数,而后将H∞控制问题转化为二人零和博弈问题,并推导出最优控制策略和最坏情形攻击策略. 最后,设计在线无模型状态反馈Q学习算法求出最优控制策略和最坏情形攻击策略. 仿真结果验证了该方法行之有效,考虑到同时具有扰动和攻击的CPS会更加贴切实际情形,可以作为下一步的研究方向.
