CAES储气库设计参数对其热力学特性影响

万 发，蒋中明,2，唐 栋,3

（1长沙理工大学水利工程学院；2长沙理工大学水沙科学与水灾害防治湖南省重点实验室；3长沙理工大学洞庭湖水环境治理与生态修复湖南省重点实验室，湖南 长沙410114）

间歇性和不稳定性是太阳能、风能、潮汐能等清洁可再生能源并入电网使用的主要障碍，压气储能(compressed air energy storage，以下简称CAES)技术是解决该问题的大规模储能技术[1-5]。CAES 电站储气库洞室作为能源存储装置，其安全性和稳定性是电站稳定运行的基础，揭示储气库洞室内部热力学特性[6]，对于评价储气库洞室的安全性和稳定性意义重大。

在研究CAES 储气库热力学特性方面国内外学者已经进行了很多研究，并取得较多成果，如Raju[7]、Kushnir[8]、Zhou[9]、Xia 等[10]学者用数学解析解的方式建立了温度、压力解析方程，研究了洞室内气体热力学变化过程，但解析解的计算结果为洞室内部温度压力的均值，并不能描述温度、压力、能量在洞室空间内部分布规律。德国Huntorf 电站给出储气库洞室温度压力实测值时，指出洞室内温度和出口处温度在运行过程中存在差异[11]，根据Geissbühler 等[12]在瑞士南部的实际试验和蒋中明等[13]在湖南平江储气室试验结果以及刘佳的研究[14]都表明地下储气库洞室内部温度、换热器TES 内温度在空间分布上有着较大差异性。储气库洞室内部不均匀温度场会导致围岩受到不均匀温度应力，极端情况下甚至会在洞室局部区域形成极高温区域，引起洞室围岩和衬砌产生热损伤破坏。因此对储气库洞室热力学特性分布规律的研究可有效指导储气库洞室设计，避免出现极端不均匀温度场而引起的热力学破坏。

He 等[15]通过存储㶲值的计算了不同传热边界下的洞室库容。确定库容后需要选择适合的洞室形式，夏才初等[16]研究了隧道式和大罐式洞室的内压下围岩力学特性。确定库容和洞室形式后，仍有不同的长宽设计方案，不同洞室设计方案对于洞室热力学特性的影响却未见报道。

为揭示CAES 储气库洞室运行过程热力学特性分布规律，研究不同洞室设计方案对热力学特性的影响，本文拟采用COMSOL 非等温共轭传热模型，模拟Huntorf 电站单储气库日循环运行过程，并采用实测数据对模型方法进行验证，同时进一步对圆柱形洞室不同体型参数和入气口布置位置工况进行建模，模拟其充气过程的洞室热力学变化过程，对比分析不同设计参数对洞室热力学时空分布特性的影响，为洞室的设计提供依据。

1 压缩气体流动热力学理论分析

本文研究气体在洞室内部流动和传热状态时，基于以下假设：①由于充气口进入的气体流速较高，因此假定储气库内气体流动状态服从标准湍流k-ε 双方程模型；②气体具备可压缩性，压缩气体的温度压力满足气体状态方程；③热对流过程除强制对流外考虑自然对流，储气过程中，温差和重力导致储气库内气体流动；④计算流动加热时忽略气体的黏性耗散；⑤储气库洞壁围岩热传导过程满足傅里叶定律。

流体连续性方程(1)和湍流k-ε 二方程(2)～(3)

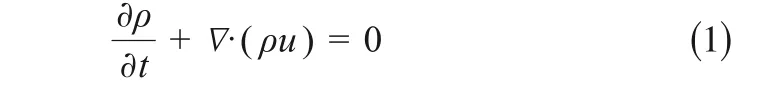
式中，ρ 为气体密度，kg/m³；▽为汉密顿算子；u 为速度矢量，m/s。

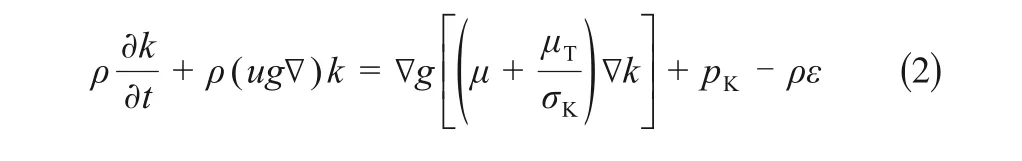
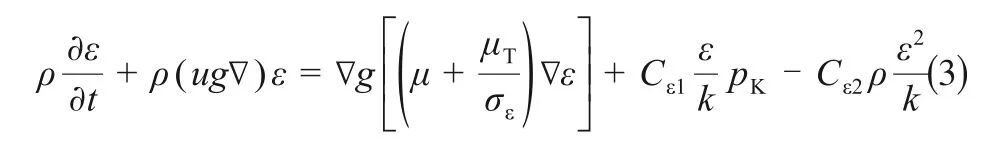
式中，pK为湍流速度变化所引起的压力，Pa；μT=ρCμk2/ε 湍流黏度系数；ε=ep 为湍流脉动动能耗散率；常数Cμ=0.09；σε=1.3；Cε1=1.44；Cε2=1.92。

洞室内气体流动过程中的能量主要由流入过程中的动量、气体压缩做功产生的能量变化、热量向洞壁传递过程三个主要部分组成，其中气体流动的动量控制方程为

气体压缩做功的能量控制方程

式中，Qp为气体压力做功，J；T 为温度，K。

热传导方程

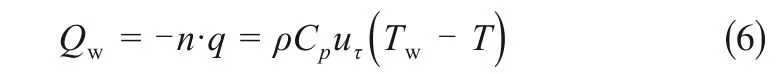
式中，Qw为气体固体传热流量，J/S；q 为界面处热流密度，J/s；uτ为壁面处综合摩擦系数；Tw为固体壁面温度，K；T 为流体温度，K。

为研究洞室内能量存储状况，采用文献[15]中㶲值计算方法来计算能量存储㶲

式中，m 为充气速率，kg/s；cp为气体恒压比热容；T 为洞室内气体温度，K；T0为气体初始温度，K；p 为洞室气体压力，Pa；p0为气体初始压力，Pa。

2 理论模型验证：Huntorf 储气库为例

2.1 验证模型参数及计算条件

为验证理论模型的正确性，采用德国Huntorf电站给出的实测数据做对比。Huntorf 电站采用地下盐岩溶腔作为储气库洞室，由于其洞室边界实际的不规则性，此处将洞室简化为圆柱形洞室。采用COMSOL 软件湍流和流固传热模块并耦合非等温流进行建模计算，洞室模型网格示意图如图1 所示，共有域单元77794 个，模型半径为67.24 m，其中围岩厚50 m，模型分为两个域，内部洞室为流体域，外部围岩为固体域。流体域顶部布置入气口，针对湍流模型：充气入口处为流量边界，流体域外边界为0 通量边界；针对流固传热模型：充气入口为温度边界(充气段)、绝热边界(储气段)和流出边界(放气段)，围岩外边界为绝热边界，采用“层壳”导热的方式处理传热场的流体固体交界面。采用分离求解器PARDISO 求解算法进行求解，收敛条件为容差控制，相对容差为0.005。洞室和围岩物理性质参数如表1 所示。Huntorf 电站的日循环运行过程包含了三种运行状态的交替往复，分别为放气状态、储气状态、充气状态，储气室各个运行状态的时间和充放气体流率如图2 所示。为简化计算，第一个小时的放气速率简化为150 kg/s 均匀放气，其中3 个充气阶段的充气温度分别为50.96 ℃、45.95 ℃、49.08 ℃。

2.2 验证模型计算结果及其验证

图1 洞室有限元模型网格示意图Fig.1 Sketch of FEM meshes of Huntorf cavern

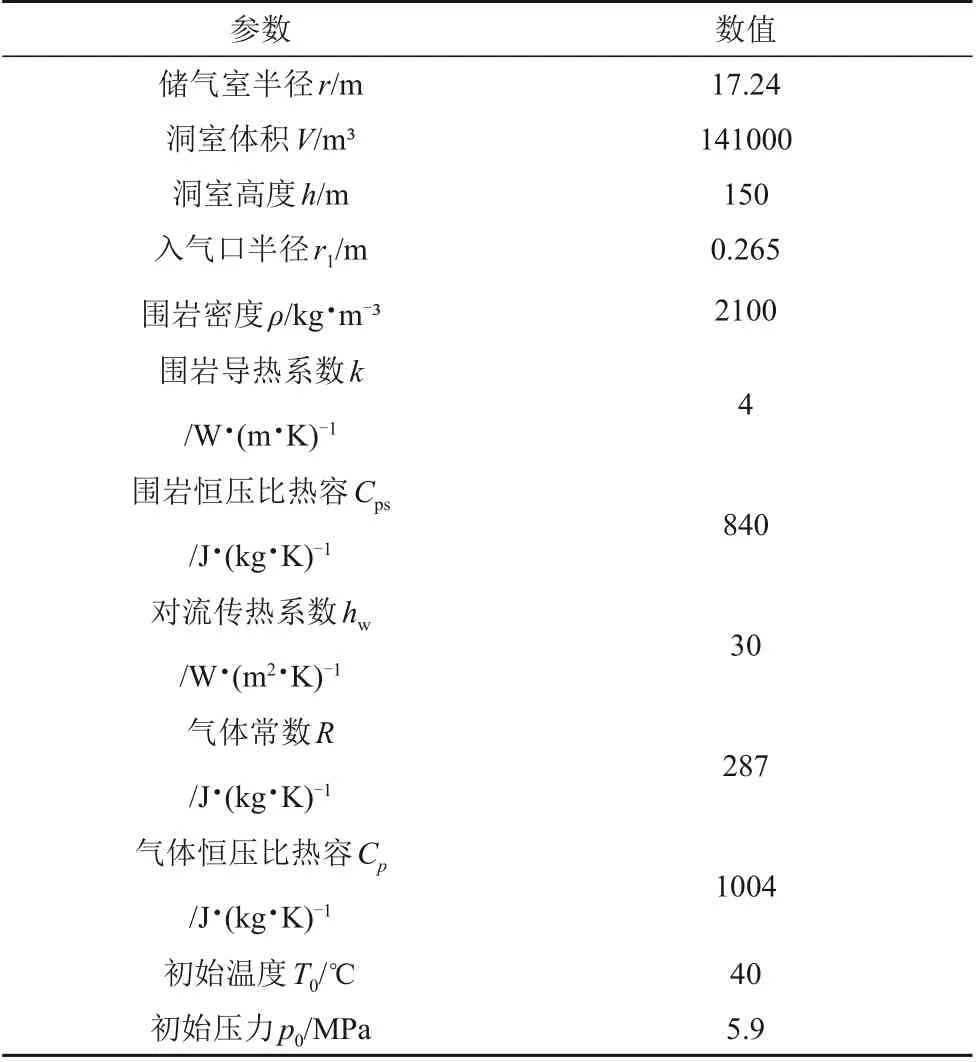
表1 Huntorf压气储能电站储气库参数[8,10]Table 1 Parameters of Huntorf CAES plant[8,10]

图2 洞室日循环运行充放气速率Fig.2 Mass flow rate of air to the cavern in daily circulation

Huntorf 日循环过程洞室内气体温度随时间变化规律以及与文献[16]给出的实测值对比结果如图3 所示，由于三维洞室内温度场不均匀性的存在[16]，其中温度分别考虑了洞室内部气体温度均值，以及洞室与围岩界面处温度均值；洞室内气体压力随时间变化规律以及与文献[16]给出的实测值对比结果如图4 所示，气体压力也考虑了洞室内部压力均值和界面处压力均值。由图可知，洞室温度模拟结果中，界面温度均值与实测值拟合结果比整个洞室内温度均值的拟合结果好，但在第二段充气结束时刻界面温度均值与实测值有着3 K 的差异，随后的储气段和充气段前期都有着2～3 K 差异。气体压力在洞室内部均值和界面处均值与实测值之间的拟合结果较好，该模型可以较好地模拟洞室内气体压力的变化。

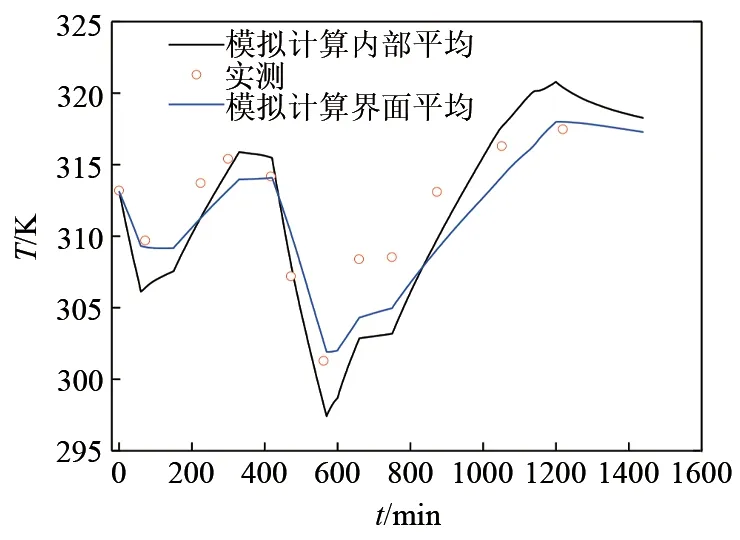
图3 洞室气体温度模拟结果与实测对比Fig.3 The comparison between simulated air temperature and measured value of the Huntorf cavern

图4 洞室气体压力模拟结果与实测对比Fig.4 The comparison between simulated air pressure and measured value of the Huntorf cavern

由以上模拟结果与实测对比可知，该模型可以较好地模拟CAES 电站充放气过程中洞室气体压力变化过程，对于温度而言，由于三维模型温度空间不均匀性，模拟计算结果与实测值之间的误差是在可接受范围之内的。总而言之，该模型可以较好地模拟计算CAES 洞室内热力学特性变化规律。

图5 最佳拟合点温度变化规律Fig.5 Validation of the best fitting point of air temperature

3 洞室设计方案对热力学特性时空分布影响

CAES 储气库洞室涉及热力学过程复杂，其中充放气速率、温度、运行压力，库容估算等都有据可循，但是确定库容之后的设计方案对洞室内热力学特性的影响结果却仍不清楚。为研究不同设计方案对洞室内热力学特性影响，本文研究竖直圆柱形洞室不同体型参数K(洞室长度与洞室半径之间比值)和不同入气口位置对洞室内热力学特性的影响。

3.1 储气库体型参数对压缩空气热力学特性空间分布的影响

为研究圆柱形洞室体型参数K和不同入气口位置对洞室内热力学特性的影响，拟设置4 种不同K值和两种入气口布置形式共五种的工况，五种洞室设计方案变量参数如表2所示。五种方案下洞室体积为2500 m³，洞室围岩研究半径30 m，模型分为两个域：内部流体域，外部围岩固体域。围岩固体域外边界采用开放式边界，等于大气温度20 ℃，初始温度为20 ℃，初始压力为1 atm(1 atm=101.325 kPa)，充气速率为10 kg/s，充气温度为10 ℃，其他模型参数如表1 所示。K=10 时模型如图6所示，模拟计算过程仅考虑充气过程，充气时长为8 h。

3.2 圆柱形洞室不同长度半径比值K对热力学特性影响

4种K值设计方案洞室充气8 h的内部气体温度均值T和压力p变化规律如图7、图8所示。由图可知，四种洞室内温度均值随充气时间增加而升高，其中上升速率最快的洞室为K=20 的狭长洞室，上升速率最小的洞室为K=5的洞室。气体温度均值在四种K值的洞室内有着较大的差异，在充气末时刻K=20 的狭长洞室气体温度均值比K=5 的洞室温度均值高35.8 K，温度均值随着K值的降低呈降低趋势，但不是K 值越小，温度均值越小，K=2.5 的洞室体温度均值比K=5 的洞室高1.5 K。洞室气体压力p 在充气过程中区别不大，充气8 h 时，K=20 的洞室内部气体压力比其余3个洞室高0.15 MPa。

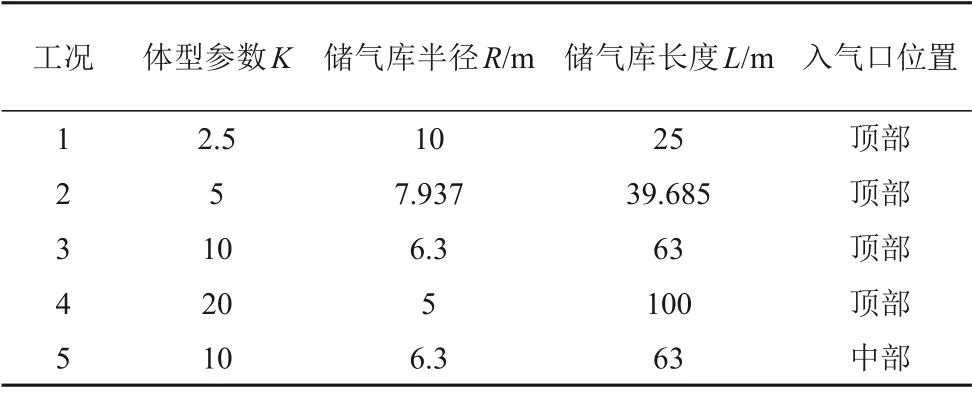
表2 四种设计方案下体型参数及初始条件Table 2 Shape parameters and initial condition under four design schemes caverns

图6 体型参数K=10时模型网格示意图Fig.6 Grid diagram of the model when the shape parameter K=10

不同K值洞室气体温度最大值的变化规律如图9 所示，K=20 和K=10 的洞室在充气过程中均会形成较高的最大温度，其中K=20 充气末时刻气体温度最大值为649.62 K；K=2.5 和K=5 的洞室气体温度最大值上升较缓，末时刻分别为378.19 K 和365.66 K，合理的选择K 值可以有效避免在充气过程中洞室内出现较高气体温度。充气过程中洞室存储的㶲值B随时间变化如图10所示，由图可知，不同K 值对于㶲值的存储影响不大，其中K=2.5、5、10 的洞室内存储的㶲值相同，只有K=20 时，㶲值较其余3个洞室高2.5×10-9J。

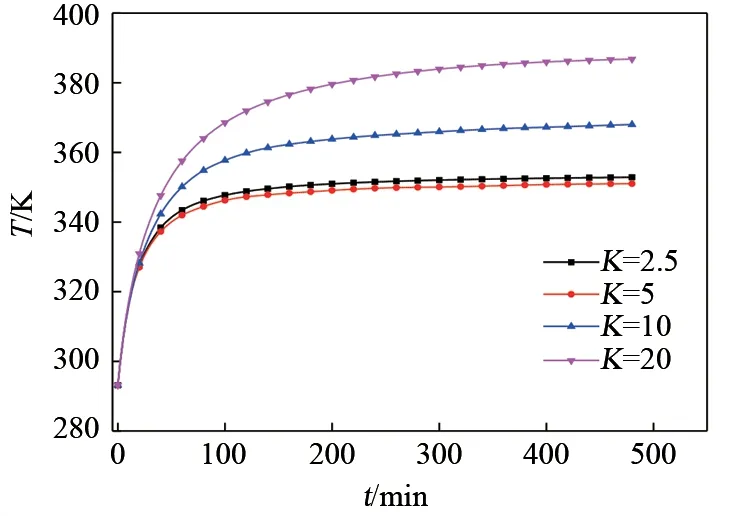
图7 不同K值洞室气体温度均值T变化规律Fig.7 Variation of average temperature T in the caverns with different K value

图8 不同K值洞室气体压力p变化规律Fig.8 Variation of average pressure p in the caverns with different K value

图9 不同K值洞室气体温度最大值Tmax变化规律Fig.9 Variation of maximum temperature Tmax in the caverns with different K value

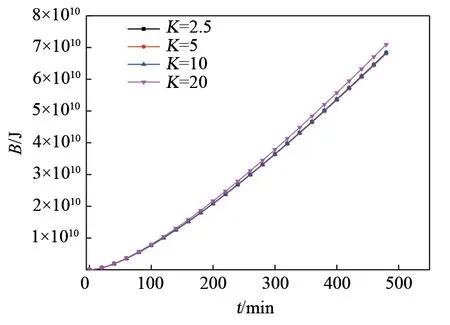
图10 不同K值洞室气体存储㶲变化规律Fig.10 Variation of exergy storage B in the caverns with different K value

不同K值的洞室在充气过程中，热力学特性影响较大的为温度，K值较大的洞室极易形成较高的气体温度，对于压力和存储的㶲值影响较小几乎可以忽略。较大的K值的洞室有较高的气体温度均值和最大值，但是不是K值越小，气体温度均值和最大值越小，当K值小到一定时，气体温度均值和最大值重新开始上升。

充气末时刻480 min 时刻4 种K 值洞室中截面的温度分布等值线如图11所示，对于K值较小的短粗型洞室，气体温度容易在入气口两侧的顶部聚积，形成高温区域；而K值较大的狭长型洞室，由于洞室较长，气体在底部进行压缩升温，所以洞室底部容易进行高温区域，且K值越大，洞室越窄越长，洞室底部的气体温度越高。

3.3 入气口布置位置对热力学特性影响

对K=10 设计方案的洞室分别采用顶部入气口布置和洞壁中部入气口布置，同样的边界条件和充气条件下模拟计算充气8 h 洞室内的热力学过程。两种入气方案的模型洞室气体温度均值和压力随时间变化规律分别如图12、图13 所示。顶部入气和中间入气其内部压力差异极小，可以忽略不计，最终时刻内部压力分别为3.79和3.81 MPa；而储气库内部体平均温度则在45 min后开始产生差距，且差距越来越大，顶部入气体平均温度最终为368 K，而中部入气体平均温度最终为352 K，表明中间入气可有效降低储气室内部温度均值，该参数下可降低温度均值16 K。

两种不同入气方式下的储气库内能量㶲B和焓H随时间的变化如图14、图15所示，焓H是温度的函数，由内部温度均值可知，顶部入气方式下的储气库内气体焓值较高，8 h末时为2.36×1010J，而中间入气的末时刻焓值为1.87×1010J。储气库内㶲值随时间呈曲线上升，两种充气方式下的焓值虽然不同，但是㶲值却相差不大，顶部入气下储气库内最终㶲值为6.84×1010J，而中间入气下储气库内最终㶲值为6.73×1010J。

图11 不同K值洞室中界面温度分布Fig.11 Contour of middle section temperature distribution in cavern with different K values

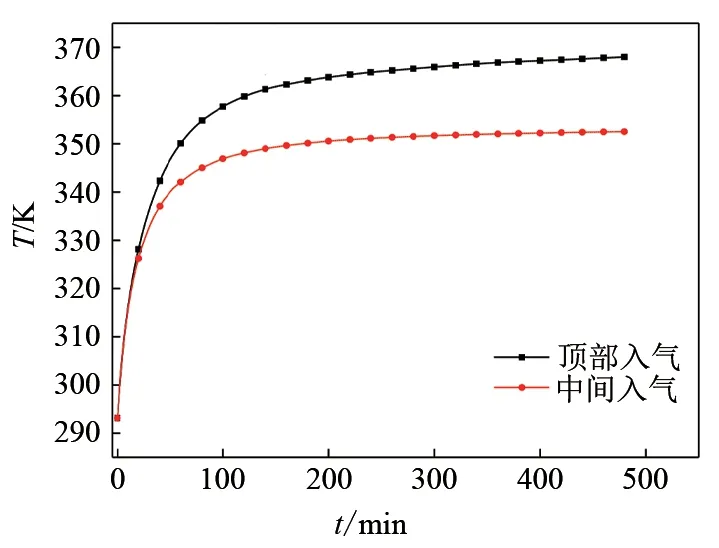
图12 不同入气口位置洞室气体温度均值变化规律Fig.12 Variation of average temperature in the cavern with different air inlet locations

图13 不同入气口位置洞室压力变化规律Fig.13 Variation of pressure in the cavern with different air inlet locations

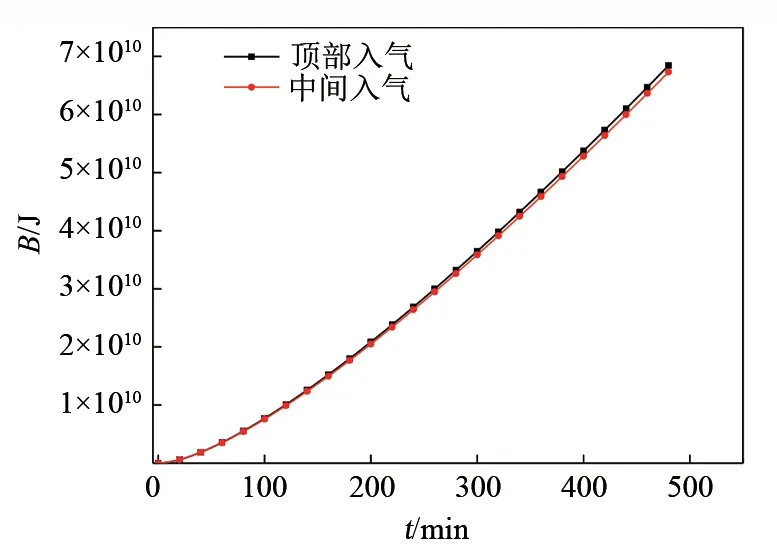
图14 不同入气口位置洞室存储㶲值随时间变化规律Fig.14 Variation of exergy storage in the cavern with different air inlet locations

图15 不同入气口位置洞室气体焓值随时间变化规律Fig.15 Variation of enthalpy in the cavern with different air inlet locations

充气过程中的洞室内气体温度最大值变化规律如图16 所示，由图可知，顶部入气的布置方式会使洞室内气体温度迅速上升，到220 min 时开始平缓，最终时刻温度最大值为528.87 K，中间入气的布置方式洞室内气体温度上升较缓，最终时刻温度最大值为369.26 K。储气库不同的入气口位置对充气过程中的压力影响不大，但是对于储气库内部的温度影响较大，内部温度最大值可降低159.61 K，中部入气可以避免最内部出现极高温度，这对于盐岩这类软岩储气库围岩稳定性有极大帮助。

对中间入气的洞室充气末时刻480 min 时中截面的温度分布等值线图进行绘制，结果如图16 所示，由图10 和图16 的对比可知，中部入气的洞室温度分布更为均匀，气体在从入气口注入，向上下流动压缩，温度在入气口一侧上下方累计，顶部入气会在底部形成高温区，中间入气可避免洞室内出现较高温度区，可有效避免洞壁出现较大的温度应力。

图16 不同入气口布置洞室温度最大值变化规律Fig.16 Variationofmaximumtemperatureinthecavernwith differentairinletlocations

图17 不同入气口布置洞室中截面温度分布等值线Fig.17 Contour of middle section temperature distribution in cavern with different air inlet

两种入气口布置方式对于洞室内充气过程的热力学特性影响主要体现在温度上，对于压力和㶲值存储几乎没有影响。顶部入气会产生较高的温度和较大的不均匀温度场，高温区域主要在洞室底部；中间入气方式温度均值较低，极大值也较顶部入气低199.5 K，洞室内温度场分布较均匀，对于盐岩这类性质较软、蠕变流变性较好的，较低的均匀温度场对于其稳定性和气密性是有利的，因此，在条件允许下，应当尽可能采用中间入气的充气方式。

3 结 论

（1）该数值方法可以较好地模拟CAES 电站运行过程中的洞室内热力学过程。在Huntorf 电站日循环运行过程中，洞室气体温度场存在不均匀性，变温层主要存在于洞壁附近，洞室内压力分布均匀。

（2）对于圆柱形洞室而言，设计方案中体型参数K 会显著影响洞室热力学过程。相同充气条件下，K值对洞室压力、存储㶲影响极小，但是会显著影响气体温度。K值越大，洞室内气体温度最大值和均值越大，但不是K 值越小，温度均值就越小，对一定的充气速率和充气温度下，存在最佳K值使得洞室气体温度场分布均匀，温度均值最小。K 值较大时，洞室内气体高温区域集中在洞室底部，而K值较小时的洞室高温区域集中在入气口一段的两侧。

（3）圆柱形洞室的入气口布置位置会显著影响洞室内气体温度分布，但不会影响气体压力和存储的㶲值。中间入气的布置方式会明显降低洞室内温度均值和最大值，分别可降低16 K和159.61 K。在洞室容积有限而充放气速率较快的情况下，应当尽可能采用K值为5、中部入气的设计方案。