基于特征处理与径向基神经网络的锂电池剩余容量估算方法

陈 峥，李磊磊，舒 星，沈世全，刘永刚，申江卫

（1昆明理工大学交通工程学院，云南 昆明650500；2重庆大学汽车工程学院，重庆400044）

锂电池因具有能量密度高、循环寿命长、成本价格低、环保污染小等优点而成为目前电动汽车动力电池的最佳选择[1]。在实际应用中，由于电池内部锂离子的活性会逐渐下降，导致锂电池的可用容量会在使用过程中有所损失，直接影响其剩余使用寿命(remaining useful life，RUL)。因此，为高效利用锂离子电池，有效估计当前锂电池的剩余可用容量，进而时时诊断其健康状态(state of health，SOH)是电池管理系统(battery management system，BMS)的重要功能[2]。

当前，研究人员已提出多种估算方法来获得可用容量，主要分为基于贝叶斯的方法、经验拟合的方法和数据驱动算法等。基于贝叶斯的方法包含卡尔曼滤波以及粒子滤波及其他相关改进算法。文献[3]采用双扩展卡尔曼滤波算法同时获得模型参数和当前电池状态，但此方法在电池循环寿命后期表现不佳。针对这一问题，文献[4]采用自适应无迹卡尔曼滤波算法，通过更新噪声协方差矩阵实现了SOH和RUL的多步预测，提高了电池全寿命周期内的估计精度。文献[5]采用无迹粒子滤波来估计锂电池的RUL，实际估算相对误差小于5%。以上基于贝叶斯的方法利用闭环滤波算法来估计电池健康状态的关键参数，对建模误差和测量误差具有较强的鲁棒性，但是建模过程复杂，实际估算过程计算量较大[6]。

在采用各种滤波算法之外，经验拟合的方法也被用于锂电池的状态估计领域[7]。文献[8]考虑锂离子电池的使用时间、充放电倍率和温度等条件，建立起广义电池寿命模型，实现对同一类电池健康状态的有效估计。文献[9]结合锂电池衰退后固态电解质界面层的生长和活性物质的损失情况建立电池老化模型，并采用递推最小二乘法估计模型参数，结果表明该方法所得结果相对误差小于1%。经验拟合的方法一般是在工程经验或电化学知识的基础上建立老化模型，精度较高，但是模型拟合需要大量的测试数据。并且，特定模型往往只能有效估计特定类型的电池或者特定老化情况下的电池状态，灵活性较差[6]。

如今，随着大数据和人工智能的快速发展，数据驱动的方法也被广泛应用于电池的状态估计[10]。文献[11]提出一种基于先验神经网络和马尔可夫链的SOH 估计方法，结果表明即使在不确定的外部条件下，该方法仍能够有效估算电池的内部状态。文献[12]采用具有自动相关确定结构的高斯过程回归算法(gaussian process regression，GPR)得到电池容量、温度和荷电状态(state of charge，SOC)之间的映射，实现对锂电池的多状态同时估计。文献[13]采用长短期记忆神经网络进一步优化GPR模型的结构，得到估算精度较高的估算模型。以上基于数据驱动的方法是一种黑箱模型，具有灵活智能的优点，但黑箱模型对训练数据集的好坏较敏感，较少的数据集会使模型得不到有效的训练，较多的数据集则有可能会导致模型复杂冗余，且可能造成模型的过拟合[14]。

为了解决采用数据驱动方法难以获得高效特征集的问题，本文基于特征处理与径向基函数(radial basis function, RBF)神经网络进行了锂电池剩余容量的估算，在保证精度的同时提高了估算效率。首先，采用局部离群因子方法对充电过程中提取的容量特征量进行优化处理，获得特征信息更集中的数据集，并对所获得的数据集进行特征选择，进一步降低数据的复杂度以提高估算效率，然后利用简洁高效的径向基神经网络建立剩余可用容量估计模型，并最终实现对锂离子电池剩余可用容量的快速准确估算。

1 锂电池循环老化实验

为研究动力锂电池衰退后可用容量随电池使用循环的变化情况，本文对两种规格的三元锂离子动力电池在室温条件下进行连续的恒流充放循环老化实验，操作流程见图1，电池相关信息如表1所示。实验采用美国Arbin 公司开发的BT-5HC-5V-100A电池测试系统进行。

容量衰退实验完成后共得到四组电池单体全寿命循环测试数据，分别标号为电池A-1、电池B-2、电池B-3、电池B-4，其中电池A-1 为A 型号锂电池，其它3 组为B 型号锂电池。以电池A-1 为例，某一循环的容量衰退实验电压与电流变化如图2所示，每个测试循环均由恒流充电、恒压充电、搁置、恒流放电、搁置等5部分组成，其中A型号恒流充电过程电流大小为2 A，B 型号为1.275A，A型号恒压充电过程截止电流为80 mA，B 型号为51 mA，A型号恒流放电过程电流为8 A，B型号为5.1 A。

图1 电池循环老化实验流程Fig.1 Battery cycle aging experiment process

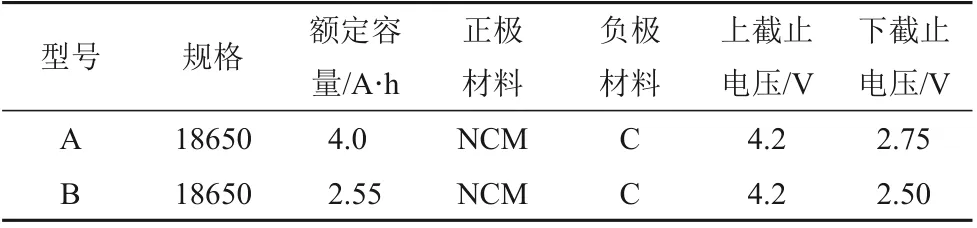
表1 测试电池基本参数Table 1 Test battery parameters

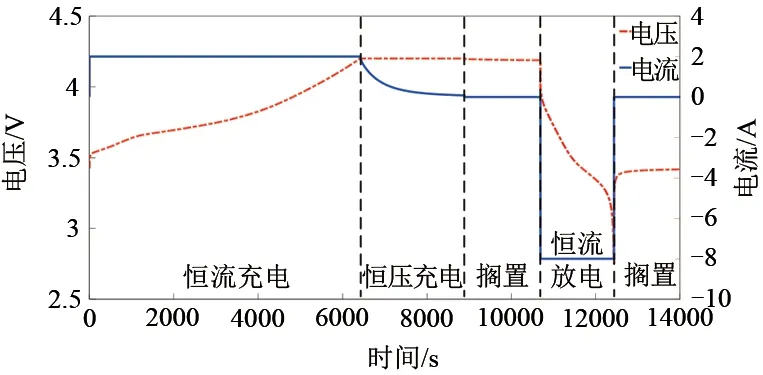
图2 循环测试过程电压与电流变化Fig.2 Voltage and current changes during cyclic testing

2 放电容量估算实现方案

2.1 容量衰退特征处理

2.1.1 特征量获取

在实际的应用过程中，考虑到锂电池的充电过程均为恒流恒压充电模式，对不同型号的电池具有一致性，而放电过程则因实际使用情况而存在差异，难以提取到稳定的特征量。因此，本文在充电阶段的实验数据中提取7组与锂电池剩余可用容量相关的特征量，并根据数据来源划分为两类。

第一类为根据传感器直接采集数据获得的特征量。分别将恒流充电阶段的充电时间CC-T、充电容量CC-C、恒压充电阶段的充电时间CV-T、充电容量CV-C 作为特征量。以电池A-1 为例，所提取的第一类特征量如图3所示。

第二类特征量为对传感器直接采集数据进一步挖掘所得到的特征量。其中，恒流充电阶段容量增量(incremental capacity，IC)曲线的峰值是有效表征锂电池内部理化特性的状态量[15]，IC曲线定义为容量与电压的微分，见式(1)

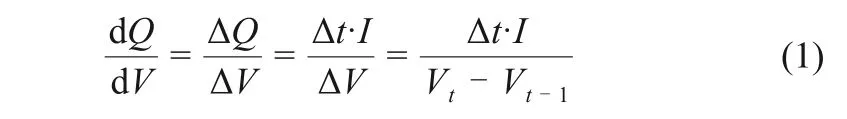
式中，Vt代表t时刻的电池端电压。在恒流充电模式下，电流为恒定值，当取极小的时间间隔Δt时，式(1)是成立的，由此可以快速绘制出IC曲线。绘制的IC曲线如图4所示，滤波后，可见曲线呈现明显的峰值特征。将每一循环IC曲线的最大值作为第二类特征量，称为：Max-IC。此外，分别取恒流阶段充电时间与对应循环恒压阶段充电时间的比值：CCT/CV-T和恒流阶段充电容量与对应循环恒压阶段充电容量的比值：CC-C/CV-C作为第二类相关特征量。电池A-1的第二类特征量如图5所示。

在实验数据的采集过程中，存在真实的电池特性数据与误差干扰数据掺杂混合的情况，在如图3、图5所示的两类特征量中，均存在有明显的数据离群点，而测试误差和电池自身衰退特性均会造成离群点的出现[16]。因此，本文采用局部异常因子算法消除测试误差对特征量规律性的影响，保留锂电池衰退过程中真实理化特性所反映出的特点，有效提高特征量所含信息量，进而提高模型学习效率。

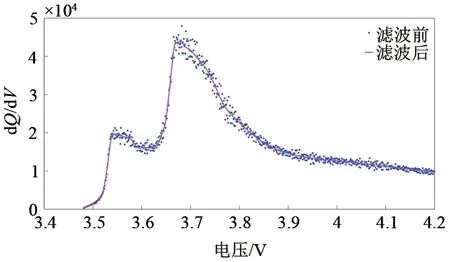
图4 IC曲线滤波前后Fig.4 IC curve filtering effect

图5 电池A-1的特征量Fig.5 Features of battery A-1

局部异常因子算法(local outlier factor，LOF)是通过计算每个样本的局部离群因子来判断其离群程度，是一种基于密度的离群点检测方法[17]。能够依据设定的阈值精准定位无效的离群点，避免了依据数据分布判别离群值的方法存在的误清洗有效数据的问题。特征量中采样点p邻域点的局部可达密度与点p 的局部可达密度之比的平均数就表示为点p的局部离群因子，见式(2)

图6 异常离群点的甄别结果Fig.6 Screening results of abnormal outliers

式中，NK(p)表示点p 的k 距离邻域，点o 为邻域内的某一点；lrdk(p)，lrdk(o)分别表示点p 与点o的局部可达密度。局部离群因子越接近1，说明点p 与其邻域点的周围密度相差无几，p 和邻域同属一簇的概率越高，反之，p 点可能是异常点。图6显示了应用局部离群因子甄别A 型号电池特征量CC-T 中异常离群点结果，原始数据中点1～5 均是明显可见的离群点，其中，点1 和点2 是由于测试环境所造成的异常值，需要进行平滑处理，而点3～5 处数值的变化是电池的可用容量回升现象在特征量CC-T 中的反映[16]，不能一并进行平滑处理，在特征选择的过程中应将其予以保留。

2.1.2 相关性检验

为验证特征量与可用容量之间是否具有密切的相关性，需要选用合适的方法对两者进行相关性检验。考虑到特征量与可用容量之间的关系是高度非线性的[18]，因此，需选用对特征数据分布没有要求的分析方法。

斯皮尔曼等级(spearman rank)相关系数又称为“等级差数法”，其取值在-1 到+1 之间，绝对值接近1 表明相关性越强。与其他积差相关系数相比，斯皮尔曼等级相关系数对于数据错误和极端值的反应不敏感，仅要求两个变量的观测值是成对的等级评定资料，或者是由连续变量观测资料转化得到的等级资料。不论两个变量的总体分布形态、样本容量的大小如何，斯皮尔曼等级相关系数均能够有效表征两者的相关程度[19]。

斯皮尔曼相关系数表示为式(3)

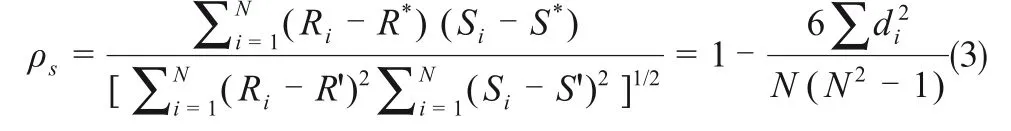
式中，Ri和Si分别是观测值i的取值等级；R*和S*分别是变量x 和y 的平均等级；di=Ri-Si表示两列成对变量的等差级数；N是观测值的总数量。

实验所得四组电池的循环放电容量与相应特征量之间的斯皮尔曼等级相关系数如表2所示，表中列出了经过异常离群点处理前后的相关性系数。结果显示，所提取的特征量与对应的剩余可用容量之间相关系数均在0.9左右，呈现出强相关性。且经LOF算法处理异常离群点之后，相关性系数均有提高，显著的增强了特征向量与对应循环容量之间的相关性。

表2 特征量与可用容量的Spearman等级相关系数Table 2 Spearman correlation coefficient of features and available capacity

2.1.3 特征降维

实际应用过程中，处理庞大的数据量会占用大量车载计算模块的计算能力，从而影响BMS 的整体性能。本文采用局部线性嵌入算法(locally linear embedding，LLE)对特征数据集进行降维处理，减少系统所需的存储空间，加快计算速度[20]。LLE属于流形学习的一种，在低维空间保持了原始高维空间样本邻域内的线性关系，能够较好的保持数据整体的几何结构和性质，适合应用于高度非线性数据的降维处理[21]。LLE算法对高维数据进行低维映射分为以下几步。

第一步：选取样本点的局部邻域点集P

对于给定的数据集X={x1,x2,…,xN}∈ℛD×N，xi∈ℛD×1，i=1,2,…,N，计算样本点的欧几里得距离，选取样本点xi邻域的k(k＜N)个近邻点xij，j=1,2,…,k。

第二步：计算线性重构的系数矩阵ω

如式(4)所示，定义均方差损失函数，求解样本点邻域的线性重构权重，构建局部重建权值矩阵。

第三步：通过得到的权值矩阵ω 得到样本集X的低维嵌入Y

将所有样本点映射到低维空间ℛd，即将D维的向量X 降维至d 维，每一个高维向量xi对应一个低维向量yi，Y={y1,y2,…,yN}∈ℛd×N的映射条件为最小化映射损失函数，见式(5)

对Y的求解等价于求解一定约束条件下的稀疏矩阵的特征向量，采用拉格朗日乘子法即可得到低维空间上的映射结果[22]。

2.2 基于RBF神经网络的容量估算模型构建

完成特征处理后，本文采用RBF神经网络开展了锂电池容量衰退模型的构建，RBF神经网络是一种在函数逼近、数据挖掘等应用场景下前馈神经网络[23]。其结构简洁，采用局部响应、局部逼近的原理训练网络，与全局响应的BP 神经网络等算法相比有收敛速度更快的优点，并且RBF神经网络的隐层神经元的激活函数是非线性函数，使得该网络可以逼近任意非线性函数。其结构由输入层、隐含层、输出层等三层构成一个多输入多输出的前馈神经网络，如图7所示。

数据由输入层节点传递到隐含层，隐含层节点一般由径向基函数构成，其中高斯径向基函数应用效果较好，而输出节点对隐含层的非线性运算结果进行线性运算为整个网络的最终结果。

图7 RBF神经网络结构模型Fig.7 RBF neural network structure model

隐含层节点中高斯径向基函数见式(6)

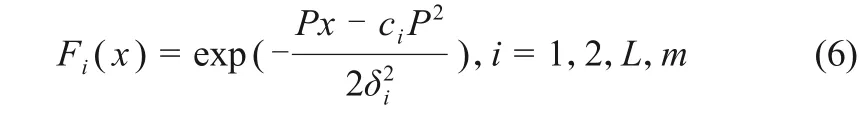
式中，x 为s 维输入向量；ci为第i 个径向基函数的中心；δi为第i个神经元感知范围，其决定该基函数的中心宽度；m为隐含层神经元的个数；||x-ci||表示x和ci之间的欧氏距离。Y为网络的输出向量。

输入层实现从x→Fi(x)的非线性映射，输出层实现从Fi(x)到Y的线性映射，即式(7)

式中，Wi为第i 个高斯径向基函数向输出层传递数据所附加的权值；W0为输出层的偏差项。

采用误差反向传播算法对网络内部参数进行确定，如图8所示，首先初始化权值矩阵并设定网络训练的目标误差函数及误差目标，之后将训练集输入网络循环更新权值矩阵，直至达到误差目标，完成网络训练，此时的权值矩阵以及各神经元径向基函数的参数为最终网络的结构参数。

图8 RBF神经网训练流程Fig.8 RBF neural network training process

图9 锂电池可用容量估算流程图Fig.9 Estimation flowchart of Li-ion battery usable capacity

锂电池剩余可用容量估计流程如图9所示，主要分为离线估算模型建立和在线容量估计两部分。在离线阶段，对测得的锂电池循环充放实验数据进行预处理，作为RBF神经网络的训练数据集。从充电阶段的时间、电压、电流、容量、IC曲线中提取出一系列特征向量，通过局部离群因子法剔除特征向量中异常离群点，消除环境噪声对特征量的干扰，并采用斯皮尔曼相关系数检验平滑后特征量与容量之间的相关性。利用局部线性嵌入法对多维特征量进行降维，减小数据的复杂程度，提高模型的训练效率。最后，训练RBF网络中的内部参数，确定容量估算模型。在线部分采用与离线阶段相同的方式对数据进行预处理之后作为模型输入，训练良好的估算模型输出高效准确的容量估计值。

3 估算结果与讨论

3.1 模型估算结果

3.1.1 不同训练量对结果的影响

为提高网络的学习速度及预测精度，将降维后的特征向量进行归一化处理之后作为RBF神经网络的输入值，模型输出为所估算的放电容量。在数据驱动方法的实现过程中，多采用60%数据用于训练模型，40%用于测试模型[7]。为评估所建立模型的有效性和鲁棒性，本文中，分别划分每组数据中的50%、60%、70%作为训练集，其余的作为测试集。输入网络模型后，不同训练量下模型的训练测试结果如图10 所示，分别采用均方误差(mean square error，MSE)、均方根误差(root mean square error，RMSE)、平均绝对误差(mean absolute error，MAE)对模型预测部分的效果进行分析，如表3所示。

图10 电池A-1、B-2、B-3和B-4训练测试结果Fig.10 Battery A-1，B-2，B-3 and B-4 training test results

表3 不同电池估算误差Table 3 Different battery estimation error

当60%的数据用来训练模型时，估计模型对四组实验电池的剩余可用容量输出了稳定有效的估算结果，测试区间的预测结果与实际采样数据非常接近。对比表3中的误差值，最大MAE出现在电池B-4的预测部分，仅为0.0494，MSE为0.0034，RMSE为0.0581，表明所建立的RBF神经网络估算模型对A、B两型号动力锂离子电池衰退后的容量均能做出较为精准的估算。

由图10中可以看到，当训练数据量增加至70%时，模型的预测精度有所提高，最大MAE 为0.0381，最大MSE为0.0022，最大RMSE为0.0472。当训练数据量减少至50%时，模型的估算精度只有略微降低，其中电池B-2 的预测误差较大，最大MAE为0.1067，最大MSE为0.0137，最大RMSE为0.1171，其他电池的预测精度与在60%训练数据下的预测结果相差无几。表明所提出的估算模型有良好的泛化能力和较强的鲁棒性，能够在数据有所波动的情况下有效估计不同类型电池的可用容量。

3.1.2 不同估算方法对比

为进一步验证基于特征处理所建立的RBF神经网络估算模型的在估算精度和效率上的优势，将Elman神经网络估算方法、BP神经网络估算方法和本文提出的估算模型分别应用于估计锂离子电池全寿命周期的容量衰退情况，容量估算结果、估算误差及消耗时间如图11、表4和表5所示。

图11(a)为三种不同模型对电池B-2的全寿命容量预测结果，所有模型的训练集均来自于电池B-3。图11(b)显示的是三种不同模型对电池B-3的全寿命容量预测结果，所有模型的训练集均来自于电池B-4。由预测结果可知，本文所提出的估算模型对电池B-2的容量预测结果相对误差除极少数据点在6%之外，其余均小于6%，且表征预测结果离散程度的RMSE仅为0.057，对电池B-3容量预测结果的相对误差则均在6%以内，显示出较高的估算精度。

图11 电池B-3预测电池B-2的结果(a)及电池B-4预测电池B-3的结果(b)Fig.11 (a)battery B-3 predicts the result of battery B-2,(b)battery B-4 predicts the result of battery B-3

表4 电池B-3预测电池B-2的估算误差及消耗时间Table 4 Battery B-3 predicts the estimation error and consumption time of battery B-2

表5 电池B-4预测电池B-3的估算误差及消耗时间Table 5 Battery B-4 predicts the estimation error and consumption time of battery B-3

与具有循环结构的Elman 神经网络和传统的BP神经网络相比较，Elman神经网络对电池B-2和电池B-3 的容量预测结果整体亦在6%左右，最大MAE 为0.0847，最大RMSE 为0.0874，BP 神经网络模型的预测结果中相对误差多数均大于6%，最大MAE 为0.0723，最大RMSE 为0.0869，而RBF神经网络模型对两电池容量预测结果的最大MAE为0.0612，最大RMSE 为0.0570，在预测精度和模型稳定方面均体现出良好的实际使用优势。

此外，由表4 可知，在相同的运算处理条件下，在预测电池B-2的容量时，RBF神经网络所消耗的时间仅为0.99 s，Elman 神经网络消耗时间为3.5 s，BP 神经网络表现最差，消耗时间为8.5 s。根据表5 可知，在预测电池B-3 的容量时，RBF 神经网络所消耗的时间为0.9 s，Elman神经网络消耗时间为3.5 s，BP 神经网络则高达9.4 s。对比三种预测模型，可以看出本文所提出的剩余可用容量估算方法所消耗的时间分别约为Elman 神经网络和BP 神经网络的1/5 和1/10，显示出较大的效率优势。

3.2 离群点处理对估算结果的影响

在容量估算的过程中，本文采用LOF算法对特征向量中异常离群点进行精确清洗。为体现不同异常值处理方法对模型估算结果的影响，对比了不处理离群点、应用Hampel 滤波器平滑离群点和应用LOF算法清洗异常值三种处理方式对预测结果的影响，如图12 和图13 所示。所预测的剩余可用容量为电池B-3 实验测得，电池A-1 和电池B-4 的实验数据为训练数据集。

结果显示，未经处理的特征量经LLE算法降维之后输入RBF模型，其容量预测结果精度较差，最大误差接近1 A·h，且结果分布较为分散，这说明不对异常值进行处理，神经网络模型不能有效学习到特征量与容量之间的映射关系，得不到理想的预测结果。经Hampel 滤波器平滑后的特征量在输入模型后对剩余可用容量估计的误差整体在0.2 A·h以内，但是，在电池循环寿命后期的估算效果较差。经LOF算法处理后的特征数据对应的容量估计误差则保持在0.2 A·h以内。

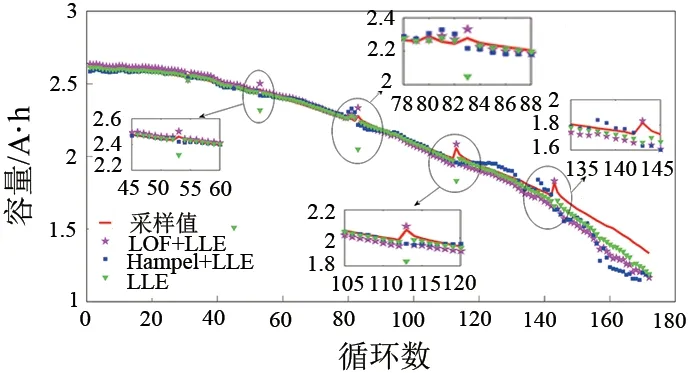
图12 不同异常值处理方式下容量估算结果Fig.12 Capacity estimation results under different methods

图13 容量估算结果误差Fig.13 Capacity estimation result error

在对出现容量回升现象循环的可用容量进行估算时，经Hampel 滤波器处理之后所对应的估算结果与经LOF算法处理后所得到的估算结果相比有较大差距，在第113实验循环，两者的容量估算绝对误差分别为0.0253 A·h和0.1003 A·h，在第143实验循环分别为0.0158 A·h 和0.1821 A·h。可见经LOF算法处理后的特征数据包含更细致的电池实际容量衰退信息，使估算模型能够更好的学习到锂电池容量衰退现象与特征量之间的关系，输出更为准确可靠的剩余可用容量值。

4 结 论

本文提出一种高效估算锂电池剩余可用容量的方法。由充电阶段的数据中提取7组与剩余容量相关特征向量，并采用LOF算法和LLE算法分别对多维特征量进行异常值精准甄别清洗和低维映射，提高特征值所含有效信息量的同时降低估算所需的计算需求，提升估算效率。在此基础上，利用RBF神经网络建立了容量估算模型。结果表明，该估算模型能够有效估算锂电池衰退后的剩余可用容量，与Elman神经网络模型和BP神经网络模型相比，在估算精度和估算效率方面均有较大优势。该方法能够实现对锂电池衰退后可用容量的高效、准确估算。