基于灰色关联分析联合VMD-SES-BP模型的滑坡位移预测

安 北，蒋亚楠,2，曾启菲

(1.成都理工大学地球科学学院，四川 成都 610059;2.成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059)

滑坡地质灾害在中国各个地区时有发生，具有高频性、突发性的特点，每年给国家和人民带来了不可估量的财产损失[1]，因此，积极开展滑坡预测预报研究工作对预防滑坡的产生，减少财产损失具有重要的实践意义。

目前，在滑坡位移的预测预报工作中，大多学者应用较多的预测模型有灰色模型(GM)[2]、人工神经网络模型(ANN)[3]，也有学者对GPS监测的滑坡位移时间序列采用不同的分解方法得到多个周期项、趋势项、随机项、噪声项序列，并根据不同序列的特点采用相应的机器学习算法或非线性拟合方法进行训练并预测，最后对应累加得到未来多期的滑坡位移预测值。刘艺梁等[4]利用经验模态分解(EMD)对非平稳的滑坡位移信号进行分解并结合BP神经网络进行预测，邓冬梅等[5]进一步提出了基于时间序列集合经验模态分解(EEMD)与机器学习算法结合的位移预测方法。机器学习预测模型中，最为典型的就是支持向量机(SVM)，同时粒子群算法(PSO)[5-6]、蚁群算法(ACO)[7]、差分进化算法(DE)[8]等也被引入SVM模型中以优化参数。此外李潇等[9]引入最小二乘法以转化SVM中二次规划问题并结合小波变换，证实了最小二乘支持向量机(LSSVM)预测滑坡变形的可靠性，Zhu等[10]在LSSVM基础上进一步考虑了降雨对滑坡的影响，取得了较高的预测精度。

以上的科研工作中均取得了一定的成果，但也存在一些不足：GM无学习过程，对非线性滑坡预测精度不高，ANN易出现局部收敛并过于依赖样本的情况。在累计滑坡位移时间序列的分解上，EMD分解方法得到的IMF分量个数未知，具有不可控性，若分解数量过少则考虑不够周全，分解数量过多则会增加预测模型的工作量，同样，受滑坡位移序列极其复杂的非线性特点，小波变换分解出的高频子序列往往过多，加大了预测的工作量。SVM模型中，核函数参数δ及误差惩罚因子C存在不确定性，需要进行人工设定。

本实验中，采用变分模态分解(VMD)对累计滑坡位移进行分解，相比于EMD方法，VMD分解出的低频分量更容易表达出信号波动趋势，且可以确定合理的模态分解个数。其自适应性特点可根据信号确定序列的模态分解个数，匹配各模态最优中心频率和有限带宽，从而实现各IMF分量的分离。对于低频分量，采用二阶指数平滑(SES)进行拟合，并逐期预测。而高频分量，通过灰色关联分析法对三峡地区滑坡的诱发因素进行分析，确定了模型的输入影响因子包含降雨量、库水位，与对应时间段的滑坡变形量作为BP神经网络的训练集进行学习并预测，最后叠加得到预测累计位移值。

1 模型建立

1.1 模型概述

通过灰色关联分析法分别将滑坡月累计降雨量，月平均库水位高度与该月滑坡变形量进行关联分析，证实了滑坡除受自身地质作用，如重力势能，岩层土质条件等影响外，区域降雨对滑坡的蠕动变形也具有较强影响作用，此外，针对于三峡地区一类涉水型滑坡，库水位高度的变化量也对滑坡变形存在一定的影响。通过对三峡地区某堆积层滑坡上安置的GPS监测器所测定的累计滑坡变形量数据进行变分模态分解，分解为多个IMF分量，对于低频分量，因为其逐渐稳定递增，可认为是滑坡变形的趋势分量，采用二阶指数平滑进行拟合，并对未来多期变化进行预测。对于高频分量，其存在一定的周期性变化规律，通过灰色关联分析对随机样本的实验，得出滑坡变形受每年周期性的降雨与库水位变化等外界因素的影响，通过相应的影响因子作为模型的输入量，在BP神经网络模型中进行学习和训练，最终得到短期的预测值。

1.2 变分模态分解原理

变分模态分解(VMD)最早由Dragomiretskiy[11]等人提出，是信号领域一种全新的自适应处理方法，该方法通过迭代搜寻变分模态的最优解，最终将信号分解与重构，得到若干IMF分量以及降噪信号。VMD对采样和噪声具有较强的鲁棒性，能够减弱模态混沌现象。该方法目前正逐步应用于地震信号去噪、图像处理等领域。

VMD将输入信号f分解为离散的模态uk，这些子信号再输入时具有特殊的稀疏性。因此每种模态可以选择其频谱域中的有限带宽作为稀疏性。假设每个子信号在中心频率ωk周围大部分是紧凑的，并随分解而确定，则为了评估信号的有限带宽，进行以下调整。

a)对于每个模态，通过希尔伯特变换得到相关的分析信号，以获得单边频谱。

b)对于每个模态解析得到的分析信号，通过与各自估计的中心频率的指数混合，将模式的频谱移至“基带”。

c)接着通过解调信号的H1高斯平滑度估算有限带宽，产生约束变分问题,见式(1):

(1)

d)式(1)中，K为分解模态个数，uk、ωk分别为分解后第k个模态分量和中心频率，δ(t)为狄拉克函数，*为卷积运算,见式(2):

L({uk},{ωk} ,λ)=

(2)

e)式(2)中，α为二次惩罚因子，用于降低高斯噪声的干扰，从而使uk与ωk得到优化，将优化的解引入ADMM算法中，并在适当的情况下直接在Parseval / Plancherel傅里叶变换中进行优化，来增强拉格朗日函数的鞍点，最终得到完整的变分模态算法，见式(3)—(5)：

(3)

(4)

(5)

f)式(5)中，γ为噪声容忍度，最后通过迭代满足式时，结束迭代，输出各个IMF分量，见式(6)：

(6)

1.3 二次指数平滑

二次指数平滑是基于一次指数平滑上进行的修正，去解决时序信号出现直线趋势时产生的滞后偏差等问题，利用该偏差规律建立趋势预测模型，计算如下。

(7)

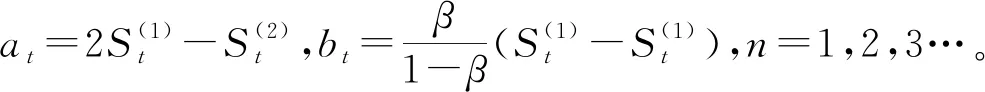
相较于传统的多项式拟合方法，二次指数平滑计算更简单，适应性也更强。

1.4 BP神经网络原理

BP神经网络是一种按照误差逆向传播训练的多层前馈神经网络，主要学习过程是信号的正向传播以及误差的反向传播[12-13]。其网络基本结构包含输入层、隐含层、输出层，见图1。

图1 BP神经网络原理示意

图中wmq表示输入层单元到隐含层的权重，θq表示隐含层中第q个节点的阈值，若q足够多则能够以任意精度去逼近期望值，q=1…i…q，wqL表示从隐含层到输出层权重。

正向传播，将信号x1…xj…xm作为 BP神经网络的输入值；从输入层经过各层权重wmq计算到达隐含层，在隐含层的激励函数φ(x)中进行处理得到hq，见式(8)。

netφq=w1q×x1+w2qx2+…+wmq×xm，

hq=φ(netφq+θq)

(8)

信号再从隐含层经过各层权重计算，将计算值代入激励函数φ(x)得到输出值yL：

netφL=w1L×h1+w2L×h2…+wqL×hq,

yL=φ(netφL+aL)

(9)

若输出值与理想值偏差较大，则计算出输出值与输入信号对应的期望值之间的误差值E：

(10)

为加快网络学习速度并提高数据精度，本实验的数据均进行了无量纲化。由此将月累计降雨量，滑坡变形量，月平均库水位变化量归一化处理为x1…xj…xm，将x1…xj…xm作为信号，通过训练拟合效果选择合适的激励函数φ(x)与φ(x)，得到预测的输出层yk。

2 工程实例

2.1 灰色关联分析

以三峡地区白水河滑坡为例，该滑坡位于长江南岸，滑坡体处于长江宽河谷地段，南高北低，呈阶梯状向长江展布。前缘抵长江，东西两侧以基岩山脊为界，总体坡度约30°，其后缘高程达410 m，以岩土分界处为界。其南北向长度约600 m，东西向宽度约710 m，滑体平均厚度约30 m，体积约1.26×107m3，为堆积层滑坡[14]。取该滑坡区域GPS监测器72期历史数据进行实验，每月1期，通过灰色关联分析法研究影响滑坡形变的影响因素。为保证分析样本的随机性和可靠性，随机选取12期滑坡的变形量与该期对应月累计降雨量，月平均库水位变化量，使用灰色关联分析法，比较各因素之间的发展趋势的相似程度。具体步骤如下。

a)确定影响系统行为特征的比较数列，其中影响目标序列的因素ai包括月平均库水位变化量，月累计降雨量，累计形变量，记作式(11)：

在我院档案管理工作中应用优秀计算机信息技术,实现信息全面交互,创建办公自动化大环境,提高自身工作效率。

(11)

其中,ai(m)为第i个对象的第m个影响因素。将库水位和变形量的数据以及降雨量和变形量的数据代入式(11)中，建立两组比较数列。

b)分析两组数据，建立相应的参考数列。确定反应系统特征的参考数列，以各指标的最优值构成参考数据列，见式(12)：

a0=(a0(1),…,a0(m))

(12)

c)数据初始化，因系统中各因素的物理意义不同，进行灰色关联度分析时，本实验采用初值化法进行无量纲化，见式(13)：

(13)

d)计算参考数列对应元素的差的绝对值，见式(14)：

Δ=|t0(k)-ti(k)|，i=1,2…,n;k=1,2…,m

(14)

e)计算关联系数，见式(15)

(15)

式(15)中，miniminkΔ表示查找每个对象，对应的影响因素的最小值；ρ为分辨系数，取值范围为0<ρ<1，其是为了减小由于Δ最大值的数值太大而造成的失真，提高关联系数之间的差异显著性[15]，本实验取ρ为0.5。

f)计算关联度，分别计算各个参考序列对应元素的关联系数的均值，见式(16)：

(16)

最终由式(16)得到每期滑坡变形量分别与当期月降雨量、月平均库水位变化量关联度，关联结果见表1、2。

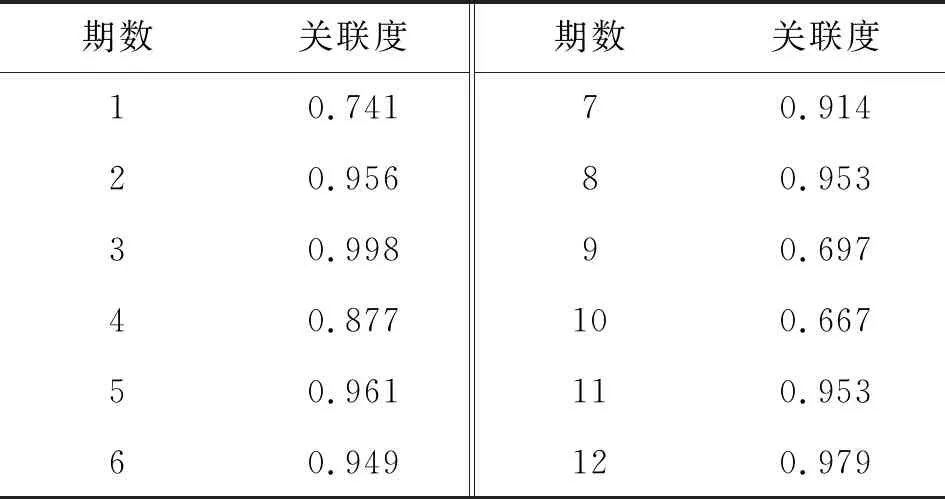
表1 滑坡变形量与库水位关联度

表2 滑坡变形量与降雨量关联度

若因素趋势曲线越相近，则其关联程度越强，关联度越强趋近于1，反之越弱越趋近于0。由12期的随机试验样本可见，滑坡变形量与库水位变化量的最大关联度为0.987，最小关联度为0.700，平均关联度为0.877。与累计月降雨量的最大关联度为0.995，最小关联度为0.667，平均关联度为0.899。可见，降雨和库水位的变化对滑坡的形变具有较强的关联作用，且库水位变化对滑坡形变的影响大于降雨对滑坡形变的影响。此外，降雨对滑坡的形变存在滞后效应，因此在使用BP神经网络对高频IMF分量学习训练时，需要加入两月累计降雨量作为新的影响因子。

2.2 滑坡位移分解与预测

a)根据试验步骤，首先进行滑坡变形的位移分解，通过变分模态分解法分解72期白水河滑坡累计位移变形数据，前60期作为训练学习样本，后12期作为预测对比样本。为避免产生多余的虚假分量，且保证分解出的IMF分量均有物理意义，通过试验最后确定分解模态数为K=3，惩罚参数C=0.5和上升步长τ=0.2。因而得到3个模态分量，结果见图 2。

a)原始位移

b)IMF1随机分量

c)IMF2周期分量

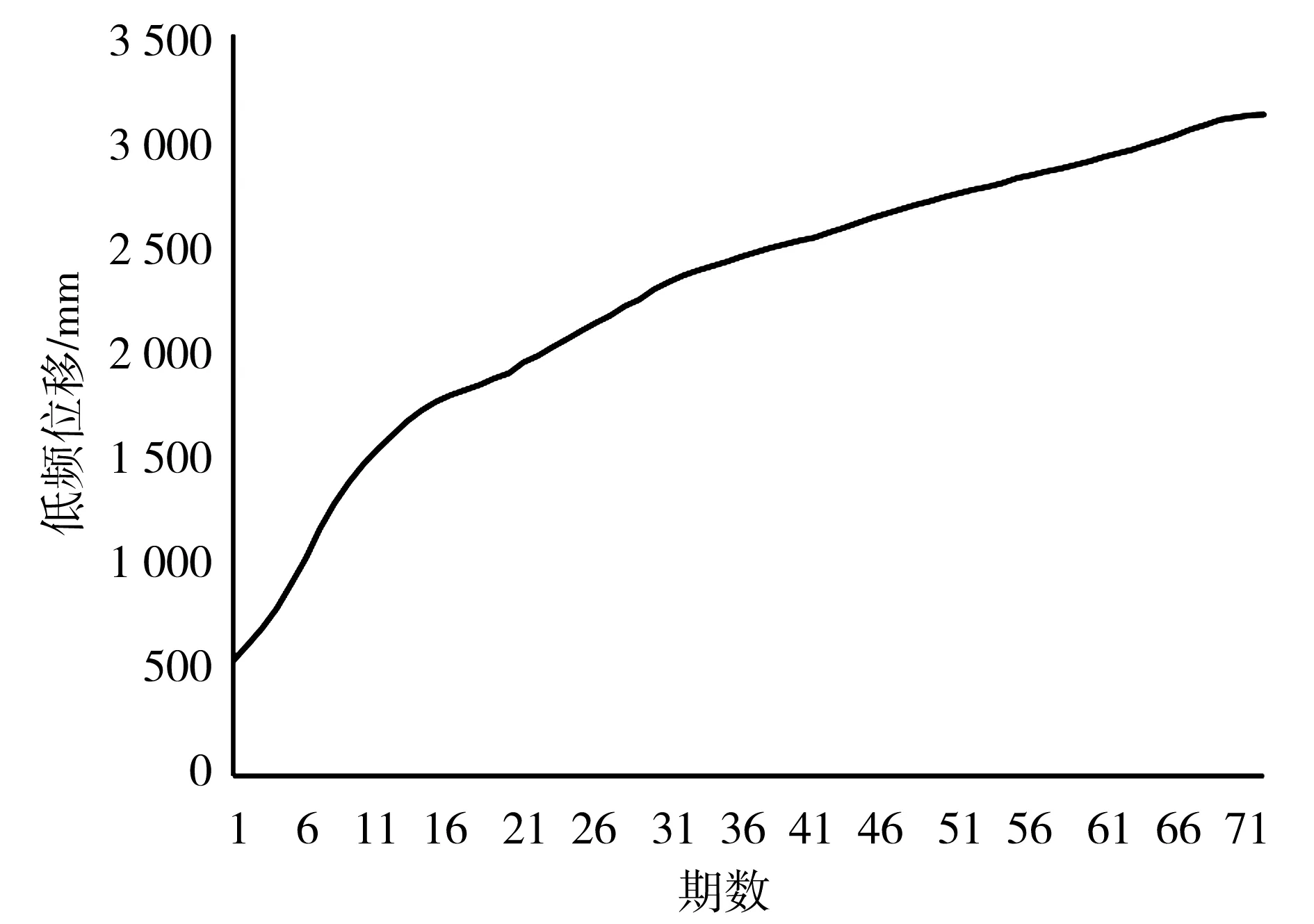
d)IMF3趋势分量

图2中， IMF1、IMF2分量为高频部分，代表了滑坡位移的随机噪声和周期部分，IMF3分量平稳递增，为滑坡位移的趋势部分。

b)对IMF1、IMF2分量通过BP神经网络进行学习并预测。根据2.1节中灰色关联分析，选用7个影响因子作为BP神经网络的输入值，分别为：前60期对应的月累计降雨量，两月累计降雨量，月平均库水位变化量以及每期滑坡变形量的前四期数据，因而输入节点数为7，输出节点数为1。隐含层传递函数设置为purelin，学习速率为0.01，通过实验设定隐含层数为3，学习结果见图3。通过拟合学习以后，根据对应影响因素得到后12期IMF1、IMF2分量的预测值。

c)对IMF3趋势分量的拟合由1.3节中二次指数平滑进行拟合，通过试验，选取β=0.15，可取得较好的拟合效果。根据式(7)最终得到后12期趋势分量预测值。

d)最终，将各自IMF分量的预测值对应相加得到滑坡位移预测值，并与真实值进行对比分析。

a)IMFI

b)IMF2

2.3 试验验证

为证实本模型的预测精度，采用均方根误差(RMSE)，平均相对百分误差(MAPE)，相关系数(R2)作为定量评估标准，见式(17)—(19)：

(17)

(18)

(19)

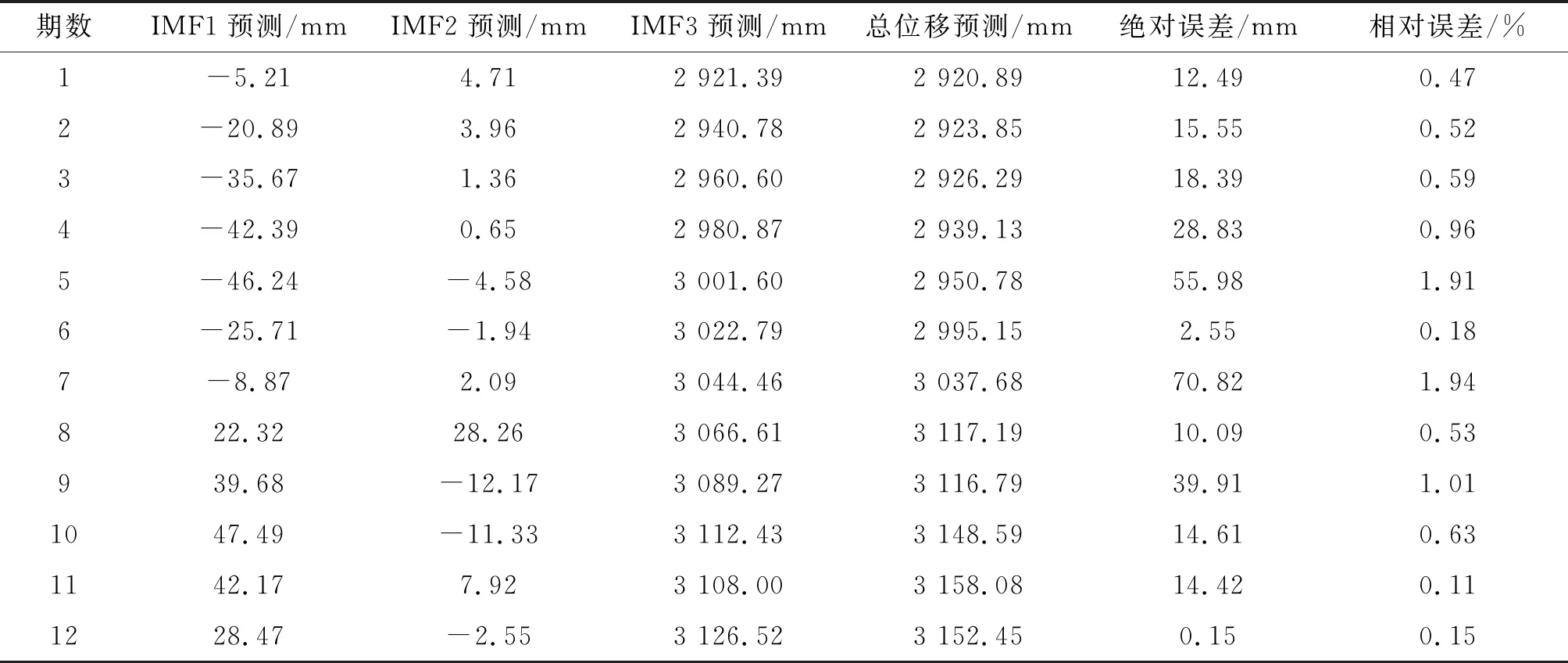
表3 试验数据对比

最终在本模型中，总位移均方根误差(RMSE)为3.14 cm，平均相对百分误差(MAPE)为0.78%，总位移相关系数(R2)为0.986，可见本模型预测精度较高，在滑坡位移预测方面具有一定的应用价值。

3 结论

本实验针对三峡地区“阶梯状”位移滑坡，提出了一种新的拟合预测模型：VMD-SES-BP模型。在模型中，将滑坡位移时间序列作为数字信号，通过变分模态分解将该信号分解为高频序列IMF1、 IMF2分量以及低频序列IMF3分量。通过灰色关联分析法，证实三峡地区的降雨和库水位的变化是滑坡演化过程中的主要触发因素。将历史监测的60期月累计降雨量、两月累计降雨量、月平均库水位变化量和前4期位移变形值共同作为BP神经网络的输入层，通过训练学习后得到后12期IMF1、IMF2分量预测值。同时采用二阶指数平滑对IMF3分量进行拟合并预测，最终将各分量预测值累加得到后12期滑坡位移预测值。通过精度分析，RMSE为3.14 cm，MAPE为0.78%，R2为0.986，证实了该模型针对三峡地区“阶梯状”滑坡位移预测上具有一定的应用价值。

此外，从实验的结果和趋势分析，此类“凸跃”位移的变化大部分集中在每年的7、8、9月份，在此期间，三峡地区的降雨量较大，增大了滑坡的重力势能，加剧了滑坡形变的产生。同时，受水流渗透进岩体的速率影响，三峡水库水位的下降或上涨使得地下水位与库水位形成正负落差，同样影响着滑坡形变量。因此，未来对三峡滑坡形变的预测预报中，应着重分析降雨和库水位的变化。