小波神经网络模型在滁河流域南京段洪水预报中的应用

朱永军，湛忠宇

(江苏省水文水资源勘测局南京分局，江苏 南京 210008)

小流域洪水预报是当前水文科学中亟待研究的一个方向[1]。中国小流域众多，洪水频发，一般具有历时短、突发性强等特点，洪水预报难度较大。特别是在梅雨季节，它经常会引发一系列地质灾害，例如泥石流和滑坡，也很可能破坏生态环境等。因此，研究如何提高小流域洪水预报的精度十分有意义。

国内外学者纷纷对小流域洪水预报进行分析探讨，基于物理意义的水文模型如新安江模型、SWAT模型、HEC-HMS模型等已广泛应用于各个小流域[2-5]，并取得了显著的成效。无需考虑物理过程的神经网络可搭建输入与输出的复杂关系，引起了水文预报研究者的极大关注。1986年Rumelhart等正式提出BP神经网络，1981年Jean Morlet建立了Morlet小波，1997年，李建平出版的《小波分析与信号处理——理论》，介绍并检验了小波分析的应用研究成果[6]，日益成熟的神经网络应用于各个领域[7-8]，获得了不错的效果。BP神经网络作为最常用的人工神经网络[9]，已在河道洪水预报、降水径流过程模拟中取得广泛的应用[10-11]。BP神经网络在收敛速度和适应性等方面仍有一定的提升空间，而小波神经网络有更强的适应性和泛化能力，往往预报精度更高，在水文水资源等领域得到了很好的发展[12-15]。滁河流域南京段承受上游过境洪水的同时又受下游江潮顶托，洪水聚集较快而河道排泄不通[16]，洪水预报精度偏低，本文通过新建小波神经网络和BP神经网络洪水预报模型，应用于滁河流域南京段研究区，以此来对比模型的适应性和预报的准确性，从而为研究区选择高效精准的洪水预报模型提供参考依据。

1 研究区概况

本文研究区滁河流域南京段位于江苏省南京市六合区，属于长江流域，区域面积约850 km2(图1)。区域内河线迂回曲折，河床狭窄，主要支流包括皂河和八百河等。研究区降雨时空分布不均，大泉水库站、马集站、六合站、金牛山水库站等记录了降雨数据，出口处红山窑闸站记录了流量数据。图1显示了研究区域及其河流系统和测站的分布情况。

图1 滁河流域南京段水系和测站分布

2 研究方法

小波神经网络(wavelet neural network，即WNN)既体现了小波分析理论，又融入了神经网络理论[6]。它的特点是以BP神经网络结构为模板，在信号正向传递和误差反向传递的循环过程中达到许可误差。小波神经网络三层之间各小波元互相关联，而每层各自小波元之间无关联。图2是小波神经网络结构示意。

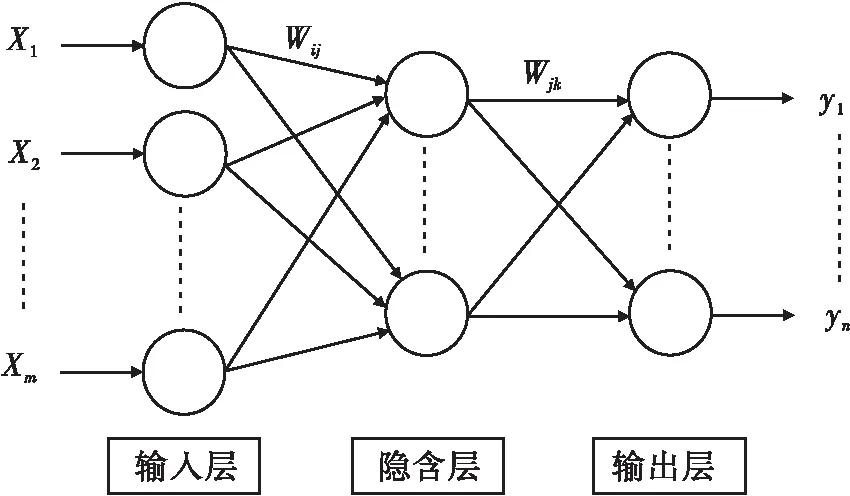
图2 小波神经网络结构示意

3 计算与分析

本文通过建立BP神经网络洪水预报模型和小波神经网络洪水预报模型，经过对比分析为滁河流域南京段提供高效精准的洪水预报模型。

3.1 选定样本数据

样本数据由输入数据与输出数据两部分组成。但在实践中小流域地区通常缺乏监控数据，例如暴雨、下垫面、温度、蒸发等，这些都是可能影响洪水形成的重要因素。本文在研究区域内获得了4个测站(大泉水库、马集、六合、金牛山水库)的2010—2019年长系列降雨资料，依据泰森多边形方法对4个站点雨量进行加权平均，得到小流域的面平均降雨系列，从中选定16场暴雨数据作为输入数据。本文同样获得了流域出口处红山窑闸站的2010—2018年长系列闸上水位数据，通过水位流量关系得到长系列流量数据，从中选定16场对应时刻的洪水数据作为输出数据。

本文共选取了16组样本(表1)，每组样本包括80个数值为输入数据、80个数值为输出数据，样本时段数为1 h。

表1 场次洪水基本信息

为了加快模型收敛速度、提高模型精度，在网络训练之前通过式(1)对样本数据进行归一化，利于模型训练的稳定性[7]。归一化可将表达式去掉量纲，从而使样本数据转换到0～1范围之内，变成纯量。

(1)

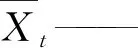
3.2 参数初始化

参数包括两部分，分别为小波神经网络参数和BP神经网络参数。小波神经网络的参数有伸缩因子a、平移因子b和权值wij、wjk，BP神经网络的参数有阈值和权值，这些参数都进行随机初始化。小波神经网络的隐含层激励函数为小波函数，而BP神经网络的可选用sigmoid函数。其余参数可设置一致，最大训练次数为1 000，目标误差为0.000 1，学习速率为0.01～0.50。

3.3 构建网络结构

本文随机选取8组样本数据进行网络训练，4组进行网络验证，4组进行网络测试。根据样本数据，显而易见输入层和输出层均有80个节点，而隐含层节点数可根据经验公式(2)、(3)，从小到大依次试凑。在MATLAB中运行代码，经过8组样本数据训练，模型自动对网络的参数进行优化调整，再经过4组样本数据验证，最终确定小波神经网络模型采用三层网络结构80-22-80，BP神经网络模型结构为80-36-80。

l

(2)

(3)

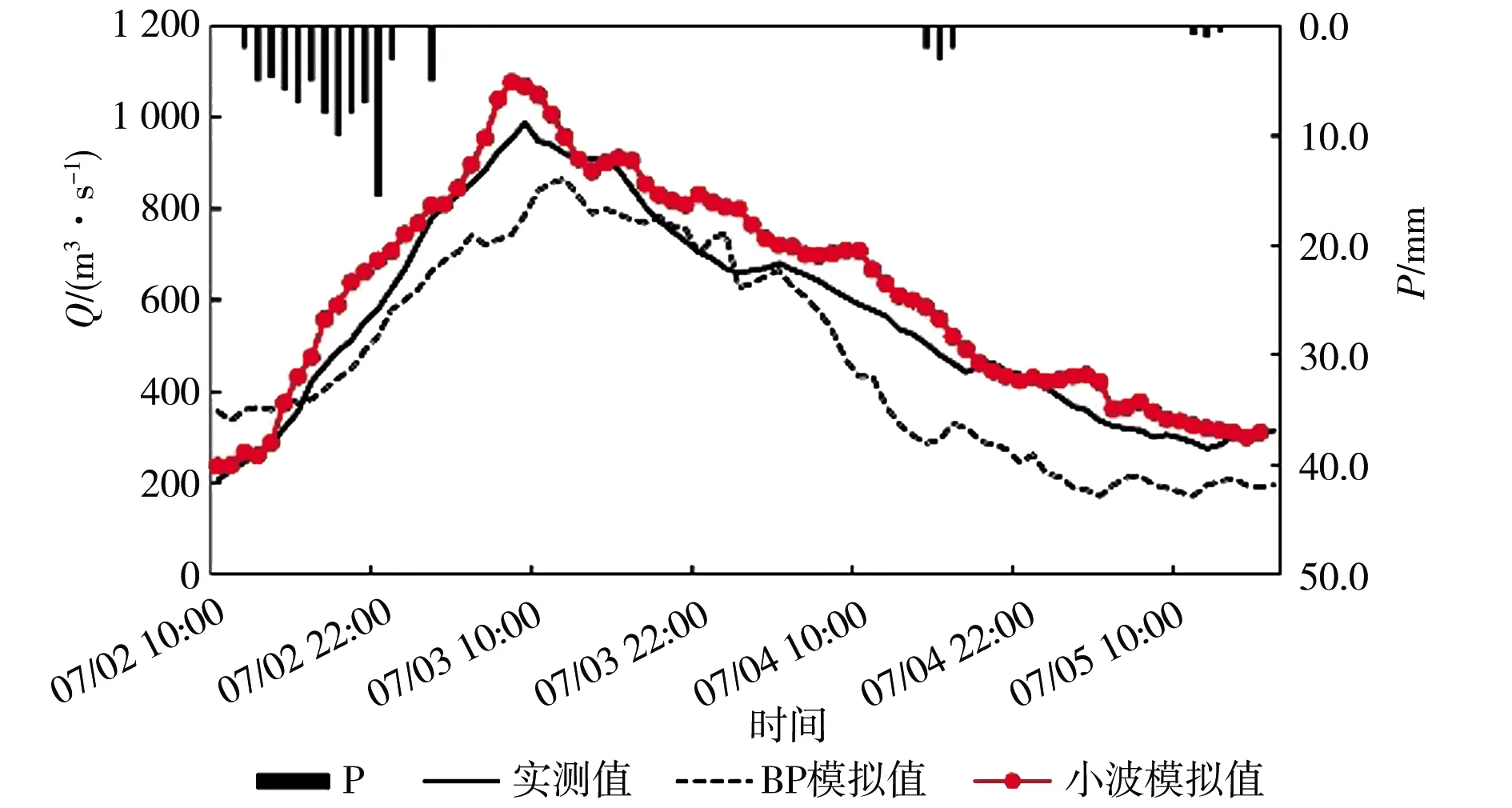
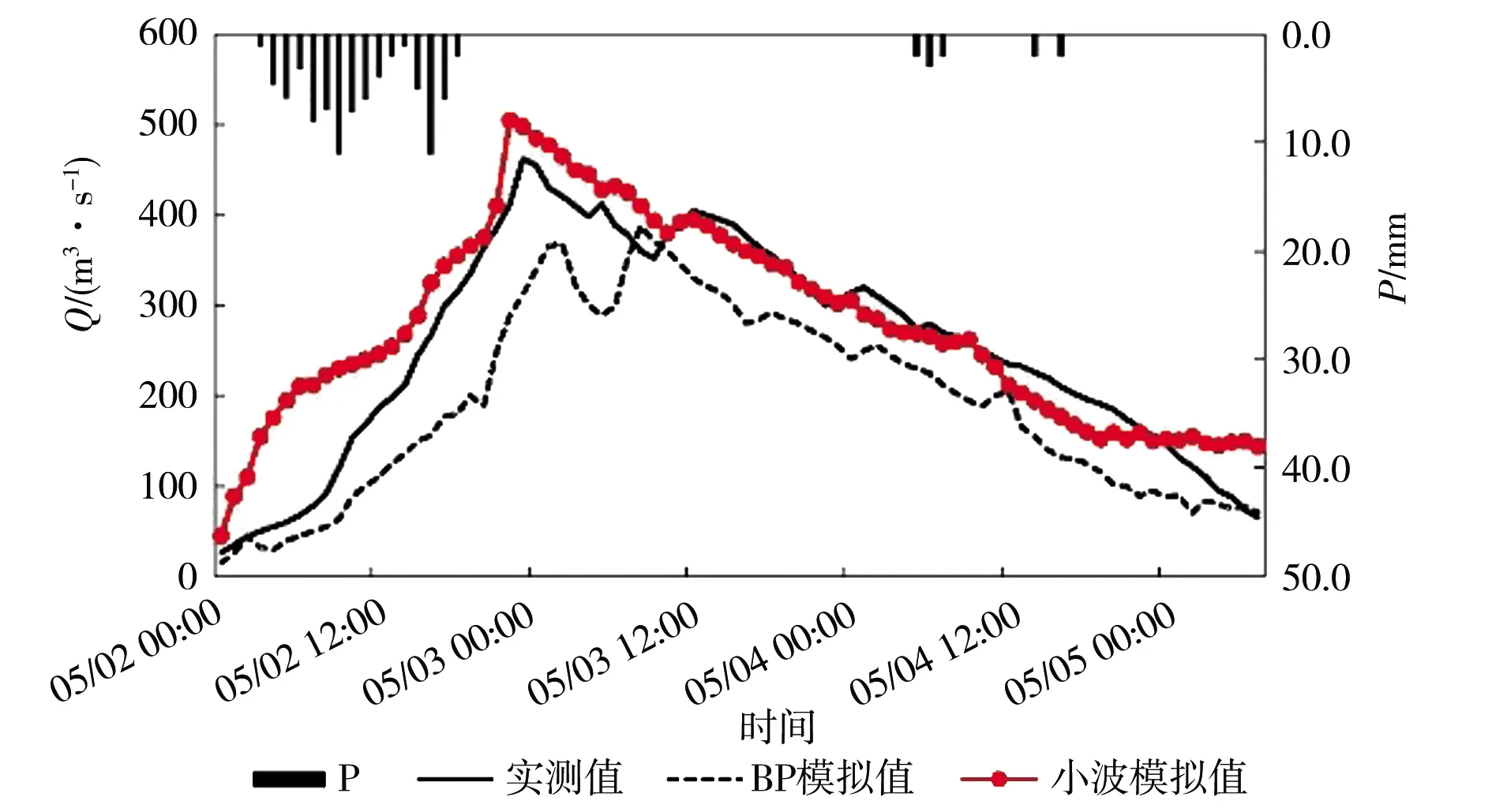
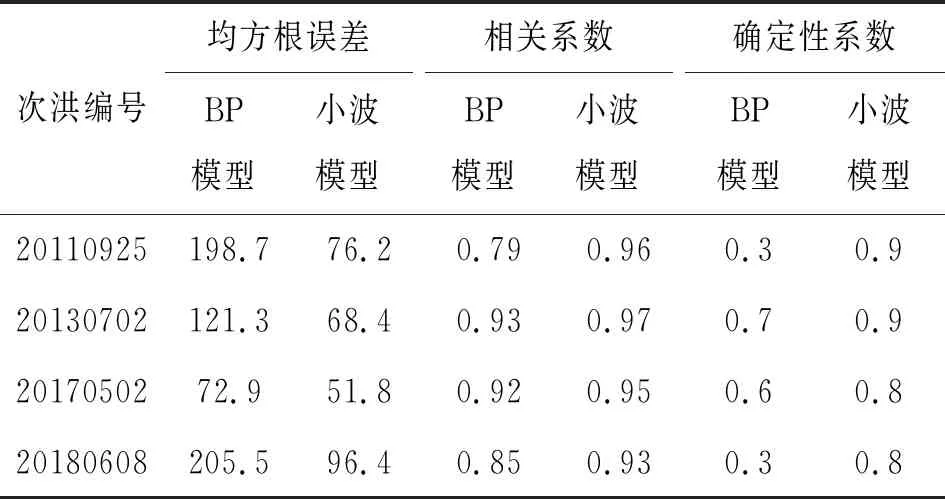
3.4 结果对比

本文利用剩余4组暴雨数据(20110925、20130702、20170502和20180608)分别进行BP神经网络模拟和小波神经网络模拟。模拟结果见图3，模拟结果见表2。

由图3可知，从定性来看小波神经网络模拟过程相较于BP神经网络模拟过程更贴合实测过程。从定量来看，一般根据GB/T 22482—2008《水文情报预报规范》(以下简称国标)规定，选用总流量相对误差、洪峰流量相对误差以及峰现时间相对误差等指标来评定洪水预报的精度。

a)20110925

b)20130702

c)20170502

d)20180608

由表2给出的3个评价指标表明：①洪峰流量相对误差，小波神经网络模拟20110925场次误差为8.8%，20130702场次误差为9.1%，20170502场次误差为9.3%，20180608场次误差为3.0%，均不超过10%，远远小于国标许可误差20%；但BP神经网络模拟误差较大，20110925场次误差为-10.4%，20130702场次误差为-12.3%，20170502场次误差为-16.0%，20180608场次误差为-15.6%，均超过10%，勉强满足国标许可误差。②总流量相对误差，小波神经网络模拟误差均控制在10%以内，20110925场次误差为4.9%，20130702场次误差为9.7%，20170502场次误差为9.5%，20180608场次误差为-1.1%，远远小于国标许可误差20%；BP神经网络模拟误差很大，20110925场次误差为-22.4%，20170502场次误差为-24.5%，均不满足国标许可要求，20130702场次误差为-15.5%，20180608场次误差为-19.0 %，勉强满足国标许可误差20%。③峰现时间相对误差，国标许可误差小于3 h，小波神经网络模拟在四场次中误差均控制在1 h以内，精度较高满足要求；但BP神经网络模拟误差较大，20110925场次误差为6 h，20130702场次误差为3 h，20170502场次误差为3 h，20180608场次误差为-3 h，结果均不满足国标许可误差。

为了得到更合理的结论，本文还采用了均方根误差、相关系数指标和确定性系数，来评估模型的适用性与可行性(表3)。均方根误差能显著体现模型的优劣，值越小模型准确性越高，预报值同模拟值离散程度越小。相关系数的绝对值越接近1，预报值和模拟值相关性越强，越靠近0，相关性越弱。

表2 4个场次BP、小波模型模拟结果对比

表3 BP模型和小波模型模拟指标对比

由表3给出的3个评价指标表明：①均方根误差，对于同一个模型，次洪总流量越大，则均方根误差相对越大，对于同一场次，小波模型模拟误差均小于BP模型模拟误差，平均误差降低了50%；②相关系数，小波模型相关系数均大于BP模型相关系数，且小波模型相关系数均大于0.90，认为有较强的相关性；③确定性系数，小波模型确定性系数均大于BP模型确定性系数，小波模型确定性系数均大于0.80，模型精度高，BP模型确定性系数变化幅度大，最低降到了0.3，模型相对不稳定精度较低。总体来说，小波神经网络模型较BP神经网络模型适应性更强，模拟精度上有了较大的提升。

4 结论

a)本文根据滁河流域南京段洪水预报难、预报精度偏低等实际问题，分别新建了BP神经网络洪水预报模型和小波神经网络洪水预报模型。通过对比总流量相对误差、洪峰流量相对误差、峰现时间相对误差、均方根误差、相关系数、确定性系数等6个指标，表明了小波神经网络模型较BP神经网络模型更贴合实际洪水过程，预报精度更高、适应性更强，将来可为南京市六合区的防洪减灾决策提供科学的参考依据，从而更大力度地减轻强降雨对研究区造成的破坏和经济损失。

b)小波神经网络模型总体表现优秀，但仍有一定的改进空间，如若从优化参数、预处理样本数据、探索多因素对洪水影响等角度深入研究洪水预报，那么小波神经网络将成为最具前景的洪水预报实战手段之一。

c)小波神经网络模型耦合小波分析与神经网络，具有结构更简单、收敛速度更快、精度更高等优点。不仅可以应用于长系列小时洪水预测，还可应用至长序列日洪水预测、枯季径流中长期预测等，更可以将应用范围拓宽到各行各业实际预测中，如停车位预测、交通流量预测、股票波动预测等，解决城市生活中诸多预测问题，研究意义十分重大。