涂层表面形貌的分形表征研究

王洪娇，秦襄培

涂层表面形貌的分形表征研究

王洪娇，秦襄培*

（武汉工程大学 机电工程学院，湖北 武汉 430205）

涂层表面粗糙度值较小，用于表征涂层表面形貌特征时受仪器分辨率以及采样区域的影响较大。本研究利用AE-100白光干涉仪分别采集四组实验中TiN涂层以及钌铱涂层的表面图像、三维粗糙度参数S及表面三维形貌。基于分形理论采用与尺度无关的分形维数表征涂层表面形貌特征，采用盒子维方法利用MATLAB编程计算了涂层表面的三维分形维数。实验结果显示，与分形维数相比，粗糙度S的变化较大。因此，体现了分形维数在表征涂层表面三维形貌方面的优势。

涂层；表面形貌；盒子维方法；MATLAB；分形维数

表面工程技术应用在诸如航空工业、机械制造、生物工程、新材料、电子信息和新能源等多个领域，可以利用薄膜涂层材料的表面特性及其功能特性来发挥相应的作用[1-3]。目前，对涂层的研究大多集中于涂层制备方法、沉积温度、涂层结合力、耐磨性能等方面的研究[4-6]，极少见涂层表面形貌特征的研究，特别是将分形理论运用于涂层表面形貌方面的研究。本文以TiN涂层以及钌铱涂层为实验研究对象，采集涂层表面图像、三维粗糙度参数及表面三维形貌，利用盒子维方法通过MATLAB编程对涂层表面的三维分形维数进行了计算及分析。

针对三维表面测量的方式分为接触式的探针测量法与非接触式的光学测量方法两种，前者包含扫描探针显微技术及的机械探针测量法，后者的绝大多数则是基于光学技术实现的无接触、高精度测量[7]，光学探针式测量法和显微干涉法都属于非接触式测量法[7]。本文采用非接触式测量法。

1 实验条件

1.1 实验仪器

采用白光干涉仪（图1、表1）采集表面三维形貌，其中，AE-100设备及软件部分为此测量系统的主要组成部分，软件部分由采集部分及分析部分组成，采集部分可以得到实验的干涉图像及高度数据；分析部分则可以计算粗糙度、还可以生成3D图像。白光干涉仪的实验流程如图2所示。

图1 白光干涉仪

白光干涉仪实现了对实验试样表面的非接触式、高分辨率测量。在工作时，通过白光向方向扫描表面，得到高分辨率的图像，并实现高度测量；并且还可以得到表面相关的颜色信息。测量时，每个试样表面均采集3次形貌，测量的视野范围为928 μm×696 μm。

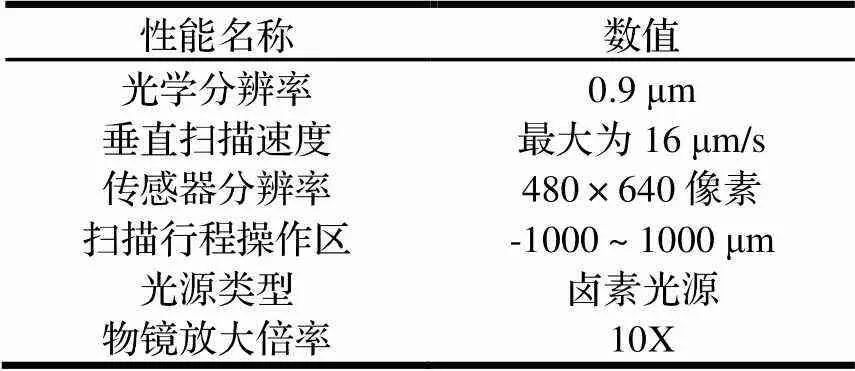
表1 AE-100白光干涉仪部分参数

图2 白光干涉仪的实验流程

1.2 实验试样

实验对象为TiN涂层试样与钌铱涂层试样，试样的主要参数如表2所示。

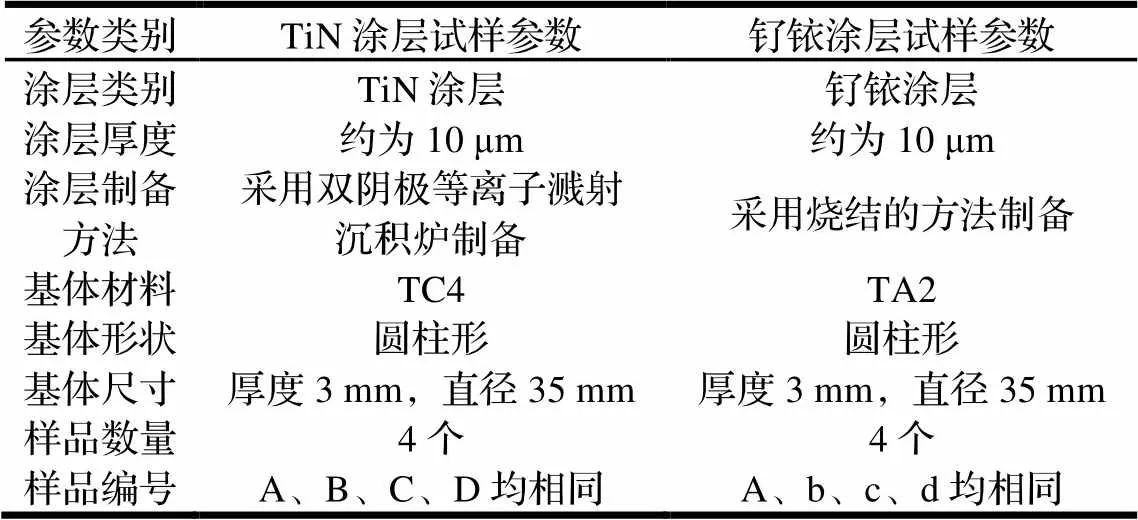
表2 试样参数

每组实验包含1个TiN涂层试样与1个钌铱涂层试样，分别称为第一组、第二组、第三组、第四组，如表3所示。

表3 试样分组编号

2 盒维法计算表面形貌的分形维数

由于盒计数法具有应用范围广、物理意义明确、计算精度较高且计算数量较小的特点，所以采用盒维数算法在MATLAB[8]环境中进行编程计算，对白光干涉仪测量的表面形貌进行分形维数计算。

选定盒子维法对表面图像进行分形维数的计算，根据测度维数的定义，则集合的分形维数可以定义为：

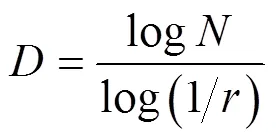
式中：为用“尺子”量度时的量度结果。

尺子度量的变化，则会导致结果变化，由此可计算得到分形维数。

比如图像的尺寸为×，假设其被尺寸为××的网格所覆盖，且＝×/，为整个图像的灰度级数，u和b之间包含至少一个灰度级数的网格个数，记为，那么则会随着取不同的值而变化，尺子＝/，是一常数，测量图像灰度级数的尺度为网格尺寸。那么，所采集图像的分形维数就可以由与的关系计算得到[9]。

对式（1）数学推理可以得到：

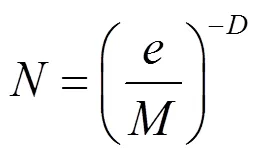
即：

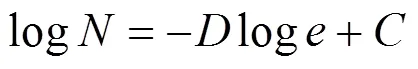
式中：为图像的分形维数；＝log为常数，通过不同的值可以得到对应的值[9]。

将、作出双对数图，通过MATLAB软件最小二乘拟合函数求出拟合直线，所得直线的斜率取正即为所求的分形维数。

3 实验结果

使用白光干涉仪依次采集每组实验中涂层试样的表面形貌及其三维粗糙度参数S，并计算其对应的分形维数。

3.1 TiN涂层表面粗糙度采集及表面分形维数计算

使用白光干涉仪采集得到四组实验中TiN涂层表面图像如图3所示、表面三维形貌如图4所示、三维粗糙度参数S分别为1.9876 μm、1.8866 μm、1.9651 μm、1.6939 μm。

图3 TiN涂层表面图像

图4 TiN涂层表面三维形貌

将四组实验中TiN涂层试样的表面粗糙度与将白光干涉仪采集到的涂层表面图像采用盒维法计算得到涂层表面形貌的分形维数数据整理列表，如表4所示。

3.2 钌铱涂层表面粗糙度采集及表面分形维数计算

使用白光干涉仪采集得到四组实验中钌铱涂层表面图像如图5所示、表面三维形貌如图6所示、三维粗糙度参数S分别为0.9452 μm、0.8424 μm、0.9816 μm、0.7277 μm。

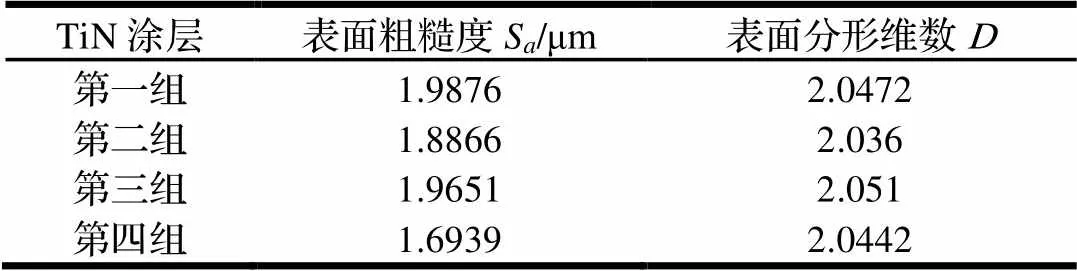
表4 TiN涂层试样的表面粗糙度与表面分形维数

图5 钌铱涂层表面图像

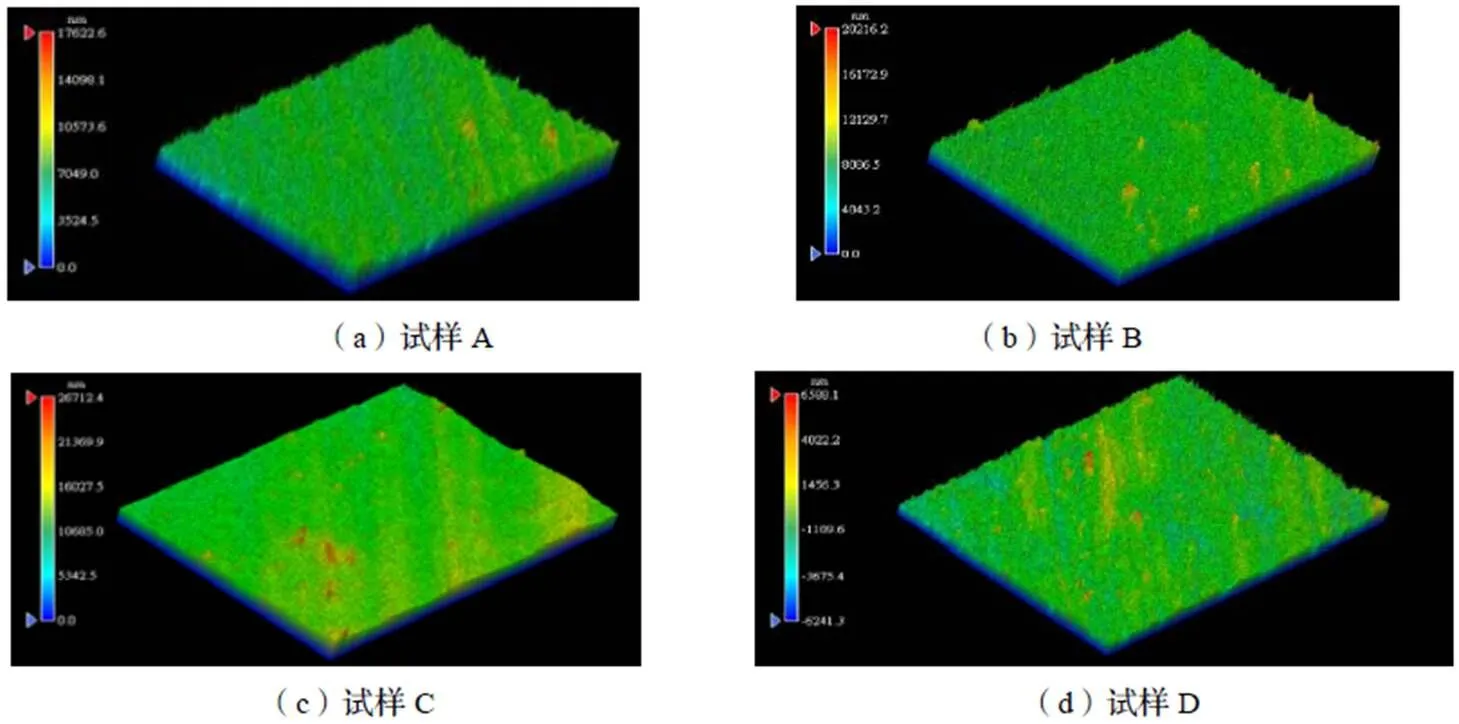
图6 钌铱涂层表面三维形貌

将四组实验中钌铱涂层试样的表面粗糙度与将白光干涉仪采集到的钌铱涂层表面图像采用盒维法计算得到涂层表面形貌的分形维数数据整理列表，如表5所示。

表5 钌铱涂层试样的表面粗糙度与表面分形维数

3.3 对比同种涂层的表面粗糙度与表面分形维数

为了进一步比较同种涂层四组实验的表面粗糙度与分形维数，将同种涂层四组实验中涂层表面粗糙度参数S及分形维数进行整理，绘制折线图如图7、图8所示。

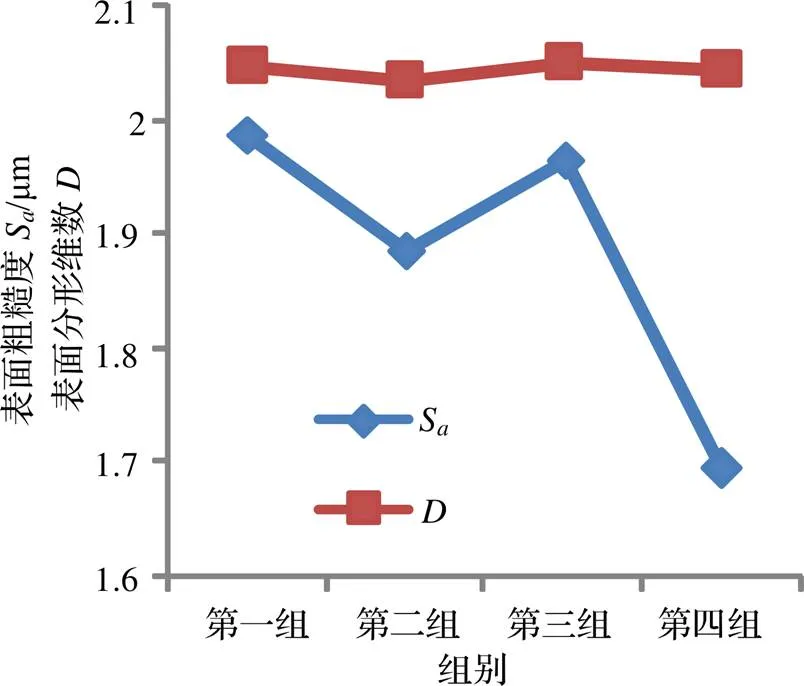
图7 TiN涂层表面粗糙度与分形维数对比

图8 钌铱涂层表面粗糙度与分形维对比

为使得出实验结果具有可比性，计算方差2及标准差，如下：

TiN涂层、钌铱涂层的试样表面粗糙度与分形维数数据的方差2及标准差计算结果如表6、表7所示。可以看出，与分形维数相比，粗糙度S的变化程度较大； TiN涂层和钌铱涂层的表面粗糙度四组数据的标准差均大于分形维数四组数据的标准差；与分形维数相比，粗糙度S的离散程度更高、误差也更大。

表6 TiN涂层试样四组表面粗糙度与分形维数数据的方差及标准差

4 结论

基于分形理论的盒子维法及涂层表面形貌图，可以利用MATLAB编程计算与尺度无关的分形维数对涂层表面形貌特征进行表征。

同尺度相关的表征表面形貌特征的表面粗糙度测量值较分散，而与尺度无关的分形维数的计算值则较稳定。

综合分析得，因为涂层表面粗糙度值较小，受仪器分辨率的影响，每次测量时显示的数值变化较大，并且选择试样表面不同的区域也会对结果造成影响。而分形维数是独立的，它不受仪器分辨率的影响。这体现了分形维数在表征涂层表面三维形貌方面的优势。

[1]C.莱茵斯，M.皮尔斯. 钛与钛合金[M]. 北京：化学工业出版社，2006.

[2]苏鸿英. 钛的工业应用前景[J]. 中国有色金属，2009（4）：74.

[3]胡清熊. 钛的应用及前景展望[J]. 钛工业进展，2003（Z1）：11-15.

[4]司莹. Mi60涂层织构图案制备与疲劳性能研究[D]. 西安：西安理工大学，2019.

[5]吴易谦，韦春贝，代明江，等. 沉积温度对NiCrAlY/Ag复合薄膜结构及性能的影响[J]. 表面技术，2019，48（12）：211-217.

[6]贵宾华，周晖，郑军，等. 偏压对MPP制备AlTiSiN纳米复合涂层结构及性能的影响[J]. 表面技术，2020，49（1）：228-236，275.

[7]郑毅. 垂直扫描白光干涉表面形貌测量软件系统研究[D]. 武汉：华中科技大学，2015.

[8]秦襄培，郑贤中. MATLAB图像处理宝典[Ｍ]. 北京：电子工业出版社，2011：440-460.

[9]蒋书文，姜斌，李燕，等. 磨损表面形貌的三维分形维数计算[J]. 摩擦学学报，2003（6）：533-536.

Fractal Characterization of Coating Surface Morphology

WANG Hongjiao，QIN Xiangpei

(School of Mechanical and Electrical Engineering, Wuhan Institute of Technology, Wuhan430205, China )

The roughness value of the coating surface is small, which is greatly affected by the resolution of the instrument and the sampling area. In this study, AE-100 white light interferometer was used to collect the surface image, three-dimensional roughness parameterSand three-dimensional surface morphology of TiN coating and ruthenium iridium coating in four groups of experiments. Based on the fractal theory, the fractal dimension independent of scale is used to characterize the morphology of the coating surface, and the box dimension method is used to calculate the three-dimensional fractal dimension of the coating surface by MATLAB programming. The experimental results show that the roughnessSchanges greatly compared with the fractal dimension. Therefore, the advantages of fractal dimension in characterizing the three-dimensional morphology of the coating surface are demonstrated.

coating；surface morphology；box dimension method；MATLAB；fractal dimension

TG335.86

A

10.3969/j.issn.1006-0316.2020.11.011

1006－0316 (2020) 11－0071－05

2020－03－16

王洪娇（1994－），女，山西武乡人，硕士研究生，主要研究方向为摩擦学计算机仿真。*通讯作者：秦襄培（1972－），男，湖北武汉人，博士，副教授、硕士研究生导师，主要研究方向为摩檫学计算机仿真、图像处理，E-mail：alexqxp@qq.com。