某航空发动机主轴轴承参数优化设计

范红伟，艾青牧，李家新，曾昭阳，刘森

某航空发动机主轴轴承参数优化设计

范红伟1，艾青牧2，李家新1，曾昭阳1，刘森3

（1.哈尔滨工业大学 机电工程学院，黑龙江 哈尔滨 150001； 2.哈尔滨工业大学 航天学院，黑龙江 哈尔滨 150001； 3.中国航发哈尔滨轴承有限公司，黑龙江 哈尔滨 150027）

随着轴承寿命研究的深入，有必要对轴承性能影响因素进行划分，使之更加具体化、公式化。为提高轴承的高可靠性并优化轴承设计参数，应用响应曲面（Box-Behnken）试验设计方法，利用Cobra软件模拟仿真分析了内沟曲率系数、外沟曲率系数和径向游隙对轴承性能的影响。选取内沟曲率系数、外沟曲率系数和径向游隙为自变量，以功效系数法确定统一函数为响应值，获得了自变量与响应值间的数学回归模型，能较准确地优化出统一函数的确定值。结果表明：内沟曲率系数和外沟曲率系数对轴承性能影响最显著，径向游隙影响不显著。最优参数组合为内沟曲率系数0.515、外沟曲率系数0.515、径向游隙0.14 mm时，统一函数值为0.645、轴承寿命为1.04×106h、外圈应力为965.683 MPa、内圈应力为964.527 MPa。

参数优化；沟曲率系数；高可靠性

轴承是航空发动机系统的重要核心部件，也是机械设备中不可或缺的核心部件，因此受到了国内外越来越多学者的关注。对于高速滚动轴承，主要集中应用领域为高端装备，如航空航天、高速列车、高精密机床等[1-3]。轴承使用性能直接影响发动机的寿命和可靠性[4-5]，因此对轴承性能的研究显得尤为重要，很多学者对此开展了大量的工作。

金燕[6]运用人工神经网络法完成热弹流润滑效应下航空滚动轴承疲劳可靠性分析。吕凤鹏[7]利用遗传算法对RV减速器转臂轴承进行了优化设计，选择从几何、强度和润滑等方面进行约束，完成了优化灵敏度分析。Jun Zha[8]研究探讨了设计参数和工作条件对闭式静压推力轴承运动精度的影响。赵燕[9]研究分析了抑制滚子歪斜的高速圆柱滚子轴承设计，从理论上分析了挡边负背角、挡边间隙及滚子摆角之间的关系，验证了改进措施的合理性，并且进行了实际应用。

基于以上学者的研究，本文主要针对某航空发动机主轴轴承，要求能够满足高温、高速、重载和长寿命等需求开展了正向设计研究，为了满足主机特殊工况需求，轴承设计时经多方案论证，以轴承常规仿真软件Cobra作为仿真计算平台。考虑到在计算的过程中，内、外沟曲率系数和径向游隙对轴承性能的影响较为显著，因此选取内、外沟曲率系数和径向游隙为三个因素，即自变量，以轴承寿命、内圈接触应力和外圈接触应力为三个目标，分别建立三个目标函数，采用功效系数法确定统一目标函数作为响应值，最终获得了自变量与响应值间的数学回归模型，对回归模型进行优化，得到最佳的参数优化组合，并进行了有效验证。

1 轴承建模

轴承设计时，采用通用计算公式对每一个参数进行数值给定，根据计算结果用三维建模软件UG建立三维模型，如图1所示。个别细小特征对轴承的性能影响很小，在设计建模时直接对局部特征进行处理即可，但是一些主要参数在轴承设计过程中，对轴承的性能影响很大，这时，就需要对轴承进行参数优化设计。

图1 轴承三维模型

本文以某发动机主轴轴承C276119NW1 (H)为例，外形尺寸为95 mm×145 mm×24 mm，在转速9000 r/min、轴向载荷3000 N、径向载荷1000 N时，计算轴承的寿命和内、外圈接触应力[10]。

2 优化设计

2.1 基于单因素法进行轴承性能分析

针对轴承的工况、材料、几何参数、粗糙度等几个方面因素，采用Cobra软件，以单因素方法，采用时间占比最长的工况，分别计算各个因素下的轴承寿命、接触应力和值，然后利用excel软件，绘制各个因素与轴承寿命、接触应力和值的曲线，分析径向载荷、轴向载荷、工作温度、内圈转速，内、外圈材料，内圈沟曲率系数、外圈沟曲率系数、滚动体直径、滚动体数量、径向游隙、垫片角，内圈沟道粗糙度、外圈沟道粗糙度、滚动体粗糙度等各个因素对轴承寿命、接触应力和值的影响。

根据各单因素对性能的影响，分别得出以下结论：

（1）随着径向载荷的增大，轴承寿命迅速减小后缓慢不变，轴承内、外圈应力呈现增大趋势，轴承内、外圈值变化不大；

（2）随着轴向载荷的增大，轴承寿命迅速减小后几乎不变，轴承内、外圈应力呈现增大趋势，轴承内、外圈值缓慢变小；

（3）随着工作温度的增大，轴承寿命先缓慢增大后减小，轴承内、外圈应力呈现减小趋势，轴承内圈值先不变后减小、外圈值先增大后减小；

（4）随着内圈转速的增大，轴承寿命增大，轴承内圈应力缓慢减小、外圈应力增大，轴承内、外圈值呈现增大趋势；

（5）三种材料中（8Cr4Mo4V、ZGCr15 、G13Cr4Mo4Ni4V），8Cr4Mo4V的材料对应的轴承寿命最大、应力最小，三种材料的值基本一致；

（6）随着内沟曲率系数的增大，轴承寿命先增大后减小，轴承内圈应力增大、外圈应力缓慢增大，轴承内、外圈值呈现不变趋势；

（7）随着外沟曲率系数的增大，轴承寿命逐渐减小，轴承内圈应力基本不变、外圈应力增大，轴承内、外圈值呈现不变趋势；

（8）随着滚动体直径的增大，轴承寿命逐渐增大，轴承内、外圈应力减小，轴承内、外圈值呈现缓慢增大趋势；

（9）随着滚动体个数的增大，轴承寿命逐渐增大，轴承内、外圈应力减小，轴承内、外圈值呈现缓慢不变趋势；

（10）随着径向游隙的增大，轴承寿命逐渐减小，轴承内、外圈应力增大，轴承内、外圈值呈现缓慢不变趋势；

（11）随着垫片角的增大，轴承寿命逐渐减小，轴承内、外圈应力基本不变，轴承内、外圈值呈现缓慢不变趋势；

（12）随着内圈沟道粗糙度的增大，轴承寿命逐渐减小，轴承内、外圈应力基本不变，轴承内圈值逐渐减小、外圈值呈现缓慢不变趋势；

（13）随着外圈沟道粗糙度的增大，轴承寿命逐渐减小，轴承内、外圈应力基本不变，轴承内圈值缓慢不变、外圈λ值呈现逐渐减小趋势；

（14）随着滚动体粗糙度的增大，轴承寿命逐渐减小，轴承内、外圈应力基本不变，轴承内、外圈值呈现缓慢减小趋势。

若求解的变量为内沟曲率系数f、外沟曲率系数f和径向游隙g，且三个因素为连续值，目标值为多个时，若单个目标分析时，变量无法是一个确定的值而是一个范围，故本文采用功效系数法[11]；若将所有变量全部分析时，需要列出全部设计方案，工作量的规模将很大，因此本文寻求一种可以得到最优水平组合且高效率的试验设计方法，故采用正交试验设计优化方法，正交试验设计的特点是用部分试验的结果来代替全面试验，通过对部分试验结果的分析，了解全面试验的情况[12]。

2.2 功效系数法

功效系数法是根据多目标规划的原理，把所要评价的各项指标分别对照自己的标准，并根据各项指标的权重系数，通过功效函数转化为可以度量的评价分数，再对各项指标的单项评价分数进行加和，求得综合评价分数。

功效系数法在计算时比较繁琐，但在后期处理数据时比较容易，此次优化设计有3个目标函数：寿命1、内圈应力2、外圈应力3，为了消除各个分目标函数值量级及量纲的影响，采用功效系数法对各目标函数值进行处理。

设寿命函数最大值和最小值分别为max1＝1max，min1＝1min。对于寿命是目标函数值越大越好，如图2所示，则有：

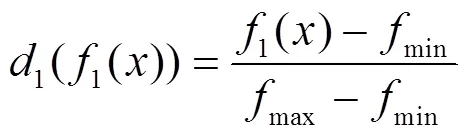
设内圈应力函数最大值和最小值分别为max2＝2max，min2＝2min。对于内圈应力是目标函数值越小越好，如图3所示，则有：

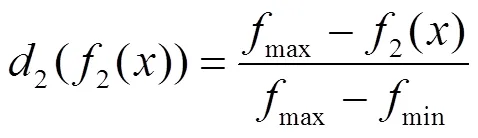
同理得到外圈应力目标函数3(3())为：

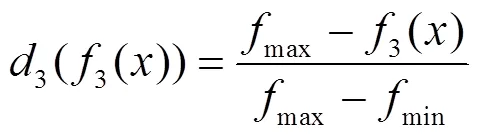
根据工况和实际生产经验选择目标函数的加权因子，根据函数的重要程度选取权数，重要性越高权数越大，整体要满足加权和为1。对于该轴承，内外圈接触应力最重要，疲劳寿命最不重要，因此寿命加权系数取1＝0.2，外圈应力加权系数2＝0.4，内圈应力加权系数3＝0.4，综合考虑的统一目标函数为：

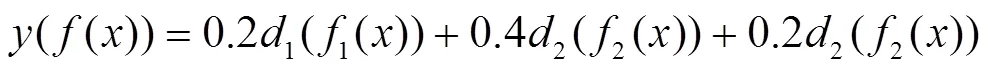
2.3 正交试验设计方案及计算结果

根据设计经验以及前期的单因素数据分析结果，最终以内沟曲率系数f、外沟曲率系数f和径向游隙g为3个因素。采用正交旋转试验方法，试验的各因素范围结果如表1所示。

表1 试验因素水平

首先确定组合设计具旋转性的星号臂为：

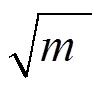
即m＝8，进而求得星号臂＝1.682。

试验总数计算如下：

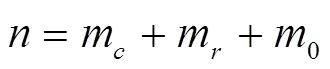
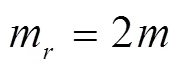
式中：m为分布星号臂球面上的试验点；0为重复试验的次数，本试验0＝9。

求得m＝23，即共进行23次试验。

则有零水平数值0j、变化区间Δ为：

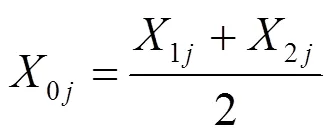
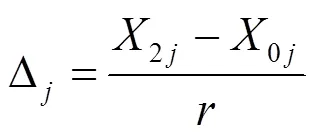
式中：2j、1j（＝1,2,……,）为第个因素的上下限。

式（8）、（9）代入1j＝0.515、2j＝0.535，求得：0j＝0.525、Δ＝0.006。

对每个因素X（＝1,2,……,）的取值做线性变换得到的因素水平编码表如表2所示。则试验方案及结果如表3所示。

2.4 回归分析

2.4.1 回归模型及其显著性分析

对表3的试验数据，采用Design-Expert软件进行二次回归分析，内沟曲率系数、外沟曲率系数、径向游隙对统一目标的回归方程为：

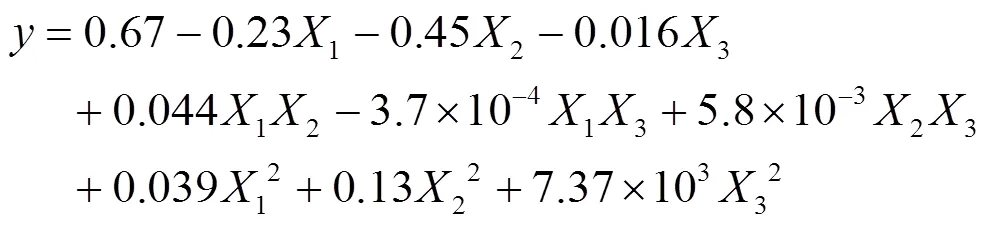
对该回归方程进行方差分析的结果如表4所示。根据方差分析的结果，对回归方程的拟合度和显著性检验。可知，在这个模型中1、2、12对模型的影响为极显著，22对模型的影响为显著。通过方差分析结果可知，模型的显著性检验＝26.32、＜0.0001，表明该模型极显著。而模型的失拟性检验＝0.89、＝0.5307＞0.05，说明失拟性检验不显著，模型在选择的参数范围内，该模型拟合的程度较好。

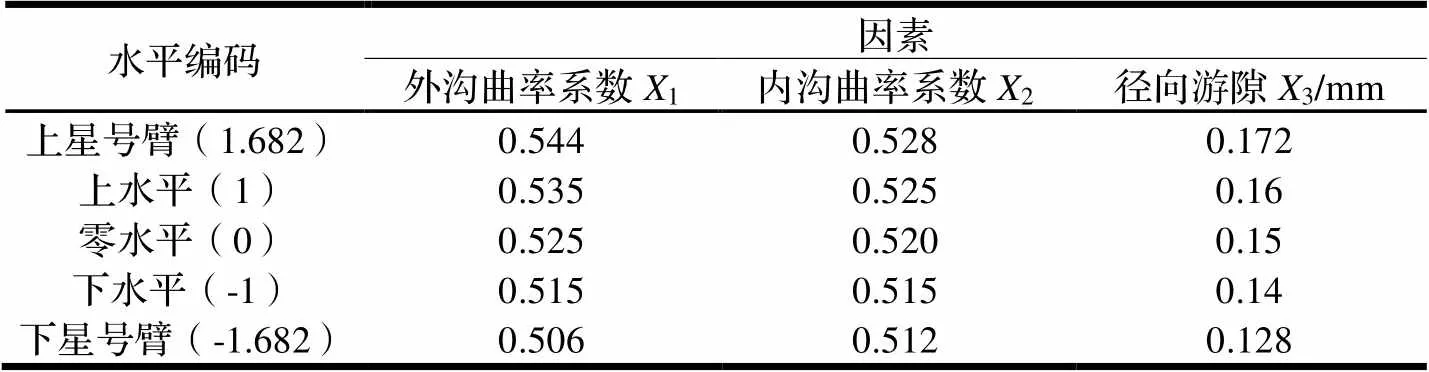
表2 试验因素水平

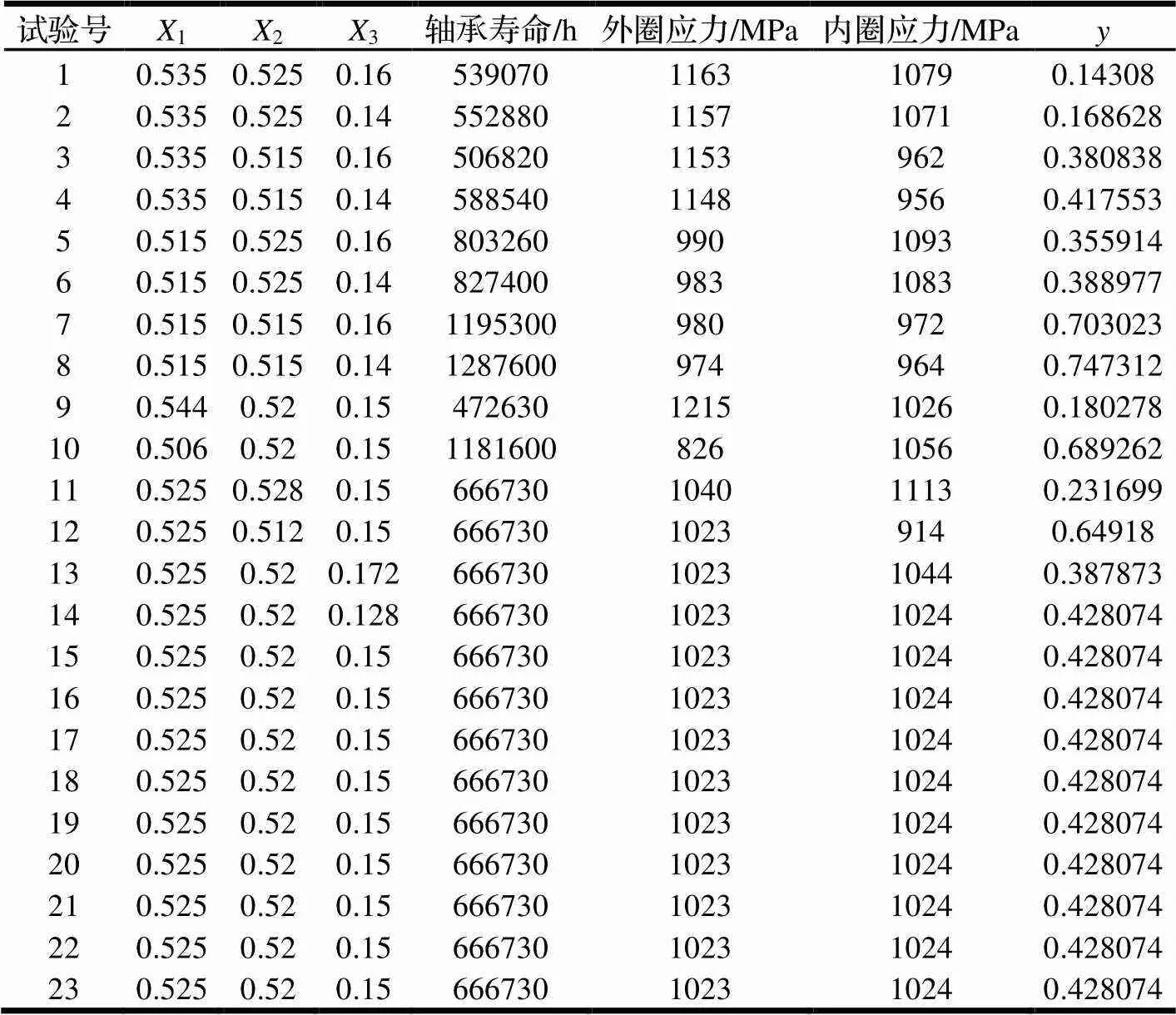
表3 试验方案及结果

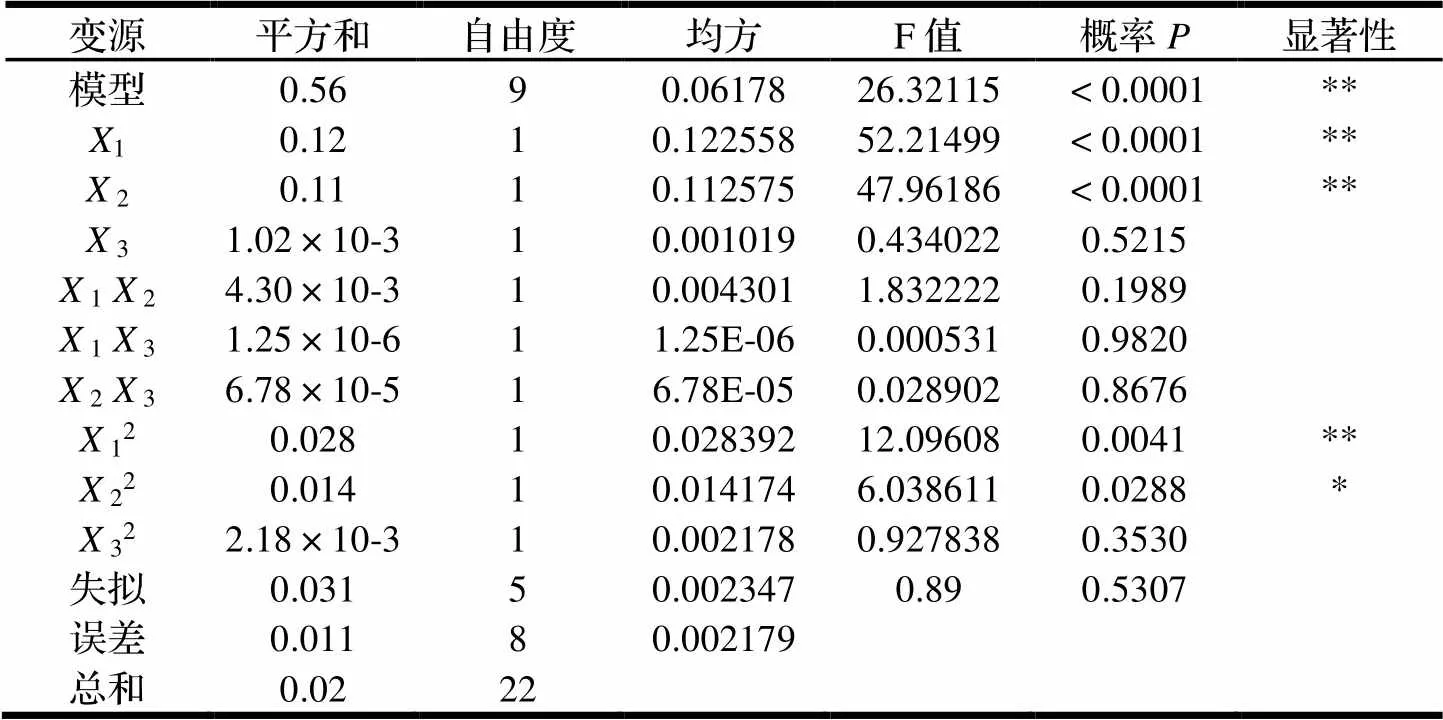
表4 方差分析

注：*表示小于0.05表明模型或考察因素显著影响；**表示小于0.01表明影响极显著。

2.4.2 回归模型的确定

对各回归系数进行检验分析，剔除模型中置信度在0.05以下的不显著系数项，获得各因素对轴承的简化回归模型，为：

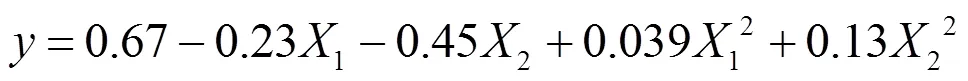
2.4.3 响应曲面分析

为了更好的解析各因素对统一目标函数的影响，针对三因素二次回归正交旋转试验，将其中一个因素固定在零水平，考察其它两个因素对统一目标的影响。但是根据该模型得到仅有外圈沟曲率系数和内圈沟曲率系数的交互项为极显著，其它交互项不显著，因此仅需要对外圈沟曲率系数和内圈沟曲率系数的交互项进行响应曲面分析。

将径向游隙固定为零水平（即0.15 mm），研究外圈沟曲率系数和内圈沟曲率系数对统一目标的影响，由图4可见，对于内沟曲率系数轴，统一目标随外沟曲率系数的增大先减小后不变；对于外沟曲率系数轴，统一目标随内沟曲率系数的增大先几乎不变之后减小。

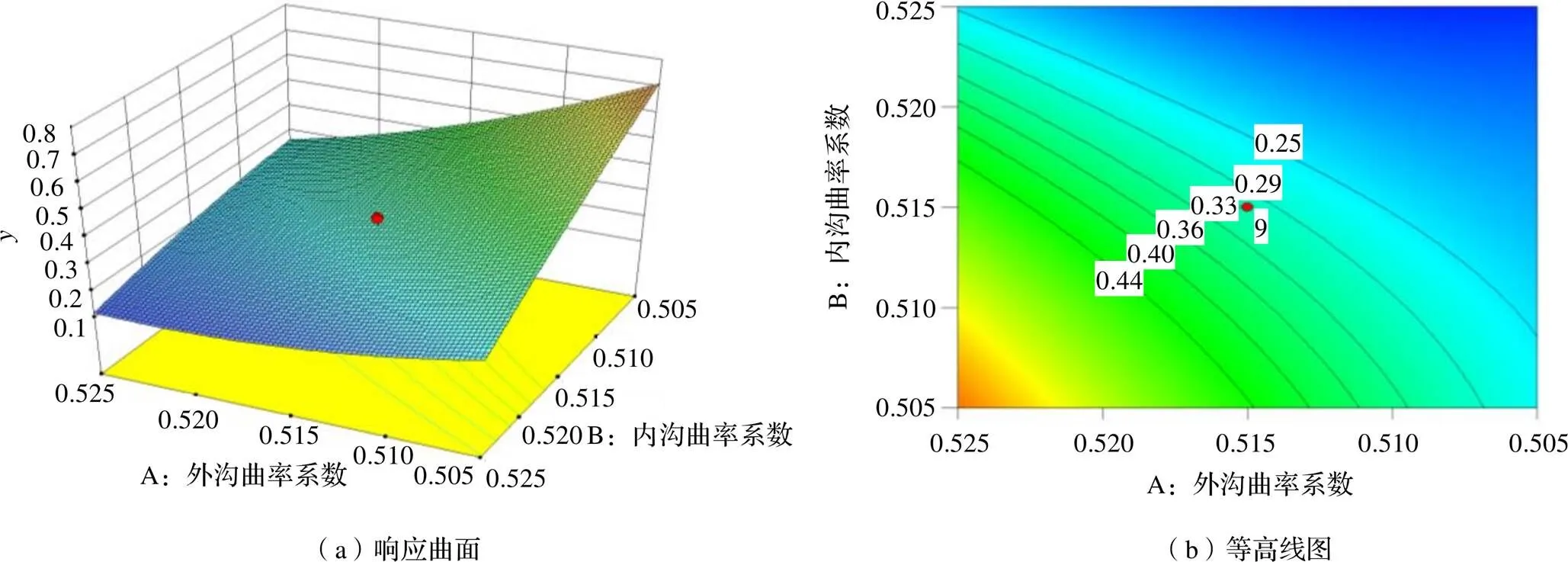
图4 外圈沟曲率系数和内圈沟曲率系数响应曲面分析（径向游隙为0.15 mm）

2.4.4 参数优化及验证

利用Design-Expert 8.0.5软件进行参数优化，优化结果为：内沟曲率系数0.515、外沟曲率系数0.515、径向游隙0.14 mm时，统一函数值为0.645，轴承寿命为1.04×106h、外圈应力为965.683 MPa、内圈应力为964.527 MPa。如图5所示。

采用Cobra软件进行仿真验证，当内沟曲率系数为0.515、外沟曲率系数为0.515、径向游隙为0.14 mm时，轴承寿命为1.3×106h、外圈应力为965 MPa、内圈应力为951 MPa。

3 结论

采用正交试验设计方法，以功效系数法确定统一函数，分析相互因素对轴承性能的影响；优化设计参数，确定最佳的参数组合为内沟曲率系数0.515、外沟曲率系数0.515、径向游隙0.14 mm；并进行仿真验证，从而完成了该轴承的设计，且优化设计的产品目前已经通过了450小时耐久性试验和50小时性能试验，为后续的轴承设计提供理论依据。

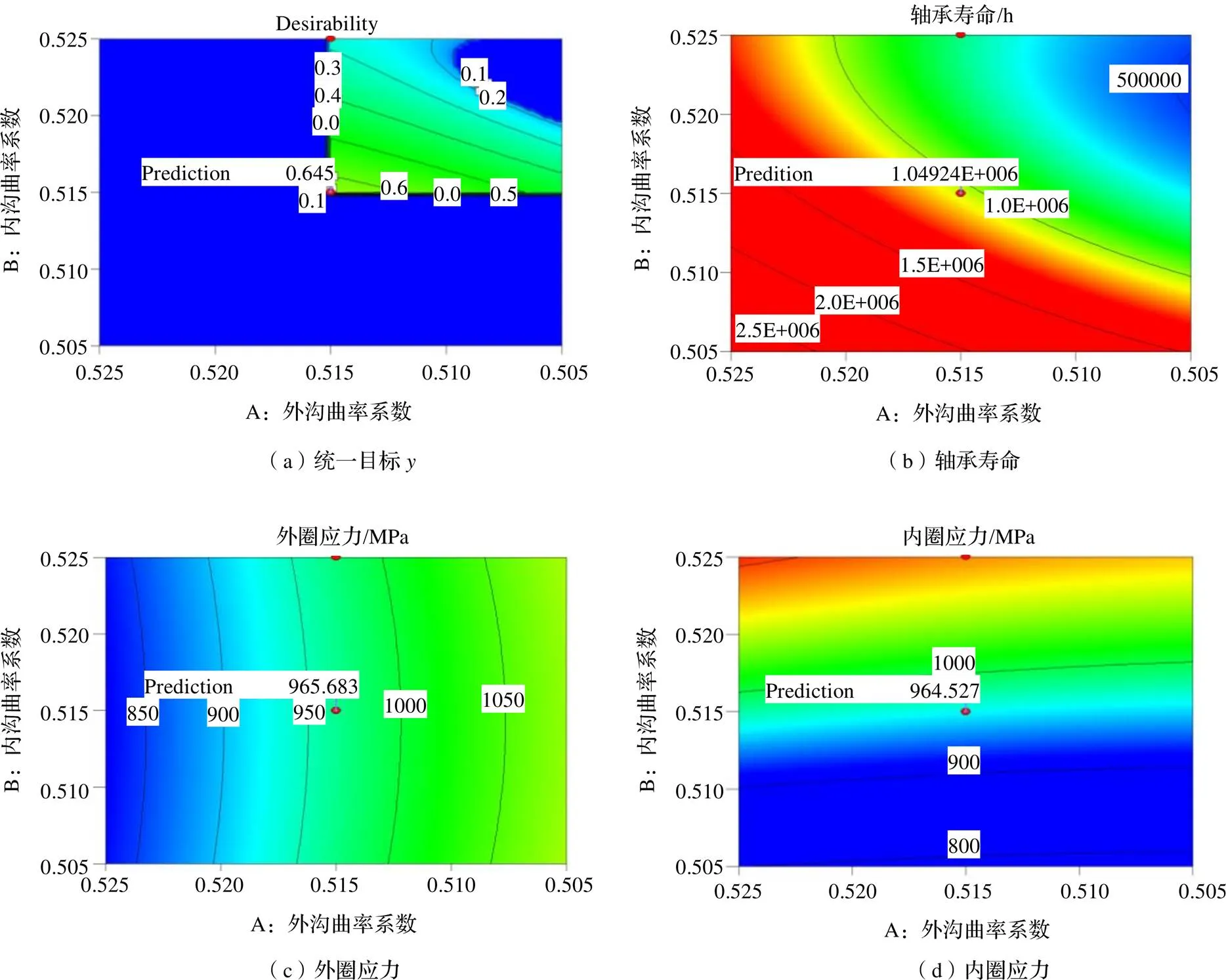
图5 参数优化结果（径向游隙为0.14 mm）

[1]欧昭，胡真清，黄日恒. 基于ANSYS的主轴箱优化设计[J]. 机械，2019，46（12）：61-66.

[2]朱亮亮，林素敏，吕秋硕，等. 滚动轴承寿命计算方法的优化[J]. 机械，2015，42（2）：20-24，40.

[3]段宏，李光俊，郭和一，等. 沉降离心机滚动轴承磨损可靠性分析及优化设计[J]. 组合机床与自动化加工技术，2020（4）：88-90，94.

[4]李昭昆，雷建中，许海峰，等. 国内外轴承钢的现状与发展趋势[J]. 钢铁研究学报，2016，28（3）：1-12.

[5]YB 4107－2000，航空发动机用高温渗碳轴承钢[S]. 2000：1-5.

[6]金燕，刘少军，张建阁. 基于遗传算法优化的人工神经网络下高速滚动轴承的疲劳可靠性[J]. 航空动力学报，2018，33（11）：2748-2755.

[7]Jun Zha，Yaolong Chen，Penghai Zhang，et al. Effect of design parameters and operational conditions on the motion accuracy of hydrostatic thrust bearing. Proceedings of the Institution of Mechanical Engineers，2020，234（8）：1481-1491.

[8]吕凤鹏，李朝阳，黄健，等. RV减速器转臂轴承的优化设计[J]. 中国机械工程，2020，31（9）：1043-1048.

[9]赵燕，毕明龙，石东丹. 基于抑制滚子歪斜的高速圆柱滚子轴承设计[J]. 轴承，2018（12）：14-16.

[10]万长森. 滚动轴承的分析方法[M]. 北京：机械工业出版社，1987.

[11]王东峰，叶军，杨伯原，等. 双列角接触球轴承的多目标优化设计[J]. 轴承，2007（8）：8-10.

[12]魏棵榕，尹自强，刘强，等. 双锥静压轴承结构设计与FLUENT仿真分析[J]. 机械，2019，46（5）：8-13，18.

Optimum Design of Spindle Bearing Parameters for an Aeroengine

FAN Hongwei1，AI Qingmu2，LI Jiaxin1，ZENG Zhaoyang1，LIU Sen3

( 1.School of Mechatronics Engineering,Harbin Institute of Technology, Harbin 150001, China; 2.School of Astronautics,Harbin Institute of Technology, Harbin 150001, China;3.AECC Harbin Bearing Co., Ltd., Harbin 150027, China)

With the development of bearing life research, it is necessary to divide the influencing factors of bearing performance to make them more specific and formulaic. In order to improve the reliability of bearings and optimize the design parameters of bearings, the influence of curvature coefficient of inner and outer groove and the radial clearance on the performance of bearings are simulated and analyzed by using the experimental design method of Box-Behnken and Cobra software. The curvature coefficient of inner and outer groove and radial clearance are selected as independent variables, and the unified function y is determined as the response value by the efficiency coefficient method. The mathematical regression model between the independent variable and the response value is obtained, which can more accurately optimize the determined value of the unified function. The results show that the inner and outer groove curvature coefficient have the most significant effect on the bearing performance, while the radial clearance has no significant effect. The optimum parameters are inner groove curvature coefficient 0.515, outer groove curvature coefficient 0.515, radial clearance 0.14mm, uniform function y value 0.696, bearing life 1.04×106h, outer ring stress 965.683 MPa and inner ring stress 964.527 MPa.

parameters optimization；groove curvature coefficient；high reliability

V233.4+5

A

10.3969/j.issn.1006-0316.2020.11.003

1006－0316 (2020) 11－0017－07

2020－06－19

范红伟（1988－），女，黑龙江哈尔滨人，硕士，工程师，主要研究方向为机械设计制造及其自动化，E-mail：fanhongwei0401@hit.edu.cn。