未熔合对厚板多层多道焊残余应力影响的数值模拟
2021-01-19纪延涛郭春荣尚文锋李长安秦国梁刘顺刚
纪延涛, 郭春荣, 尚文锋, 李长安, 秦国梁, 刘顺刚
(1.中石化胜利油建工程公司,山东 东营 257061;2.山东大学 ,济南 250061;3.中国电建集团核电工程公司,济南 250100)
0 前言
X70管线钢是控轧控冷的微合金钢,具有高强度、高冲击韧性及优良耐腐蚀性等力学性能,是目前油气输运管道的主要用材[1-2]。大直径厚壁管道环焊缝焊接时采用由内到外的焊接顺序,在背面成形不佳时往往会在打磨内壁焊缝后进行补焊,受制于管道内狭小的空间,焊接工艺不当极易在补焊时造成未熔合等缺陷[3]。未熔合缺陷容易造成应力集中,叠加厚壁管道环焊缝固有的残余应力容易对管道运行安全造成不良影响。
采用试验方法对焊接过程进行研究并改进焊接工艺往往需要高昂的成本,造成人力物力的浪费,目前数值模拟方法已成为研究多层多道焊接过程的重要手段。Deng等人[4]建立了非耦合的热力多层多道焊接有限元模型,将计算的温度场作为热边界条件进行应力计算。丁文斌等人[5]对平板对接多层多道焊的温度场分布规律进行了数值模拟研究,利用“生死单元”技术模拟焊接材料的填充过程。Xing等人[6]对60 mm特厚钢板多层多道焊过程进行了三维瞬态温度场数值模拟。胥国祥等人[7]建立了超细晶Q460高强钢厚板多层多道GMAW焊的有限元分析模型,研究了坡口形式对温度场分布及焊缝横截面形状的影响,并计算了接头的晶粒尺寸。此外,对于多层多道焊接头残余应力的研究也多有报道[8-12]。
现阶段国内外学者对厚板多层多道焊的数值模拟研究大多针对接头显微组织和工艺参数优化等,对于多层多道焊容易出现的焊接缺陷问题研究较少[13-14]。
为了研究内壁未熔合缺陷对焊后残余应力的影响以及对管道运行安全的影响,建立了X70管线钢厚板多层多道焊接有限元计算模型,在模型中预置了未熔合缺陷,数值分析焊接过程温度场、应力场和焊后残余应力,并根据管线实际运行工况等效模拟了未熔合缺陷对管道应力分布的影响。为焊接工艺设计、焊接施工方案制定、管道运行安全提供理论依据,并通过工艺试验验证了有限元数值分析结果的准确性和可靠性。
1 有限元数理建模
1.1 试验条件及模型建立
实际X70钢非等厚大直径管道环焊缝焊接,壁厚分别为17.5 mm和14.6 mm,厚壁尺寸过渡至坡口处与薄壁相等,预制V形坡口,坡口角度55°,钝边2 mm。打底焊和补焊采用焊条电弧焊,填充焊和盖面焊采用自保护药芯焊丝半自动焊,共计5层7道焊缝。各层焊接工艺参数见表1。

表1 焊接工艺参数
相关研究表明,在保证焊接达到准稳态所需焊缝长度的前提下,采用小尺寸三维平板对接焊缝模型代替全尺寸环焊缝模型可以在较少的计算成本下实现近似的模拟结果[8]。图1为几何模型及未熔合设置示意图。根据前期研究,焊缝长度达到120 mm时可以达到焊接过程准稳定状态,因此单侧试件长和宽分别为120 mm和100 mm,如图1a所示。对于未熔合等焊接缺陷的数值模拟研究十分有限[15],如何在模型中合理设置未熔合缺陷有待进一步系统研究。文中根据多层多道焊缝中实际观测到的未熔合尺寸、位置,在模型中考虑了未熔合的三维特征及其造成的材料不连续性,设定未熔合缺陷为楔形,尺寸为1 mm×1 mm,长度为25 mm,预置在焊缝长度方向中心位置补焊焊根处,如图1b所示。

图1 几何模型及未熔合设置示意图
研究的重点在于焊接应力场的分析,模拟焊丝填充过程及熔池动态行为意义不大,因此该模型中采用预置焊缝的方法,即将每道焊缝预先设置的接头内,采用生死单元技术依据焊接顺序进行逐层填充激活[16]。针对焊缝区域温度和应力的高梯度分布特点,采用非均匀网格技术对焊缝区域进行局部细化。建立的有限元模型以焊接方向为x轴、以板厚方向为y轴。板材上表面平行于xoz平面,并在o-xyz局部坐标系中定义热源中心。
1.2 热源模型建立
在多层多道焊接过程中,焊接热输入来自电弧热和过热熔滴。电弧热分布模式具有体积热源特征。熔化的焊材形成过热熔滴,在熔滴过渡过程中将一部分热量和动能带入熔池。综上考虑,该有限元模型中焊接热输入采用混合体积热源模型计算,包括半椭球体电弧热源模型和均匀柱体分布的熔滴热源模型,相对应的热流密度为:

混合体热源总能量密度为:

式中:a为半椭球体热源模型的主轴;b为半椭球体热源模型的副轴;c为半椭球体热源模型的熔深;U为电弧电压;I为焊接电流;η1为半椭球热源的热效率大小;η2为熔滴热源的热效率大小;r为熔滴热源模型的半径;h为熔滴热源模型的熔深。式中参数的取值通过前期试算确定,以模拟熔池尺寸与实际熔合线尺寸近似相等为依据。经多次模拟,最终参数取值见表2。

表2 热源参数取值
1.3 多层多道焊计算条件
为降低计算复杂程度,节省计算时间成本,在多层多道焊数值模拟时对材料做出以下假设和简化:①材料的屈服服从Von Mises屈服准则;②材料在塑性区的行为服从塑性流动准则和强化准则;③忽略材料的组织变化对材料力学性能的影响;④模型为连续介质,忽略可能发生的缺陷;⑤焊缝金属和母材具有相同的材料参数。为准确地模拟焊接过程,考虑了材料性能随温度的变化,模型中所采用的材料热物性参数如图2所示。
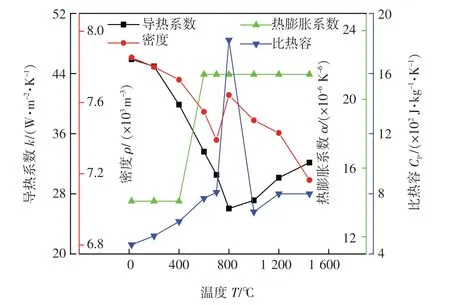
图2 X70钢热物性参数
1.4 管道受力等效处理
管道正常运行压力为8.4 MPa,对于平板对接焊缝无法在模型中直接施加内压载荷,因此有必要采用材料力学分析及数学解析计算求得内压载荷对环焊缝的影响,并等效施加到X70管线钢平板对接焊缝模型中。
对于薄壁管,其环向应力,即沿环焊缝方向应力为:

式中:P为管道内压,正常运行时为8.4 MPa;D为管道平均直径,即内外径中间值,管道实际尺寸为1 001.4mm;S为壁厚,采用薄壁侧数据,为14.6 mm。
经代入数据计算,环向应力,即环焊缝轴向拉应力约为288 MPa,如图3所示。为验证解析计算数据准确性,建立了三维薄壁管状有限元模型模拟了小段管道在8.4 MPa内载荷下的应力分布。等效应力分布显示管道整体受力较均匀,整体等效应力在283~290 MPa范围内;径向应力分布显示,受管道膨胀趋势影响,初始8.4 MPa的压力载荷得到一定的释放,管道内壁压应力约为6.2 MPa,管道外表面压应力约为2 MPa,;环向应力分布显示,管道各处环向应力分布基本均匀,约为284 MPa,仅在壁厚方向存在较小的差异,该数值与解析计算结果相近,证明了计算结果的准确性;轴向应力分布显示,管道最大仅受到数千帕的轴向应力作用,远小于其他形式应力,可忽略不计。

图3 工况下管道各向应力分布
经过解析计算与数值模拟,获得了管道的各向应力分布,对于局部环焊缝的数值模拟,确定其应受到约280 MPa左右沿焊缝方向拉应力作用,焊缝底部沿壁厚方向受到约6.2 MPa压应力作用,垂直于焊缝方向受力较小,可忽略不计。
2 温度场与应力场试验验证
2.1 温度及应力测量
为了验证所建立多层多道焊接数值模拟模型的准确性,对特征点温度和应力进行了试验采集。实际焊接中17.5 mm厚板侧厚度过渡为人工打磨减薄,存在一定不均匀性,因此在采用热电偶检测焊接过程中的热影响区温度时,测温点为14.6 mm钢板内外壁距离坡口10 mm处,避免17.5 mm板一侧可能存在的厚度过渡不均匀造成测温位置偏差。采用盲孔法测残余应力时,因盲孔法测表面应力的特点,为减小薄壁对测量准确性的影响,测取了17.5 mm厚板外壁距焊趾15 mm处特征点的残余应力值。
2.2 数值计算结果的试验验证
通过试验测试获得了不同道次特征点的热循环曲线,如图4所示。对比模拟值和实测值发现热循环曲线演变趋势近似吻合,A,B两个特征点在不同道次的峰值温度、升温速率的模拟值和测量值的误差百分比均在15%以内,因此所建立的有限元模型能较准确地描述X70管线钢的焊接热过程。图5为数值模拟的接头残余应力分布结果与焊后试验测量结果的对比,可以看出,沿焊缝方向分布的残余应力趋势基本吻合;计算发现测量位置上的残余应力模拟值与实测值误差最大不超过18%,焊缝中段的模拟值与测量值十分接近,均在180 MPa左右。综合上述结果可以说明,建立的X70管线钢多层多道焊接残余应力计算模型具有较可靠的准确性,能够进一步为未熔合缺陷对应力分布和管道安全影响的计算提供理论依据。
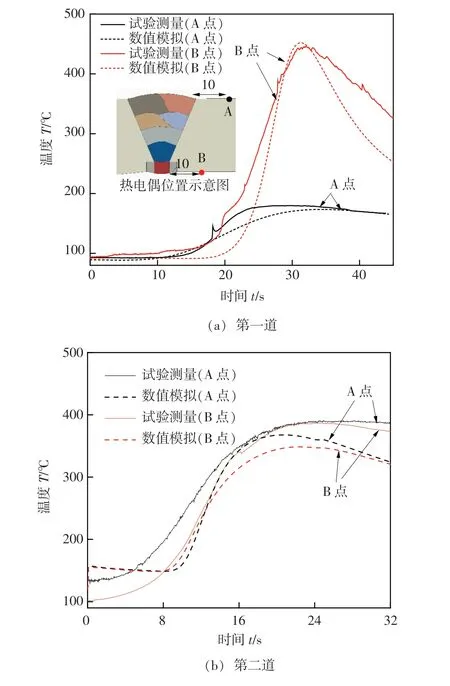
图4 不同道次特征点热循环曲线对比

图5 残余应力模拟与测量结果对比
3 模拟结果与分析
3.1 温度场演变
图6为第1层打底焊的温度场云图演变过程。图中超过1 445 ℃的区域即为焊接熔池范围,可以看出焊接开始后熔池很快进入准稳定状态,即峰值温度和熔池尺寸基本保持不变。在热源中心经过后,焊缝区域温度迅速下降,第1层焊接完成20 s后,焊道最高温度由超过1 445 ℃下降到240 ℃。
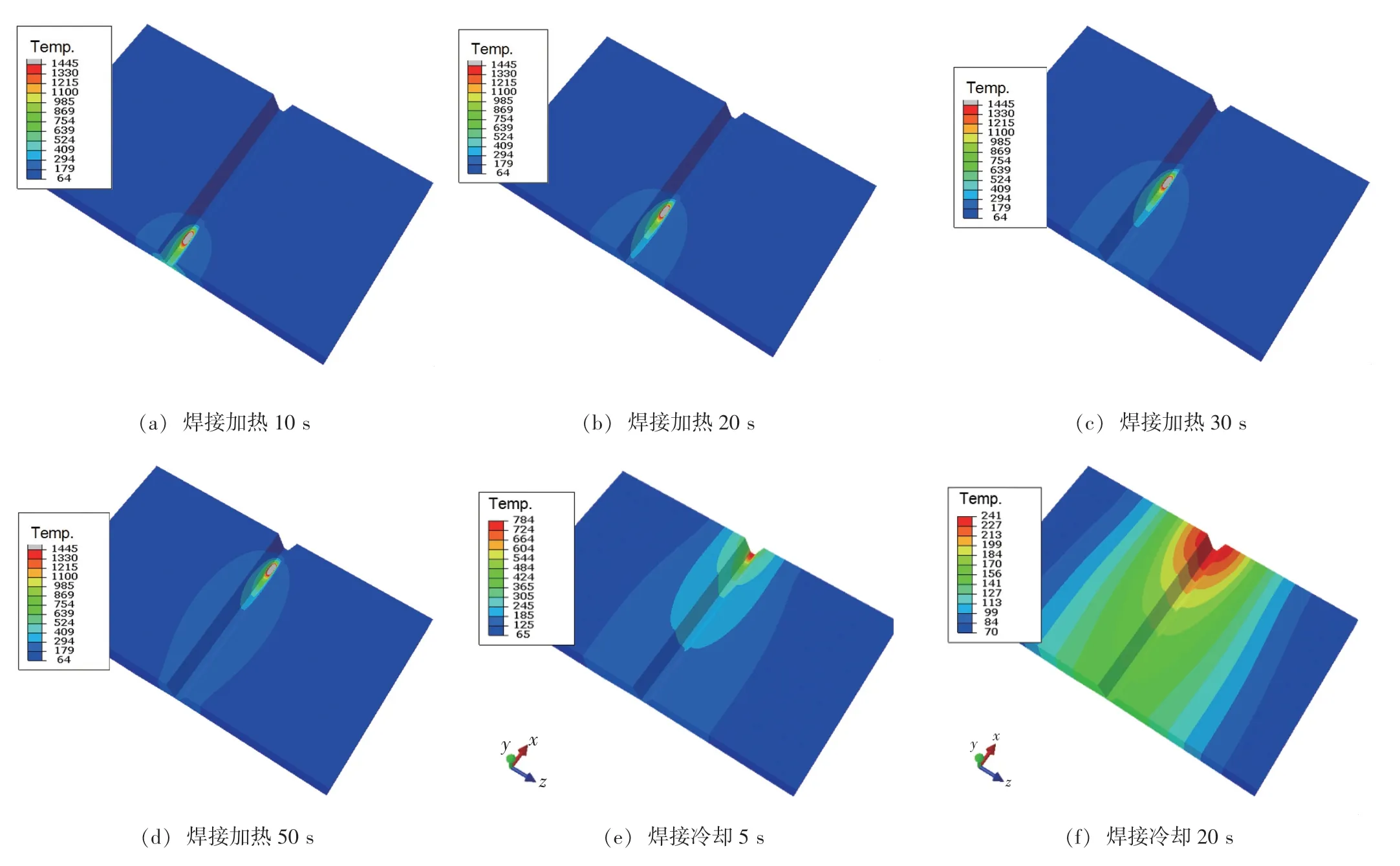
图6 典型焊接过程温度场演变
图7为第1层打底焊在不包括补焊的多层多道焊过程中的焊接热循环曲线。热循环曲线显示第1层焊缝中心和热影响区均经历了7次升温降温过程,且焊接过程升温和冷却都十分剧烈。后续焊道的加热对前道焊缝类似于一种回火作用,随后焊道的焊接加热对先前焊道的再次加热作用势必改变整体的应力状态分布。前一道焊缝形成以后,转为紧邻的下一道焊缝的热影响区,其峰值温度与母材中的焊接热影响区接近,这也说明经过多次焊接热循环后先形成的焊缝的应力状态可能与母材中焊接热影响区的应力状态接近,这也是多层多道焊的典型特征。

图7 多层多道焊过程中打底层焊接热循环曲线
图8为第7道盖面焊和第8道补焊过程准稳态下热源中心横截面温度分布云图。从图中可以看出,焊缝两侧板厚虽然有一定差异,但对横截面的温度分布几乎没有影响。由于根据实际情况在补焊前设置了较长的冷却时间,母材已冷却至室温,补焊时焊缝附近区域的温度梯度更大,剧烈的升温降温过程可能会对补焊层的应力分布造成显著影响。

图8 焊接准稳态阶段横截面温度场云图
3.2 应力场演变
图9~图11为焊接过程中不同时刻的应力分布状态。每道焊缝焊接过程中,热源下方的熔池区域内材料属于无应力的液态。此外,由于熔池前方前道焊缝的约束作用,熔池前侧区域往往具有很高的应力,当焊接加热临近结束时刻,由于焊缝后方区域早已凝固并与熔池之间存在较大温度梯度,后部应力值逐渐增大。

图9 第2道中不同时刻的应力分布状态

图11 第6道中不同时刻的应力分布状态
在每道焊缝焊接完成后需控制层间温度,而在此冷却过程中,试样不同位置体现出不同的应力演变状上升,而远离焊缝的部分应力逐渐释放到较低水平,这是因为焊缝区域材料在焊接过程中经历了膨胀、熔化、凝固和收缩的变形阶段,材料的强度在高温阶段处于较低水平,而远离焊缝区域材料始终处于高强度的刚性状态,焊接时积累的内应力在冷却阶段温度均匀化过程中转移到了焊缝区域。对于两端无约束的平板对接焊而言,由于两端收缩变形过程中受到的约束较焊缝中部少,可以相对自由地发生变形,使得焊缝中间段的应力值明显高于端部。此外,焊缝两侧应力基本保持对称分布,说明两侧厚度差异未对冷却阶段应力分布造成显著影响。
3.3 未熔合对残余应力的影响
根据第四强度理论,以Mises等效应力为判断准则,当等效应力超过材料屈服强度时,表明该处发生塑性变形,而当等效应力超过材料抗拉强度时,表明该处发生断裂失效。
根据前期研究,未进行补焊的对焊试件最高应力位于打底层两侧焊趾处,两侧应力均达到468 MPa,板厚差异对应力大小影响有限。盖面层两侧焊趾也具有较高的残余应力,受焊接顺序影响,14.6 mm板厚侧焊趾处的残余应力达到430 MPa。而母材室温屈服强度约为530 MPa,抗拉强度约为622 MPa,打底与盖面焊缝焊趾处残余应力均低于母材屈服强度。
如图12所示,分别定义楔形未熔合缺陷的三条边。沿三条边提取残余应力值的结果如图13所示。沿着焊接方向,未熔合尖角边上的残余应力有增加的趋势。三个尖角边中,靠近补焊焊趾处的尖角外边残余应力最高,未熔合尖角内边的残余应力次之,远离焊趾处的尖角外边残余应力最低。未熔合处的残余应力大小介于453 ~ 470 MPa之间,最大值为470 MPa。未熔合的存在,并未使得补焊后的残余应力明显增加,且残余应力水平低于X70板材屈服强度不会导致焊缝开裂。

图12 补焊未熔合焊缝
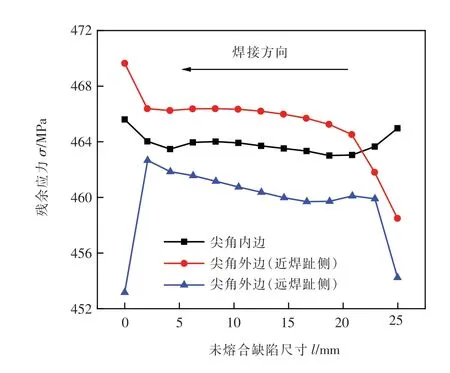
图13 未熔合各边应力分布
图14为补焊未熔合焊缝在等效工况下的应力分布情况,在内壁补焊焊缝的两侧焊趾处存在两处条状高应力区域,等效应力超过550 MPa,大于焊缝金属的屈服强度,其中未熔合一侧相对较高,未熔合两端最高等效应力可达到592 MPa,超过材料的屈服强度,这表示此处金属可能存在小范围的塑性变形,一定程度的塑性变形会使金属材料强度提高并使应力得到一定释放,但最大应力与抗拉强度仍差距较大,并不会导致焊缝的开裂。等效工况下未熔合三条特征边的应力曲线如图15所示。曲线显示,未熔合尖角内边应力在550 ~560 MPa范围内,两外边的应力得到一定释放,未超过材料屈服强度。

图14 等效工况下未熔合处应力分布(Pa)

图15 等效工况下未熔合各边应力分布
等效工况下应力分布情况说明未熔合处存在应力集中并成为焊缝薄弱处,未熔合虽然不会导致焊缝的直接失效,但降低了焊缝的冗余性能,对管道的正常运行造成不良影响。因此在后续焊接工艺制定时应尽量实现良好的一次背面成形,避免补焊引入未熔合等缺陷。
4 结论
(1)基于预置焊缝和逐层填充的建模方法,建立了X70管线钢多层多道焊接有限元计算模型,将环焊缝工况受力状态等效处理后与未熔合缺陷一起引入模型,通过温度和残余应力测试验证了模型的准确性。
(2)补焊焊缝未熔合缺陷未导致焊后残余应力的明显增加,未熔合处残余应力大小介于453 ~ 470 MPa之间,最大等效应力470 MPa,未超过X70管线钢母材屈服强度。
(3)等效工况下未熔合处最高等效应力达到592 MPa,补焊焊缝的两侧焊趾处存在两处条状高应力区域,等效应力超过550 MPa,均超过母材屈服强度,但未达到抗拉强度。
