基于K-距离拓扑的分布式数据存储方法*

郎登何

(1. 重庆大学 大数据与软件学院，重庆 401331；2. 重庆电子工程职业学院 人工智能与大数据学院，重庆 401331)

随着移动互联网技术和信息技术的快速发展，越来越多的终端设备和传感器被接入互联网，产生了海量数据，令传统的数据存储方式逐渐被云存储和分布式存储所取代[1-2].

分布式数据存储采用广泛分布在不同地理区域并相互连接的成本低廉、数量众多的PC服务器来存储海量数据[3]，这种存储方式能大幅节省存储成本，但节点的可用性较低.同时，数据存储规模的不断扩大也大幅增加了系统发生故障的概率.而云存储技术可在云计算的基础上，通过应用软件和分布式文件系统、集群技术和网络技术，将不同设备和不同类型的数据相结合协同工作[4-5]，但不同位置的存储节点有着不同的存储能力和链路带宽，使得难以提高数据存取速度[6-8].

云存储概念提出的同时，云计算的安全性也受到广泛关注[9].如Google Cloud Platform和Amazon S3为用户提供了不同安全等级的加密服务，然而云存储通常需要加密庞大的数据，这将消耗大量的计算资源，且这种数据加密方式需要用户自己保管秘钥，也会导致服务质量的降低和存取时间的增加.

目前，国内外学者和专家提出了诸多方法来解决这些问题，如采用图分割的方式从数学理论的角度考虑分布式数据存储的拓扑结构，但该种方法并未综合考虑链路和节点的性能[10]；也有文献提出使用智能优化算法来选择存储节点，以降低带宽消耗并节省数据存取时间，但这种方法存在局部最优的问题且具有较高的复杂度，不适合作为数据放置策略[11].

本文综合考虑分布式数据存储的安全性和高效性，提出了一种基于K-距离拓扑的低复杂度数据放置算法.该算法通过寻找K-距离拓扑子图来实现数据的安全放置，在此基础上，采用最小化存取时间的方式合理地放置数据.

1 系统模型

本文使用网络拓扑图模型G(V，E)来表示分布式存储系统，其中，V和E分别为存储节点集合和链路集合.第i个节点的存储能力由SCi表示，链路的带宽矩阵由B表示，且对于任意的bij∈B，则有

(1)

模型中用户可以任意选择数据存储的节点来提交数据.本文将存储数据D进行分块，并用SDi表示节点i处存储的数据块，则有

(2)

本文从以下两方面保证数据的安全性：

1) 根据数据存放的距离来表示数据安全级别的高低，距离更大的数据块间具有更高的安全性；

2) 不同领域的数据具有不同的安全性.

为了实现上述安全性要求，本文提出了一种安全距离的定义：使用K表示安全距离，K=0表示数据没有安全性需求；K=1表示任意两个数据块间的距离必须大于1；K=2表示任意两个数据块间的距离必须大于2.定义fs表示计算数据间的安全距离，即

fs=minfk(SDi，SDj) (i≠j，i，j=1，2，…，V)

(3)

(4)

式中，dis(i，j)为两点之间欧式距离.

在确定数据存取的安全性条件后，对数据存取的时间进行建模，假设当前数据存储策略SD的安全距离为K，数据从节点A接入，则对任意存储节点SDi≠0，i=1，2，…，V，各节点的数据存取时间为

(5)

式中：Pi，A为节点i和节点A间的最短路径；tls，ld为链路l数据存取时间；ls，ld为两链路的起点和终点.存取所有数据块D所需的时间为

(6)

基于上述对数据安全和数据存取速率的分析，本文将分布式数据存取问题表示为：在接入点A处将给定大小的数据D进行合理分配，则在满足距离大于K且所需存取时间最小条件时，可将该问题表示为

(7)

2 数据存储算法

2.1 数据存取模型定义

本文使用K-距离拓扑子图来表示数据存储节点，以保证数据块的放置能满足安全距离的要求.

K-距离拓扑子图的定义为：假设G(V，E)为无向连通图，如果其节点集合V′⊆V满足

dis(v1，v2)≥K(∀v1，v2∈V′，v1≠v2)

(8)

则称该子图为K-距离拓扑子图.

基于上述定义可以得到K-距离拓扑子图的生成算法如下：

1) 假设需要得到的图模型为G(V，E)，安全距离为K；

2) 随机选择一个节点v；

3) 将节点v与所有到节点v的距离小于K的节点相连；

4) 执行循环比较，循环停止后得到的结果即为生成的K-距离拓扑子图.

根据该算法描述可知，对于给定的图模型G(V，E)，存在多个K-距离拓扑子图.图1为一个包含10个顶点的拓扑图，图2、3为选择不同的初始和中间节点得到的两种不同拓扑子图.其中，图2为包含节点2，4，7，9的2-距离拓扑子图，即K=2；图3为包含节点1，3，5，6，8，10的2-距离拓扑子图.从图2和图3可以看出初始节点和中间节点的选择对于构造拓扑子图异常重要.

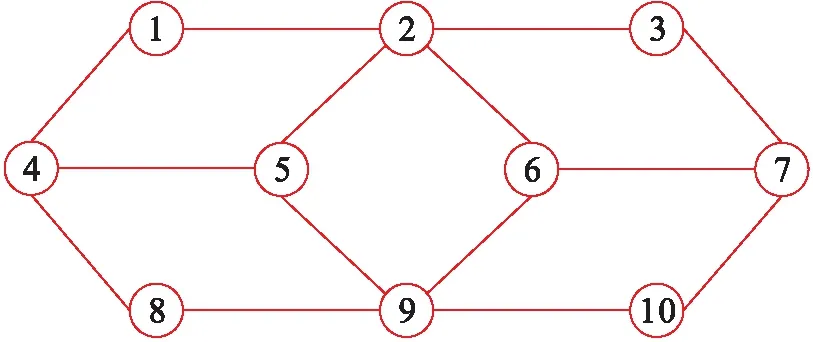
图1 10顶点网络拓扑图Fig.1 Network topology with 10 vertexes

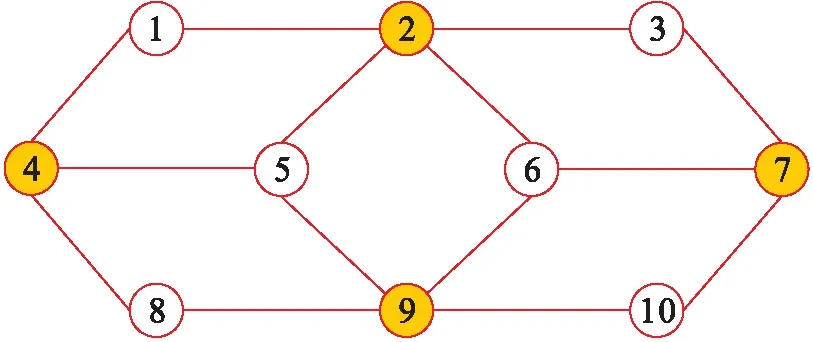
图2 2-距离拓扑子图1Fig.2 Sub-graph 1 of 2-distance topology

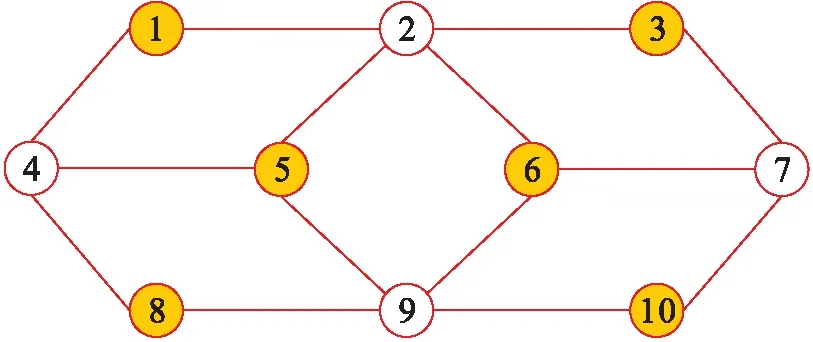
图3 2-距离拓扑子图2Fig.3 Sub-graph 2 of 2-distance topology

2.2 节点选择算法

基于上文定义的K-距离拓扑子图，本文将存储节点选择过程转化为在给定安全距离K的条件下，寻找使数据存取时间最小的K-距离拓扑子集问题.本文提出一种基于节点优先级选择的算法来求解该问题，即根据各节点的数据存取速度优先选择存取速度更快的节点和自身保护能力强的节点.

单位数据存取速度定义为

(9)

式中：Pv，A为节点v和A间的最短距离；D为数据总量.

数据存储节点选择算法具体流程如下：

1) 对每一个节点，根据式(9)计算Uv.

2) 对所有Uv按照从大到小的顺序排序，得到排序后的集合PV.

3) 计算节点A与集合PV中每一个节点间的最短距离d.

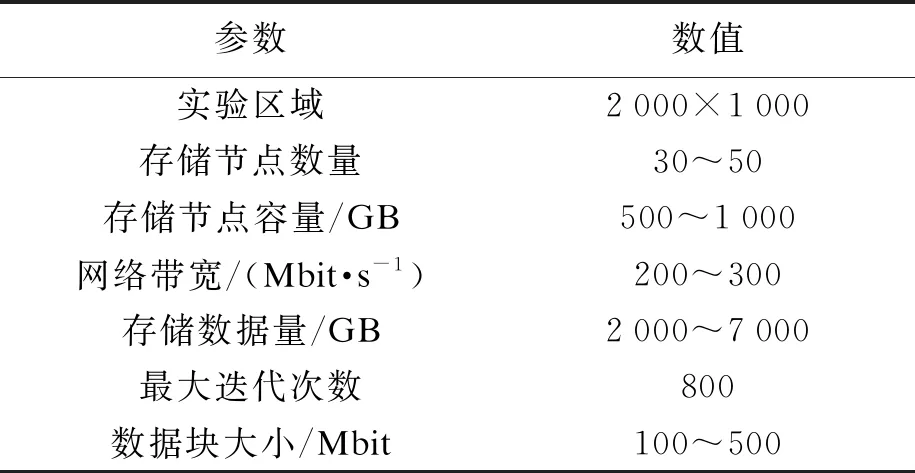
4) 当d≥K时，将该点放入最优数据存储集合；当d

本文存储节点选择算法主要分为两部分：1)按照单位存取时间排列数据存储节点；2)使用最短距离算法选择最优的数据存储序列.其中，第1部分的时间复杂度为O(V)；第2部分的时间复杂度为O(VO(E+VlgV))或O(VO(kE))，其中，E为图G的边数量，k为SPFA算法中节点进入Queue的次数.因此，本文存储节点选择算法的时间复杂度包括两种情况：最优情况下为O(kVE)，最坏情况下为O(VE+V2lgV).

3 仿真分析

本文使用Matlab和Omnet++仿真平台验证所提出的基于K-距离拓扑的高效、安全的分布式数据存储算法的有效性，并使用Internet 2拓扑图与随机拓扑图衡量该算法在不同应用场景下的性能.两种网络的具体仿真环境参数如表1所示.

表1 仿真参数设置Tab.1 Settings of simulation parameters

图4为本文使用的Internet 2拓扑图.该拓扑图由带宽为1 Gbit·s-1的节点组成，每个节点表示一个美国的城市.

本文通过与FNF算法、GA算法和kDDS算法进行比较来验证所提出算法的有效性.其中，FNF算法直接根据节点间的距离来选择存储节点以提高数据的安全性；GA算法则使用遗传算法来选择最优的存储节点来减少数据的存取时间，这种方法计算量较大；kDDS算法采用图分割理论来减少带宽和数据存取时延.

图4 Internet 2拓扑图Fig.4 Internet 2 topology graph

本文首先比较了不同数据量和网络节点情况下，各种算法在随机拓扑网络中的数据存取时间结果如图5、6所示.从图5中可以看出，相比于其他算法，本文算法所需的数据存取时间最小，且随着数据的增加，本文算法所需的存取时间增加量最小、最缓慢.这是因为所提出的算法能通过选择链路状况最优的节点来减小数据的存取时间.从图6可以看出，即使网络节点数量不断提高，所提出算法的数据存取时间仍稳定且较小.相对于其他算法，本文算法能减少60%～70%的存取时间.在随机拓扑网络中的测试结果表明，所提出的算法在满足安全距离的情况下，能通过选择性能最优的节点来存储数据，以减小数据的存取时间.

图5 随机拓扑下不同数据量的数据存取时间Fig.5 Data access time of different data volumes under random topology

图6 随机拓扑下不同网络规模的数据存取时间Fig.6 Data access time of different network sizes under random topology

图7、8为在不同数据量与网络节点情况下，各种算法在Internet 2拓扑图中的数据存取时间.

图7 Internet 2拓扑图下不同数据量的数据存取时间Fig.7 Data access time of different data volumes under Internet 2 topology

图8 Internet 2拓扑图下不同网络规模的数据存取时间Fig.8 Data access time of different network sizes under Internet 2 topology

从图7、8中可以看出，随着Internet 2拓扑图中数据量的不断增加，所有算法的数据存取时间均在增长.而本文算法的增长速度最慢，且相较于其他算法需要更少的存取时间，且随着Internet 2拓扑图数据规模的不断增加，本文算法所需的数据存取时间也是最低的.

从仿真结果可以看出，在Internet 2拓扑图和随机拓扑图情况下，本文算法均具有最低的数据存取时间.这是因为相较于其他算法，本文算法能在满足安全距离约束的条件下选择到最优的数据存储节点并使用最少的数据存取时间.

4 结 论

本文提出了一种基于K-距离拓扑的分布式数据存储方法.该算法使用K-距离拓扑子图来表示数据存储节点，来保证数据块的放置能满足安全距离的要求.同时提出了一种基于节点优先级选择的算法，将存储节点选择过程转化为在给定安全距离K条件下的拓扑选择过程.使用Matlab和Omnet++仿真平台在Internet 2拓扑图与随机拓扑图下的仿真测试结果表明，所提出的算法能在满足安全距离约束的条件下选择到最优的数据存储节点，从而减小数据存取时间.