L2 正则化粒子滤波在水下无人平台纯方位角跟踪的应用

田德艳，张小川,2，邹司宸，马士全，吕勇

(1. 青岛海洋科学与技术试点国家实验室，山东 青岛 266237；2. 海军潜艇学院，山东 青岛 266199)

0 引 言

水下无人移动平台搭载传感器进行目标探测与跟踪是当前的研究热点与难点。水下滑翔机因其低功耗、长航时、低噪声、强隐蔽性在海洋目标监测、探测方面应用广泛。将水下声学滑翔机作为移动观测站可进行目标的探测与跟踪，笪良龙教授团队[1-4]在这方面已经取得了一定的成果。但仅依赖测量数据存在弊端，当测量数据异常突变、测量丢失以及故意干扰等情况下都会影响跟踪效果，甚至导致跟踪失败。

卡尔曼滤波器作为传统最优线性递归方法，综合考虑测量值和估计值，在水下目标跟踪中得到广泛应用。但由于其基于参数的高斯滤波特性，不适合用于水下运动目标的非线性问题。对于非线性的水下目标跟踪问题，粒子滤波以其序惯蒙特卡罗的思想，趋近于最优估计，取得了一定的研究成果。李天成等[5]对粒子滤波理论、发展脉络以及研究进展做了很详细的总结分析。宋绪栋等[6]研究了几种适用于单、双观测站的水下目标纯方位角跟踪算法，并进行详细的仿真分析，结果表明非静止单观测站虽不能获得完全观测，但在一定先验信息条件下，可实现目标轨迹估计。张林琳等[7]结合水下目标的被动跟踪应用背景，比较了扩展卡尔曼滤波、不敏卡尔曼滤波以及粒子滤波在水下目标跟踪中的性能差异，表明粒子滤波能较好的用于非线性、非高斯条件下的水下目标跟踪，但是粒子滤波随着时间推移也存在粒子贫化问题导致目标跟踪变差。针对粒子滤波贫化的问题，各种重采样改进算法[8-19]相继提出，金盛龙等[20]提出一种粒子滤波的联合检测与跟踪方法，在状态滤波过程中不需要方位观测值的输入，直接根据波束能量评估粒子的似然函数，结合交叉变异算子提高粒子多样性，改善粒子贫化。此外，为了解决粒子滤波重采样引入的采样枯竭问题，正则化粒子滤波[21-23]（RPF）也被提取出来，RPF 利用概率密度原理，通过对每个粒子的核密度采样来实现对整个连续近似分布的采样，从而生成具有不同粒子位置的新粒子系统。

以上算法的改进确实在一定程度上改善了粒子贫化，减缓了粒子的发散，但是以上算法大都是基于一定的先验知识。由于水下无人平台在实际工作中，不知道自己的位置，更不知道目标初始位置的以及运动状态信息的，故以上改进方法对实际应用带来了一些限制条件。

为了解决以上存在问题，针对水下声学滑翔机探测跟踪系统，本文提出适用于该单站纯方位角跟踪测量系统的滤波方法。首先结合最小二乘拟合方法，由矢量水听器前几个周期接收数据经过复声强器后，得到的目标方位信息，作为该系统的初始状态，然后经过基于L2-RPF 算法，输出该系统对水下目标跟踪的结果。本文给出基于L2-RPF 的理论推导过程以及简化形式，仿真和试验结果表明，该方法相较于其他粒子滤波方法，能够提高目标跟踪精度，方位估计结果更接近真实值，对于真实环境具有较好的应用。

1 水下无人平台跟踪系统建模

1.1 常规单站单目标跟踪系统建模

目标跟踪方法都是基于模型的，以单个观测站单个目标为例，在水下运动目标初始状态信息以及观测站初始状态信息已知的前提条件下，可对该系统进行数学建模。

在笛卡尔坐标系下，目标的状态转移方程为：

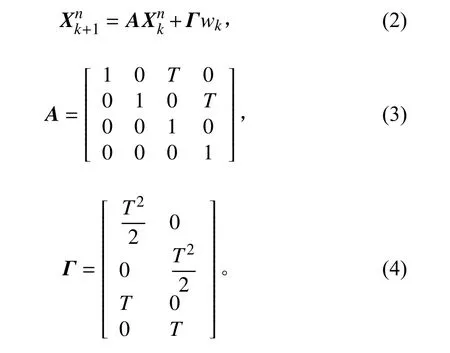
其中：T 为采样数据间隔， wk表示系统过程噪声。

若目标作匀加速运动，则目标状态量表示为：

在纯方位角跟踪系统中，测量量为Zk=[θk]， θk表示方位角，系统测量方程为：vk

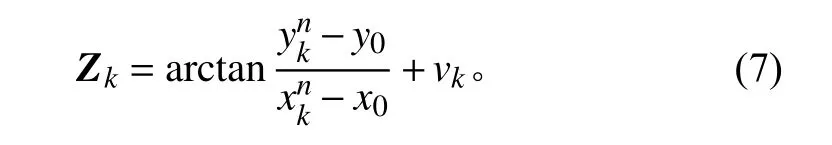
其中：为观测站的坐标， 为系统测量噪声。

1.2 实际应用环境系统建模

上述单观测站单目标探测系统基于一定的先验知识，要预先知道观测站与水下目标的初始状态信息。但实际应用时，水下目标的初始位置及运动状态都是未知的，因此，需要建立实际环境下的系统模型。结合实际项目需求，由水下声学滑翔机作为观测站，在水下作剖面滑翔进行探测跟踪。在先验知识缺失的条件下，矢量水听器被动接收信号，转换到频率域，经过复声强器后，输出由测量值得到的探测方位角。

由初始一段时间测量值经过复声强器得到的探测方位[角来拟合出]状态方程，单矢量水听器的输出量表示为P,Vx,Vy,Vz，根据复声强器法：

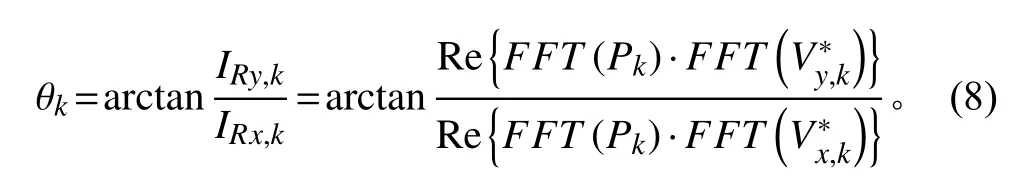
其中： θk表示k 时刻目标相对于平台的方位角度；IRy,k表示k 时刻声压与振速y 通道的互谱；IRx,k表示k 时刻声压与振速x 通道的互谱；

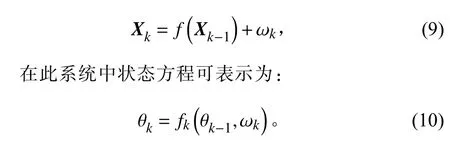
考虑到正切函数在90°和270°趋于无穷大的情况，将系统的测量方程表示为正切函数和余弦函数的分段组合，具体为：

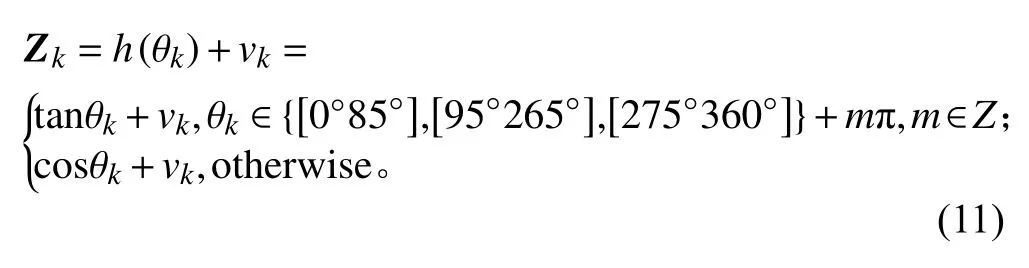
2 粒子滤波原理

粒子滤波（PF）是一种基于序惯重要性采样（SIS）的序惯蒙特卡罗方法，其不受系统线性化误差和高斯假设的限制，但存在计算量大、粒子退化问题（采样粒子枯竭）严重。为解决粒子贫化，1993 年Gordon 等提出重采样算法，重新分配所有粒子权值，但由于重采样算法是基于大权值粒子的复制保留，这样降低粒子多样性。基于此，Gordon 提出基于贝叶斯采样估计的重要性重采样滤波算法（SIR），选择最优的重要性密度函数改善粒子贫化和退化的问题。

根据上述系统模型，得到系统的状态方程和测量方程，进而可得状态转移概率密度p(xk|xk-1)和似然概率密度p(zk|xk)。粒子滤波算法通过一个重要概率密度函数来近似估计未知状态的后验概率分布p(xk|zk)，从而估计该时刻的状态变量。

该过程主要分为预测和更新两阶段。

预测：

PF 算法具体描述如下：

步骤1初始采样。从初始先验分布p(x0)中采样得到样本粒子集合

步骤2重要性采样。从重要性概率密度函数q(xk|xk-1,zk)中采样得到k 时刻粒子集 {，其中，表示k 时刻第i 个粒子的状态值，表示k 时刻第i 个粒子的权值，重要性概率密度函数一般选取为状态转移概率密度函数p(xk|xk-1)。

步骤3更新权值。根据当前测量值 zk，可计算对应粒子集 {。

其中，p(zk|xk)为似然函数，根据测量值与先验估计测量值以及测量过程噪声方差重建高斯分布，作为似然函数，更新权值：

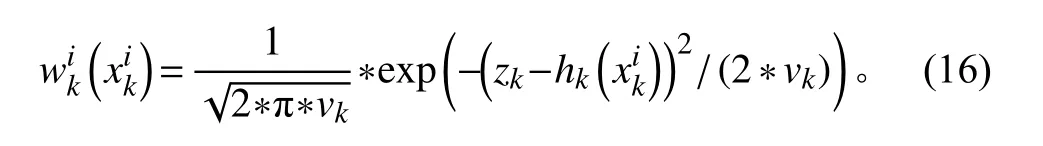
似然函数反映的是滤波器先验预测的值与传感器测量值的接近程度，两值越接近，其权值越大；反之，权值越小。

归一化权值：

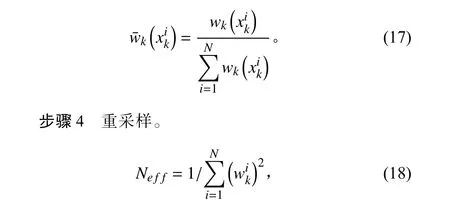
假设，Nef f＜Nth重采样得新粒子集。

步骤5状态估计。

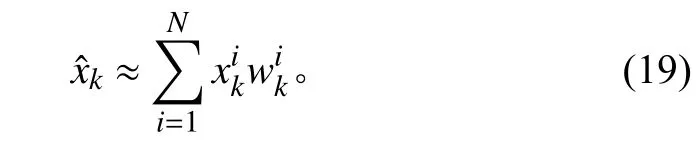
3 L2 正则化粒子滤波原理

RF 采用重要性重采样算法来改善粒子的退化问题，但随时间推移，大权重粒子被保留，小权重粒子被舍弃，导致粒子多样性减少，估计精度下降。正则化粒子（RPF）滤波结合核函数理论，将离散分布问题转化为连续分布问题，即根据密度估计理论计算出后验连续概率密度分布，从中采样得到粒子集，改善粒子退化。

RPF 是对后验概率密度函数 的连续近似分布进行重采样，从而得到粒子集：

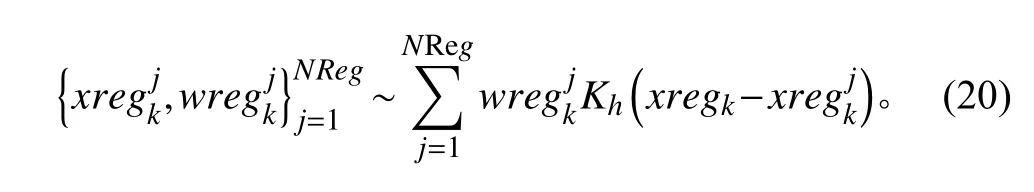
基于正则化近似连续概率密度分布函数计算得到采样正则化粒子和权值，具体描述如下：

步骤1利用概率密度原理，中核函数K(·)演变思想，通过对核密度采样来实现对整个连续近似分布的采样，生成新粒子集及对应权值中：NReg 为连续近似分布中采样粒子个数，表示k 时刻第j 个新粒子的目标方位角，表示k 时刻第j 个新粒子的权值；是对核密度进行重新标度的核密度。

最佳核密度函数是Epanechnikov 核密度，表示为：

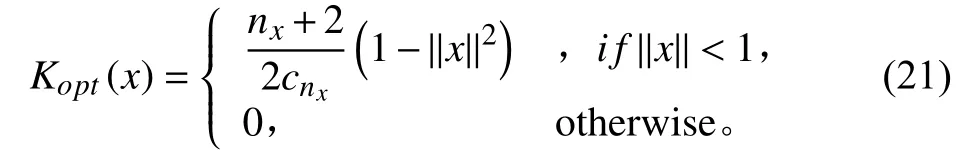
式中： cnx为为 Rnx内单位超球体的体积； nx为状态量的维度。

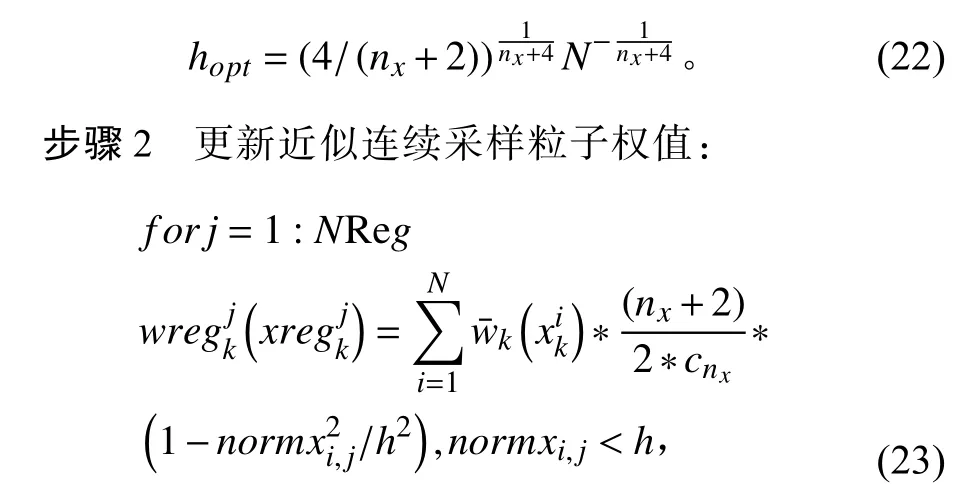
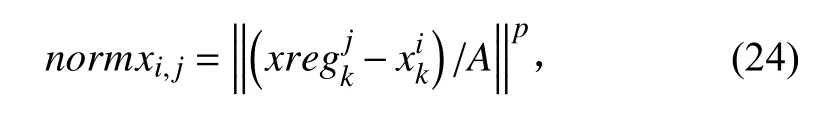
其中A 表示粒子状态协方差矩阵S 经过Cholesky 分解得到的上三角矩阵，若取p=1，表示L1 范数正则化；若取p=2，表示L2 范数正则化。

步骤3计算正则化粒子权值归一化：

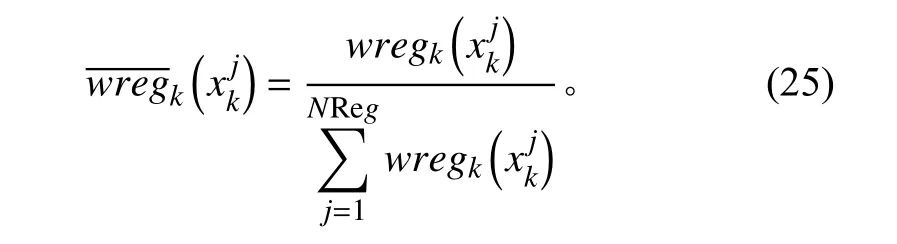
4 仿真研究

为了验证所提出L2-RPF 算法的有效性，针对水下目标运动单站纯方位角跟踪这一典型非线性系统进行Monte Carlo 仿真分析，并将L1-RPF 与PF 算法在仿真初始条件相同情况下进行性能对比。

本实验考虑远场平面波模型，假设观测站与跟踪目标处于同一水平面上，且深度信息已知，采用地理坐标系，取正北方向为0°，只考虑x 和y 两个方向的坐标。假设观测平台作匀速直线运动，目标作匀速和匀加速交替运动，在不同时间段观测平台和目标具体的运动状态设置如表1 所示，观测时间间隔为1 s，观测总时长为110 s，观测平台初始状态向量为Bx0=[-150,700,3,3,0,0]T，目标初始状态向量为X0=[5,3,5,2,0,0]T，过程噪声协方差为Q=diag[1,1.3,0.4,0.1,0.01,0.01]，初始协方差矩阵为P0=diag[1,1,0.1,0.1,0.01,0.01]，观测平台和目标轨迹如图1 所示。

表 1 目标及平台运动状态Tab. 1 The movement status of target and platform

PF 算法粒子数N=100，L1-RPF 与L2-RPF 算法正则化粒子数NReg=5*N，粒子采样子空间半径为Net=1。采用3 种算法对水下目标进行方位跟踪，跟踪曲线图2 所示。

分析可知，L1-RPF 算法估计的目标方位与真实方位基本保持一致，L2-PRF 算法次之，PF 算法随着时间推移，滤波发散，估计方位与真实值偏离较大。

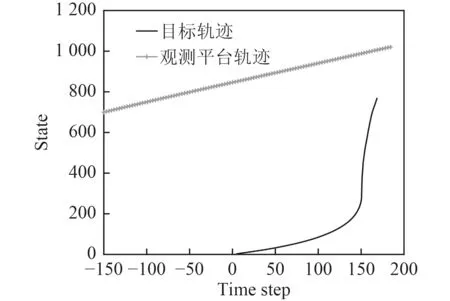
图 1 目标及平台轨迹图Fig. 1The diagram of target and platform trajectory

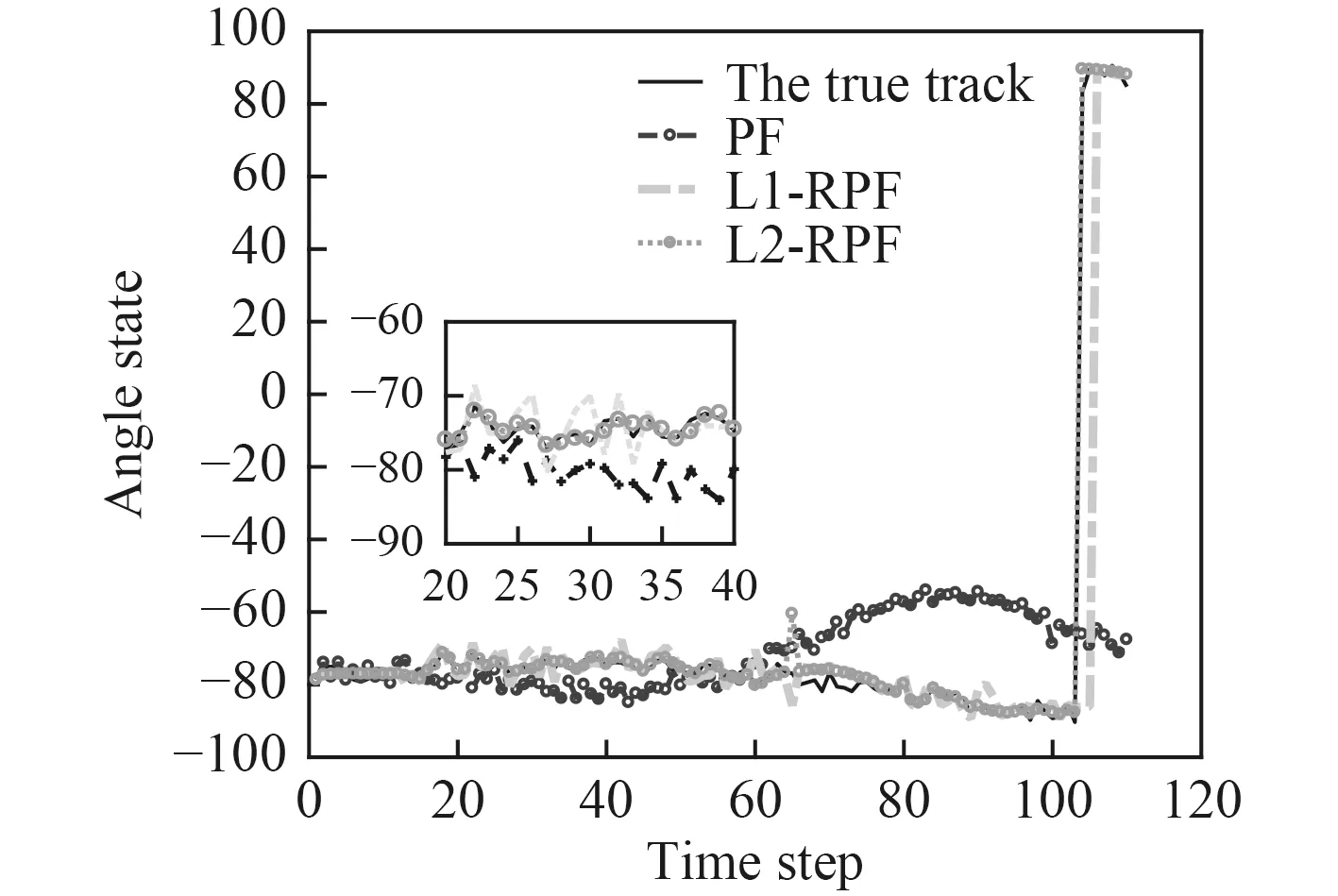
图 2 PF，L1-RPF，L2-RPF 方位跟踪Fig. 2The bearing tracking of PF, L1-RPF, L2-RPF

为了进一步定量分析L1-RPF，L2-RPF 与PF 算法在此种工况系统下的方位跟踪误差，基于上述初始条件，将3 种算法进行50 次Monte Carlo 仿真实验对比，选用平均误差ME 和均方根误差RMSE 来衡量误差大小，其中ME 为多次Monte Carlo 实验对应每个时刻目标方位估计值与真值绝对误差的均值，表示为：

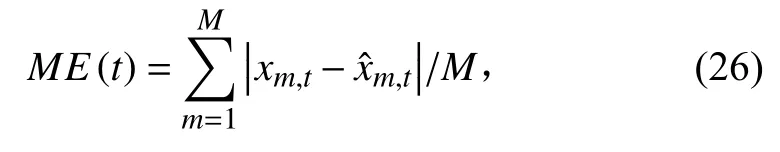
RMSE 为观测值与真值偏差的平方和与实验次数M 比值的平方根，表示为：

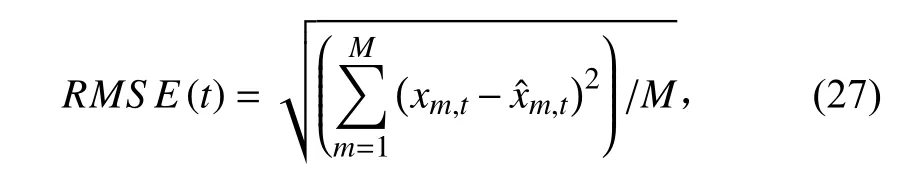
其中，M 表示Monte Carlo 实验次数，xm,t表示第m 次实验t 时刻方位真值，表示第m 次实验t 时刻估计值。

得到观测时间内的跟踪误差曲线图如图3 和图4所示。

通过对比分析可以得到：

1）相同的初始仿真条件下，L2-RPF 算法的ME和RMSE 误差小于L1-RPF 小于PF，相较于L1-RPF 算法和PF 算法，L2-RPF 算法跟踪精度更高些；曲线抖动小，也说明该算法鲁棒性更好些；

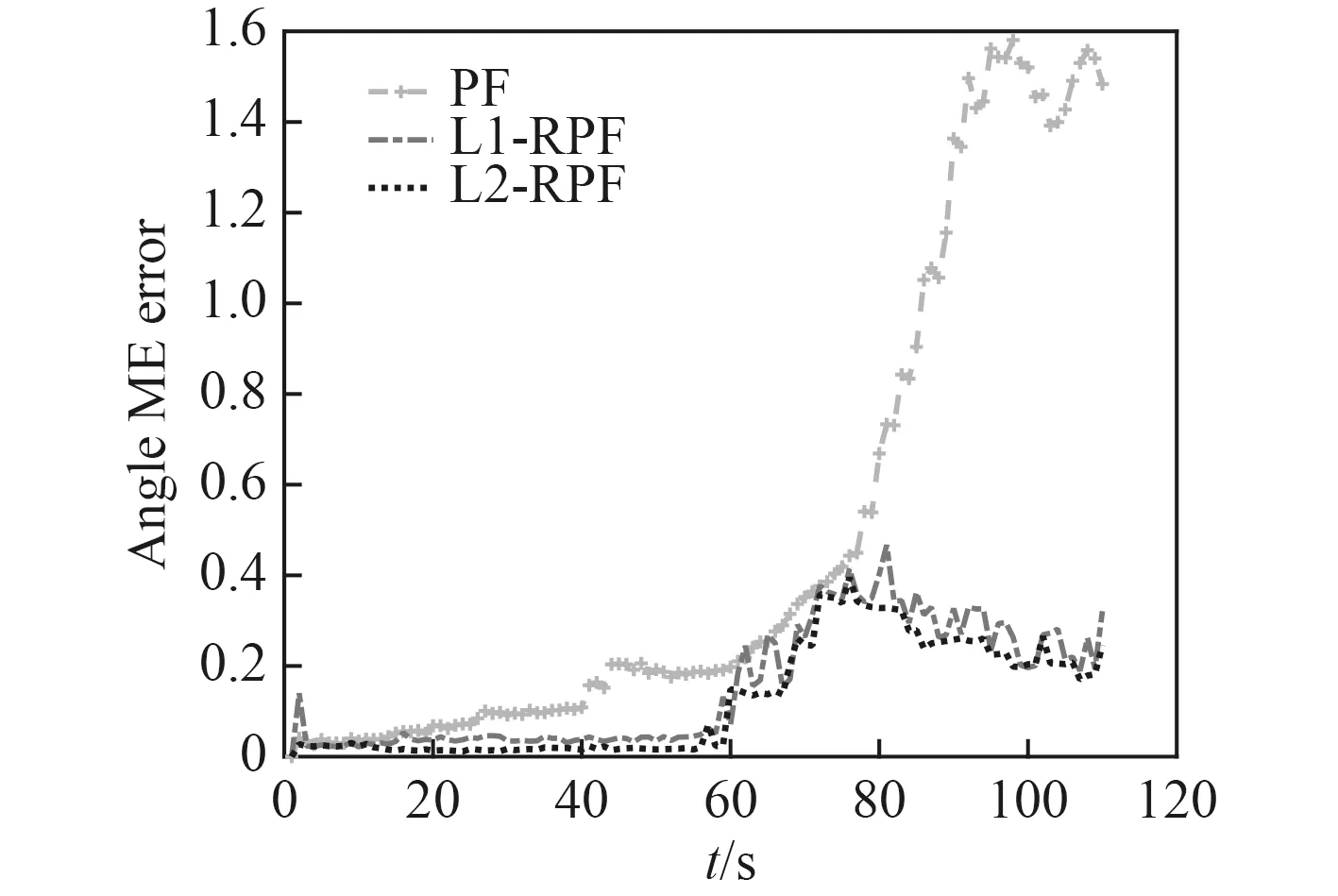
图 3 ME errorFig. 3ME error

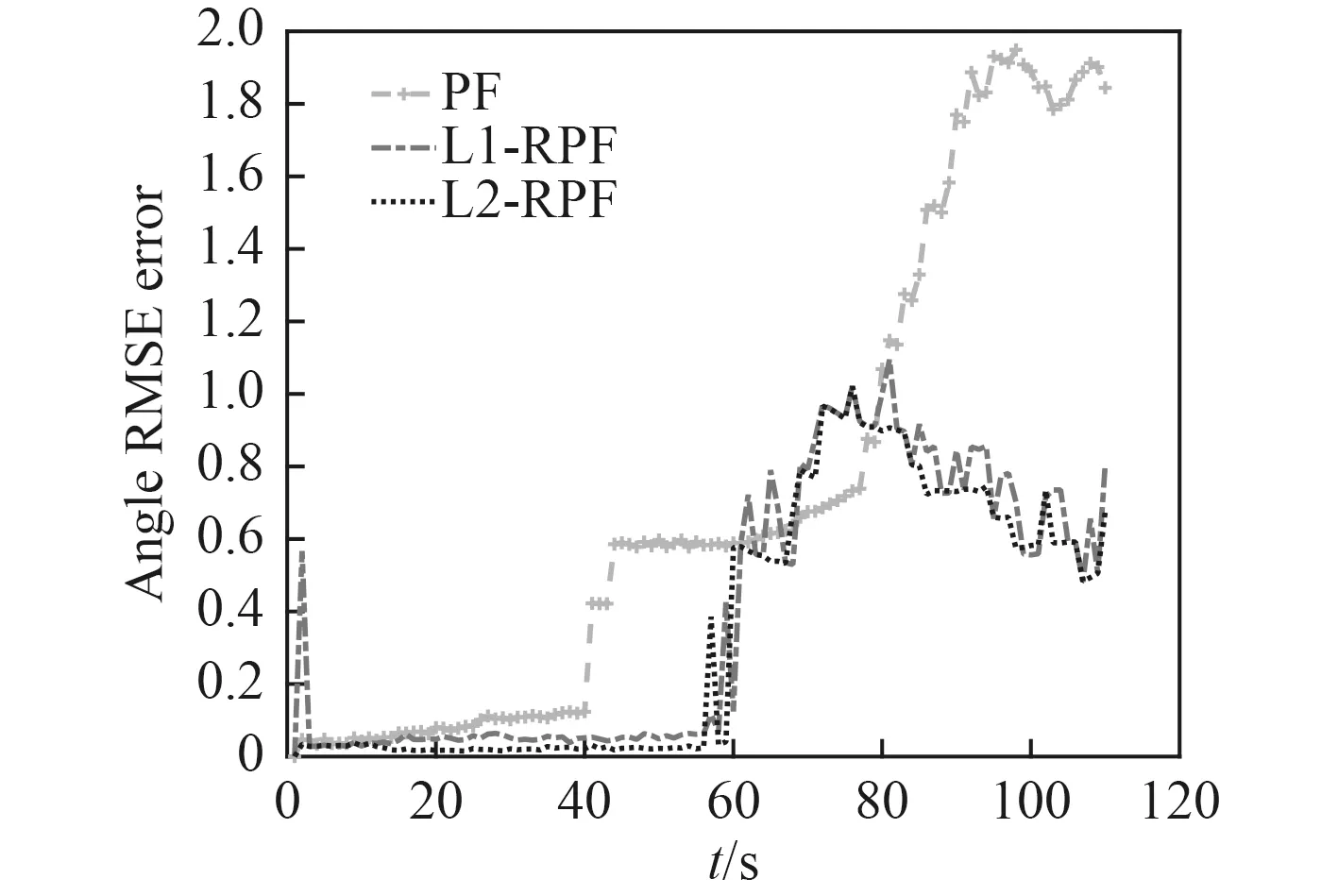
图 4 RMSE errorFig. 4RMSE error

2）随着时间推移，3 种算法的跟踪误差有不同程度变大，L2-RPF 跟踪误差小于L1-RPF 小于PF。PF 算法由于粒子贫化，滤波发散，导致跟踪误差变大；L2-RPF 算法跟踪平均误差在0.5°以内，均方根误差在1°以内，相对较小。

5 海试数据处理与分析

利用在南海北部海域开展的水下声学滑翔机平台探测跟踪性能验证试验数据，针对水下移动观测平台在海上对水下目标采用PF，L1-RPF，L2-RPF 三种算法的纯方位角跟踪性能。

试验海区深度约为1 500 m，试验期间气象水文条件良好，风级约为2 级，XCTD 测量结果显示，声速剖面在深度40 m 以内是均匀层，深度40～200 m 范围内为声速主越变层，声道轴在1 000 m 附近深度上。试验中，水下声学滑翔机在10:55 以24°俯仰角下潜向下在水下做剖面滑翔探测跟踪目标，滑翔速度为1 kn，一个剖面时长大约4 h。在12:52～13:49 时间段内，1 艘船长42 m，船宽6 m，航速8.4 kn 的水面航船以301°航向与水下声学滑翔机滑翔轨迹垂直而过，水下滑翔机与水面航船的态势图如图5 所示。

采用PF，L1-RPF，L2-RPF 算法处理试验数据，并根据水下声学滑翔机推算位置和水面目标GPS 位置得到近似真实的方位，结果如图6 所示。分析可知，通过复声强器法得到的初始滤波结果，存在野点，且跟踪精度不高，对比几种算法和GPS 推算方位，L2-RPF算法和L1-RPF 算法要比PF 算法目标方位跟踪精度相对较高，PF 算法由于粒子贫化，导致滤波器发散，影响收敛时间和估计精度。但由于RPF 算法是在测量值和估计值之间的均衡，测量值出现野点也会影响RPF 算法的方位跟踪结果。从图6 细节处可以看到，受野点的影响，RPF 算法也出现抖动，跟踪效果稍差，分析这是滤波因子选取不当引起的滤波效果变差。

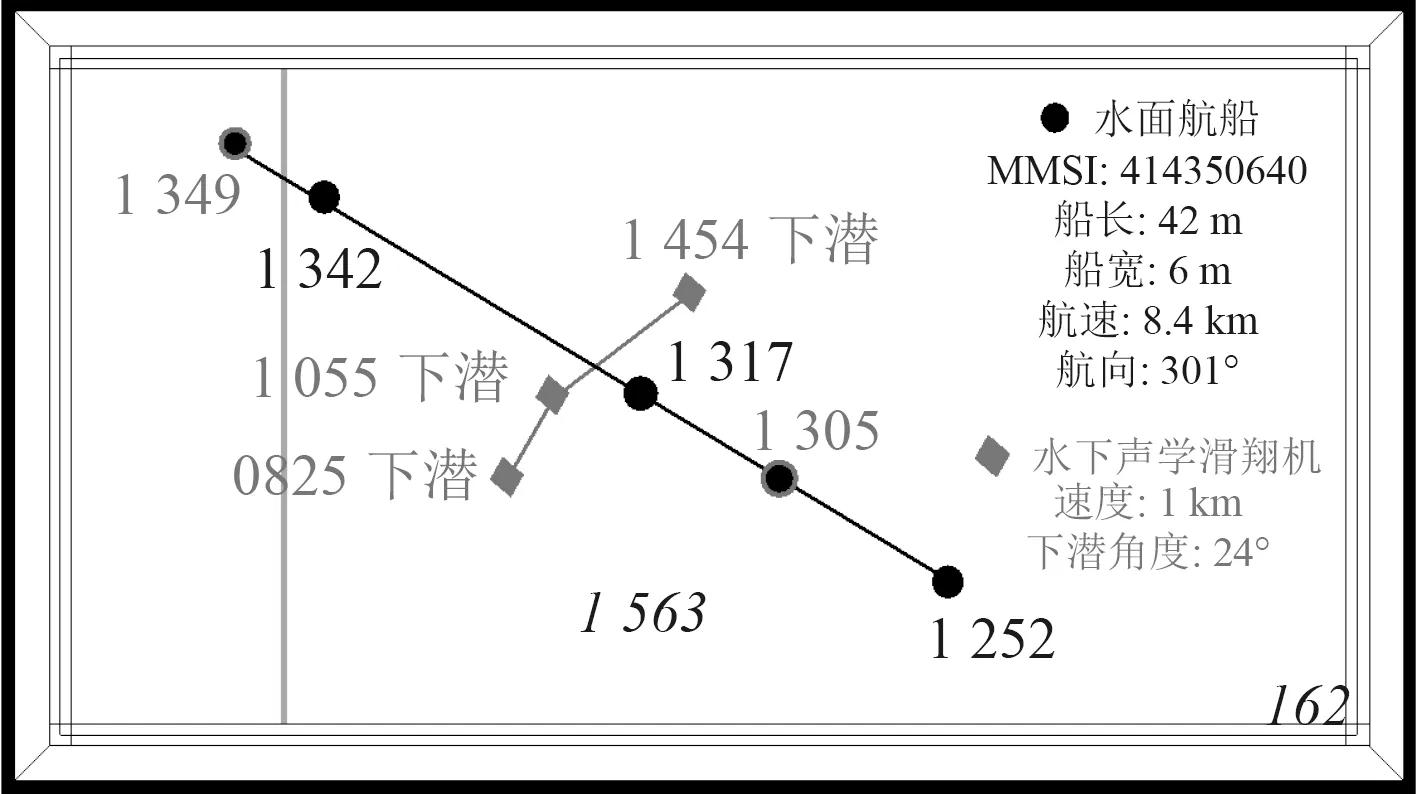
图 5 水下平台与目标位置态势图Fig. 5Situation map of underwater platform and target positon

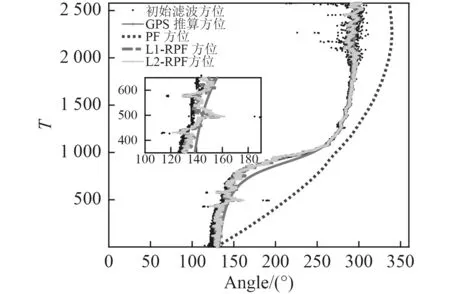
图 6 PF，L1-RPF，L2-RPF 算法目标方位跟踪结果Fig. 6Target bearing tracking result of PF, L1-RPF, L2-RPF

6 语 结

本文所述针对水下声学滑翔机对水下目标进行纯方位角跟踪的实际应用，采用PF，L1-RPF，L2-RPF 算法，理论仿真和试验表明，L2-RPF 算法相较于其他粒子滤波算法，改善了粒子贫化，提高了目标跟踪精度。L2-RPF 算法在水下声学滑翔机目标探测跟踪上的应用，为多水下无人平台多目标的探测跟踪奠定了基础，对于水下无人平台组网探测跟踪水下目标有较好的应用前景。