促进学生数学核心素养发展的教学实践

赵方超

摘要：培养发展学生的核心素养是初中数学的目标，在教学中自然的渗透、和谐的培养学生这些方面的能力，对每位老师而言都是需要实践、思考的问题。下面以“一次函数的应用“为例，探讨。

关键词：核心素养;自然;实践

一、问题提出

比较平时课堂与公开课，公开课由于精心准备、上课过程紧凑、精准、课堂活跃，对于新课程标准要求培养的学生数学核心素养，完成的十分出色，而平时课堂稍显平淡，对于核心素养的培养没详细的方案，略显不足，因此希望找到一种教学方法，能够平衡两方面，在上一次函数的应用时探索了一下。

二、教学中的实践探索

这节课讲一次函数与行程，涉及到多个知识点的协同，涉及数形结合、函数思想等数学方法，与多个数学核心素养，如运算能力、推理能力、模型思想有着密切联系。

这节课结合一题一课的思想，通过把问题从简单到复杂的改变，让学生逐步建立思考模式，能够主动的、深入的思考，老师起到引导和解惑的作用。

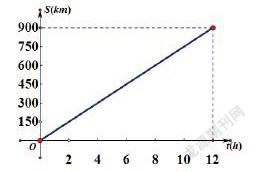
新课引入：一列慢车从甲地匀速驶往乙地，12小时后到达乙地。图中的线段表示慢车行驶的路程S1（km）与慢车行驶的时间t（h）之间的函数关系。根据图中的数据确定函数关系式    。

（1）学生审题

审题时，以启发引导的发问为主，以便让学生理解题目，例如，这个图象表明了什么？为什么图象是线段？有没有特殊的点，它的含义是什么？把题目从图象转化学生脑海中一个生动的形象。

（2）逐步深入、小组讨论

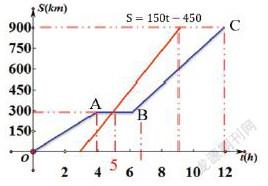
一列慢车从甲地匀速驶往乙地，12小时后到达乙地。图中的线段表示慢车行驶的路程S1（km）与慢车行驶的时间t（h）之间的函数关系。一列快车也从甲地匀速驶往乙地，比慢车晚出发3小时，比慢车早到了3小时。

①试在（1）的坐标系中画出快车行驶的路程S2（km）与慢车行驶的时间t（h）之间的函数关系图像

②根据图像，求出S2与t的关系式。

当问题变得复杂，引入第二列火车，给学生多一点时间，让学生2人一组或4人一组讨论，让学生自己多尝试，培养学生的推理能力和数据分析观念。分组讨论有利于引发学生思维的火花，大大加强了学生的课堂参与度，贴合以学生为中心的新课标理念。

学生经过讨论与尝试，能够画出快车的行驶路线，同时能够利用待定系数法求得解析式：S2=150t-450

（3）自主改编，主动参与

学生解答完上述题目之后，引导学生思考图象交点的意义，交点坐标要如何求解？还是采用启发发问，为什么会有交点？交点的横纵坐标的现实意义是什么？学生经过讨论得到交点（6，450）表示列车的追及点，表示离出发点450km的地方相遇。

当学生回答完问题时可以请不同的学生来提出新的问题，让学生主动进行改编，引导规范学生在大框架不变的情况下，发散性思维，或者与实际结合，贴近现实生活来改编。

一位学生提出：一列货车从相距900千米的甲地驶往乙地，速度为75km/h，行驶4小时后到达丙地，停留2小时后加速开往乙地。图中的线段表示货车行驶的路程S1（km）与货车行驶的时间t（h）之间的函数关系。一列快车也从甲地匀速驶往乙地，比货车晚出发3小时，比货车早到了3小时。在快车出发几小时后追上货车？

这个问题比较切合实际，我帮助学生完善了题目的细节，把学生的描述抽象成这样一个问题。面对这样一个问题，由于之前的铺垫，虽然题目有难度，但学生都乐于思考，想要解决它。解决这个问题的方法有多种，让学生暢所欲言，占主体地位，教师起辅助作用。学生的想法有：①分时间段来考虑、②方程思想、③画行程图，利用追及问题的公式，这些想法都可行，也体现了学生对之前所学知识的掌握，虽然和本节课的主题不符，还是要鼓励为主。学生讲了这三种方法的解答过程，比较它们的优缺点，然后引导学生与本节课的例题结合，采用一次函数的方法来解决这一问题，画出两列车的图象，发现交点在货车停留的那一段时间，然后利用待定系数法求出解析式解决了这个难题。

三、总结

经过这一堂课的准备、上课、反思，基本达成了我想要的目标：在教学中自然的渗透数学核心素养的方法。我把这个方法归纳成五步：（i）贴合实际引入（ii）师生共审题（iii）小组讨论（iv）自主改编（v）总结思考，当然可以根据不同的课题或增或减步骤，特别要注意的是这个方法需要教师有很多的耐心引导鼓励学生、有广博的知识面、有与学生共同成长的心态、有终身学习的理念。这个方法的以启发教育为主，贴近现实生活为辅，结合小组讨论、自主思考等手段，让整个学习过程既有乐趣，靠近现实社会，又不失严谨，不失数学本质。

参考文献：

[1]邵朝友，周文叶，崔允漷.基于核心素养的课程标准研制：国际经验与启示[J].全球教育展望，2015，44（08）：14-22+30.