基于小波包和支持向量机的滚动轴承故障诊断

涂志松

（福建省特种设备检验研究院漳州分院，福建漳州 363000）

0 引言

滚动轴承是机械设备的重要旋转部件，对机械设备安全运行起着十分重要的作用。滚动轴承故障是机械设备的重要故障源之一，在旋转机械的故障中，有约30%的故障是因滚动轴承故障而导致的[1]。因此，滚动轴承故障诊断，特别是早期微弱故障的诊断，具有非常重要的实际意义。

最实用的滚动轴承故障诊断方法是使用振动加速度传感器获取滚动轴承的振动数据、对数据进行处理，最终分析判断滚动轴承的故障类型[1]。振动加速度传感器采集的信号存在大量的噪声和干扰，提取能体现滚动轴承运行状态的数据是十分困难的[2]。当滚动轴承发生故障时，故障部位会与轴承部件产生一定频率的碰撞，从而产生一系列的振动，这些振动信号具有非平稳特征。滚动轴承制造装配的误差会使碰撞不连续，导致故障频率在一个范围内波动[3]。目前，常见的信号处理方法不能很好地提取出反应滚动轴承运行状态的特征信息[4-6]。小波包变换是以小波变换为基础发展而来的，含有高通滤波器和低通滤波器，在高低频段都具有高的频率分辨率。特别是在高频段，小波包变换比小波变换具有更高的分辨率。对于各种各样的信号，小波包变换具有很好的适应性，但也增加计算的复杂性。小波包变换可应用于滚动轴承非平稳信号的降噪和时频分解[7-8]。基于此，本文构建基于小波包变换和支持向量机的故障诊断系统。对振动信号进行小波包变换，求关键部分频带的能量值，构造归一化能量特征向量，应用特征向量对支持向量机进行分类识别训练，构建故障诊断系统。用此系统对滚动轴承的振动数据进行分类识别。结果表明，该模型可有效识别滚动轴承的故障类型。

1 基本理论

1.1 小波包分解

对于平稳信号和非平稳信号，连续小波变换被认为是有效的信号处理工具。但是，其包含很多冗余的信号，而且计算量非常大、计算效率很低。因此，Mallat 基于共轭二次滤波器设计出离散小波变换算法。在不同尺度下，小波函数和尺度函数是单尺度函数φ（t）在双尺度差分方程中产生的：

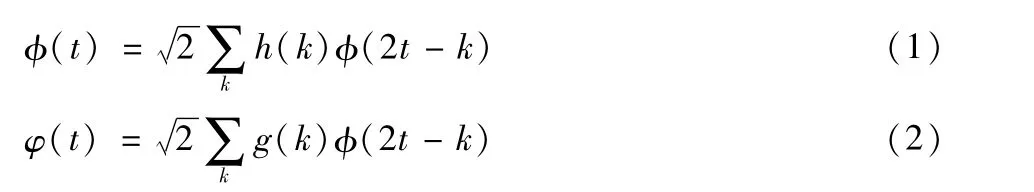
式中：g（k）＝（-1）kh（1-k），h（k）和g（k）分别为低通、高通滤波器的滤波系数；φ（t）和φ（t）分别为尺度函数和小波函数。

在正交小波变换中，不同尺度下，一系列递归计算产生尺度系数和小波系数：

式中：cj，k、dj，k分别为尺度系数和小波系数，是由信号投射到尺度函数φj，k（t）和小波函数φj，k（t）上得到的。

因为小波分解对高频部分不再进一步分解，导致有用信息丢失。为了对高频部分进行分析，需要提高采样的频率，这便产生了小波包分解。

小波包分解是使高低频率成分通过滤波器进行分离，将信号通过高通和低通滤波器进行滤波，得到信号的细节部分（高频段）和宏观部分（低频段），然后，对高频段和低频段进一步分解，分别可得到在高、低频段下一层次上的低频段和高频段，数据长度均为原数据长度的一半。

设f（t）为信号，为2j尺度上的第i个小波包，即节点（j，i），则小波包分解算法为：

式中：t＝1，2，…，2J-j；i＝1，2，…，2j；J＝log2N。

H（t）和G（t）为正交镜像滤波器，H（t）与尺度函数φj（t）有关，为低通滤波器；G（t）与小波函数φj（t）有关，为高通滤波器。

小波包重构算法为：

式中：j＝J -1，J -2，…，1，0；i＝2j，2j-1，…，2，1；J＝log2N。

图1 小波包分解原理图

小波包分解可以把信号按任意时频分辨率无泄漏、不重叠地分解到不同频段中。信号通过小波包分解后，信号所有信息都得到保留。这种分解可以按照需要进行多次，最终获得所需要的频率。图1 所示为对一个信号进行3层正交小波包分解的原理图。将原始信号记为A，小波包分解经过滤波器H 和G 后可以获得第1 层2 个子频带A10与A11；对第1层的2个子分量分别进行分解，可以获得第2层的4个子频带A20、A21、A22 和A23；以此类推，又可以获得第3层的子频带。

1.2 小波包能量特征向量

滚动轴承振动信号小波包分解的波形是很复杂的，直接应用小波包分解波形进行故障诊断是困难的。小波包分解后，频域的能量分布在故障诊断中起着巨大的作用。不同的运行状态中，滚动轴承振动信号在频域中的能量分布是不相同的。频域中的能量分布作为信号特征可以有效标识滚动轴承的运行状态。小波包分解中提取频率段的能量值称为小波包能量谱。信号在小波包分解前后的总能量是相等、没有泄漏的。用小波包能量谱描述原始信号的能量分布是可靠和精确的[7-8]。

对某一层次小波包分解，信号在该层次的能量E（j，n）定义如下：

假设对原始信号s（t）进行了J层小波包分解，则在第J层上信号s（t）的小波包能量特征向量表示如下：

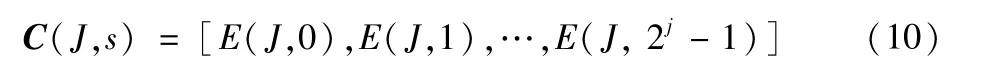
同一运行状态中，不同频段的能量值差异悬殊，为能对能量特征进行分析处理，需要对上述构造的特征向量进行归一化处理。

令：

则归一化特征向量为：

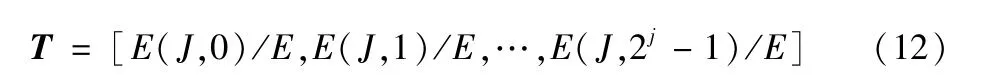
1.3 支持向量机基本理论

有些重要关键设备要求故障率极低，此时，故障状态数据样本不足，利用传统的智能诊断技术往往由于缺少故障样本数据而得不到理想的诊断效果。支持向量机仅需要正常运行状态的数据样本和少量故障状态数据样本，就可以识别出设备的运行状况，很好地解决了故障诊断缺少故障数据样本的问题，具有重要的实际应用价值[9-13]。

图2 线性可分超平面

支持向量机主要思想是创建一个超平面作为决策平面，能正确地分类出所有的训练样本数据，训练样本中离分类界面的最近数据样本与分类界面的距离值取最大。在线性分类二维空间中，超平面几何图形如图2 所示。五角星和矩形对应二类样本，P为分类直线，直线P1和P2为距离分类直线的最近样本，平行于分类直线。直线P1和P2的距离是分类间距。直线P1和P2上的样本就是支持向量机。

假设训练样本是：

式中：ω为可变的权重向量；x 为特征向量；b为补偿值。支持向量机的目标是使P1和P2间隔最大化：

约束条件：yi（ωTxi+ b）≥1i＝1，2，…，m

为了解决该问题，引入拉格朗日乘数，将约束条件问题转化为对偶问题：

最终可得到最优分类函数：

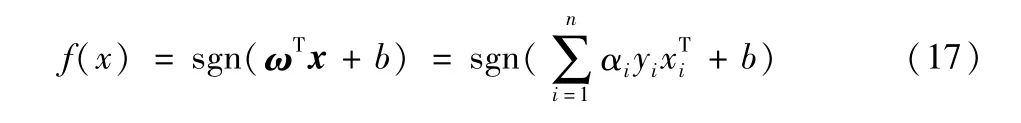
对于线性不可分问题，通过非线性映射函数，将样本映射到高维特征空间，在高维特征空间中，构建最优分类函数，将线性不可分问题转化为线性可分问题。非线性映射函数即为核函数。通过适合的内积核函数K（xi，x），将低维空间数据映射到高维空间中，在高维空间中，进行线性分类，这个过程并不增加计算的复杂性。与线性可分相比，约束条件变成：

式中：参数c为对错误分类的惩罚因子，用于控制错误分类的程度。

最优分类函数变为：

本文使用高斯径向基核函数：

不同的机械设备，使用不同的核函数，模式识别的准确率是不同的。对于滚动轴承振动数据，使用高斯径向基核函数时，具有较高的分类准确率[14]。因此，本文采用高斯径向基核函数模型对滚动轴承振动数据进行分类识别。

本文使用支持向量机的多值分类算法，如图3 所示。其基本思想是：针对M类分类问题构造M个二类分类器，其中每个分类器负责识别出某一类样本数据。这样M个二类分类器，可识别出M类样本数据。分类时，将未知数据分别依次输入M个分类器中，比较这些分类器的函数值，就可判断未知数据的类别。

图3 多值分类算法

2 滚动轴承故障诊断

滚动轴承的故障诊断主要部分包括振动数据特征提取和模式识别。将正常工况的振动数据、已知故障工况的振动数据作为标准数据，识别时，通过数据分析处理，将待识别的振动数据与正常、故障工况的数据进行比较，判定滚动轴承正常与否、故障的类型。

2.1 振动信号特征提取

信号在频域的能量分布体现滚动轴承运行状态。运行状况不同，频带能量分布情况也不同。滚动轴承发生故障后，会使得某些频带内的能量增加，另一些频带内的能量减小。可将频段能量构造为故障诊断系统的特征向量。

图4 滚动轴承振动信号小波包特征提取

综合对比不同运行状态下的频域能量值分布特性，选择对振动数据进行4 层小波包分解，得到分布在16 个频带的数据，计算16个频带的能量值，构造特征向量，对向量进行归一化处理，从而构造出不同运行状态下的关键特征向量标准库，该过程如图4 所示。从正常运行的滚动轴承数据中提取4 096 个数据采样点，对其进行特征提取，其时域波形、归一化特征向量如图5～6所示。

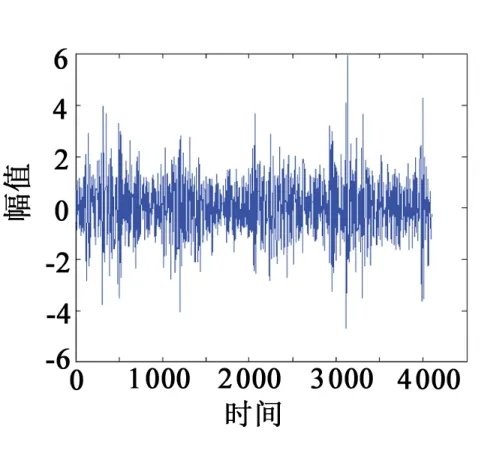
图5 正常滚动轴承振动波形图

图6 正常滚动轴承能量直方图

2.2 训练分类模型

对支持向量机故障诊断系统进行训练：已知滚动轴承的运行状态，对此时测得的振动数据进行小波包能量特征向量提取，并作为故障诊断系统的输入数据。用数值标识运行状态，比如0 为正常运行，1 为故障运行。将该数值作为故障诊断系统的输出数据。训练分类模型如图7所示。

图7 训练分类模型

2.3 故障诊断

应用振动传感器实时采集振动数据，按以上3 个步骤，构造出对应的能量特征向量。将特征向量作为步骤3 中分类模型的输入数据，故障诊断系统的输出数值，标识滚动轴承的运行状态。滚动轴承的故障诊断过程如图8所示。

图8 故障诊断

2.4 实验分析

将本文所研究算法应用于滚动轴承的故障诊断中，以验证其有效性。所有算法使用MATLAB软件实现。采用的轴承数据来源于XJTU-SY滚动轴承加速寿命试验数据，试验平台如图9所示。该实验对象为LDK UER204 滚动轴承，在水平和竖直方向，使用振动加速度传感器采集轴承的振动信号，采样频率为25.6 kHz，每次采样时长为1.28 s，采样间隔为1 min。轴承的转速为2 250 r／min，所受径向力为11 kN，测试轴承的详细信息如表1所示。

图9 轴承加速寿命试验台

表1 XJTU-SY 轴承数据集信息一览表

本实验一共选取4 类运行状态的数据（包括正常、保持架故障、外圈故障和内圈故障）。设计4个二类分类器，每个分类器可诊断出一种运行状态，SVM1 用于识别正常滚动轴承，SVM2用于识别保持架故障，SVM3 用于识别外圈故障，SVM4用于识别内圈故障。针对分类器，将其要识别的运行状态对应的系统输出设为1，其余运行状态的系统输出设为0，由此设计训练4 个二类分类器。SVM 故障诊断系统的分类如表2所示。

表2 SVM分类

对振动数据进行小波包分解：T＝wpdec（x，4，'db2'，shannon），振动数据向量x 在小波基db2 的4 层小波包分解，shannon为熵标准，wpdec函数返回值为小波包树。得到16个子频带分别为：（0～800 Hz），（800～1 600 Hz），（1 600～3 200 Hz），…，（12 000～12 800 Hz）。支持向量机选用高斯径向基核函数，C取96，g取8.333 时，故障诊断系统的分类正确率较高，能很好地识别出滚动轴承的运行工况。

将测得的数据分为偶数组和奇数组，偶数组数据作为训练样本数据，训练故障诊断系统。奇数组数据作为测试数据，使用故障诊断系统对其进行分类识别。从实验结果（表3）可看出，4种运行状态的分类识别率都较高，故障诊断模型是有效的。

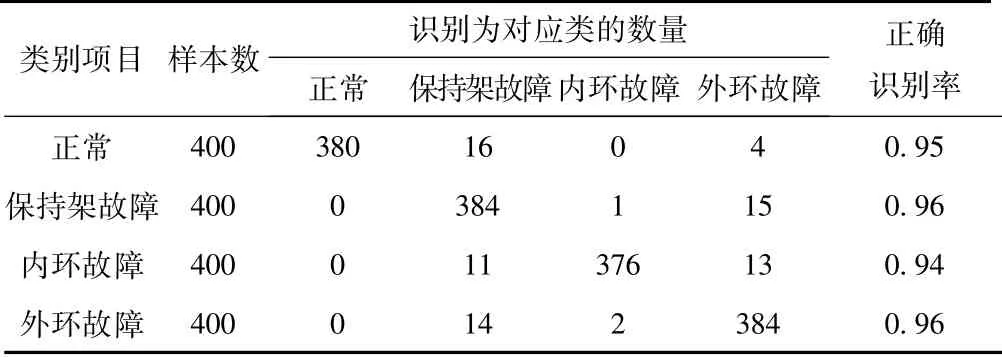
表3 分类识别结果

3 结束语

针对滚动轴承振动信号非平稳特性和故障样本不足的问题，本文结合小波包多分辨率，可以实现更精细化分解的特性，以及支持向量机少数支持向量决定最终结果的特点，提出一种基于小波包能量和支持向量机的滚动轴承故障诊断方法。实验结果表明：

（1）小波包分解能够有效地对非平稳信号进行不同频带的精细分解，便于选取相应的子频带，为提取特征信息提供强有力的支持，构造能量特征向量，减少故障诊断系统的样本数据量，提高了计算效率；

（2）支持向量机，只需少量的训练样本数据就能实现正确分类，具有算法简单、计算效率高和分类正确率高的优点；

（3）本文所提方法简单高效，满足滚动轴承故障诊断的技术特性要求。

本文提出的故障诊断模型，达到较好的效果，但仍存在一些问题需要进一步研究。实验是针对3种单一故障进行的，但是滚动轴承故障类型很多，而且是多种故障复合出现的，其特征提取更复杂、分类识别难度更大，因此对于复合型故障还有待进一步研究。