第三系富水粉细砂岩地层基坑冻结加固研究
2021-01-18尹陇娟
向 亮,尹陇娟
(中铁第一勘察设计院集团有限公司,西安 710043)
引言
随着我国城市化的快速推进,城市拥堵问题日益严峻。城市轨道技术具有运量大,速度快的优点,对于解决拥堵问题和提升公共交通服务水平有着重要的意义[1-2]。多数地铁隧道需穿越城市中心地区、建筑物密集区,有的也位于江河下方,或穿越软土、富水砂层等特殊地层。在复杂地层条件下,城市轨道技术中的地铁车站开挖常采用人工冻结技术进行止水加固,对人工冻结施工时产生的温度场的变化以及冻胀对周边构筑物、管线的影响仍需进一步研究[3]。
人工冻结法施工占用地面面积小,容易将冻结和开挖引起的地表沉降控制在规范要求之内,具有对周围环境影响小,不影响交通的优点[4]。冻结法早期运用于矿井工程,近些年随着城市地下空间的扩展,采用冻结施工的防水、支护等功能越来越多的运用于城市地铁、基坑、隧道、人防等工程中[5]。从70年代开始,国内学者对人工冻结法进行了大量研究,陆续将人工冻结法运用于地铁隧道工程[6-10]。陈湘生等对人工冻土的力学性质进行分析[11-12];胡向东等对多种情况下人工冻结施工中温度场与冻结帷幕进行了研究[13-14];何川、晏启祥等进行了复杂工况下冻结法在地铁联络通道的力学研究,考虑了地层冻结的水、热、力三场耦合优化冻结法设计[15];蔡海兵等开展了冻结施工对地层与地表的融沉影响模型试验研究[16-18],卢亦焱[19]对港珠澳大桥珠海连接线拱北隧道管幕冻结过程进行了有限元数值模拟,分析了冻结管布置圈整体温度场及冻结帷幕厚度随时间的变化规律;孙冠东[20]分析了人工冻结在岩土工程中的应用现状及发展,提出冻结帷幕厚度的确定及冻胀融沉给工程带来的影响是二者共同的核心问题。
兰州地铁1号线是国内首次在第三系富水粉细砂岩地层中修建地铁暗挖工程,也是首次在兰州第三系富水粉细砂岩地层进行冻结施工。以兰州市地铁1号线省政府车站基坑开挖为例,通过参数分析、监控数据、关键施工技术研究等方面,介绍冻结法在车站基坑工程中的应用,并对关键数据进行监测分析,希望能对类似工程提供一定借鉴。
1 工程概况
省政府车站段为兰州地铁1号线的控制工程,全长为170.75 m,标准段宽22.9 m,结构底部埋深30 m。车站位于城关区张掖路与酒泉路十字东南象限地块内,周边建筑物密度大,建筑物级别高:车站北侧为甘肃省人民政府,西侧为农业银行办公楼,东侧中环广场高层建筑距车站最近为7.9 m,车站穿越中央商务区(已拆除)与农业银行裙楼且其周边存在电缆槽、污水管道等管线。
车站基坑分为两个部分:省政府端基坑长70.84 m,基坑宽度23.5 m,采用连续墙+钢筋混凝土内支撑支护,中央商务区端基坑与中央商务区结合,长99.91 m,车站基坑标准段宽度23.1 m,车站大里程扩大端基坑宽度26.6 m,采用连续墙+钢管内支撑系统支护,两个基坑间采用咬合桩分隔。
特殊地质为第三系富水粉细砂岩,其成岩作用差,但原岩一般含水率不高,在4%~6%,结构紧密,直立性较好。当地下水含水率升高时,此类砂岩经开挖扰动、受水浸润或浸泡后,围岩软化现象明显,尤其是在地下水富集地段,将会出现涌水、涌砂现象。施工扰动后多呈粉细砂状,软化,地表变形现象很严重,对于车站、联络通道、周边建筑物及管线安全性有很大隐患,所以基坑的防水处理是重大难题。
2 人工冻结设计
面对富水第三系粉细砂岩特殊地层深大基坑,基坑内出现漏水,并导致大面积流沙现象(图1)。若不在基坑开挖中做好防水措施,第三系粉细砂岩将会迅速失去强度,轻则形成孔洞导致基坑涌水涌砂,严重时基坑四周建筑会产生不均匀沉降,甚至基坑倒塌。由于之前在其他区段施工中使用的一般降水和防水方法的效果都不够理想,而相邻区段的联络通道冻结施工都相继取得了初步成功,因此,最终决定在咬合桩周边进行局部人工冻结,以达到加固止水的目的。

图1 基坑内砂岩软化现象
本工程局部人工冻结加固的方式是,采用人工制冷方法对基坑地下连续墙与咬合桩间的土层降温冻结,形成一个封闭的冻土帷幕结构,由于冻土帷幕的存在隔绝了侧向地下水影响,后续的基坑开挖构筑难度也随之降低。基坑支护与冻结加固方案如图2所示。

图2 基坑支护与冻结加固方案
2.1 冻结法适用性分析
2.1.1 单管冻结温度场
为研究冻结法施工在第三系富水粉细砂岩中的适用性,可从该地层单管冻结效果入手。由于冻结管的半径远小于其长度,可将其作为平面内冷源的热传导问题进行研究。在计算分析之前先做如下假设。
(1)冻结管的温度辐射仅发生在垂直于轴线方向。
(2)平面内某点的温度不仅与其坐标位置有关,也与冻结时间相关。
(3)待冻土体均质连续,且具有同一初始冻结温度。
(4)无穷远处的温度为地层初始温度。
(5)不计相变发生的时间,当某点达到冻结温度时,即可认为该位置土体已经冻结。
因此,平面内某一点的温度可以用函数T(r,t)表示,其中r为任意点与热源之间的距离;t为时间。
如图3所示,以冻结管位置为中心,由内到外将平面分为冻结区Ⅰ与未冻区Ⅱ两部分。

图3 单管冻结计算模型
由于冻土与未冻土的热物理参数不同,因此热传导方程分开表示

(1)

(2)
式中,T1、T2分别为冻结区和未冻区温度,℃;t为冻结时间,s;a1、a2为导温系数,m2/s,a=λ/c;λ为导热系数,kJ/(m·s·℃);c为体积比热,kJ/(m3·℃);r为任意点距离冻结管中心的距离,m;r0为冻结管半径,m;R为冻结锋面半径,m。
冻结管外表面的热交换可表示为
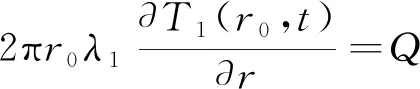
(3)
式中,Q为冻结管外表面吸收的热量,kJ/(m·s)。
由假设条件,冻结开始之前地层温度恒定(以T0表示),无穷远处的土体温度依然为初始温度T0
T(r,0)=T0
(4)
T2(∞,t)=T0
(5)
冻结区的半径R是随时间变化,其边界温度为冻结温度Td
T1(R,t)=T2(R,t)=Td
(6)
冻结锋面两侧始终存在如下热力关系

(7)
式中,Ψ为单位体积岩土的结冰潜热,W/m3。
为简化计算,可忽略冻结管半径r0的影响,可将冻结管作为点热源研究。式(7)可转化为
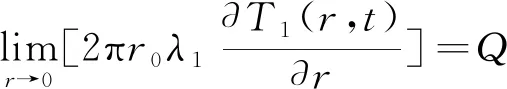
(8)
参考文献[21-22],引入新变量

(9)
将式(9)代入式(1)和式(2)可得

(10)

(11)
式中,β为两函数自变量的边界值,代表冻结锋面。
式(10)和式(11)的通解为
T1=A+BEi(u1)
(12)
T2=C+DEi(u2)
(13)
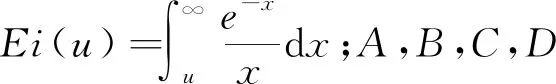
将式(6)和式(8)代入式(12)可得A,B;将式(4)和式(6)代入式(13)可得C,D。经整理,单管冻结下的土体温度分布如下
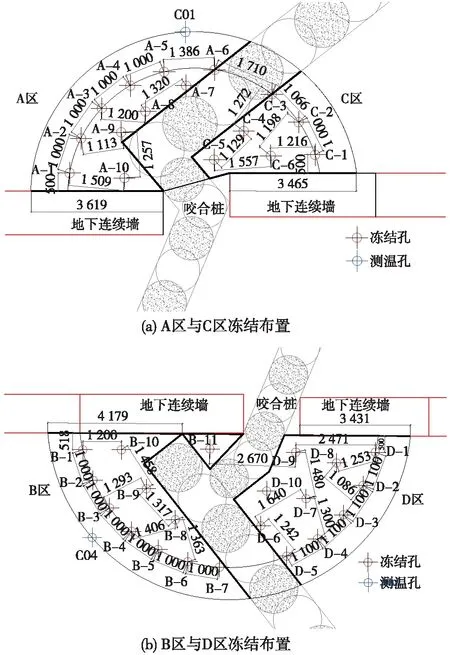
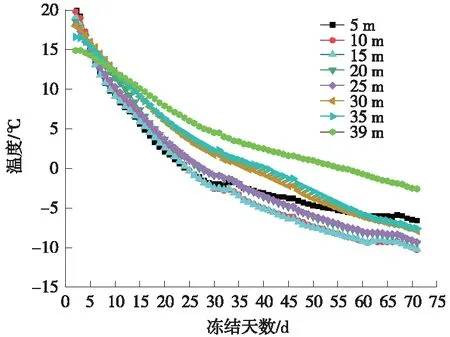
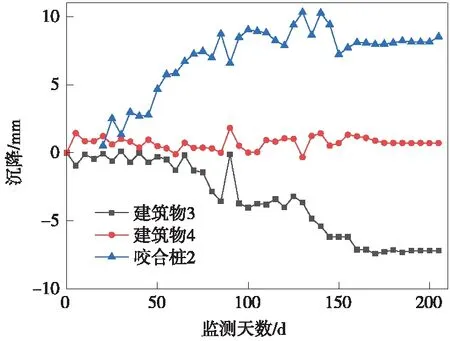
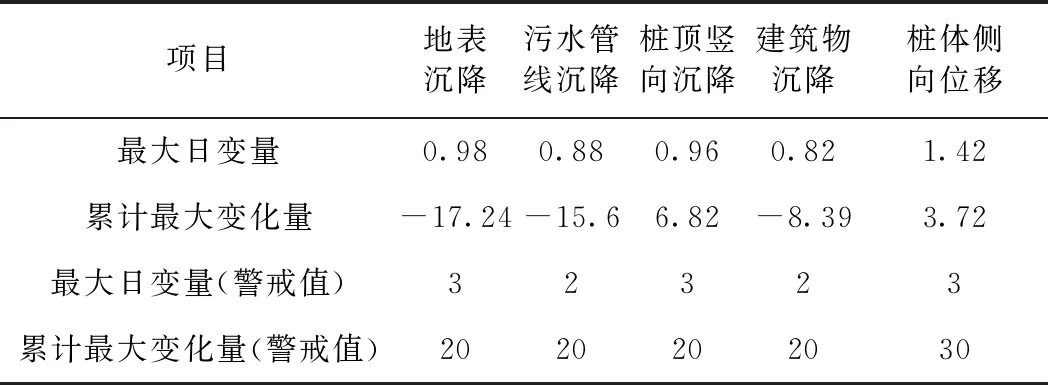
(0 (14) (15) 式中,除β外各参数均为已知值,将式(7)代入式(12)和式(13)可得关于β的超越方程 (16) 将式(9)代入式(12)和式(13)可得完整的单管冻结模型温度表达式 (r0 (17) (18) (19) 由于式(19)中的超越方程无法直接写出其解析解β,因此只能在给定参数的情况下解得瞬态温度场的数值解。 2.1.2 粉细砂岩地层单管冻结条件下温度场研究 冻结管半径r0取0.127 m,冻结管中心温度tp取-28 ℃,冻结管外表面吸收的热量Q取17 798.4 kJ/(m·d),地层初始温度T0取17.4 ℃,冻结温度Td取0 ℃,冻结粉细砂岩的导热系数λ1取221.46kJ/(m·d·℃),未冻结粉细砂岩的导热系数λ2取212.54 kJ/(m·d·℃),冻结粉细砂岩体积比热c1取2 121.4 kJ/(m·d·℃),未冻结粉细砂岩体积比热c2取2275.5kJ/(m·d·℃),单位体积粉细砂岩的结冰潜热Ψ取1.184×105kJ/m3。由此可得,冻结粉细砂岩的导温系数a1为10.44×10-2m2/d,冻结粉细砂岩的导温系数a2为9.34×10-2m2/d。 图4 单管冻结瞬态温度场的冻结锋面半径变化曲线 图5 FLAC3D计算效果 由图4可以看出。 (1)根据设计的冻结施工参数,在兰州富水粉细砂岩地层中的单管冻结40d形成的冻结壁厚度约为1.2 m,且在该时间点上理论解析计算与数值模拟结果基本一致。 (2)通过瞬态温度计算公式得出的冻结锋面与数值模拟结果在20~60d的时间范围内吻合性较好,盾构隧道相关冻结施工的积极冻结期一般也在此范围内,因此可认为在实际工程中瞬态场解析解和数值模拟计算的指导效果相当。 (3)理论上来说,随着时间的增加,冻结锋面半径会不断增大,但是增长的速率会逐渐降低,最终冻结锋面半径会稳定在一个特定值。这是由于平面点冷源引起的热流沿径向流动,热传热介质中热阻使流路径上的传热量逐渐减小,反映在宏观上即随着距冷源点距离的增加温度梯度逐渐减小。 该理论计算公式计算所得结果与已有文献[21-22]中单管冻结壁厚度对比如图6所示。 图6 单管冻结壁厚度对比曲线 可以发现,尽管存在着地层上的差异性,但总体来说,第三系粉细砂岩地层的单管冻结半径较大,冻结效果显著,即该地层对冻结法适用性较好。 第三系粉细砂岩经冻结后强度会发生改变,强度的大小与温度、含水率等因素有关。第三系粉细砂岩的基本参数如表1所示。 表1 第三系粉细砂岩的基本参数 通过现场原位测试得不同温度及含水率下冻土强度如表2所示。 表2 不同温度及含水率下第三系粉细砂岩冻结强度 MPa 本工程冻结帷幕功能仅是止水,只需强度高于水土压力防止地下水在静水压作用下渗入基坑,无特殊的抗压要求。地层水土压力偏安全考虑,按水位高程为地面高程进行计算,计算基坑加固底边缘水压力 P=0.010H=0.39 MPa 式中,H为上部土体计算厚度,m。 取最不利土层,即第三系粉细砂岩,最不利含水率4%,最高冻结温度0 ℃,以及最大地层水土压力0.39 MPa,其验算结果仍满足承压要求。且富水砂岩含水率与设计冻结温度远优于此值,所以地层最不利水土压力远低于单轴冻土的抵抗压力。 中央商务区既有围护桩深度19 m左右,省政府站地连墙施工深度39 m,为安全起见取设计冻结深度39 m。冻结壁平均温度应根据冻结的深度、承载能力,以及后期融沉对环境造成的影响综合确定。一般来说,浅层冻结工程可按照表3选取冻结平均温度[24]。 表3 冻结壁平均温度设计参考值[24] 依照表3,冻土帷幕平均温度T≤-10 ℃,取冻土帷幕平均温度为-10 ℃。 对于冻结壁厚度的确定,按照不同的计算深度需选取具体的理论进行计算(表4),由于设计最大埋深为39 m,最终根据拉麦公式进行确定。 设冻结壁为无限长弹性厚壁圆筒,冻结壁厚E的计算公式为 (20) 式中,a为冻结壁等效开挖半径,取2 m;P0为计算深度的地压,一般按P0=0.013γwH,H为计算深度,m;γw为水的容重,q为冻土设计强度,取3.417 MPa。 表4 冻结壁厚计算方法 冻结壁设计平均温度-10 ℃的冻土瞬时抗压强度为3.417 MPa,安全系数取2。按式(20)求得冻结壁厚度约为1.3 m。 本工程采用双层管冻结,故整体冻结壁厚度D按下式计算 D=D0+L (21) 式中,D为整体冻结壁厚度;D0为单管冻结壁厚度;L为两排冻结管间距,取1.2 m。所以整体冻结壁厚度为2.5 m。 冻结孔总共37个,孔间距1 000~1 200 mm,单孔深度39 m,累计冻结孔长度1 443 m。冻结孔距离围护桩边缘500 mm。布置测温孔2个,深度与冻结管相同,分别监测冻结孔冻结壁厚度,监测有无流动水存在,进而确定开挖条件,布置形式如图7所示。积极冻结期间,确保基坑周边降水不会对冷冻范围内形成扰动,最好在冻结交圈后且冻结壁达到一定厚度以后再进行微弱适量降水。 图7 冻结孔与测温孔的布置(单位:mm) 以5 m为间隔,提取测温孔监测得出的温度数据,并分别根据其随时间的变化情况绘制测点温度随时间的变化规律曲线,如图8、图9所示。 图8 测温孔A温度-时间曲线 图8和图9表明,随着冻结时间的增加,不同深度的土体的温度变化大抵相同;当冻结温度在0 ℃以上时,冻结速度较快,基本呈线性分布;当冻结温度降到0 ℃以下,土体中水分结冰,可自由流动的水含量变少,且水的导热性明显优于冰,导致冻结温度的速率随着水分不断减少而减慢,同时随着时间的增长,温度不断降低,从而形成坚实的冻结帷幕,起到堵水的效果,最终冻结帷幕温度最低可达到-12 ℃以下;当测温孔温度达到0 ℃即可认为冻结壁交圈,由图8、图9可知,A孔附近冻结壁交圈时间为55 d左右,B孔为37 d。 继续以深度为横坐标,可绘制不同时间点的地层竖向温度变化规律,如图10、图11所示。 图9 测温孔B温度-时间曲线 图10 测温孔A温度-深度曲线 如图10、图11所示,冻结帷幕的最低温度出现在冻结管埋深中段,最低温度在-10 ℃以下。当冻结深度小于10 m时,温度随着冻结深度下降,前5 m下降明显;距离地表近的地层与空气热交换作用强,热量散失快,而随着埋深的增加上覆土层与空气热交换活跃程度减少,上覆土层的保温效果越来越显著。当埋深超过10 m后,可认为土层的保温效果充分发挥,完全不与大气接触基本不造成热量散失,冻结效果稳定。随着埋深继续增加,由于冻结管中盐水的热量随着热交换而不断提高,到了35 m之后冻结效果下降明显,导致冻结温度升高。随着冻结时间的均匀增加,每5 d的温度-深度曲线间距减小,可得随着冻结时间的增加,冻结温度的降低越困难,且不同时间段各深度的土体(各条曲线)的温差基本一致。由此可知,冻结管所形成的冻结效果是均匀的,即温度场变化发展速度是均匀的,冻结效果与冻结帷幕的发展效果良好。 考虑到本工程所处的特殊地层,地面沉降变化报警值以±20 mm作为累计报警值,±3 mm作为日变量报警值。监测点布置如图12所示。 注:JZ—建筑物;SW—水位线;DB—地表监测;WS—污水管线;YH—咬合桩。图12 地表沉降监测点布置 3.2.1 地表沉降监测数据 由图13和图14可以看出,省政府侧地表与污水管线沉降变形均在10 mm以内,满足20 mm以内的要求。地表1处沉降监测点位于冻结区以外地表,距离冻结区距离适中。距离冻结区远的地表2、污水管线1两个沉降监测点的沉降变化不大,受冻结施工与基坑开挖的影响小。从监测第48 d开始进行冻结作业,随着冻结作业的进行在监测的第50 d后,污水管线1处发生了幅度较大且速度快的沉降变形。这是因为在冻结区进行冻结时,冻结壁开始发展,土壤中的水分逐渐转化为冰体而减少,此时周围土体中的水分将不断向冻结区域中的冻结壁上迁移来补充水位,导致污水管线1处沉降监测点处土体水位下降进而产生沉降变形。当监测天数达到120 d时积极冻结已经完成,开始进入维护冻结阶段,冻结壁已经不再发展,所以地下水位也同时进入稳定状态,污水管线1处沉降监测点的沉降变形也趋于稳定。地表沉降3、4处沉降监测点距离冻结区距离近,污水管线2处沉降检测点位于冻结区域内。在基坑冻结施工前,基坑与冻结区进行的降水导致这3个监测点随着地下水位下降发生了沉降变形。当监测到第48 d及积极冻结作业开始时,地层中水分逐渐被冻结成冰,地层土体发生冻胀,这3处土体监测点发生了隆起变形。监测到第120 d后,积极冻结完成进入维护冻结与基坑开挖阶段,省政府侧3处监测点受基坑开挖的影响,根据距离基坑的远近不同产生了相应的沉降。 图13 中央商务区侧地表沉降曲线 图14 省政府侧地表沉降曲线 3.2.2 建筑物以及咬合桩沉降监测数据 图15和图16分别为两侧建筑物与咬合桩的沉降监测结果。可以看出,各建筑物与咬合桩沉降监测点的变形量均小于10 mm。距离冻结区远的建筑物1、4沉降监测点,受到冻结作业与基坑开挖施工的影响十分小,所以其沉降基本不变。而建筑物2、3沉降监测点,距离冻结区距离适中,在监测第48 d后即积极冻结施工开始时,冻结区冻结壁发展,冻结区域内土体中水分结冰导致冻结区水位下降,未冻结区土体(即建筑物2、3沉降监测点)中水分开始不断地向冻结壁上迁移并补充地下水位,造成其逐渐产生较大沉降,随着监测进行到120 d,积极冻结结束伴随着维护冻结与基坑开挖施工的开始,此时两处建筑物将受其影响继续产生沉降直到结束。咬合桩1、2号沉降监测点处有较明显的抬升,这是因为冻结时此处位于冻结区域以内,积极冻结阶段地层土体的冻胀使得桩基有一定的上抬,在基坑的开挖进行中,随着基坑中土体的减少而下沉直至稳定。 图15 中央商务区侧建筑物地表沉降曲线 图16 省政府侧建筑物地表沉降曲线 3.2.3 监测数据总结 监测数据表明:地表沉降,污水管线沉降,桩顶竖向沉降,建筑物沉降和桩体侧向位移的最大日变量和累计最大变化量都符合变化量要求,隆起沉降得到了控制。沉降监测数据整理如表5、表6所示。 表5 省政府站监测数据 mm 表6 中心商务区监测数据 mm 通过对第三系粉细砂岩深大基坑咬合桩局部冻结加固设计与监测结果分析,主要得出以下结论。 (1)提出了单管冻结温度场计算公式,并对第三系粉细砂岩地层进行了适用性分析,结果证明,单管冻结壁较大,冻结法适用性较好。 (2)根据第三系粉细砂岩的工程特性,采用整体冻结+局部差异冻结,确定了适用于该特殊软弱地层的冻结方案,并分析了冻结参数取值。 (3)长期监测数据表明,冻结区域温度的降低速率与地层水分含量相关,并随时间呈现逐步减慢的趋势,55 d左右冻结帷幕基本形成,此时基本达到开挖条件,冻结帷幕形成和发展过程较为稳定。 (4)根据现场监测结果,省政府侧地表沉降变形最大为6 mm,污水管线沉降最大为10 mm,满足20 mm以内的要求,且冻胀引起的地表隆起现象不明显;局部冻结施工有效降低了周边地下水位,且开挖过程中地层水位稳定,未再出现严重涌水、涌砂事故。


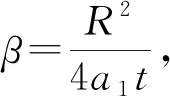



2.2 冻土承压计算


2.3 冻结设计参数的确定

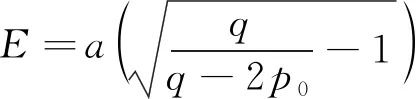

2.4 冻结孔及测温孔布置
3 施工监测
3.1 温度监测


3.2 沉降监测





4 结论
