基于压缩压胀分区的高铁地基水平位移分析方法

郭帅杰,宋绪国,陈洪运

(1.中国铁路设计集团有限公司,天津 300308； 2.城市轨道交通数字化建设与测评技术国家工程实验室,天津 300308)

1 研究背景

我国高铁工程建设中，高铁路基通常采用填土路堤结构形式[1]，高铁路堤堆载在引起地基沉降变形的同时，不可避免地引起地基深层水平位移[2-3]。但现阶段，无论是铁路工程建设施工还是专门的学术性研讨，高铁地基变形分析主要围绕路堤堆载引起的地基沉降变形展开[4-5]，关于地基深层水平位移分布规律及分析计算方法方面并没有引起充分的重视。实际上，高铁路堤堆载引起的地基深层水平位移，无论是变形幅值还是影响范围都是不可忽略的[6-7]。特别是对于新建铁路临近存在既有高铁线路、地下管线或其他构筑物，地基深层水平位移将直接威胁这些临近工程的安全性[8-11]。

当前，关于地基水平位移的分布规律和分析方法方面的研究主要出现于我国沿海和长江中下游地区的软土地基，真空预压、超载预压将引起既有公路路基的明显变形[12-14]，相关研究主要围绕地基水平位移同沉降位移的比值关系、水平位移分布规律、测试方法等方面展开。关于地基水平位移分析，目前主要采用数值仿真分析方法，通过有限元或有限差分数值仿真分析软件，建立数值仿真分析模型，进行路堤堆载引起的地基水平位移计算[15-18]。理论分析方面主要基于Boussinesq和Mindlin理论中的单点荷载位移解[19]，但由于两种理论方法积分解答的复杂性且仅适用于分析均质地基，实际工程中推广应用存在较大困难。当前，各类规范关于路堤堆载引起的地基沉降分析，仍以竖向附加应力计算为基础的分层总和法为主[4]。

针对上述高铁路堤堆载对地基深层水平位移的严重影响以及相关理论分析方法的局限性，研究提出一种基于Boussinesq水平应力分布和地基压缩压胀分区的水平位移分层总和法应用于高铁地基深层水平位移分析计算，并对该方法的基本理念、参数定义、分析思路、数值仿真验证等进行具体的分析讨论，确定高铁地基深层水平位移分析方法的一般性流程。

2 地基深层水平位移理论分析方法

对于半无限空间均质地基，Boussinesq理论可精确得到地表集中荷载引起的地基内部任意一点的应力、应变，通过应变积分进一步得到对应位置的竖向、水平位移。根据Boussinesq理论求解条件，竖向集中力作用下的地基内部附加应力状态如图1所示。

图1 集中荷载作用下的地基附加应力计算示意

图1中，地表集中荷载P引起的地基内部M点位置处水平位移解和水平应力解的表达式分别为式(1)和式(2)。

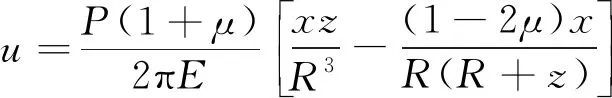
(1)

(2)

式中，P为集中荷载；u为集中荷载引起的地基内任一点位置处的水平位移；E为地基弹性模量；μ为地基土体泊松比；x，y，z为计算点M相对于集中荷载作用点的位置坐标；r为计算点M与集中荷载作用点间的水平距离，r=(x2+y2)0.5；R为计算点M位置与集中荷载作用点的空间距离，R=(x2+y2+z2)0.5。

Boussinesq理论关于地基土层的附加应力解答以及基于此的分层总和法，在土力学地基沉降计算中得到广泛应用，并已被广泛纳入各类规范，如《建筑地基基础设计规范》、《建筑地基处理技术规范》以及《铁路路基设计规范》等。但是，现有分层总和法主要针对地基沉降分析展开，关于地面堆载引起的地基深层水平位移往往仅强调现场监测，并未开展过多的理论分析研究。此外，式(1)中Boussinesq理论关于地基深层水平位移解析主要针对均质地基的单点集中荷载，对于大面积非均匀地面堆载，式(1)解析式仍然存在较大的应用局限性。

3 高铁地基水平应力及位移分布特征

3.1 数值仿真分析方法

数值仿真软件能够准确模拟高铁路堤堆载引起的地基各种变形行为，通过建立的高铁地基物理模型和土体本构模型，实现地基沉降位移、水平位移以及各方向附加应力的求解分析。具体研究中，以典型高铁路基断面为分析对象，路堤顶宽14 m、底宽28 m、填高4.5 m，地基尺寸为100 m(深度)×200 m(宽度)，应用摩尔-库伦本构模型。数值仿真分析中，应用FLAC3D软件建模，通过路堤堆载引起水平应力和水平位移提取，得到路堤堆载引起的右半侧地基内部水平位移和水平应力分布如图2所示。

图2 基于数值仿真的地基水平位移及应力分布

根据图2进一步提取不同深度位置处路堤堆载引起的横断面方向上的地基水平位移和水平应力，得到对应深度位置处的地基土体水平位移和水平应力，如图3。

图3(a)中，地基表面z=0 m位置处水平位移为指向中心位置方向的负向位移，而地基深部均为指向侧向边界方向的正向位移。深度方向上，地基水平位移在约20 m深度处达到最大值，并且水平位移达到最大值的深度同路堤堆载大小及范围直接相关，之后水平应力沿深度方向逐渐减小；水平方向上，地基水平位移沿侧向边界方向先增大后减小，并在边界位置减至为0。对于图3(b)中的水平应力横断面分布，其表现为同地基水平位移近似的分布规律，路堤堆载引起的水平应力在深度方向上递减，横断面方向表现为先增大后减小趋势。此外，对比图3中地基内部水平位移和水平应力极值点，两指标的水平分布极值点位置基本相同，那么通过相同深度横断面的最大附加应力位置坐标，即可确定路堤堆载引起的最大水平应力位置。

图3 基于数值仿真的地基水平位移和应力横断面分布

3.2 Boussinesq理论方法

根据式(2)，对数值仿真分析方法关于高铁地基计算工况进行理论分析，得到图4(a)路堤堆载引起的右半侧地基水平应力分布等值线，在此基础上，进一步提取不同深度横断面位置处水平应力，得到图4(b)中Boussinesq理论确定的水平应力分布。

图4 基于理论分析的地基附加应力及横断面分布

对比图2(b)和图4(a)中数值仿真和Boussinesq理论关于路堤堆载引起的水平应力分析结果，两种方法关于地基一定深度范围内的水平应力分析结果相近，但在地表和边界附近存在较大差异。其中，理论方法不存在侧向和底面边界影响，而数值仿真方法由于边界限制，水平应力存在局部突变，但对于远离边界区域的地基附加应力同理论分析结果仍具有很高的相似性。图4(b)为不同深度位置处的路堤堆载引起的水平应力断面分布，Boussinesq理论得到的地基水平应力均为正值，随横向间距存在明显的先增大后减小趋势，同数值仿真分析结果较为接近，说明应用Boussinesq理论确定地基内部水平应力分布是合理的。

4 地基压缩压胀分区与水平位移分析

4.1 地基水平变形压缩压胀分区方法

对于中心对称高铁地基，理论方法关于地基对称面一侧的附加应力方向完全相同，其对单元土体的作用应表现为一致性的规律。但中央对称地基对称面位置以及边界位置处水平位移均为0，那么水平应力引起的地基水平位移必将存在极值点。极值点外侧指向侧边界的区域为地基土体压缩区，极值点内侧指向路基中心对称面的区域为地基土体压胀区，两区域的分界线为不同深度横断面方向的最大附加应力位置点连线。根据图4中Boussinesq理论确定的地基附加应力分布，得到图5对称梯形路堤堆载作用下的地基变形压缩压胀分区。

图5地基土体水平变形压胀区和压缩区分界线确定过程中，主要基于图4(b)中横断面附加应力极值点位置，当不存在最大附加应力极值点时，取靠近边界位置的第一个附加应力突变点位置。地基深度大于5 m后，地基压胀区和压缩区的分界线基本为一条倾角45°直线，小于5 m时为坡脚附近的折线。

图5 地基水平位移计算简化分区示意

4.2 地基水平位移的分层总和法计算

基于Boussinesq理论确定的地基水平应力计算水平位移过程中，以侧向边界为水平位移零点，根据不同深度地层水平压缩模量[20]，通过分层总和法对图5中的地基压缩区土体单元的水平压缩应变进行累加，并在压胀压缩区分界线位置达到最大，之后向路基对称面方向衰减至0。需要特别说明的是，图5中地基压胀区位移采用附加应力比分配方式，压胀区水平位移同路堤堆载引起的水平应力水平正相关，通过地基压胀区单元土体水平变形量的累加，得到累计的地基水平位移分布。

按照上述思路，对Boussinesq理论确定的地基水平应力进行相同处理，分别得到图6(a)路堤堆载作用下地基水平位移等值线分布和图6(b)不同深度位置处的水平位移横断面分布。

对比图2(a)、图3(a)以及图6，理论分析结果同数值仿真结果无论是在变形数值还是再分布形态上均较为接近，但图6中压缩压胀分界线位置处水平位移存在突变。相较于数值仿真结果，理论方法确定的地基水平位移分布不够平顺圆滑，最大水平应力线附近的地基水平位移仍需要进一步的处理简化。

图6 基于水平位移压缩压胀分区的水平位移分析结果

通过算例关于4.5 m填高典型高铁路堤堆载引起的地基水平位移分布的对比分析，研究提出的基于地基压缩压胀分区的水平位移计算思路，属于一种基于成熟Boussinesq理论的水平位移简化分析方法，并在一定程度上接近于数值仿真分析结果，这也为高铁地基水平位移分区特征的分析评估提供了一种全新的思路和方法，为高铁地基水平位移计算的进一步优化奠定了基础。应用Boussinesq理论确定地基水平位移，主要基于地基土体压缩区和压胀区假定，并将路堤堆载引起的水平应力极值点作为两区域的分界线，但是该假定的合理性、地基压胀压缩分界线的确定方法等方面仍需要进一步分析讨论。

5 结论

路堤堆载引起的地基深层水平位移的分析评价是高铁建设中面临的新问题，特别是存在既有构筑物情形下，当前主要基于数值仿真技术分析计算。由于缺少必要的理论方法验证，数值仿真结果的有效性需要进一步的验证。基于地面荷载引起的地基附加应力分布特点，参照地基沉降分析中的有限元分层总和法，新提出一种基于地基水平变形压缩压胀分区的水平位移分析方法，一定程度上解决了高铁地基深层水平位移分析计算问题。研究结论如下。

(1)路堤堆载引起的地基最大水平位移出现于坡脚外一定深度位置处，该深度同路堤堆载大小和范围相关，最大水平位移和水平应力均较小，且向边界方向快速衰减。

(2)地基深层水平位移水平分布存在极值点，极值点连线大致为45°倾角直线，并可作为地基深层水平位移压缩压胀分区的界限，压缩区采用分层总和法计算水平位移，压胀区基于路堤堆载引起的水平应力大小的相对比值分配确定。

(3)基于压缩压胀分区的高铁地基深层水平位移分析结果同数值仿真结果较为接近，但在压缩压胀分界面位置存在突变，需要对压缩压胀分区方法进一步优化。

(4)研究提出的高铁地基深层水平位移理论分析方法是对Boussinesq理论的简化应用，对分析路堤堆载作用下的地基水平变形问题具有重要的参考价值。