基于线性拟合模型的苹果大小分级方法

郑纪业，张琛，刘光，王风云

（1.山东省农业科学院科技信息研究所，山东济南 250100；2.中国移动通信集团山东有限公司青岛分公司，山东青岛 266000；3.济南市中小企业公共服务中心，山东济南 250099）

我国苹果种植面积大、产量高［1］，与之对应的是产销过程中占用大量的人力资源，与日俱增的人力成本压缩了苹果产销的利润空间。为减少人力成本，加速农业现代化，科研人员从不同角度做了相关研究，其中苹果分级因需求大、可行性高而成为研究热点。

当前我国苹果分级主要依赖人工进行，也有少量依靠机械方式进行［2］。随着机器视觉的发展，依据图像进行分级成为主要研究方向［3，4］。大小分级是苹果等农产品分级的重要组成部分，受到国内外诸多关注［5-8］。Hayrettin等［9］利用苹果二值图像在x、y方向上的像素数计算苹果直径；Paulus等［10］用表面积、直径和体积三特征表征苹果大小。国内当前有关农产品大小分级的研究则主要用到最小外接矩形法［11，12］、拟合圆法［13，14］、最大横切面直径法［15］等，这些方法可以较准确地求出图像中苹果直径像素数，但易受果形影响，存在不同程度偏差。而且在求出苹果直径像素数后，还需要对直径像素数与实际直径建立映射关系，因为苹果大小变化会影响图像中像素数与实际尺寸的比例，所以基于固定比例的直径计算方法会随着苹果直径变化程度的增大而产生更大的误差。若要减小直径计算误差，就需要改进直径像素数与实际直径的映射关系。刘新庭等［14］利用与苹果大小相近的球体建立图像直径与实际直径的映射关系，但苹果实际形状与球体模型一致程度有限；陈艳军等［15］利用苹果三幅不同果面图像的直径像素数与苹果实际直径建立线性模型进行映射，三幅图像能一定程度上反映苹果大小，但是却没有计算出图像中苹果的实际直径。可见，利用上述方法虽能对苹果大小分级，根据各自分级标准也均能得到较高准确率，但仍存在较大的平均误差。

当前苹果大小分级难点在于将苹果直径像素数准确映射到实际直径［16］，针对该难点，本研究设计一种关于直径像素数与实际直径的线性模型，并用最小二乘法对线性模型进行拟合。该模型采用不同大小的苹果数据进行建模，与球体模型［14］相比更符合苹果实际形状特点，与多幅图像建立的线性模型［15］相比能更准确计算图像中的苹果直径。同时为进一步提升分级准确率，本研究还对直径像素数计算方法做了改进，利用HSV颜色空间分割苹果区域并提取苹果轮廓，用苹果轮廓最外侧点迭代求最小外接圆，以最小外接圆直径作为苹果直径。经过上述改进，本分级方法的准确率不仅能满足应用需求，而且明显降低了分级过程中的计算误差。

1 材料与方法

1.1 试验材料与设备

试验材料为烟台栖霞生产的“烟富3”苹果，共75个，大小在70～95 mm之间。测量苹果实际大小后，按总体大小分布规律从中选择40个作为建模集，剩余35个作为测试集。

试验装置如图1所示，其中相机型号为维视MV-VEM200SC，相机到传送带平面的高度为61 cm，光圈型号为维视 AFT-RL 12068，计算机CPU为Intel Core i3。相机位于传送带正上方，传送带将苹果从上料口传送至相机下，光圈用于照明苹果，相机采集的数据传送至计算机进行大小分级。

试验使用语言开发工具Microsoft Visual Studio 2013以及计算机视觉函数库OpenCV对图像进行处理。

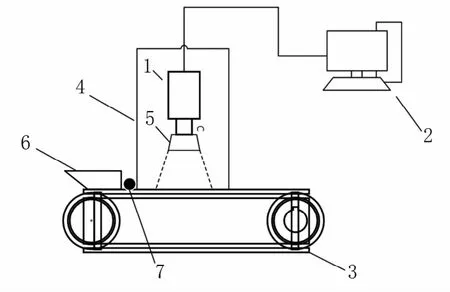
图1 试验装置示意图

1.2 试验方法

苹果实际直径依据垂直于果梗-花萼连线的最大横切面测得：试验中用游标卡尺对苹果最大直径测量3次，若有与另两次数据差距较大的异常值，则重新测量，最终取3次测量的平均值作为苹果实际直径。

苹果图像由图1试验装置采集：将苹果从上料口放置于传送带上，匀速传送至相机下，由传送带上的触发装置感应到苹果后进行拍照，图像传送到计算机进行处理，并给出分级结果。图像处理流程如图2所示。

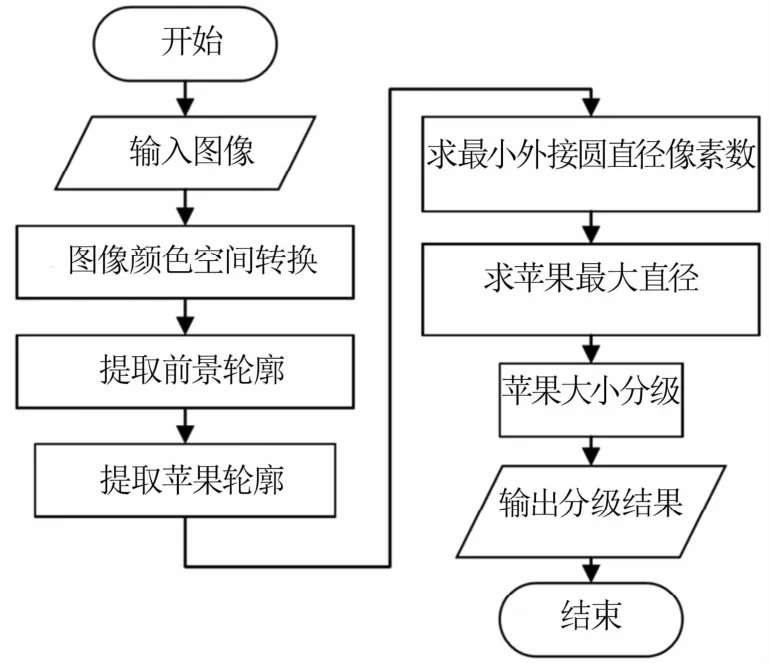
图2 图像处理流程

2 结果与分析

2.1 苹果轮廓提取

提取苹果轮廓需要先从图像中分割出苹果区域［17］，可利用阈值分割实现。阈值分割［18］具有快速、直观的特点，它用一个或多个阈值分割图像中的不同内容，按阈值设置方式不同可分为自适应阈值分割和固定阈值分割。大津法［19］是自适应阈值分割方法中的代表方法，对图3a所示苹果图像进行分割得到如图3b所示苹果区域，可见，受苹果果形影响，光反射率由中心向四周呈降低趋势，图像中苹果区域灰度存在梯度变化，分割结果损失部分边缘，难以将苹果区域提取完整。而用固定灰度阈值对图3a进行分割可以较完整提取到如图3c所示的苹果区域，可见，固定阈值分割虽然不具备多变环境的适应性，但是在图像采集环境固定的情况下分割效果优于自适应阈值分割。但由于苹果区域存在灰度变化，灰度取值范围较宽，利用固定阈值分割出苹果区域的同时也会提取到噪声区域。为更准确地提取苹果区域，本研究先利用多色彩颜色空间进行前景提取。

2.1.1 图像颜色空间转换 通常相机采集到的图像在计算机视觉上是用RGB颜色空间表达的。不同于RGB颜色空间，HSV颜色空间［20］是用色调（H）、饱和度（S）、明度（V）表达色彩，在表达图像色调、鲜艳程度以及色彩明暗上更具有优势，且便于进行颜色之间的对比，所以本研究首先将相机采集到的苹果图像由RGB颜色空间转换到HSV颜色空间以进行图像分割。颜色空间转换通过对图像像素红（R）、绿（G）、蓝（B）三数值的操作实现，转换公式如下：

2.1.2 HSV阈值分割 同种苹果不同个体的H、S、V值分布区间具有共性，用采集图像中的苹果区域样本与非苹果区域样本进行试验，确定出苹果H、S、V的取值范围，在HSV颜色空间提取苹果区域图像。图4a为两种环境下采集到的苹果图像，图4b为用固定灰度阈值分割两种环境下苹果区域的效果，图4c为用HSV阈值分割两种环境下苹果区域的效果。可见，利用HSV阈值分割能将苹果较完整地从背景中分割出来，且能在一定程度上与杂物、反光等噪声区分，比灰度阈值分割有更好的环境适应性。

2.1.3 苹果轮廓提取 由于传送带上可能存在杂物或其他影响分割准确性的因素，且果梗、花萼及缺陷区域也会对分割造成干扰，提取的前景二值图像中会存在噪声，需要去除噪声以准确提取苹果区域。鉴于后文中求最小外接圆需要用到苹果轮廓，且噪声轮廓与苹果轮廓在大小上存在明显差异，本研究通过判断轮廓大小去除噪声。首先提取前景图像轮廓，然后遍历所有轮廓，将大小低于阈值的轮廓删除，则轮廓信息中只保留如图5所示苹果轮廓。

2.2 确定最小外接圆并计算苹果直径像素数

图像中的苹果直径根据苹果轮廓求得，以像素数的形式体现。当前常见求轮廓直径的方法中，最小外接矩形法［12］通过旋转轮廓确定最小外接矩形，但因苹果果形不规则易产生误差；同心外接圆法［14］以苹果图像质心作为外接圆圆心求苹果最小外接圆，但是苹果图像质心不完全与苹果实际最小外接圆圆心一致，因此该方法求出的同心外接圆通常大于真正的最小外接圆。本研究采用轮廓外侧点迭代求圆的方法，求出苹果区域最小外接圆，得到更准确的直径像素数。

该方法首先遍历轮廓所有点，确定上、下、左、右最外侧四点A、B、C、D，查找四点所能确定的最大三角形，求该三角形最小外接圆，假设三角形三顶点分别为 A（x1，y1）、B（x2，y2）、C（x3，y3），则圆心O坐标（x，y）由（4）（5）式求得，半径R由（6）式求得：

图5 苹果轮廓提取结果

再次遍历轮廓所有点，检查是否有点在前一步所求圆之外，即轮廓到圆心的距离大于半径R。若无点在圆外，则该圆为苹果轮廓最小外接圆，直径为苹果轮廓直径；若有点在圆外，则将圆外距离圆心最远点E与先前四点A、B、C、D组成四个不同组合 ABCE、ABDE、ACDE、BCDE。以组合ABCE确定包围4点的最小圆，判断组合外的D点是否在该圆内，若不在圆内，则求解其他组合确定的最小圆，并判断组合外的一点是否在该组合所确定圆内。如此重复进行，直到某组合外的一点在该组合所确定的最小外接圆内，则该圆为苹果轮廓新的最小外接圆。

用新的最小外接圆验证是否有轮廓在圆外，若有点在圆外，重复上述过程，直到轮廓所有点都在外接圆内，则该外接圆为苹果区域最小外接圆（图6），其直径像素数代表苹果最大横切面直径。

2.3 构建线性模型计算苹果直径

图像中的苹果直径以像素数体现，不能直接用于分级，还需将其映射为以毫米为单位的数值才能用于苹果分级。本研究首先尝试将标定尺放在传送带上拍照，获得图像像素数与实际尺寸的比例，进而求出图像中苹果的直径，结果发现利用该方法计算得到的苹果直径明显偏大（表1）。经分析，原因主要在两方面：一是苹果形状类似球体，其最大直径所在横切面高度明显高于传送带，而相机取景范围近似为锥体，相同大小横切面的高度越高，测量得到的直径越大；二是苹果外形不规则，果梗-花萼的连线与传送带平面并不一定垂直，而是可能略微倾斜，改变了苹果横切面在图像上投影的面积。由此可见，用标定尺比例作为图像与实际大小的映射关系不能满足分级要求。

图6 苹果区域最小外接圆

表1 按标定尺比例计算的苹果直径及误差

针对上述问题，本研究采用最小二乘法对苹果直径像素数与实际直径的关系进行拟合，以计算苹果直径。首先以苹果直径像素数为横坐标，苹果实际直径为纵坐标，生成图7所示散点图，发现直径像素数与实际直径存在线性关系，故设计线性模型y＝ax＋b，其中y为苹果直径（mm），x为直径像素数。

图7 苹果直径像素数与实际直径对应关系

最小二乘法［21］是一种数学优化技术，通过最小化误差平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便求得未知数据，并使所求数据与实际数据之间误差平方和最小。基于该性质，本研究利用最小二乘法求解线性模型。由线性模型y＝ax＋b可得最小二乘式如下：

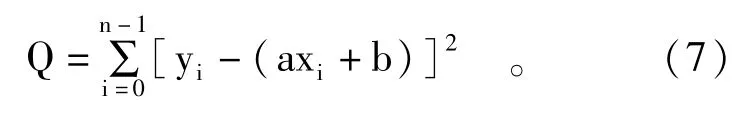
为计算参数a、b，需对最小二乘式求偏导：

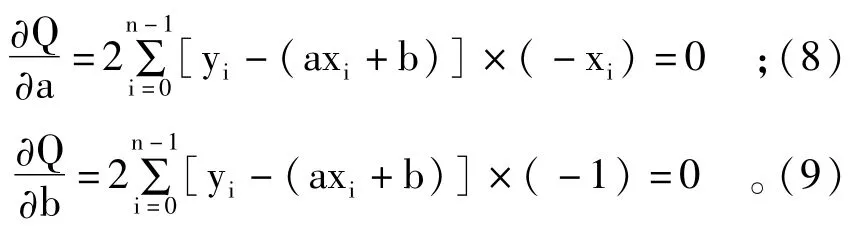
最终计算得到a、b如下：

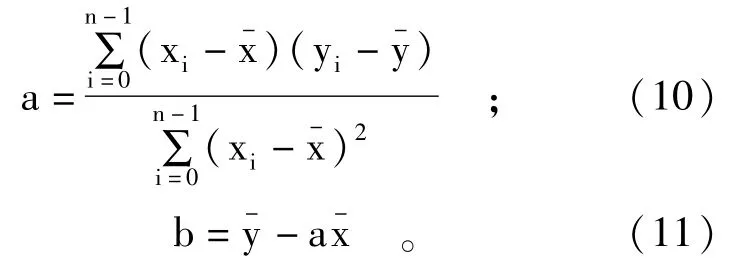
计算建模集中苹果直径像素数，用最小二乘法对建模集的像素数据及实际直径数据进行拟合，得到线性模型y＝0.0724554x＋1.80354。用测试集对该模型进行测试，计算所得苹果直径与实际直径的对比，如图8所示。可见，利用本研究模型计算得到的苹果直径与实际直径高度一致，利用该模型能比较准确地预测出苹果实际直径。

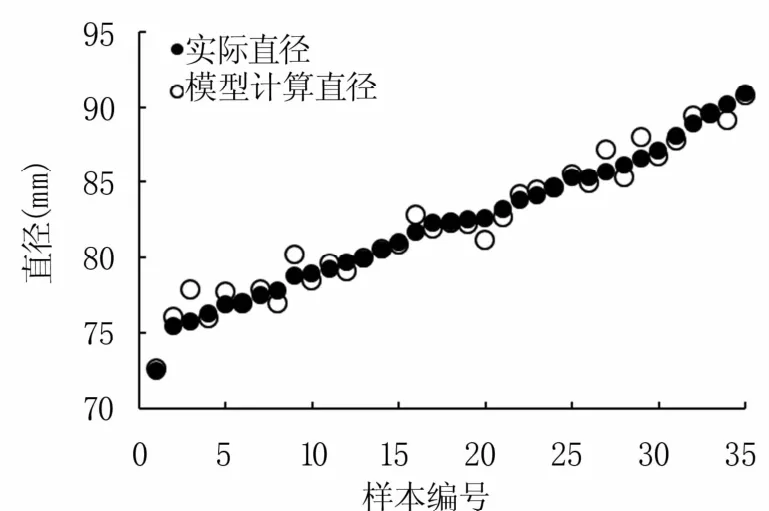
图8 测试集苹果直径计算值与实际值对比结果

2.4 基于线性拟合模型的苹果大小分级结果

通常苹果大小分级依据鲜苹果标准GB／T 10651—2008及烟台苹果标准GB／T 18965—2008进行，分级标准见表2，其中直径为苹果最大横切面直径。

表2 苹果大小分级标准 （mm）

本试验所选的75个苹果样品为随机选取，符合“烟富3”品种的大小分布规律，实测直径均大于70 mm，大于75 mm的有72个，所以仅依据上述标准对本研究构建分级方法进行验证，参照价值有限。为更好体现分级方法准确率，将苹果按实测直径分为数量大致相等的三类进行分级，同时为客观体现方法的准确性，选用平均测量误差作为方法准确性的另一评判标准。

通过分类，所选75个样品中，直径在70～80 mm之间的有25个，80～85 mm之间的有27个，85～95 mm之间的有23个，故设计“烟富3”分级标准如表3。

表3 “烟富3”大小分级标准 （mm）

基于表3所示分级标准对本研究方法的分级准确率进行验证。结果（表4）显示，测试集利用本研究方法的分级准确率为91.4%，总体分级准确率为92.0%，平均误差均为0.56 mm，测试集与样本整体的准确率及平均误差相近或一致，表明试验结果较为稳定，该方法具有较高的可靠性。

表4 本研究方法分级准确率及平均误差

3 讨论与结论

本研究通过改进苹果直径像素数计算方式以及利用最小二乘法构建直径像素数与实际直径的映射模型，提高了苹果大小分级的准确性。在改进直径像素数计算方式时，利用HSV颜色空间分割苹果区域，并用基于轮廓外侧点的最小外接圆法计算苹果最大横切面的直径，相比现有方法提高了苹果直径检测的准确性。针对苹果直径像素数与实际直径难以准确映射的问题，本研究对直径像素数与实际直径进行拟合，用最小二乘法构建两者的线性拟合模型，提高了直径像素数与实际直径映射的准确度，减小了苹果最大横切面高度及果形变化等客观因素对分级结果的影响。

利用本研究方法对75个苹果进行大小分级试验，总体分级准确率为92.0%，苹果直径平均计算误差为0.56 mm。刘新庭等［14］基于最小外接圆直径对30个65～95 mm的苹果按75-70-65 mm标准进行分级，分级准确率96.67%，平均测量误差为0.94 mm。陈艳军等［15］基于机器视觉的最大横切面直径对40个55～95 mm的苹果按85-75-70 mm标准进行分级，分级准确率87.1%，平均测量误差0.67 mm。余扬［22］基于多特征对60个60～100 mm的苹果进行分级，苹果直径的平均测量误差为4%；利用本研究样本对其方法进行验证，平均测量误差为3.30 mm。考虑到各文献样本及分级标准不同，分级准确率不能完全代表分级效果，故采用平均测量误差来更客观地反映方法分级效率，可见，本研究建立的苹果大小分级方法分级准确率较高，平均测量误差小，能够满足苹果销售的市场需求。

但利用本研究方法进行苹果大小分级时仍存在一定误差，分析误差产生的原因，主要在两方面：一是苹果最大横切面高度虽然与苹果大小有相关性，但变化不完全一致，对模型准确性造成一定影响；二是苹果倾斜角度的不规则变化使图像中苹果横切面投影大小有不同程度的改变。基于此，后续研究将从减小或解决苹果姿态对最大横切面投影影响的角度出发对分级方法进行改进，以进一步提高苹果大小分级的准确性。另外，随着农业现代化的推进及市场需求的变化，农产品分级目的会发生相应改变，对分级准确性提出更高的要求，建立适合各种分级目的且具有更高分级准确性的方法将是今后农产品分级研究的重要研究方向。