非线性自回归模型误差密度估计的Berry-Esseen界

刘天泽, 张 勇, 谭希丽

(1. 北华大学 数学与统计学院, 吉林 吉林 132013; 2. 吉林大学 数学研究所, 长春 130012)

1 引言及主要结果

考虑如下非线性自回归模型

Xi=rθ(Xi-1,…,Xi-s)+εi,

(1)

其中: {Xi}是一个严平稳过程;rθ为s→上的实值可测函数,θ=(θ1,…,θq)′∈Θ⊂q是参数向量; {εi}是均值为0、 方差为σ2的独立同分布随机误差, 有未知的密度函数f. 假设Xi-1,…,Xi-s和{εi}独立. 显然, 模型(1) 包含了一系列非线性时间序列模型, 在金融统计中已得到广泛关注[1]. Cheng等[2]研究了随机误差的拟合优度检验; 文献[3-5]讨论了随机误差的密度函数估计问题； 傅可昂等[6]研究了重尾非线性模型自加权M-估计的渐近正态性.

Berry-Esseen不等式[7-8]表示随机变量序列{Xn,n≥1}前n项正则化和的分布函数Fn(x)与标准正态分布函数Φ(x)之差趋于零的收敛速度, 目前已取得许多研究成果. Parzen[9]证明了独立同分布情形下, 随机变量序列核密度估计的Berry-Esseen 界可达O((nhn)-1/2)； 文献[10-11]研究了不同情形下的Berry-Esseen界问题. 本文基于文献[9], 给出非线性自回归模型误差密度估计的Berry-Esseen界.

下面给出模型(1)的误差核密度函数. 假设核函数K(·)是上给定的Borel可测函数, 窗宽hn>0是与n有关的常数, 满足模型(1)的误差密度估计为

(2)

下面给出几个基本假设.

(3)

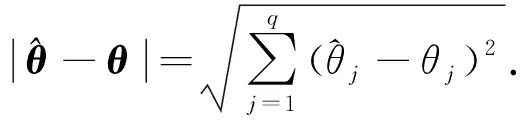
(H3) 假设K是上的有界变差函数,K″是有界的, 且对每个δ>0, 有

注1由模型(1), 假设Xi-1,…,Xi-s和{εi}独立, 易知εi与Yij独立.

注2Klimko等[12]给出了随机过程的条件最小二乘估计满足式(3)的重对数律； 非线性情形下, Liebscher[13]研究了非线性自回归模型参数θ的M估计的重对数律.

本文假设C表示正常数, 在不同之处可表示不同值,Φ(·)表示标准正态分布函数. 本文主要结果如下：

定理1对定点t∈, 密度函数f(t)满足一阶Lipshitz条件, 即

|f(t)-f(t-y)|≤C|y|, ∀y∈.

(4)

假设窗宽hn满足

则对任意的y∈, 在假设条件(H1)～(H3)下, 有

(5)

2 引 理

引理1[14]设X,Y为两个随机变量, 对任意a>0, 有

引理2假设1≤i≤n, 1≤j,l≤q, 则

证明: 由假设条件(H1)易得结论.

引理4假设定理1的条件成立, 则有

证明: 注意到

且

因为Yij和εi独立, 所以由式(4)和条件(H3)可得

由引理2, 有

再考虑I12, 由式(4)和条件(H3), 有

由Cr不等式和引理2可知,

另一方面, 由条件(H2)可得

从而有

再注意到

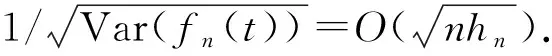
引理5假设定理1 的条件成立, 则有

证明: 注意到

且

先考虑I21, 由引理2有

再考虑I22, 由Cr不等式和引理2可知,

另一方面, 由条件(H2)可得

因此可得

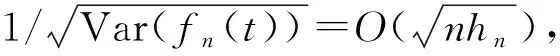
引理6假设定理1的条件成立, 则有

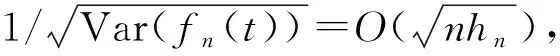
引理7假设定理1的条件成立, 则有

从而可得

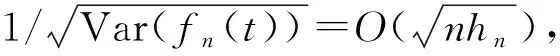
3 定理1的证明

下面证明定理1. 由式(1),(2)和Taylor展开, 有

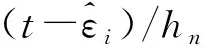
由Markov不等式可得