感悟多样策略 渗透数学思想

摘 要：在小学数学教学中，教师要积极渗透优化、集合、数形结合、类比等数学思想，使学生逐渐掌握解决问题的不同方法，感悟问题解决策略的多样化，从而点燃学生思维的火花，发展学生的数学思维。文章分析了小学数学教学中渗透数学思想的策略，以期为相关教师提供参考。

关键词：问题解决;数学思想;教学策略

中图分类号：G427                                 文献标识码：A                                     文章编号：2095-9192（2021）34-0022-02

引  言

《义务教育数学课程标准（2011年版）》（以下简称《课程标准》）重视数学问题解决策略的多样化，注重拓展学生解决问题的思路。教师要在学生解决问题的过程中潜移默化地渗透数学思想，提升学生的数学思维能力，这对学生的终身发展有十分重要的意义。

一、在问题解决中体会优化思想，提升学生数学建模能力

人教版小学数学教材编排了一些具有开放性、探究性的问题。为解决这类问题，教师不仅应引导学生深入分析，还应渗透优化思想，让学生体会数学问题解决策略的多样化，从而建构数学模型。

例如，人教版四年级上册“烙饼问题”一课的教学目标之一就是让学生学会运用优化思想构建解决数学问题的思维模型。教学这一内容时，教师先出示情境图：“星期天，王阿姨来到小丽家做客，妈妈准备做最拿手的烙饼当点心吃，谁来说说，从这幅图中你得到了哪些数学信息？”教师利用情境图，唤醒学生有关“烙饼”的生活经验。生活经验丰富的学生，马上想到饼的两面都需要烙。然后，教师出示问题：“每次最多只能烙两张饼，两面都要烙，如果要烙两张饼，怎么样才能尽快吃上饼？”对于“烙两张饼”所需的时间，学生说出两个答案：12分钟和6分钟。由于数字较小，教师用列举法来帮助学生理解。此外，教师还用图示法来演示：用课件出示一个锅，再出示2张饼;同时，教师把一个纸锅粘贴在黑板上，又拿出两个小圆片当成饼让学生上台演示“烙两张饼”，先烙两张饼的正面，后烙两张饼的反面，一共烙了两次，需要6分钟。

在此基础上，教师引导学生比较6分钟和12分钟两种烙饼方法，学生一致认为6分钟的烙法充分利用了锅内的空间，节省了时间，两张饼同时烙，就是最优方法。教师要重视启发学生主动收集数学信息，使学生通过观察、比较、分析、概括等，在主动探索的过程中感受到问题解决策略的多样化，培养学生的数学建模能力，实现学生对数学知识的内化。

二、在问题解决中体会集合思想，培养学生数学思维能力

数学知识具有较强的抽象性和逻辑性，教师要结合学情，巧妙创设情境，培养学生数学思维能力，使学生在解决数学问题的过程中体会数学思想[1]。

例如，在教学人教版三年级上册“数学广角——集合”时，教师创设情境：三（2）班同学在迎元旦联欢会上有5人参加合唱表演，有6人参加小品表演，参加这两项表演的一共有多少人？接着，教师利用课件出示三（2）班参加这两项表演的学生名单的统计表，在统计表中用序号表示学生的座位号，让学生观察参加这两项表演的总人数。

在反馈方法这一环节，出现了四种方法。

【方法一】          【方法二】

合唱：翁艳青、翁燕燕、张宇

小品：叶飞露、叶元浩、蔡秀婷、陈依星

两项都参加：翁家月、林凯宇

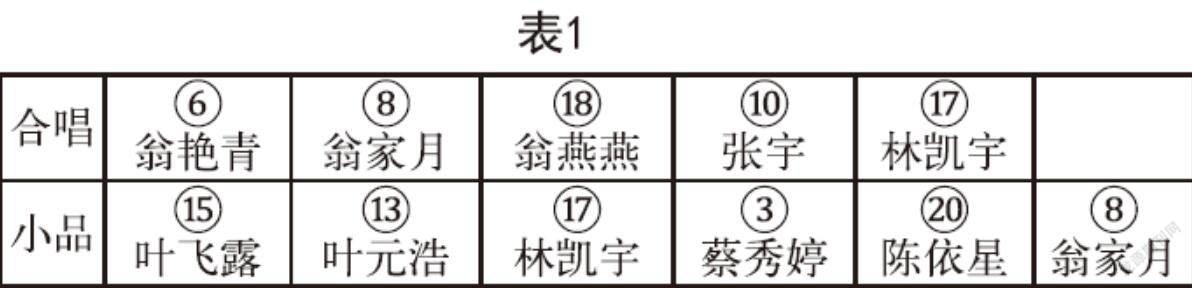
【方法三（见表1）】

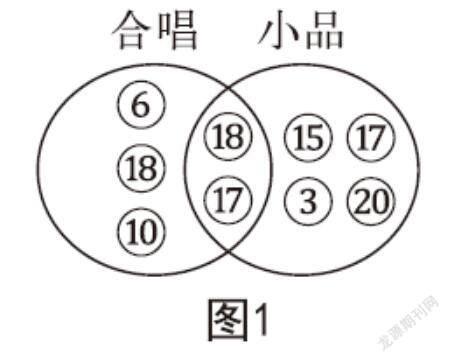
【方法四（见图1）】

这几种方法中，学生最喜欢方法四，因为这种集合图能直观看出参加各项表演的人数，特别是同時参加两项表演的人数，结果一目了然。本节课教学中，多样化的问题解决策略为集合思想的引入及学生思维能力的培养提供了良好的素材。

三、在问题解决中体会数形结合思想，培养学生分析比较能力

在教学中，教师可以通过让学生观察图形，培养学生数形结合思想，让学生借助直观的图形语言学习数学知识，从而培养学生分析比较的能力。

例如，在教学人教版四年级下册“小数的大小比较”时，教师让学生反馈研究方法，学生用了以下三种方法，很直观地表现出不同小数的大小比较方法。

（1）直线比较（见图2）

在直线上越往左边，数就越小，越往右边，数就越大。学生在直线上标出1.05与0.92的位置，发现右边的数大，所以1.05>0.92。学生在比较小数时用抽象的语言描述比较困难，利用数轴就能够很好理解。

（2）涂色比较

学生把两个相同的正方形都平均分成100份，其中一个正方形涂了88份，另一个正方形涂了92份，得出0.88<0.92。

（3）数位顺序表比较

教师让学生通过换算单位来理解，把0.88米与0.86米填入数位顺序表中。0.88米表示8分米8厘米，0.86米表示8分米6厘米，所以0.88>0.86。

这三种方法是把数转化成图形来研究的，很直观。学生反馈第一种方法比较简单;第二种比较直观但涂色麻烦;第三种方法比较实用，也比较科学。在教学中，教师要让学生从不同角度运用不同的方法处理问题，通过不同的图形找到解决问题的多样化策略，体会数形结合的数学思想，从而培养学生分析比较的能力，提高学生的问题解决能力和创新能力。

四、在问题解决中体会类比思想，培养学生数学运算能力

很多数学知识点存在一定的内在联系，教师要充分挖掘教材，让学生发现同一类型问题的解题方法非常相似，进而体会类比思想，在计算教学中发现运算的价值，发展数学运算核心素养。

例如，在教学人教版三年级上册“三位数加三位数的连续进位加法”时，教师先创设情境：“羊村举行运动会，在比赛吃青草时，懒羊羊吃了465克青草，喜羊羊吃了398克青草。你能提出哪些数学问题？”教师根据学生的回答挑选出一个问题：它们一共吃了多少克青草？然后，教师让他们用三种方法进行计算。

（1）估算

教师让学生先来估算一下，因为465最接近470， 398最接近400，所以465+398≈870（克）。

（2）口算        （3）笔算

398接近400，可以    465+398=863（克）

看作400来口算。

465+398

=465+400-2

=865-2

=863（克）

在笔算时，学生可以类比两位数的连续进位加法，验算时可以交换465和398的位置，再算一遍。

最后，教師让学生讨论各种算法。学生认为，估算不能得到准确答案，口算有时会出错，用竖式进行笔算能培养认真进行计算的习惯，可以使计算做到又对又快。在教学三位数的连续进位加法笔算时，教师可以让学生类比两位数的连续进位加法笔算的方法，并且交换位置进行验算，从而培养学生的数学运算能力。

结  语

总之，在小学数学教学中，教师要积极渗透优化、集合、数形结合、类比等数学思想，培养学生从多层面分析和解决数学问题的能力。在教学实践中，教师要让学生感悟解决问题的多样策略，培养学生各方面的能力，从而发展学生的核心素养，为学生的终身学习打下良好的基础。

[参考文献]

[1]邵陈标.“分数的初步认识”教学同课异构及反思[J].辽宁教育，2007（12）：56-59.

作者简介：郭雪琼（1983.11-），女，福建莆田人，本科学历，一级教师，莆田市小学数学骨干教师，区教坛新秀、区优秀班主任，多次参与省、市、区级课题研究。