电力变压器三维瞬态漏磁场及电动力仿真分析

2021-01-16穆龙陈伯根蔡锋吴丽明杜国安兰生

哈尔滨理工大学学报 2021年5期

穆龙陈伯根蔡锋吴丽明杜国安兰生

摘要：为了分析变压器绕组在短路冲击下的瞬态磁场及瞬态电动力特性，依据变压器绕组的漏磁场理论和短路电动力的计算原理，利用计算电磁场的有限元分析软件，以1台SSZ11-50000/110三绕组电力变压器为研究对象，建立了变压器绕组的仿真模型和短路计算方程，进行了变压器瞬态漏磁场和瞬态短路电动力计算仿真分析。在变压器高中运行方式的中压侧绕组出现接地短路故障时，计算出绕组瞬态漏磁场，以及绕组轴向、辐向瞬态短路电动力的分布规律。仿真结果表明，绕组在短路过程中，漏磁场、电动力分布与时间和空间有关，并均在t=0.01s时刻出现最大值。在任意时刻下，轴向磁感应强度，两侧小，中间大;中压和高压绕组之间的辐向磁感应强度近似为“A”形。铁芯窗内侧与铁芯窗外侧绕组的辐向电动力的分布规律不同，辐向电动力铁芯窗内侧比铁芯窗外侧数值大。绕组轴向电动力，近似中心对称分布，均表现为两侧电动力数值最大，靠近绕组中部最小。此研究为防止变压器绕组变形和改进设计提供参考。

关键词：电力变压器;三相短路;瞬态电动力;有限元仿真

DOI：10.15938/j.jhust.2021.05.014

中图分类号：TM41 文献标志码：A 文章编号：1007-2683（2021）05-0104-10

0 引言

电力变压器是电力系统中重要的设备，由于电力系统的短路电流过大、绕组设计不合理等原因，不同型号的变压器多次出现绕组扭曲、变形、松散、导线折断等结构损坏的情况。目前，变压器绕组检修周期长、检修难度大，给电力系统的运行维护工作造成极大困难，因此有必要从变压器绕组设计的初始阶段对绕组进行抗短路能力设计[1-2]，降低变压器绕组事故率。变压器绕组变形的机理复杂，提升变压器绕组的抗短路能力，需要加强对绕组在短路条件下的短路电动力的研究，并根据电动力的分布规律，有针对性的改善结构强度，显得十分重要。

国内外研究人员对于电力变压器短路电动力已经做了大量研究。闫振华等运用有限元对变压器电磁一结构耦合计算，并运用动力学原理，研究短路电磁力作用下的低压绕组机械强度及变形过程[3]。Ahn等搭建三维有限元模型，利用了短路电流作为直接激励，计算了变压器绕组的电动力分布和动态形变量[4-5]。刘文里等利用ANSYS有限元软件计算了绕组电动力，建立低压绕组的单层结构模型，结合屈曲分析方法分析了低压绕组的辐向稳定性[6-7]。刘军等使用有限元计算和理论计算的方法，对不同型号的变压器的抗短路能力和绕组的稳定性进行理论校核，并总结了变压器绕组稳定性的理论校核方法[8-10]。赵志刚等计算了变压器磁场，并把理论计算结果与220kV变压器的突发短路试验结果作对比，分析了变压器低压绕组辐向宽度、导线尺寸、撑条等对变压器抗短路能力的影响[11]。李德波等计算了变压器三相短路的情况下，绕组的瞬态轴向力和辐向力，得出了绕组最大时刻的电磁力分布规律[12-13]。张海军等利用有限元方法分析绕组累积变形的机理，计算了变压器绕组在多次累积冲击下的变压器绕组结构变化特点[14-15]。王丰华等使用有限元方法，分析不同预紧力、材料等因素影响绕组轴向的振动特性，并利用实验验证了相关理论[16-18]。汲胜昌等利用ANSYS软件对变压器绕组在稳态运行条件下的振动特性进行了仿真计算，并将结果同实测数据进行对比验证，分析了绕组轴向振动特性随其预紧力、温度、老化程度而变化的趋势[19]。

上述文献的成果为研究绕组稳定性和抗短路能力提升提供大量理论指导。然而，其中，一部分文献用二维有限元模型计算短路电动力的大小，着重研究绕组的结构动力学问题，校核电磁力大小。另外一部分文献，利用变压器三维模型仿真，将绕组用圆筒代替，未对绕组、铁芯进行细化，计算精度较低。并且，一部分研究集中于分析计算变压器绕组某一时刻的短路电动力和漏磁场的分布规律，或结合力學的基本理论，分析绕组某一时刻的稳定性特性。在实际的短路过程中，绕组的状态是不断变化的。由于绕组中短路电流的快速变化，短路电动力和漏磁场也是变化的，在整个短路过程中，短路电动力对绕组的影响应是短路电动力在时间和空间下共同作用的结果。研究绕组的动态力和动态磁场的分布规律，了解绕组磁场和电动力在空间和时间上的分布规律，对研究和分析绕组结构强度变化有一定的参考意义。

本文利用1台SSZ11-50000/110的三相变压器为计算实例，根据绕组的几何参数，把绕组1层分为1个线饼，其中，高压绕组分为74个线饼，线圈总匝数为518匝，中压绕组分为92个线饼，线圈总匝数184匝;同时，也充分考虑了变压器实际铁芯的构造，对铁芯进行分层三维建模，分析了变压器绕组轴向和辐向不同空间位置的瞬态漏磁场和不同线饼轴向和辐向瞬态电动力分布规律。

1 变压器漏磁场和电动力计算

1.1 绕组漏磁场计算原理

在短路情况下，变压器的短路电流迅速增加，短路电流的幅值是额定电流的数十倍，当变压器中流过负载电流时，会在绕组及其周围产生磁通，一般把在绕组及其周围产生的磁通称为漏磁通。变压器漏磁场是一个含有多介质、非线性的三维瞬态涡流场问题，工程计算一般引入了矢量磁位A和标量电位Φ，由Maxwell方程组，并引入库仑规范，推出计算变压器绕组的瞬态磁场方程式[20]：

1.2 短路电流的计算

变压器出口处发生三相短路时，短路电流值最大，此时绕组的电动力最大，进行变压器短路电动力计算，应按照变压器出现最严重的三相短路情况考虑。由于变压器的相间的对称性，变压器绕组的瞬态短路电流的计算原理相同，仅取三相中的一相进行分析。当变压器的二次侧发生短路时，等效电路图如图1所示，根据电路的原理，写出以电流为变量的微分方程：

也称为短路电流冲击系数。

1.3 电动力计算

在短路情况下，变压器绕组的漏磁场和短路电流的共同作用下，在某个时刻，根据磁势平衡原理，高中压侧的电流方向相反，绕组的短路电流在轴向产生磁感应强度Bz，在绕组内部短路电流的作用下，产生辐向的短路电动力Fr，使得中压绕组在短路电动力作用下向内压缩;高压绕组在短路电动力作用下向外拉伸。绕组的短路电流在辐向产生磁感应强度Br，在绕组内部短路电的作用下，产生轴向的短路电动力Fz，使得高、中压绕组均受到两端向内的挤压力，示意图如图2所示。

根据电动力计算原理，绕组受力方向通常分为辐向分量和轴向分量，由式（6）可推出（12）式，分别得到绕组辐向分量Fr和轴向分量Fz：式中：Fr，Fz分别为辐向和轴向电动力;Jτ为电流密度;V表示绕组线饼载流导体的体积。

转换到直角坐标系下，洛伦兹力的3个分量和合力如式（13）：

2 仿真的实例分析

2.1 仿真模型建立

本文以1台型号为SSZ11-500001110电力变压器为例，考虑高中运行方式下，三相电力变压器的各相对称，为了简化计算，只考虑三相中的B相，并根据表1电力变压器的结构参数、表2电力变压器的电气参数，建立三维的有限元仿真模型，如图3所示。电力变压器有限元模型的高压、中压绕组用套筒式组合，高压、中压绕组由线饼叠加而成;铁芯用硅钢片分层叠加，在不改变几何尺寸的前提下，适当减少层数。

为了减少有限元仿真的计算量，研究做出了如下假设：

1）不考虑变压器的油箱、油道的影响，绕组外部用油介质区域代替;

2）不考虑变压器绕组垫块、压板、夹件、撑条，保留线饼与线饼的间隙;

3）由于变压器三相对称，故只对其中一相建模，并忽略绕组相间的影响。

在仿真计算过程中，高压绕组侧加载电压，中压绕组侧短路，低压绕组侧开路，三相三绕组模型简化为了1个三相双绕组变压器，仿真只涉及到计算高压、中压绕组的短路电动力和磁场。仿真的激励是通过公式（10）计算而得到的高、中压绕组的短路电流ih-k、im-k，其表达式分别为式（14）、（15）：

由式（14）、（15）可得到短路電流波形如图4所示，当t=0.01s时，高压、中压绕组的电流都达到最大值，高压绕组电流的最大值6804.5A，是额定电流的25.9倍，中压绕组电流的最大值是-18630.5A，是额定电流的24.8倍，高、中压电流方向相反，符合磁势平衡原理，证明短路电流的计算值可靠。

计算模型的材料属性主要设置绕组铜的电导率、铁芯的磁化特性曲线、绕组所处空间的介质特性等。其中，变压器的铁芯采用冷轧硅钢片35DQ151，绕组铜线的电导率2.10×10-8Ω·m，变压器油介质的相对介电常数为2.20，其他材料参数根据设计参数选取。

磁场计算过程中，网格的质量决定了计算的准确性。ANSYS Maxwell有自适应剖分和手动剖分两种形式，本文采用自适应剖分，对不同模块控制网格的最大边长进行剖分。其中，高压、中压绕组最大网格边长为3mm，铁芯最大网格边长为5mm，变压器油介质所在空间区域的最大边长为10mm，自适应的网格总数量为10305263个，能量迭代误差变化率为1.30%，网格总体质量较好。

2.2 漏磁场计算结果

利用ANSYS Maxwell进行有限元瞬态磁场仿真，从仿真结果中，取t=0.01s的磁感应强度计算结果如图5所示。由于绕组所在空间油介质的作用，绕组的磁感应强度相对于铁芯的磁感应强度较小，绕组中的磁感应强度分布比较均匀，其平均值为1.36T。

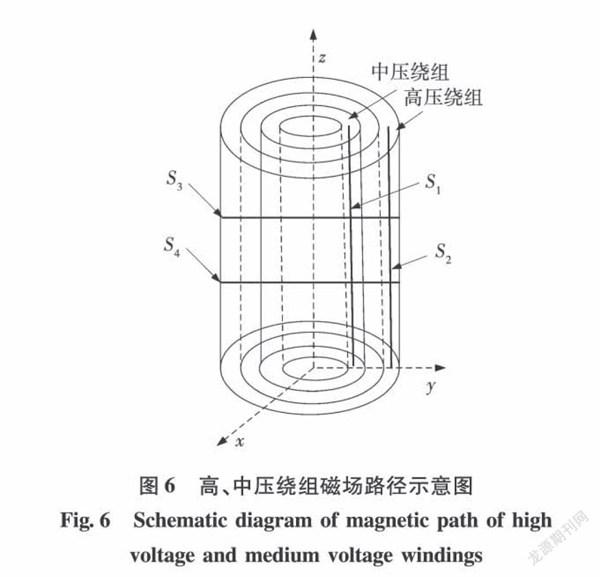
为了区分绕组不同方向的磁场分布，把变压器磁场分布方向主要分为轴向和辐向两个方向。如图6所示，沿着高压、中压绕组轴向分别选取路径S2、S1，计算相应绕组瞬态磁场分布如图7和图8所示。高压、中压绕组的轴向瞬态磁场，二者与电动力的波形相似，第一个峰值是频率为f的暂态周期分量，并随时间逐渐衰减，第二个峰值是频率为2f稳态周期分量，并随时间逐渐增大。在不同时刻下，由于绕组的端部有辐向漏磁分量，使相应的轴向漏磁分量变小，导致绕组轴向磁场近似为“梯形”分布，数值不同。

按示意图5所示，选取高压、中压绕组的辐向选取两个路径S3、S4，路径S3、S4穿过绕组和绕组中的气隙，利用有限元求解该路径下的磁感应强度分布规律如9、10所示。

对比图9和图10，路径距离为0～200mm和1200～1400mm的位置出现最大值，由于S3、S4路径穿过绕组之间的主空道，最大值出现在主空道，近似为“”形，中压绕组磁感应强度从内侧到外侧逐渐增大，高压绕组磁感应强度从内侧到外侧磁场强度逐渐减小。其中，中压绕组外侧和高压绕组内侧磁场强度最大，相应绕组电动力最大。

同一时刻下，S3、S4路径下辐向磁感应强度均呈对称分布，两个绕组之间的空道中的辐向磁感应强度最大;同时，由于中压绕组中间的空道位于绕组与铁芯、气隙的空间之中，磁阻大，辐向磁感应强度分布平均，总体分布始终最小。

2.3 瞬态短路电动力的分布

通常情况下，考虑到继电保护设备在故障发生0.1s左右动作，本文计算的瞬态绕组短路电动力的大小仅考虑0.1s范围内的波形变化情况。为了便于区分不同位置的短路电动力的波形，本文将高压绕组的74个线饼分别标记为1号、2号、…、74号，将中压绕组的92个线饼分别标记为1号、2号…、92号，得到6种不同种类的时间一线饼一电动力三维分布图。

图11、图12分别是高、中压绕组轴向短路电动力的分布图，轴向电动力的方向对应图5中z轴方向，瞬态电动力变化规律与磁感应强度变化趋势一致，变化的频率相同，分布规律相似，均在t=0.01s达到最大值，随后出现衰减。当t=0.01s，高压绕组和中压绕组电动力出现最大值，高压绕组的最大短路电动力为1.920×105N，中压绕组的最大短路电动力1.250×105N。同一时刻下，高、中压绕组两端至中部绕组线圈的轴向电动力，呈现逐渐减小的趋势，靠近绕组中间附近位置数值相差较小。其中，高压绕组1～10号、60～74号线饼和中压绕组1～20号、80～92号线饼轴向电动力较大，方向相反，近似呈中心对称分布，轴向电动力从两侧向中间挤压绕组，与上述原理分析相符合。

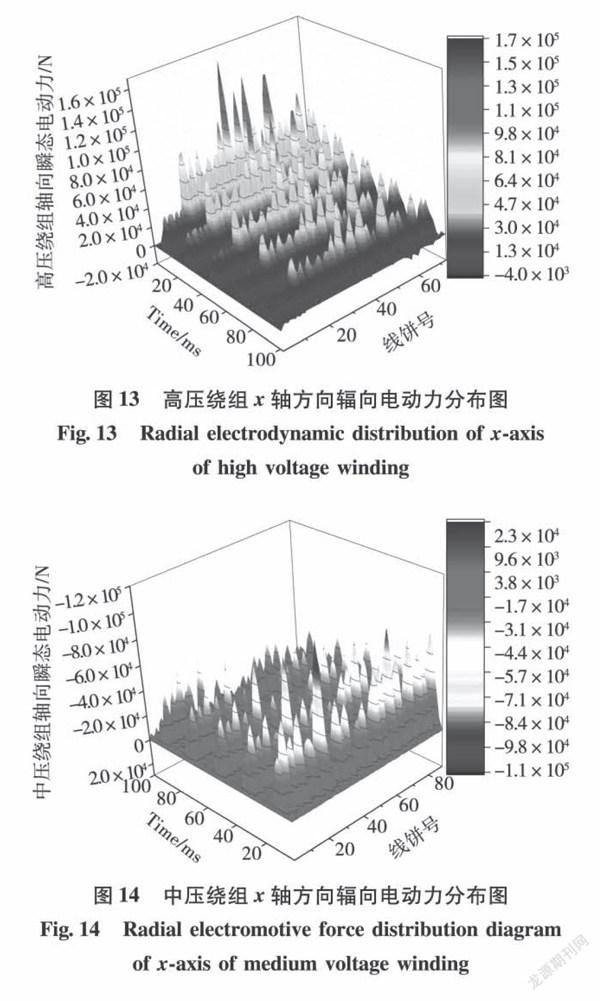
变压器绕组辐向电动力的计算，考虑对应图5所示的x、y两个不同方向。其中，x轴方向靠近相邻绕组铁芯窗口的内侧，y轴方向垂直于铁芯窗口的外侧，x、y方向的合力共同作用于绕组，使绕组内径扩大或缩小。图13、图14分别选取高、中压绕组靠近铁芯窗内侧的x轴辐向电动力，高压绕组辐向最大短路电动力是1.66×105N，中压绕组的辐向最大短路电动力是-1.1×105N。整个短路过程中，高压绕组和中压绕组的辐向电动力总是中间部位大，两侧小，二者方向相反，高压绕组辐向电动力方向为正，向外侧拉伸，中压绕组辐向电动力方向为负，向内侧压缩。

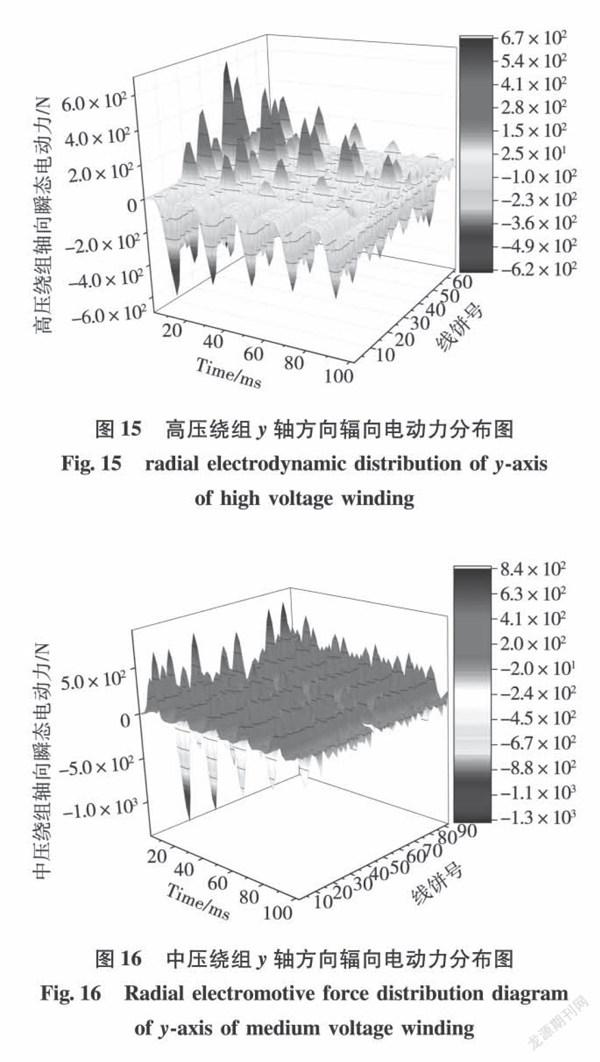
图15、图16分别选择靠近高、中压绕组的铁芯窗外侧的y轴方向进行分析，y轴方向的辐向电动力方向并不完全一致向内或者向外，辐向电动力的数值相比铁芯窗内侧绕组更小。其中，高压绕组y轴方向辐向电动力整体方向为负，靠近中间位置的20～40号线饼的电动力方向为正;中压绕组y轴方向辐向电动力整体方向为正，部分线饼电动力方向为负。绕组的不同线饼，不同辐向存在拉伸力或压缩力的同时作用，绕组辐向合力作用方向不同，在轴向力的同时作用下，绕组受到倾斜向上或向下的合力，增加绕组发生扭转变形的可能。

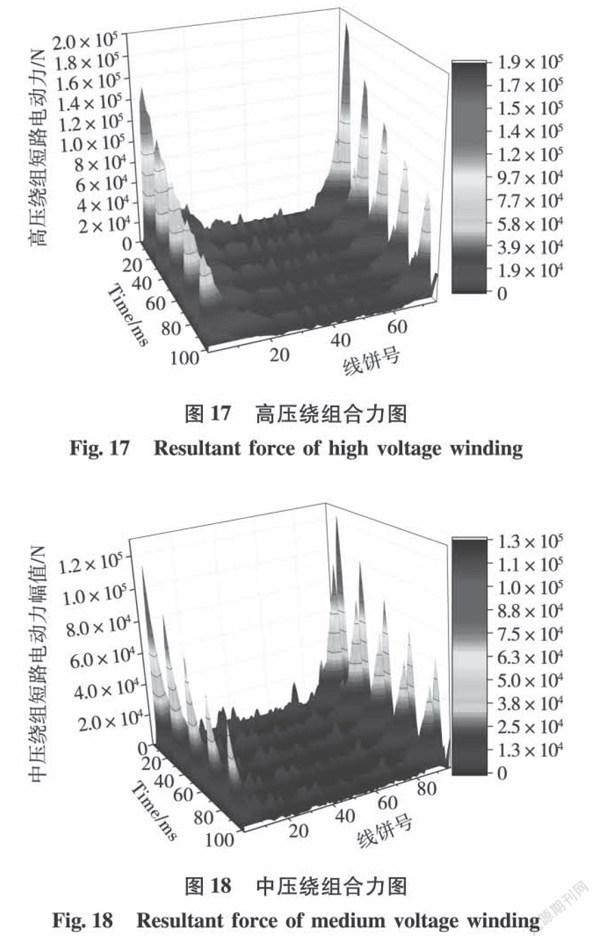
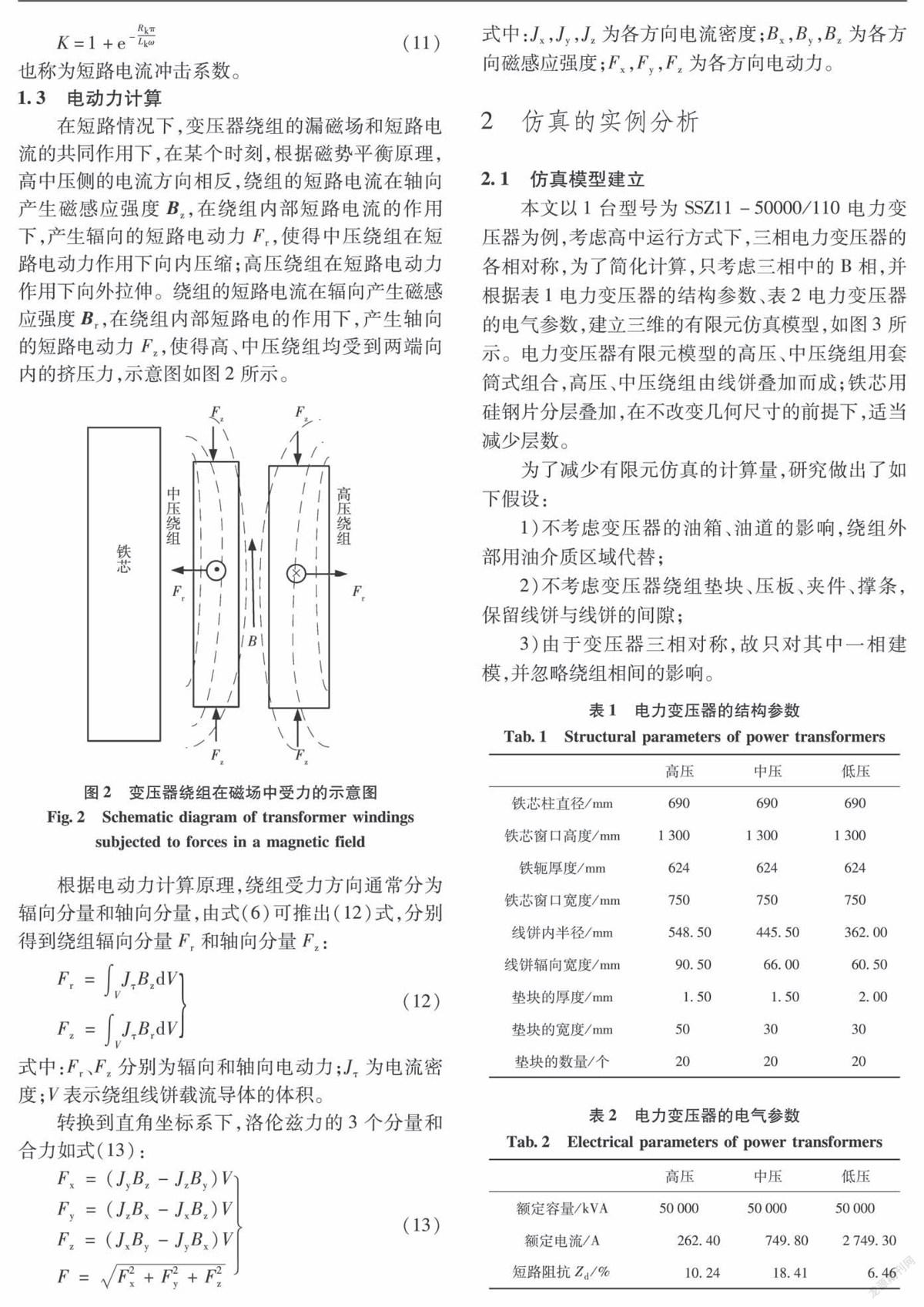
如图17、图18所示，高压绕组1～20号、60～74号线饼所受的短路电动力合力较大，此区域最大短路电动力为1.930×105N;中压绕组10～20号、80～92号线饼受到的短路电动力合力较大，此区域最大短路电动力1.250×105N。1～20号、60～74号、10～20号、80～92号均靠近绕组的两侧，两侧电动力最大，向中间挤压绕组，辐向电动力向内或向外拉伸，加剧绕组变形。当绕组受到的合力越大，整体的形变越严重，绕组越容易出现塑性形变。

在整个短路电流衰减的过程中，高压和中压的瞬态合力保持衰减趋势，两侧的电动力平缓衰减，波形相似，绕组中间部位均数值最小。从绕组电动力分布规律可知，两侧电动力较大，中间电动力较小，两侧向中间挤压绕组，在轴向和辐向的共同作用下，高、中压绕组中间部位容易出现凸起、凹陷故障。从提升绕组的抗短路能力角度考虑，绕组的薄弱区域应该避免绕组的导线上下换位、更换强度更好的撑条、施加合适的预紧力等措施，使绕组的整体抵抗短路电动力的能力提高。

3 结论

本文研究了电力变压器绕组在三相接地短路条件下，绕组瞬态漏磁场和瞬态短路电动力的分布规律。通过使用ANSYS Maxwell有限元仿真软件，并结合一台110kV电力变压器作为仿真实例，分析得到时间-线饼号-电动力和時间-线饼号-磁感应强度分布规律图。仿真结果显示：

1）绕组的同一线饼，变压器绕组的瞬态磁感应强度的频率和瞬态电动力的频率相同，且绕组轴向和辐向之间的电动力、磁场相对独立，数值大小不同，波形变化规律基本相似。

2）在任意时刻下，轴向磁感应强度在绕组两侧数值小，在绕组中间磁感应强度数值大;中压绕组辐向磁感应强度从内侧到外侧逐渐增大，高压绕组辐向磁感应强度从内侧到外侧磁场强度逐渐减小，高压和中压绕组之间的空道磁场强度最大，铁芯与绕组之间的空道磁场平均分布，数值较小。

3）短路过程中，绕组的不同线饼，靠近铁芯窗内侧x轴方向的辐向电动力，高压方向为正，绕组向外拉伸，中压绕组方向为负，向内压缩;绕组的不同线饼，靠近铁芯窗口外侧Y轴方向的辐向电动力的方向不完全相同，有正有负，部分线饼的电动力出现最大值。高压和中压x轴方向的辐向电动力比Y轴方向的辐向电动力大，应该加强绕组x轴方向的强度。

4）高压和中压绕组轴向短路电动力频率相同，波形变化趋势相似，任意时刻绕组轴向电动力近似中心对称分布，高压和中压绕组均表现为两侧电动力数值最大，靠近绕组中部最小。

5）当t=0.01s，随着短路电流出现最大值，其轴向和辐向的瞬态短路电动力、瞬态漏磁场数值均为最大值，此时电动力对绕组的垫块、撑条的考验巨大。

上述研究的结论，对于研究绕组轴向和辐向稳定性以及绕组的形变情况，有一定的借鉴意义。

参考文献：

[1]张春红，周腊吾，李中祥，等.一起500kV事故变压器短路强度计算与分析[J].变压器，2016，53（3）：1.

[2]宋云东，周志强，张文广，等.一起变压器绕组严重变形缺陷分析[J].变压器，2019，56（8）;79.

[3]闫振华，马波，马飞越，等.220kV电力变压器短路电动力学性能分析[J].高压电器，2014（3）：79.

[4]AHN H M，LEE JY，KIM J K，et al.Finite-Element Analysis ofShort-Circuit Electromagnetic Force in Power Transformer[J].IEEE Transactions on Industry Applications，2011，47（3）：1267.

[5]ZHANG H，YANG B，XU W，et al.Dynamic Deformation Analy-sis of Power Transformer Windings in Short-Circuit Fault by FEM[J].IEEE Transactions on Applied Superconductivity，2014，24（3）：1.

[6]兰生，胡忠平，廖福旺，等.短路电动力对变压器低压绕组辐向稳定性的研究[J].电机与控制学报，2018，22（5）：19.

[7]刘文里，唐宇，李赢，等.电力变压器高压绕组辐向稳定性评估[J].哈尔滨理工大学学报，2016，21（4）：90.

[8]刘军，张安红.电力变压器绕组短路动稳定能力的仿真和评估[J].变压器，2012（6）：14.

[9]郑含博，翟进乾，李哲，等.大型电力变压器内绕组辐向抗短路能力评估[J].电力系统保护与控制，2016，44（22）：154.

[10]王鹤许.电力变压器抗短路能力校核方法的研究[D].北京：华北电力大学，2013.

[11]赵志刚，李光范，李金忠，等.基于有限元法的大型电力变压器抗短路能力分析[J].高电压技术，2014，40（10）：3214.

[12]李德波，张波，臧春燕，等.电力变压器绕组短路瞬态受力析[J].高压电器，2019，55（1）：87.

[13]刘凡，姚成果，陈凌，等.基于有限元法电力变压器绕组的短路电动力分析[J].电测与仪表，2016，53（4）：113.

[14]张海军，王曙鸿，李姗姗，等.多次短路下电力变压器绕组变形累积效应分析[J].变压器，2018，55（2）：37.

[15]张博，李岩.多次冲击条件下的大型变压器绕组辐向失稳[J].电工技术学报，2017，32（z2）：71.

[16]王丰华，杨毅，何苗忠，等.应用有限元法分析变压器绕组固有振动特性[J].电机与控制学报.2018，22（4）：51.

[17]李洪奎，李岩.不同预紧力下变压器绕组轴向振动模态分析[J].电机与控制学报，2010（8）：101.