CFRP加固圆形钢管抗压承载力研究

2021-01-16高小育杨正朴李兆阳刘永健

建筑科学与工程学报 2020年6期

高小育，段海，杨正朴，李兆阳，刘永健

(长安大学公路学院，陕西西安 710064)

0 引言

传统的钢结构或者构件的加固方法主要包括螺栓连接、焊接、粘钢加固等[1]。这些加固方法所带来的焊接残余应力、截面削弱、应力集中等诸多问题是不容忽视的。碳纤维增强复合材料(Carbon Fiber Reinforced Polymer，CFRP)由于具有足够大的刚度、优越的抗腐蚀和抗疲劳性能以及加固施工工艺上的诸多优势，能够很好地弥补传统钢结构加固方法的不足[2-3]。现有的关于CFRP粘贴加固钢结构的理论及试验研究大多集中在梁的受弯加固[4-6]、疲劳加固[7-8]、轴压短柱加固[9-10]以及CFRP与钢材之间界面性能研究[11-12]等，而关于CFRP加固长钢管轴压构件的研究开展较少，因此进一步研究CFRP加固长钢管的轴压性能，分析CFRP的受力机理，提出一种较为可靠的研究此类加固构件轴压承载力及变形的方法是十分必要的。

目前已有的试验初步表明CFRP可以有效增强受压钢管的承载力[12-17]。CFRP加固长钢管轴压性能的研究通常采用数值分析方法，Shaat等[18]、彭福明等[19]、魏劭杰等[20]分别采用纤维模型法、ANSYS、ABAQUS有限元软件对CFRP加固轴压构件进行了模拟。现有研究鲜有对CFRP的受力状态及加固机理做具体分析。同时由于CFRP的特殊性，如脆性破坏、材料的各向异性、抗拉抗压力学性能的差异性以及CFRP与钢材之间复杂的界面行为等，都给数值模拟带来很大的障碍，不利于此类构件的研究应用。因此，本文欲依托CFRP加固长圆形钢管轴压试验结果，对CFRP的受力状态进行分析并提出一种CFRP加固长圆形钢管轴压承载力的简化计算方法。

1 试验概况

试验分为5组，包括1个钢管对照组和4个分别包裹2，4，6，8层CFRP布的对照组。钢管外径为88.9 mm，壁厚4 mm，屈服强度及抗拉强度分别为355 MPa和490 MPa，每根钢管的截断长度为2.4 m。加固钢管外包高模量的CFRP(MBRACE CF 130)，加固方式采用纤维方向沿钢管长度方向粘贴。在粘贴CFRP之前，钢管表面需预先粘贴1层GFRP(MBRACE ED 900)以防止碳纤维与钢管直接接触发生电化学腐蚀[21]。各层CFRP以及纤维与钢管之间均采用环氧树脂黏结。FRP与环氧树脂材料特性见表1。

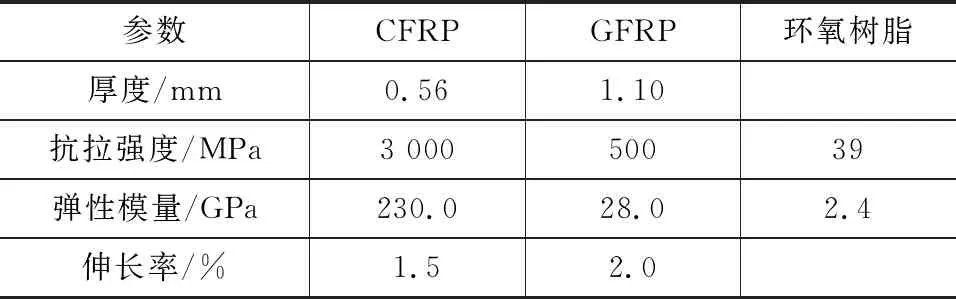
表1FRP和环氧树脂材料特性Tab.1Material Properties of FRP and Epoxy

钢管的轴压试验在1 000 kN液压试验机上进行。钢管底端采用光滑的半球形铰支座以保证钢管端部的自由转动，如图1(a)所示。为记录加载过程中钢管产生的位移，试验构件两端及中点分别安装4个LVDT位移传感器来记录端部的轴向位移及中点的横向位移，如图1(b)，(c)所示。同时在钢管中点处竖向对称粘贴长度为10 mm的电阻应变片(S1，S2，S3，S4)以记录构件中点的纵向应变。

图1试验装置Fig.1Test Setup

通过试验观察发现，受压构件在加载初期就开始产生侧向挠度。随着荷载的增加，受压构件侧向挠曲变形逐渐增大，当荷载达到某一数值以后，受压构件首先出现整体失稳，挠曲变形急剧增大，继而在构件中部截面附近压力较大侧发生局部失稳，受压构件丧失承载能力。对于CFRP加固的构件，局部失稳区域出现CFRP的脱层和压溃。在结构出现整体失稳前，跨中均处于压应变状态，局部失稳后，受压构件一侧出现压应变，其他部分仍表现为压应变。试验中还发现，随着粘贴CFRP层数的增加，相同荷载下钢管的轴向位移和侧向位移均减小。各受压构件轴向承载力结果如表2所示。

表2构件轴向承载力Tab.2Axial Bearing Capacity of Specimen

2 CFRP的稳定性分析

2.1 CFRP加固钢管增强受压承载力机理

周雷等[22]的试验展示了2种碳纤维复丝的受压破坏模式，分别为整体剪切破坏和基体失效后的局部剪切破坏，试验中的构件并不是由于抗压强度过大引起失效。即便如此，碳纤维复丝的抗压破坏强度依旧超过了2 000 MPa，表现出了优异的抗压性能。试验现象表明，在构件失稳之前CFRP处于受压状态，构件承载力的提高主要源于CFRP自身的抗压稳定性。关于CFRP在轴压构件上表现出的抗压能力，本文给出以下解释：①CFRP在使用前经过环氧树脂的浸渍，环氧树脂加强了纤维束的整体性，使之在受力过程中可以共同工作，从而产生了一定的抗压强度；②CFRP对圆形钢管加固后，包裹在钢管表面，其形状由片状变为圆筒(图2)，刚度得以提高，进而增加了碳纤维布的抗压稳定性；③钢管外表面的CFRP类似于薄壁圆筒，钢管对CFRP起到径向支撑作用(图3)，限制了CFRP的局部屈曲，进一步提高了其整体稳定承载力。基于以上3个解释，CFRP加固钢管后，由于CFRP本身具有抗压能力，CFRP可以在构件受压时承担一部分荷载。同时，钢管与CFRP之间的支撑作用是相互的。CFRP同样可以对钢管形成约束，减少钢柱的侧向位移，使得钢管受压更加均匀，钢管在荷载更大时开始出现塑性。

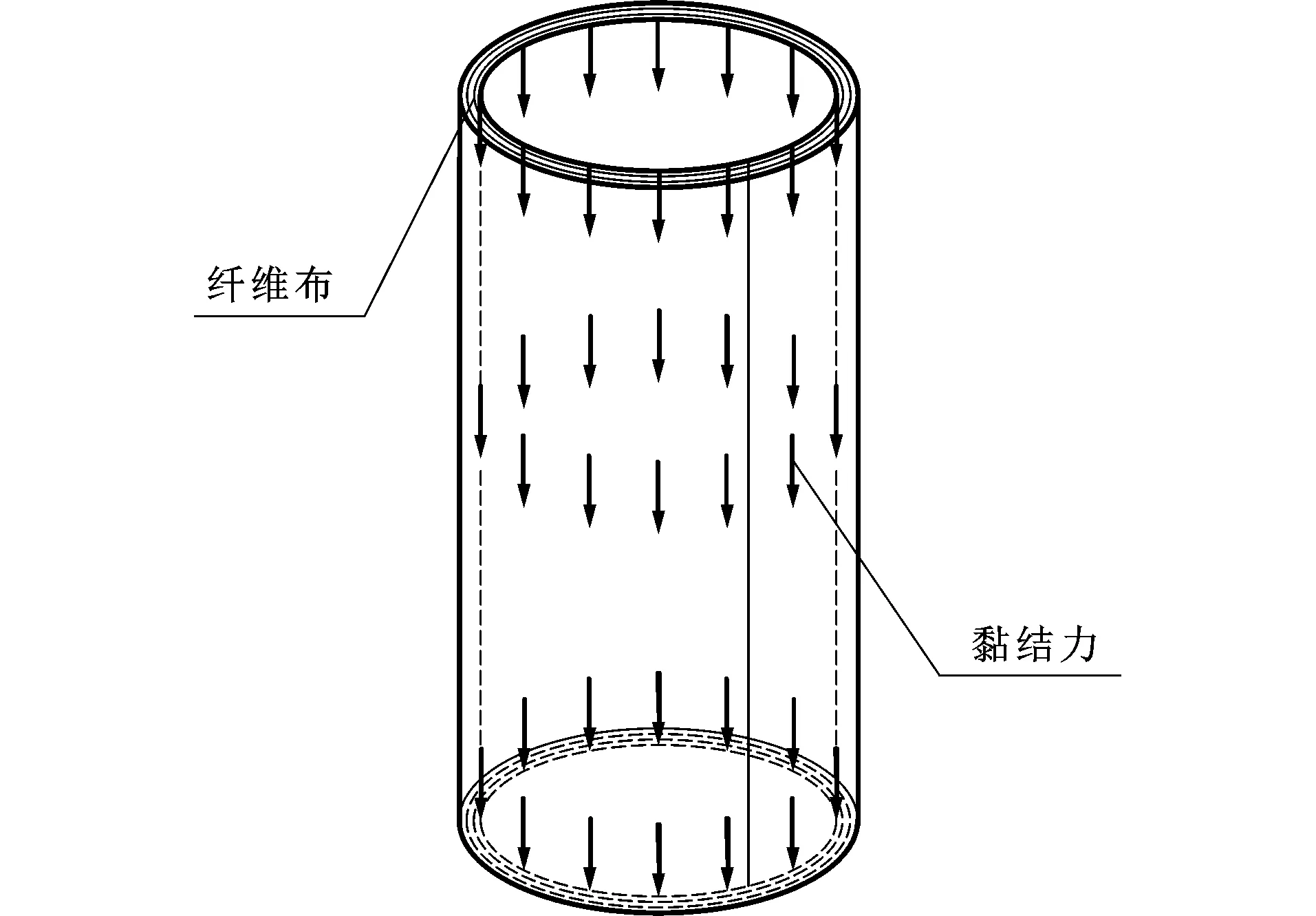
图2CFRP形成圆筒Fig.2CFRP Becoming Cylinder

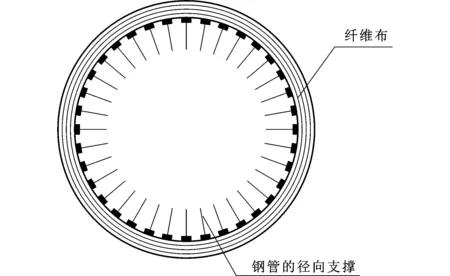
图3钢管对CFRP的径向支撑作用Fig.3Radial Support Effect of Steel Tube on CFRP

2.2 加固机理的力学模型简化

对于CFRP加固钢管轴压构件问题，CFRP的受力状态比较复杂，在受力变形过程中，CFRP同时受到纵向、环向的拉力和压力等，为了便于计算和模拟，需对其受力状态进行简化。本文研究采用的简化包括：

(1)由于加固构件为长柱，纤维束沿钢管纵向粘贴，因此忽略CFRP对钢管套箍效应的影响，只考虑CFRP的纵向受力。

(2)根据试验所测得的荷载-应变曲线可知，在构件失稳之前各截面CFRP均处于受压状态，因此可忽略CFRP的纵向抗拉性能对加固构件稳定承载力的影响。

(3)通过试验现象发现，CFRP的受压或剥离破坏由钢管的局部失稳导致，这发生于整体失稳之后[13]。因此，在构件达到稳定承载力之前可不考虑CFRP的剥离破坏，只需考虑CFRP与钢管之间的滑移导致的抗压模量损失。

因此，本文研究的关键在于如何确定加固构件CFRP的有效抗压弹性模量，即考虑CFRP与钢管之间的滑移之后的模量。基于以上分析，本文借助纤维模型法对CFRP的有效抗压弹性模量进行了分析。

2.3 建立纤维模型

纤维模型将截面进行离散，模型像一束纤维，纤维之间通过平截面假定约束。假设每一纤维为单轴应力状态，因其受力状态类似于纤维，故称其为纤维模型。下文使用纤维模型对受压构件进行分析。

纤维模型中引入平截面假定。第i个单元的应变εi为

(1)

式中：hi为单元i距荷载偏心方向截面边缘的距离；c为中性轴距荷载偏心方向截面边缘的距离；ε为荷载偏心方向截面边缘应变值。

由于假定CFRP与钢管之间没有滑移，对于带有纤维层的截面，截面总有效惯性矩Iteff计算公式为

(2)

式中：Iseff为钢管的有效抗弯刚度；Ifeff为纤维复合材料的有效抗弯刚度；Efp为纤维的有效受压模量；Es为钢材的弹性模量。

假定钢为理想弹塑性材料，弹性模量为206 GPa。屈服强度为355 MPa。假定复合材料为理想弹脆性材料。由于纤维抗拉、抗压性能不同，纤维单元的应力σfi可分别通过σfi=Efpεfi或σfi=Eftεfi进行计算，其中Eft为纤维的抗拉模量，εfi为任一纤维单元应变值。当εfi>εut或εfi<-εup时，表示纤维已经破坏，即取σfi=0，εut，εup分别为纤维的极限抗拉、抗压应变值。

构件初始挠曲假定为半波正弦曲线，在轴压荷载P的作用下，构件将产生侧向挠曲变形，距压杆底端距离为z的截面横向位移δ可以通过公式(3)计算[18]，该式仅适用当δ≤L/10的情况。

(3)

式中：e′为杆件中点截面的初始偏心值；L为压杆的计算长度；Pcr为临界荷载。

构件加载端轴向位移Δ由材料压缩产生的轴向位移Δa和构件挠曲变形引起的轴向位移Δb两部分组成。Δa，Δb可分别由公式(4)，(5)计算，即

(4)

Δb=L-Δa-S

(5)

式中：Ei为第i个单元的弹性模量；Ai为第i个单元的面积；S为轴压构件变形挠曲线的弦长。

侧向挠曲线近似为弧长为L-Δa、振幅为δ+e′的半波正弦曲线。由此可以计算弦长S为

(6)

随着构件作用轴向荷载P的增加，跨中截面应变逐渐增大，钢单元逐渐屈服，直至跨中截面钢单元全部屈服，加载终止。此时构件具有较大的挠曲变形，横向位移δ的计算已不再适用公式(3)。

2.4 CFRP的抗压弹性模量

为排除各试验构件初始缺陷程度不同对研究结果的干扰，本文借助试验结果拟合所得的结论，运用加固构件稳定承载力与CFRP加固层数的线性关系，对回归方程进行线性插值，得到8个理论承载力[13]，并通过对轴压荷载设置初始偏心距来考虑构件的初始缺陷，偏心距按未加固钢管承载力取值。

在此基础之上，借助不同CFRP加固层数构件的理论承载力，利用纤维模型法分析CFRP抗压弹性模量的取值，得到如表3所示的计算结果。通过表3可以看出，CFRP的有效抗压弹性模量并不是恒定的，而是随着CFRP加固层数的增加而逐渐增大。

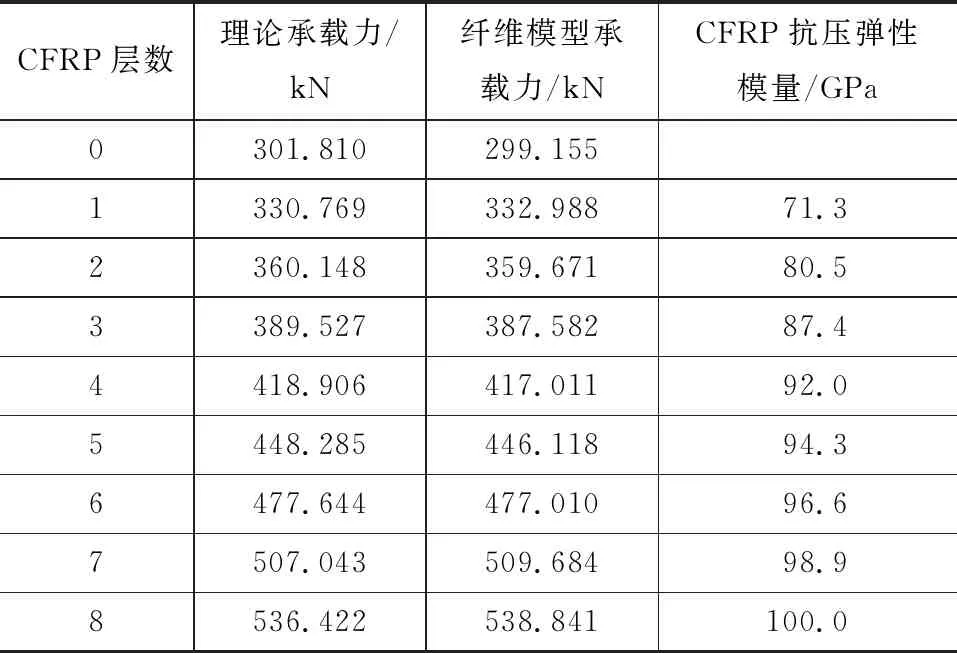
表3不同加固层数的CFRP抗压弹性模量Tab.3Compressive Elastic Modulus of CFRP for Different Reinforcement Layers

根据表3的计算结果，可得到CFRP抗压弹性模量与层数之间的关系曲线，如图4所示。

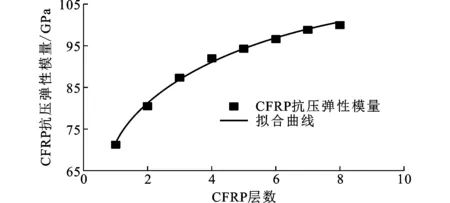
图4CFRP加固层数与抗压弹性模量关系曲线Fig.4Relation Curve of Reinforcement Layers and Compressive Elastic Modulus of CFRP

通过数值分析，可以得到抗压弹性模量和CFRP加固层数的关系为

Ecp=14.1ln(n)+71.4

(7)

式中：Ecp为CFRP抗压弹性模量；n为CFRP加固层数。

由式(7)可以得出：对于CFRP加固圆形钢管轴压构件，CFRP的抗压弹性模量随加固层数的增加按自然对数增长。

2.5 纤维模型计算结果

基于上述CFRP抗压弹性模量的分析结果，本文分别给出纤维模型法计算加固0，2，4，6，8层CFRP的构件的荷载-位移曲线，如图5所示。

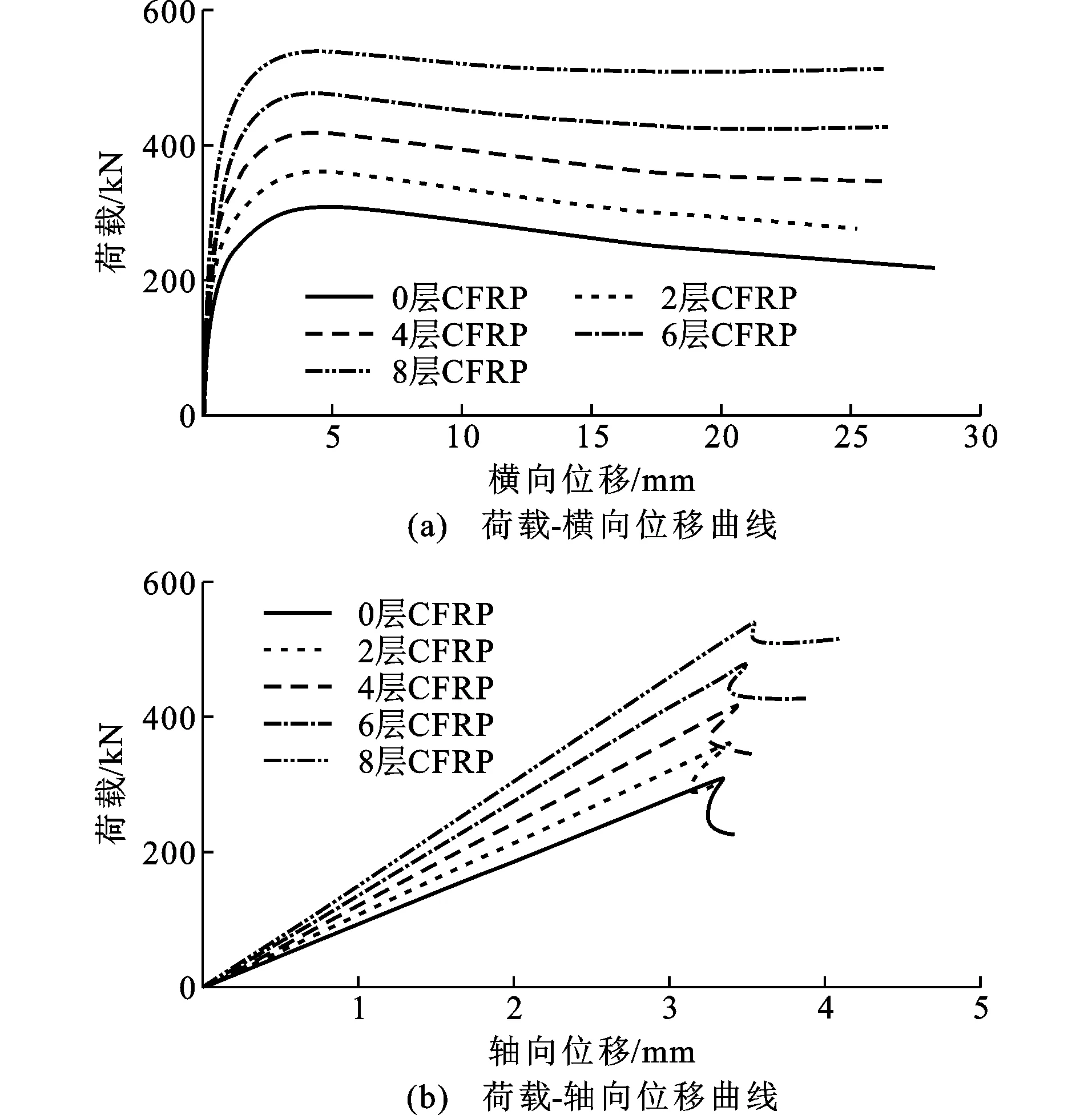
图5纤维模型荷载-位移曲线Fig.5Load-displacement Curves of Fiber Model

通过纤维模型可得到加固构件跨中截面荷载-应变曲线，应变计算点分别取为跨中截面偏心方向与垂直偏心方向截面外缘点。由于S1，S3沿偏心方向对称，因此两点应变值相等，故得到3条荷载-应变曲线。本文选取加固2，4层CFRP的钢管纤维模型为典型计算结果，荷载-轴向应变曲线如图6所示。

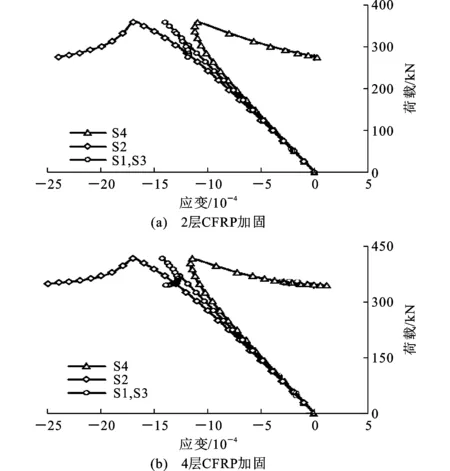
图6纤维模型荷载-轴向应变曲线Fig.6Load-axial Strain Curves of Fiber Model

由图6可以看出：纤维模型在其失稳之前，应变值均为负，即处于全截面受压状态；在达到稳定承载力之后，随着构件变形逐渐增大，跨中截面一侧开始出现拉应变，这与试验结果是一致的。

3 有限元模型

为了验证纤维模型及所获得的CFRP抗压弹性模量取值的正确性，本文通过ABAQUS通用有限元软件，基于上述CFRP受力状态的分析，对加固构件进行了模拟。

3.1 模型建立

钢管模型采用连续均匀实体单元C3D8R进行建模，为了限制线性缩减积分单元沙漏模式的扩展，沿钢管的径厚方向划分为4层单元。钢材的本构关系采用理想的弹塑性关系，屈服强度为355 MPa，初始弹性模量为210 GPa。FRP模型采用连续均匀壳单元S4R进行建模，材料本构关系为线弹性，由于碳纤维为正交异性材料，因此材料属性定义为单层板，各项材料参数定义如表4所示，其中E1为CFRP沿纤维方向弹性模量，按表3取值；E2为垂直于纤维方向的弹性模量，由于该方向不考虑纤维强度，因此按表1中基体树脂的弹性模量取值，μ为材料泊松比，G12，G13，G23分别为材料各平面内剪切模量，本文试验未对此项参数进行试验，故参考相关文献[9]进行设置，结果表明该项参数对计算结果影响很小，因此将三者按相等取值。

表4CFRP材料参数Tab.4Material Parameters of CFRP

为模拟真实的试验条件，模型边界条件设置为固定端限制3个位移方向，加载端加载位移方向释放，固定其余位移方向，模型两端转角均不作限制。同时为保证计算结果的收敛性和精确性，在变形较大和较早进入塑性的跨中截面附近以及受力较为复杂的加载端部进行网格细分。另外为了便于偏心加载，在轴压构件两端建立解析刚体壳作为加载载体，解析刚体与钢管之间采用Tie连接。有限元模型如图7所示。

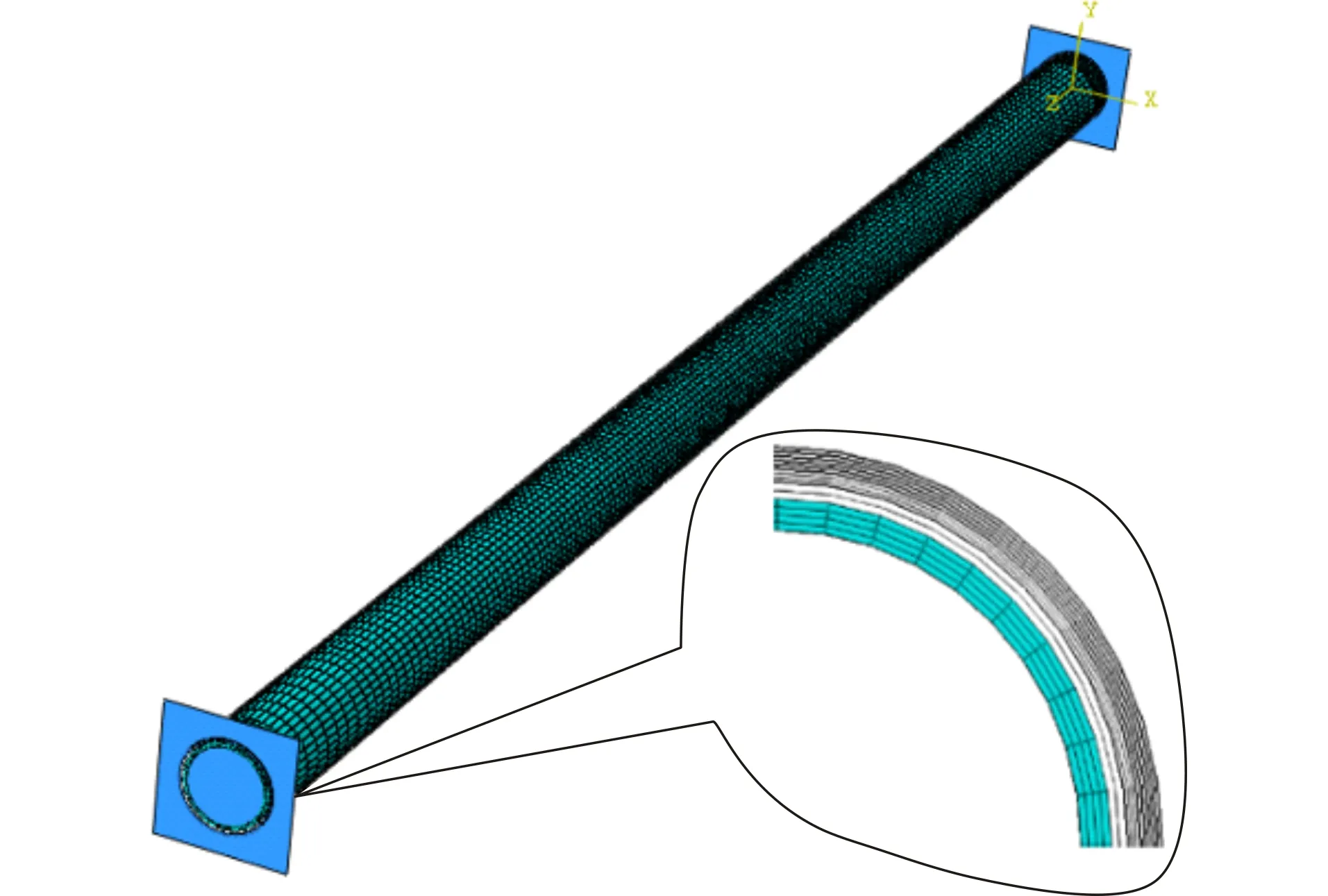
图7有限元模型Fig.7Finite Element Model

由于在轴压构件达到稳定承载力之前，各截面满足平截面假定，因此各层纤维及纤维与钢管之间的接触类型设置为Tie连接。本文研究构件为轴压长柱，无须做线性摄动屈曲分析即可判断其失稳模态，因此本文采用设置加载初偏心的方式来考虑试验构件的初始缺陷，偏心距选取表3中未加固钢管承载力进行确定。根据试验条件进行位移加载，采用基于弧长法的Static，Riks求解器进行求解。

3.2 有限元计算结果

根据ABAQUS计算结果，绘制了构件处于稳定承载力时CFRP沿构件全长的纵向应力云图。由于模型应力分布对称，本文仅给出模型跨中截面以下部分，如图8所示。通过纵向应力云图可以看出，轴压构件在其达到稳定承载力时，CFRP沿构件全长纵向均受压，进一步验证了加固构件稳定承载力的提高源于CFRP的抗压贡献。

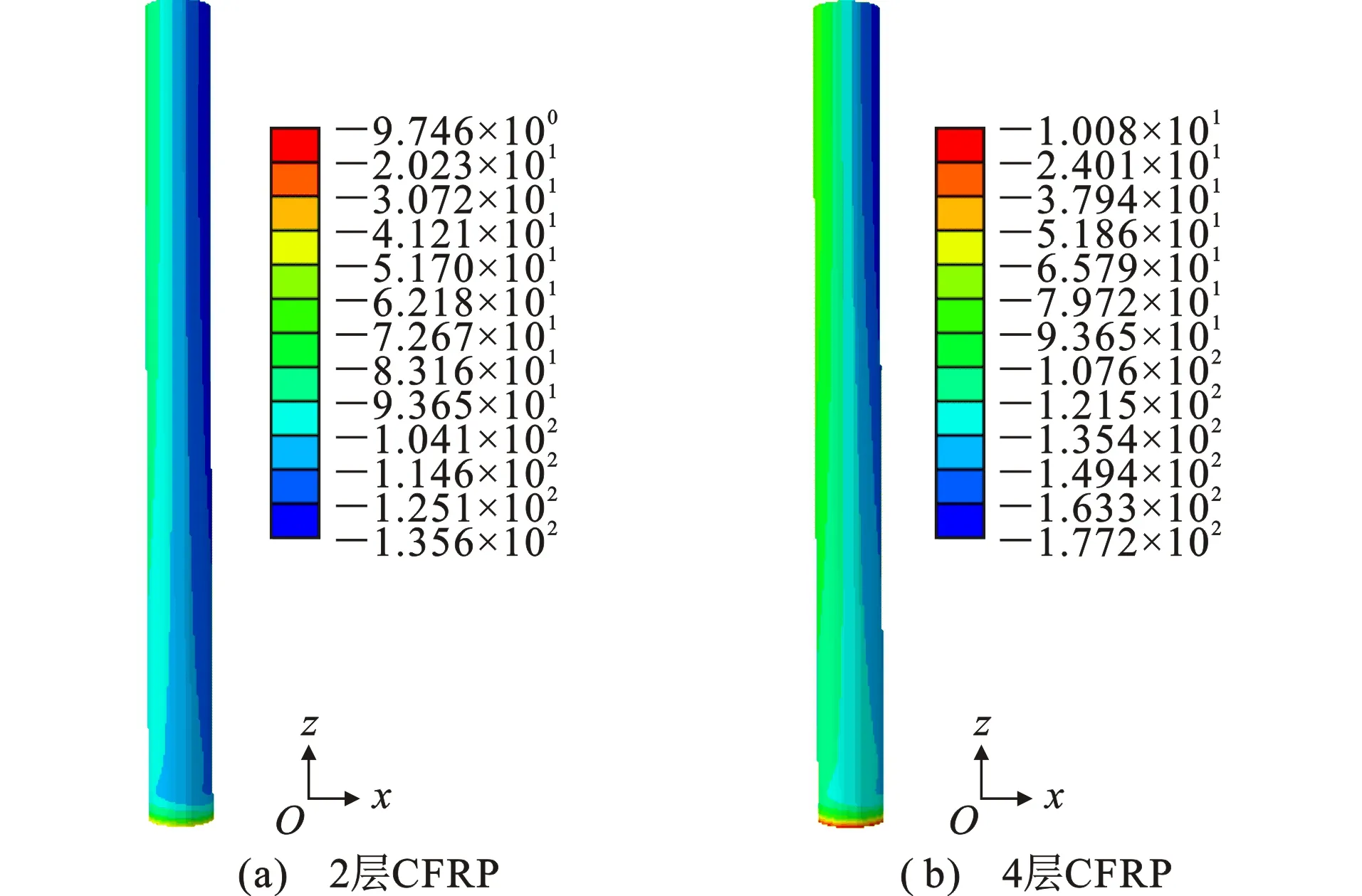
图8CFRP纵向应力云图(单位:MPa)Fig.8CFRP Longitudinal Stress Nephograms (Unit:MPa)

将ABAQUS计算结果与纤维模型计算结果进行对比，得到如图9所示的荷载-位移曲线。由图9可以看出，2种数值计算方法所得到的结果吻合较好，从而可以验证纤维模型计算过程的正确性。

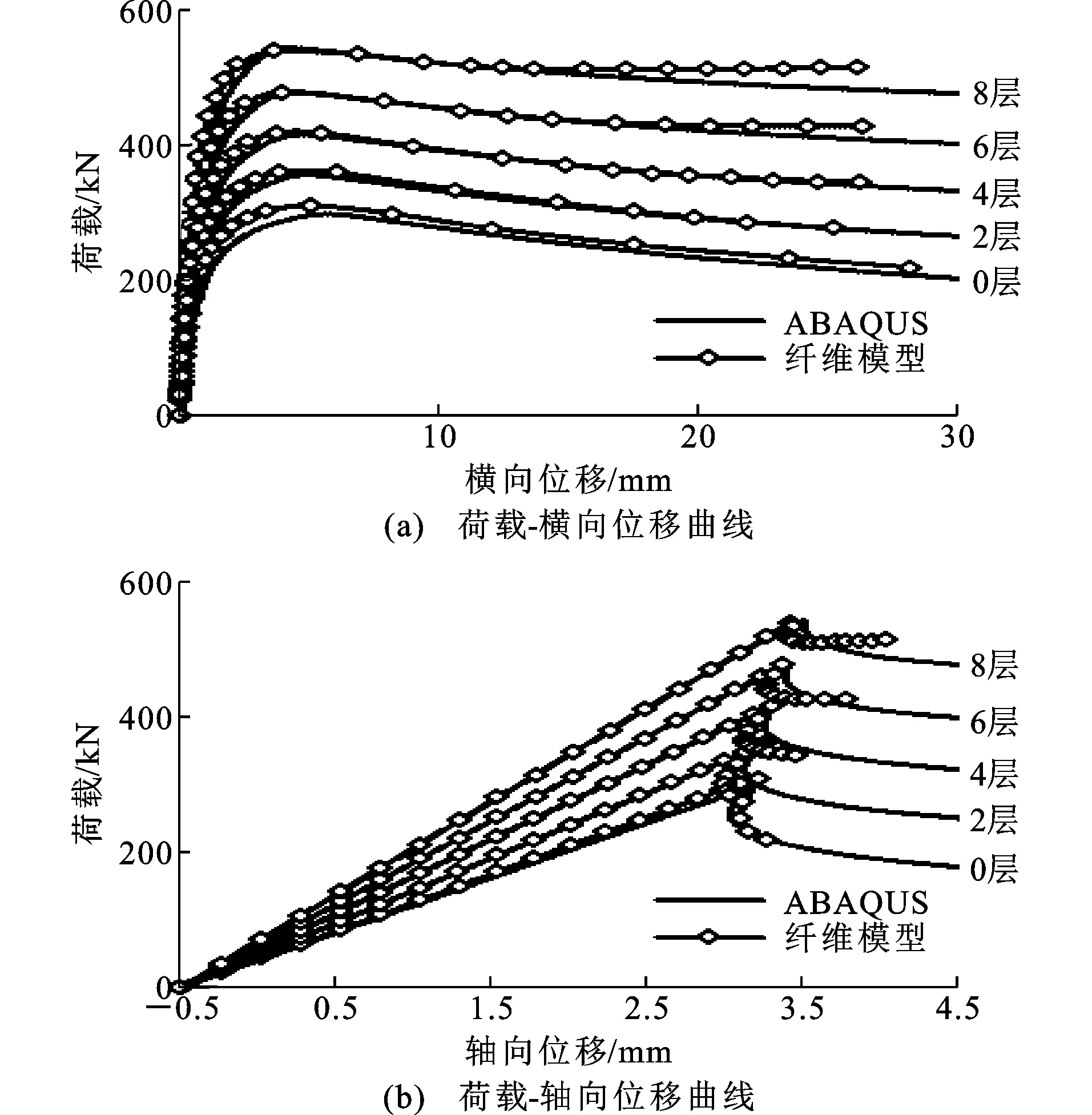
图9ABAQUS与纤维模型荷载-位移曲线Fig.9Load-displacement Curves in ABAQUS and Fiber Element Model

同时，本文将有限元计算结果与试验结果进行对比，得到轴压构件荷载-横向位移曲线，如图10所示。由图10可以看出，ABAQUS与试验得到的加固构件承载力误差在允许范围内，说明依靠纤维模型分析得到的CFRP抗压弹性模量是合理的。

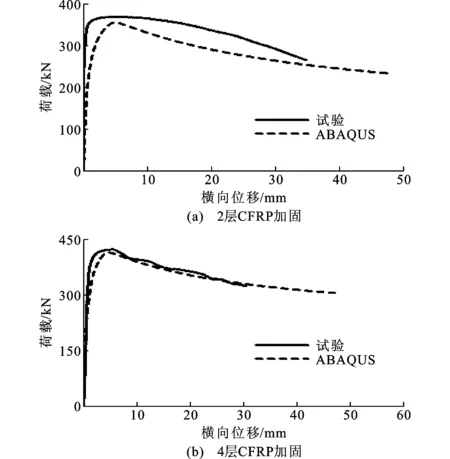
图10ABAQUS与试验荷载-横向位移曲线Fig.10Load-lateral Displacement Curves in ABAQUS and Test

4 CFRP加固效率

本文提出的轴压构件稳定承载力数值分析方法的前提是加固构件外层纤维仅承受压力，即需满足轴压构件在达到其稳定承载力之前为全截面受压状态。截面的受力状态与加载偏心距有关，随着加载偏心距的增大，跨中截面外侧将提前进入受拉区，无法满足数值模型的计算条件。本文通过纤维模型法计算了加固构件达到极限承载力时构件中点截面受压纤维面积，并提出纤维加固效率的概念，以表示CFRP的抗压贡献效率，即

(8)

式中：ρc为CFRP加固效率；Ac为中点截面受压纤维面积；Af为中点截面纤维总面积。

CFRP的受力状态与加载偏心距有关，随着加载偏心距的增大，中点截面外侧将会提前承受拉力，为了研究纤维受压率随偏心距的变化规律，本文利用纤维模型分别计算了不同的加载偏心距构件在达到极限承载力时中点截面纤维受压率，并绘出如图11所示关系曲线。

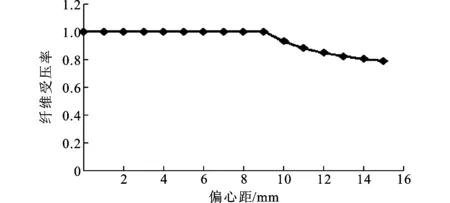
图11纤维受压率与偏心距关系曲线Fig.11Relation of Fiber Compression Ratio and Eccentricity

由图11可以看出，加载偏心距在达到9 mm以后，截面纤维受压率开始逐渐降低，说明部分纤维对承载力的贡献未得到充分利用，偏心距越大，这种现象越明显。据此可以得出结论：随着加载偏心距的增大，CFRP对长轴压构件承载力的贡献效率逐渐降低，因此对于此类加固构件的使用应该尽量减小加载偏心距，以充分利用CFRP的抗压强度。

对于一般的轴心受压构件，加载偏心距主要由轴压构件的初始缺陷引起，各国钢结构设计规范一般均要求由构件的初始缺陷引起的初始偏心距小于L/1 000[21]。从本文分析来看，在初始偏心距小于L/1 000的情况下，轴压构件满足其稳定承载力之前的全截面受压要求。因此，本文所提出的CFRP加固圆形钢管轴压承载力分析方法可以作为此类构件研究的一种简化方法。