超高强钢筋ECC梁受弯性能试验及承载力分析
2021-01-16章一萍李碧雄唐丽娜
章一萍,李碧雄,廖 桥,周 练,唐丽娜
(1. 四川省建筑设计研究院有限公司,四川 成都 610000; 2. 四川大学 深地科学与工程教育部重点实验室, 四川 成都 610065; 3. 同济大学 土木工程学院,上海 200092)
0 引 言
为减少钢筋用量以达到节约资源和保护环境的目的,住房和城乡建设部在《混凝土结构设计规范》(GB 50010—2010)中增加了HRB500和HRBF500级钢筋,但是配置HRB500和HRBF500级钢筋混凝土梁的控裂能力通常较差[1-2]。对此,有学者提出通过增大保护层厚度来提高梁的控裂能力[3],然而试验结果表明,这种方法还存在一些问题。工程用水泥基复合材料(Engineered Cementitious Composites,ECC)作为一种高延性和高韧性的纤维增强水泥基复合材料,其控裂能力、受拉变形能力和受压变形能力都很强。在单轴受拉试验中,ECC表现出多缝开裂和应变硬化的特点,单轴受拉极限应变大于2%[4]。在单轴受压试验中,ECC的峰值压应变可达0.4%~0.5%[5]。尽管ECC的制备成本通常是普通混凝土的数倍,但是根据ECC材料设计理论适当调整ECC中的组分可大幅降低成本[6-8]。
ECC和钢筋的协调变形能力很强[9-10]。此外,Li等[11]对采用HRB335级钢筋增强的ECC梁进行受弯试验研究,发现该类梁的控裂能力和延性性能均较好。薛会青等[12]以HRB500级钢筋和ECC分别作为梁的纵向受拉钢筋和基体材料,发现受弯屈服时梁的裂缝宽度均在0.09 mm以内,远小于规范对梁裂缝宽度的限值。Noushini等[13]将屈服强度为590 MPa的钢筋与ECC组合成梁,发现梁受弯时表现出较强的延性性能。为减小钢筋用量及增强梁的控裂能力和延性性能,基于前述的研究结果[4-5,9-13],文献[14]提出以超高强钢筋(屈服强度标准值大于等于500 MPa的钢筋)和ECC分别为纵向受拉钢筋和基体材料的超高强钢筋ECC梁(Ultra High Strength Rebar Reinforced Engineered Cementitious Composites Beams, UHSRRE梁),并建立了该类梁的正截面受弯计算理论。
为进一步研究UHSRRE梁的受弯性能,以便为该类梁的工程应用提供相应指导。本文对3根UHSRRE梁、1根普通强度钢筋增强ECC梁(Reinforced Engineered Cementitious Composites Beams,RECC梁)和1根普通强度钢筋增强混凝土梁(Reinforced Concrete Beams,RC梁)进行弯曲试验,分析弯曲试验现象、ECC应变、延性性能和特征弯矩,并研究纵筋配筋率对UHSRRE梁承载力的影响。
1 试验概况
1.1 试件制备
试验采用的ECC中水泥、粉煤灰、水、细骨料、纤维、高效减水剂配合比为62.48∶137.72∶56.78∶137.72∶5.11∶1。水泥为普通硅酸盐水泥P.O 42.5R,粉煤灰为F类Ⅰ级粉煤灰,细骨料为70~120目的石英砂,减水剂为聚羧酸高效减水剂(砂浆减水率Rm≥23%)。纤维采用聚乙烯醇纤维(Polyvinyl Alcohol Fiber,PVA纤维),纤维性能见表1。混凝土中水泥、水、细骨料、粗骨料、高效减水剂配合比为200∶61.96∶253.62∶365.22∶1。细骨料采用河砂(属于细砂),粗骨料为粒径5~15 mm的碎石,水泥和减水剂同前。试件主要参数如表2所示,尺寸和配筋见图1,其中F为荷载。

表1PVA纤维性能Tab.1Properties of PVA Fiber

表2试件主要参数Tab.2Main Parameters of Specimens
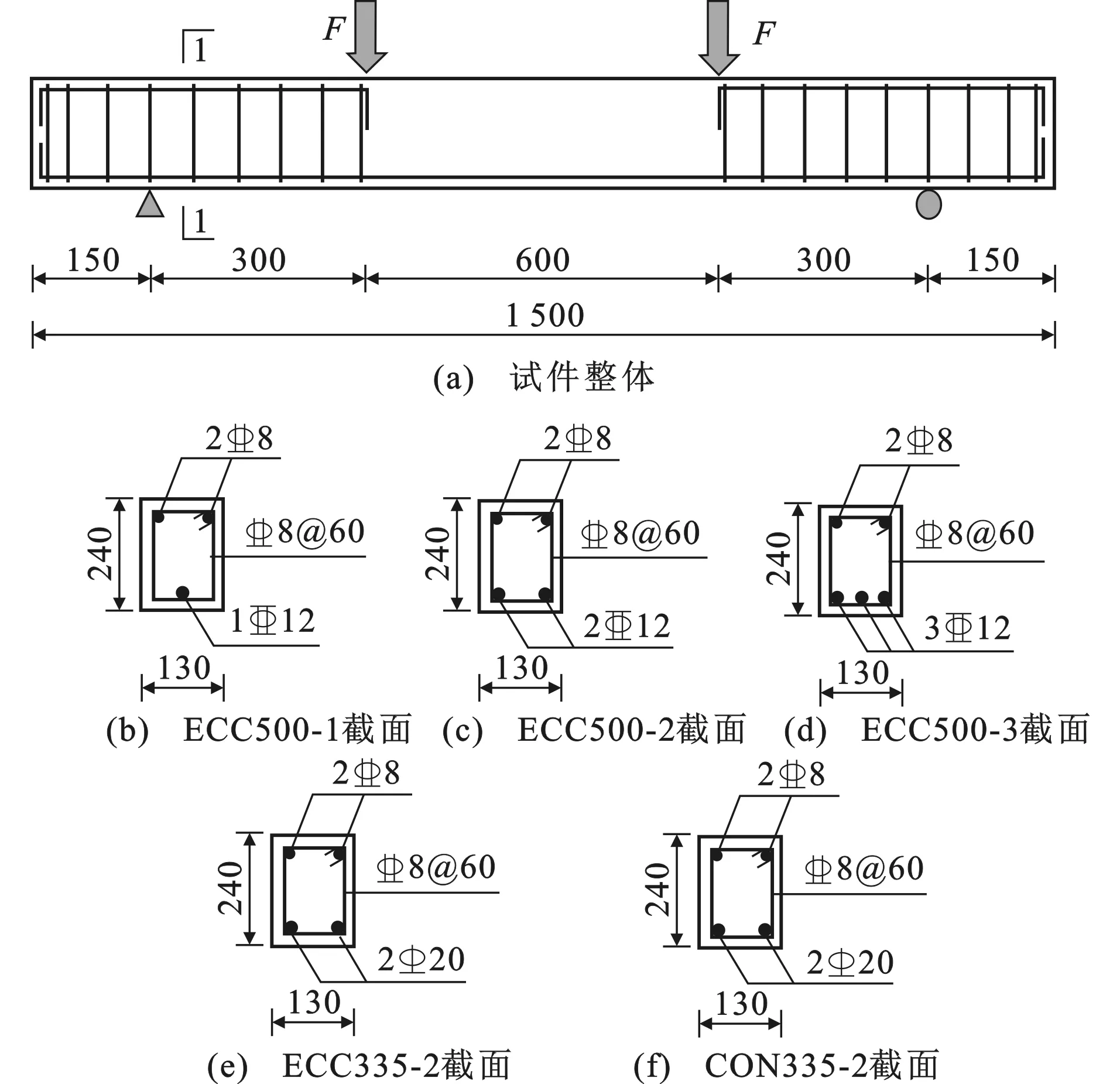
图1试件的尺寸和配筋(单位:mm)Fig.1Dimension and Reinforcement of Specimens (Unit:mm)
在制备UHSRRE梁和RECC梁的过程中采用振捣棒振捣密实ECC。在温度约为10 ℃的室内环境中洒水养护梁7 d后拆模,接着便以每天洒水2次的养护方式再养护梁21 d。为防止水分蒸发,需使用薄膜覆盖梁。浇筑梁的同时,制作3个边长为100 mm的ECC或混凝土立方体及3个尺寸为300 mm×50 mm×20 mm的ECC薄板,立方体和薄板的养护制度与梁的相同。
1.2 材料性能
ECC和混凝土的单轴受压峰值强度分别为26.5 MPa和66.83 MPa,后者约为前者的2.5倍。这是因为养护时间短及养护的温度和湿度低,使得ECC中的粉煤灰发生二次水化反应偏难,粉煤灰在早龄期主要充当惰性填充料[15]。另一方面,ECC中的胶凝材料主要为粉煤灰,水泥质量仅为粉煤灰的45%左右。通过应变片测得ECC的单轴受压峰值应变为0.36%。
经三点弯曲试验测得ECC薄板的荷载-跨中挠度曲线,如图2所示。开裂前,荷载与跨中挠度呈正比关系,ECC处于弹性受力阶段。随跨中挠度的增加,ECC进入稳态开裂阶段,曲线呈“锯齿”状,挠度硬化明显。值得注意的是,荷载-跨中挠度曲线每波动一次基本对应着新裂缝产生或旧裂缝扩展。在试验结束后卸载时,可明显观测到ECC薄板发生弹性恢复变形。ECC薄板受拉面的裂缝分布见图2,所有裂缝均分布在薄板跨中附近,ECC多缝开裂的特点明显,缝宽均小于100 μm(不包含主裂缝),ECC控裂能力突出。为便于确定ECC单轴受拉极限应变,密歇根大学的Qian等[16]建议通过ECC的弯曲试验结果来计算得到单轴受拉极限应变。本文采用与此类似的方法(文献[17]建议的公式)来确定ECC的单轴受拉极限应变,算得ECC单轴受拉极限应变为2.61%。
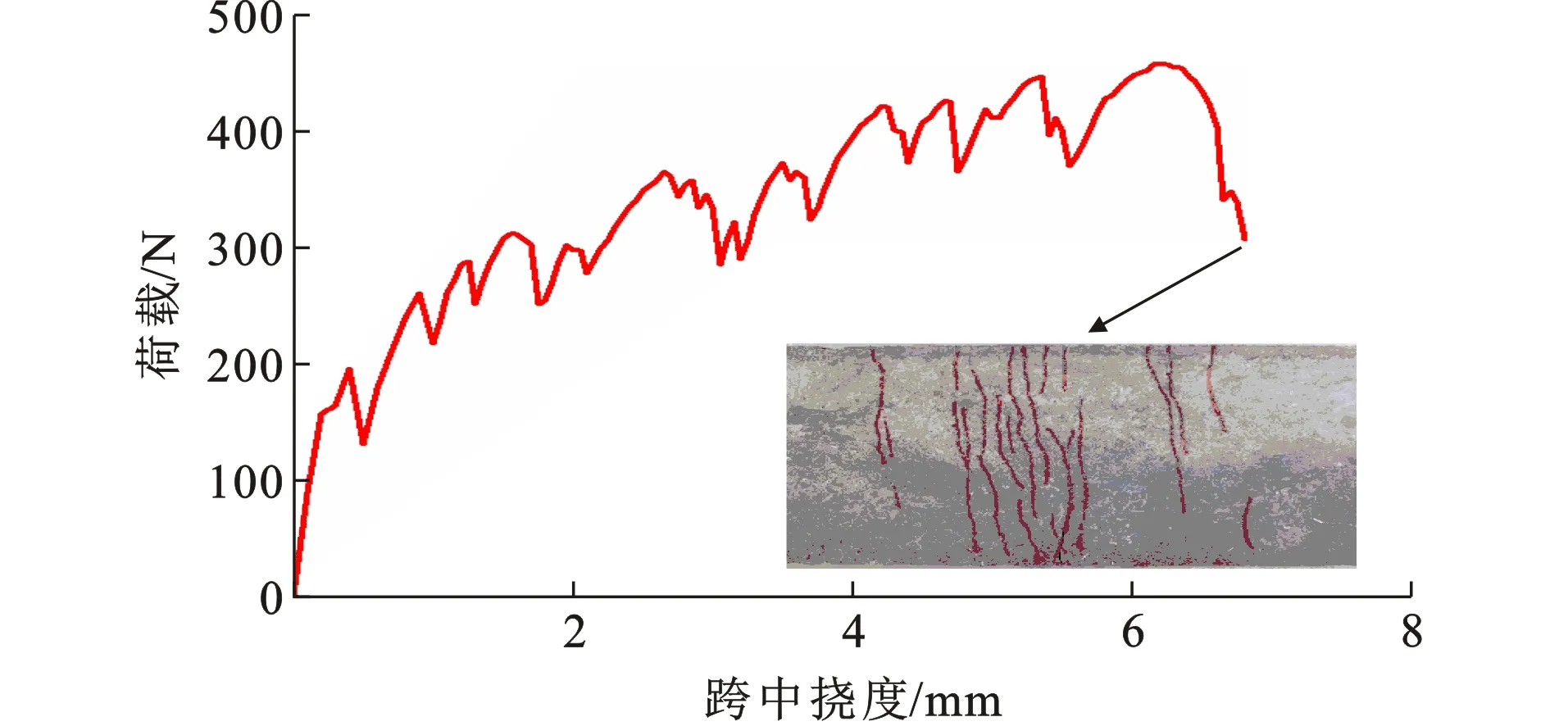
图2ECC薄板的荷载-跨中挠度曲线及裂缝分布Fig.2Load-midspan Deflection Curve and Crack Pattern of ECC Sheet
钢筋力学性能见表3。由于HRB500级钢筋强度最大,所以断后伸长率最小,受拉变形能力最弱。
1.3 试验方案
在梁的侧面设置6个80 mm×2.5 mm的应变片,顶面布设3个80 mm×2.5 mm的应变片,底面设置5个50 mm×3 mm的应变片。在纵向受拉钢筋表面设置4个5 mm×3 mm的应变片。应当指出的是,以上应变片均被布置在梁的纯弯段内。为测定梁的跨中挠度,在支座和跨中分别设置数显千分表。试验过程中,采用HC-CK101裂缝宽度观测仪读取裂缝宽度。

表3钢筋的力学性能Tab.3Mechanical Properties of Steel Bars
加载示意图如图3所示,通过微机控制电液伺服万能试验机对表2中5根梁分别进行弯曲试验。对试件CON335-2采用分级加载,每级荷载约为试验梁预估极限荷载的5%。对余下4根梁采用荷载-位移混合控制加载,即在梁的纵向受拉钢筋开始屈服前,以每级荷载约为试验梁预估极限荷载的5%进行分级加载,之后采用位移控制加载,其速率为0.25 mm·min-1。
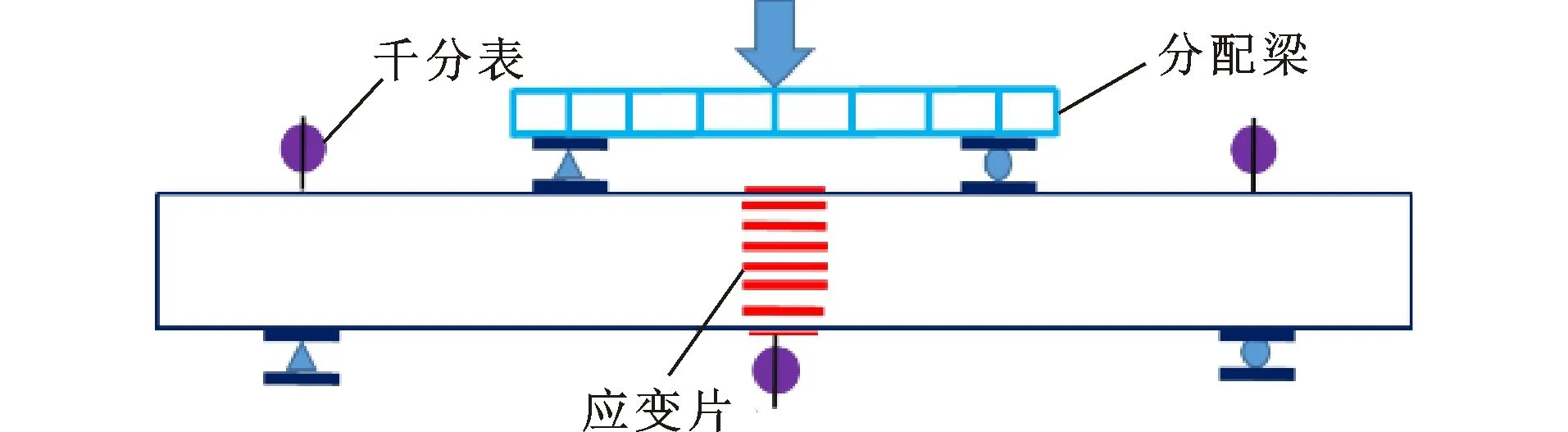
图3加载示意图Fig.3Loading Diagram
2 试验结果及分析
2.1 试验现象
5根梁均发生的是弯曲破坏,其典型破坏形态见图4。UHSRRE梁和RECC梁的纵向受拉钢筋首先屈服,之后梁受压区边缘ECC的应变大于ECC单轴受压峰值应变,梁顶面出现压缩“褶皱”。另一方面,同RC梁相比,UHSRRE梁和RECC梁的控裂能力很强。当RC梁发生破坏时,其纯弯段的裂缝数量仅为6条,并且每条裂缝的宽度都大于0.2 mm。当UHSRRE梁和RECC梁出现破坏时,纯弯段的裂缝数量在40条以上,平均裂缝宽度小于0.2 mm。分析认为,由于PVA纤维的有效桥接作用,ECC具有突出的控裂能力,在单轴受拉条件下ECC的裂缝宽度约为60 μm[18],这使得大裂缝可被细化成微细裂缝。另一方面,ECC和钢筋的协调变形能力很强[9-10],裂缝处的钢筋能有效地发挥作用。与RECC梁相比,尽管UHSRRE梁受弯破坏时的平均裂缝宽度略大,但UHSRRE梁的裂缝数量更多。以上表明,UHSRRE梁并未因采用超高强钢筋而使构件的控裂能力明显降低。

图4梁的典型破坏形态Fig.4Typical Failure Modes of Beams
2.2 ECC应变
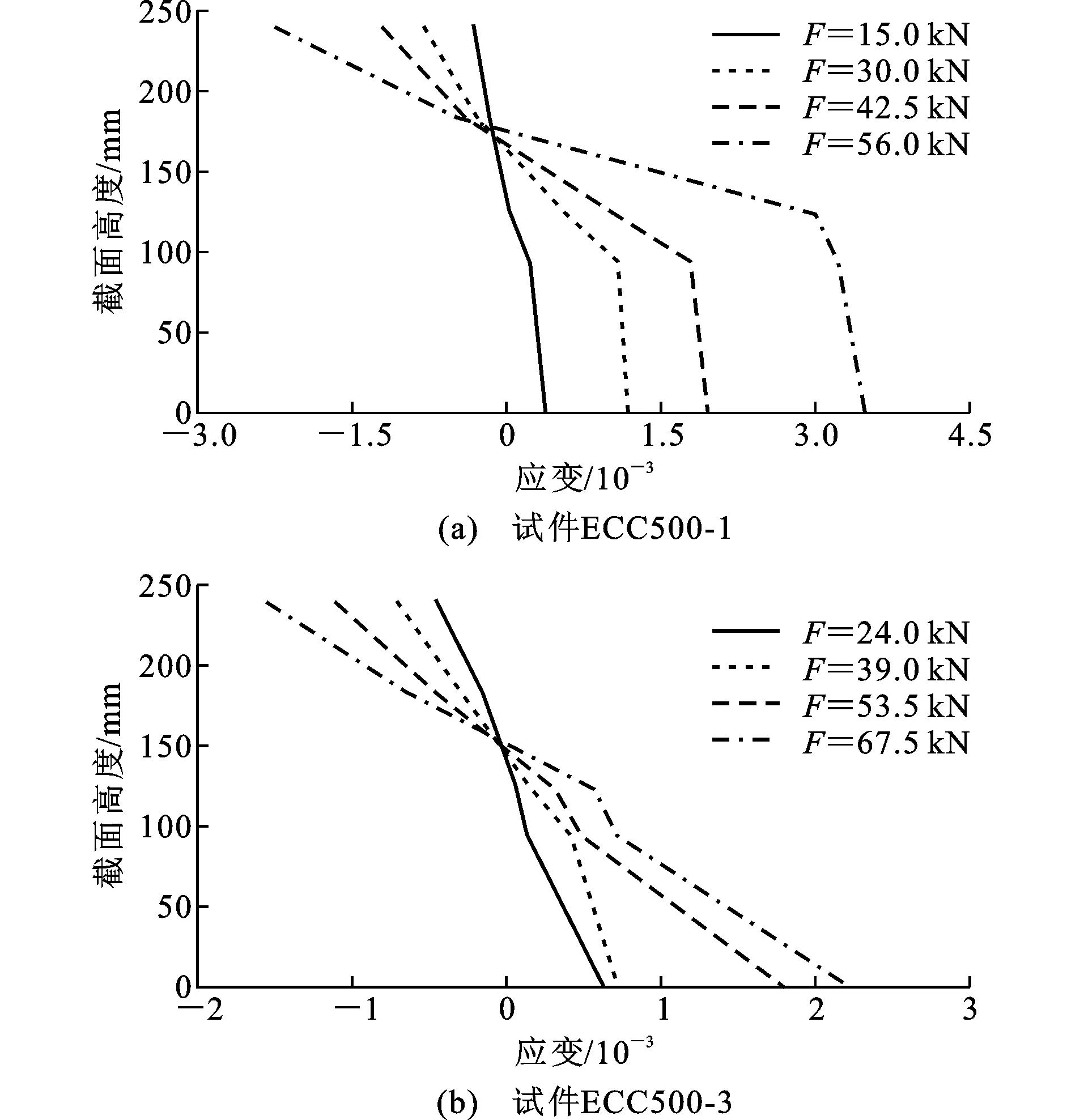
图5不同截面高度处ECC的应变Fig.5ECC Strains at Different Section Heights
图5为UHSRRE梁不同截面高度处ECC的应变。随着荷载增加,UHSRRE梁截面的应变相应增大,截面应变和高度也基本呈线性关系,所以UHSRRE梁截面应变基本符合平均应变的平截面假定。此外,图5表明,随着纵筋配筋率的提高,UHSRRE梁的受压区高度增加。
UHSRRE梁和RECC梁受压区边缘ECC的应变-跨中挠度的关系见图6。当跨中挠度小于4 mm时,ECC应变与跨中挠度呈线性关系,并且4根梁的应变-跨中挠度曲线基本重合。当跨中挠度大于4 mm后,ECC应变与跨中挠度呈非线性关系。由UHSRRE梁的截面应力分布图[14]可知,受压区ECC合力需与纵筋和受拉区ECC的合力平衡。因此,随着纵筋配筋率的提高,梁受压区高度增加(图5),受压区边缘ECC的应变增大。UHSRRE梁和RECC梁受压区边缘的应变峰值均明显大于ECC的单轴受压峰值应变,并且在受压区边缘ECC的应变超过单轴受压峰值应变后,UHSRRE梁所承受的荷载无明显降低。试验中发现,ECC应变达到峰值后便开始降低,这是因为试验加载后期梁顶面有压缩“褶皱”,使得应变片向平面外凸起,导致应变片出现受拉变形。
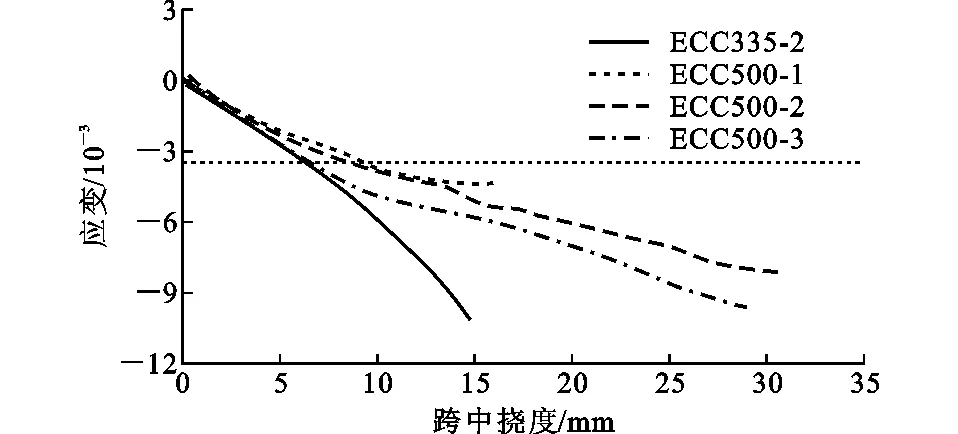
图6梁受压区边缘ECC的应变-跨中挠度关系Fig.6Relationship Between ECC Strains and Midspan Deflection at Edge of Compression Zone of Beams
图7为UHSRRE梁和RECC梁弯曲试验过程中所测得的梁受拉区边缘ECC拉应变最大值。RECC梁受拉区边缘ECC拉应变最大值小于ECC单轴受拉极限应变,表明RECC梁受拉区的ECC不退出工作。这与文献[19]在建立RUHTCC梁受弯计算理论时认为受拉区ECC不退出工作的假定吻合。UHSRRE梁受拉区边缘ECC拉应变最大值也小于ECC单轴受拉极限应变,即UHSRRE梁的受拉区ECC也不退出工作。根据UHSRRE梁的截面应力分布图[14]可知,纵筋和受拉区ECC的合力需与受压区ECC合力平衡,纵筋配筋率的提高将使受压区ECC合力增加,受压区ECC应变相应变大,从而使受拉区ECC应变也增加。因此,随着纵筋配筋率的提高,UHSRRE梁受拉区边缘ECC拉应变最大值增加,ECC优异的受拉变形能力得到进一步发挥。
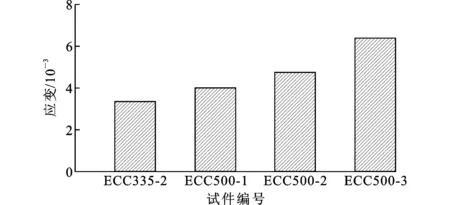
图7梁受拉区边缘ECC拉应变最大值Fig.7Maximum Tensile Strains of ECC at Edge of Tensile Zone of Beams
2.3 延性性能
衡量受弯构件延性性能的指标有很多种,如能量延性系数和位移(或曲率)延性系数。能量延性系数不但能反映构件的变形储备,而且可反映其承载力储备[20]。此外,试验梁的纵筋配筋率变化范围较大(0.42%~2.39 %),各梁之间的承载力存在明显差异(表4),所以采用能量延性系数μ来评价梁的延性性能。能量延性系数计算式为
μ=Eu/Ey
(1)
式中:Ey为受弯构件屈服时的变形能;Eu为极限变形能。
UHSRRE梁和RECC梁的能量延性系数如表4所示。随着纵筋配筋率的增加,UHSRRE梁的能量延性系数先增后减。虽然UHSRRE梁的承载力随着配筋率的提高而增加,但梁的变形能力下降。因此,UHSRRE梁的能量延性系数随着配筋率的增加最后出现减小。与RECC梁相比,试件ECC500-2的能量延性系数提高了25.71 %,表明当UHSRRE梁具有适当的纵筋配筋率时,其延性性能将优于RECC梁的延性性能。
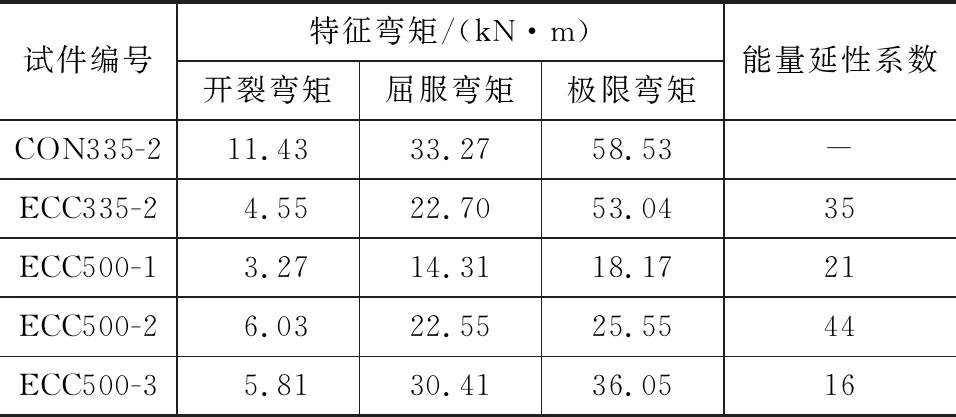
表4梁的受弯试验结果Tab.4Flexure Test Results of Beams
2.4 特征弯矩
5根梁的特征弯矩见表4。由于RC梁的纵筋配筋率和混凝土的单轴受压峰值强度均很高,加之试验采用的HRB335级钢筋的极限强度约为其屈服强度的2倍,故试件CON335-2的特征弯矩最大,且屈服后其抗弯承载力尚有明显的提高。与此相反的是,试件ECC500-1的配筋率最低,ECC单轴受压峰值强度也偏低,所以该试件的特征弯矩最小。随着配筋率的增加,UHSRRE梁的特征弯矩(除开裂弯矩)增大。值得注意的是,尽管混凝土的单轴受压峰值强度是ECC的2.5倍,但RC梁和RECC梁的极限弯矩非常接近,后者约为前者的0.91倍,这是因为RECC梁受拉区边缘ECC拉应变最大值小于ECC单轴受拉极限应变,即梁受拉区的ECC没有退出工作。另一方面,RECC梁受压区ECC塑性变形发展更为充分,受压区高度更大。
3 承载力分析
为对比UHSRRE梁和RC梁的承载力(极限弯矩),取与混凝土单轴受压峰值强度较为相近的ECC作为UHSRRE梁的基体材料。由文献[21]得ECC力学参数:ECC单轴受压刚度变化点对应的强度σcc和应变εcc分别为35.1 MPa和0.073%,单轴受压峰值强度σcp和应变εcp分别为52.6 MPa和0.22%。单轴受拉初裂强度σtc和应变εtc分别为2.2 MPa和0.19%,单轴受拉极限强度σtu和应变εtu分别为6.5 MPa和7.98%。此外,UHSRRE梁截面的高度h和宽度b分别为240 mm和130 mm。UHSRRE梁的纵向受拉钢筋为HRB500E级钢筋或HRB600级钢筋,钢筋直径d、屈服强度σy、屈服应变εy、极限强度σsu和极限强度对应的应变εsu如表5所示[22]。保护层厚度采用20 mm,箍筋和架立钢筋均选用直径为8 mm的HRB400级钢筋。

表5纵筋力学参数Tab.5Mechanical Parameters of Longitudinal Steel Bars
根据UHSRRE梁的受弯计算理论[14]可知
Tc+Ts=Cc
(2)
(3)
(4)
式中:Ts为纵向受拉钢筋合力;Tc为受拉区ECC合力;Cc为受压区ECC合力;a为ECC受拉区开裂高度;ε(h)为h高度处(以受拉区边缘为原点,建立沿截面高度竖直向上的x轴坐标系)ECC的应变;as为下部纵向受拉钢筋合力点到受拉边缘的竖向距离;As,εs为纵筋的面积和应变;xc为受压区高度;e为受压区刚度变化点与受拉区边缘之间的竖向距离;k2=(σtu-σtc)/(εtu-εtc);k4=(σcp-σcc)/(εcp-εcc);k6=(σsu-σy)/(εsu-εy)。
联立式(2)~(4),解出受压区高度xc。根据力矩平衡条件可对UHSRRE梁的受拉区边缘取矩,整理得弯矩M为
(5)
令ε(h)=εcp,可解得xc,代入式(5)中得梁的承载力。
基于上述受弯计算理论,通过MATLAB软件编程计算得到UHSRRE梁的承载力,如表6所示。当纵筋配筋率为2.39%时,尽管混凝土的单轴受压峰值强度为ECC的1.27倍,但以HRB500E为纵向受拉钢筋的UHSRRE梁的承载力仅比RC梁低1.61%;配有HRB600级钢筋的UHSRRE梁的承载力比RC梁提高了9.53%。另一方面,文献[12]的试验结果表明,当纵筋配筋率为1.39%时,UHSRRE梁的承载力比RC梁提高了50.07%;当配筋率为0.70%时,UHSRRE梁的承载力较RC梁提高了85.02%。以上表明,UHSRRE梁可以实现钢筋用量的减少。
4 结语
(1)UHSRRE梁和RECC梁的控裂能力均比RC梁的控裂能力强。与RECC梁相比,UHSRRE梁并未因采用超高强钢筋而使其控裂能力明显下降。
(2)UHSRRE梁截面的应变和高度基本呈线性关系,梁截面应变基本符合平均应变的平截面假定。UHSRRE梁受拉区边缘的ECC应变小于ECC单轴受拉极限应变,UHSRRE梁受拉区的ECC始终不退出工作。
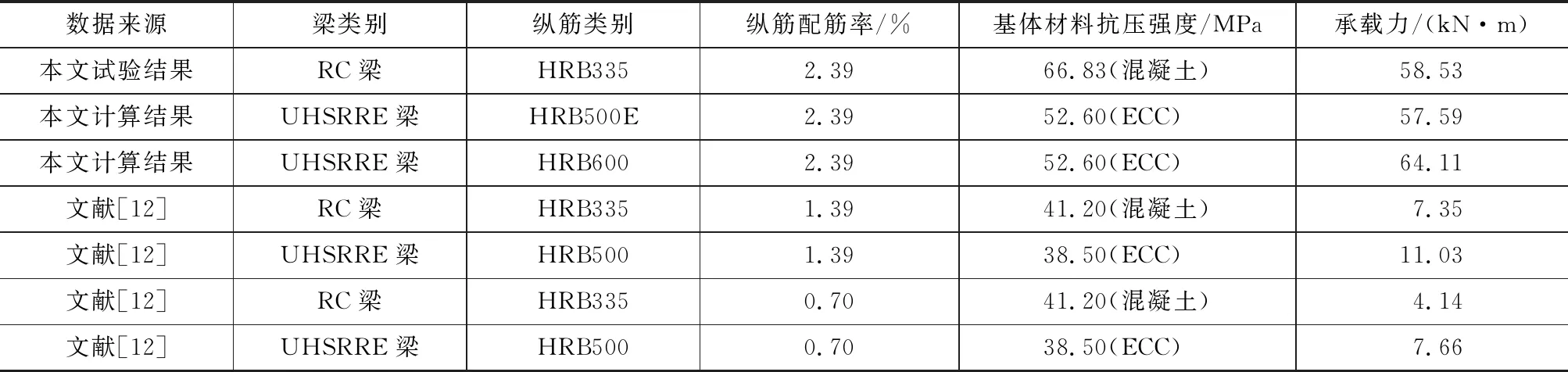
表6UHSRRE梁和RC梁的承载力比较Tab.6Comparison of Bearing Capacity Between UHSRRE Beams and RC Beams
(3)随UHSRRE梁的纵筋配筋率提高,梁受压区边缘ECC压应变和受拉区边缘ECC拉应变的最大值均增加,受压区高度变大,屈服弯矩和承载力增加,但能量延性系数先增后减。当UHSRRE梁具有适当的纵筋配筋率时,其能量延性系数可比RECC梁的大25.71 %。
