角钢混凝土黏结滑移性能试验与数值模拟
2021-01-15赵卫平王振兴董朋昆朱彬荣陈惠玲
赵卫平,王振兴,董朋昆,朱彬荣,陈惠玲
(1.中国矿业大学(北京) 力学与建筑工程学院,北京 100083; 2. 中国电力科学研究院,北京 100192)
0 引 言
型钢混凝土组合结构中钢材与混凝土之间的黏结作用是型钢和混凝土共同工作的基础。研究表明,型钢与混凝土的黏结作用和光圆钢筋与混凝土之间的黏结作用类似,主要由化学胶结力、摩擦阻力和机械咬合力三部分组成[1]。化学胶结力随水泥晶体被剪断或挤碎而丧失,摩擦阻力主要取决于黏结界面上的法向压力和摩擦因数,机械咬合力取决于型钢表面粗糙不平程度[2-5]。型钢和混凝土之间的黏结强度约为光圆钢筋与混凝土之间黏结强度的30%~45%,荷载作用下在型钢和混凝土黏结界面易出现相对滑移[6]。过大的滑移将极大影响型钢与混凝土的共同工作性能,进而影响构件的破坏形态、承载能力、裂缝形成等整体力学行为。
中国学者采用不同的型钢截面形式进行试验研究。郑山锁等[7-8]结合国内外资料研究了工字钢与混凝土的黏结作用,得到影响黏结强度的主要因素有混凝土强度、保护层厚度等。杨勇等[9]对组合H型钢与混凝土的黏结作用进行了推出试验研究,得到的荷载-滑移曲线分为无滑移段、滑移段、破坏段、下降段、残余段5个阶段。李红等[10]进行了T型钢混凝土试件的推出试验,结果表明混凝土强度等级、保护层厚度等对型钢混凝土的黏结强度影响显著。随着输电塔主材结构的发展,内配格构式角钢的钢-混组合构件已展现出施工方便、截面性能优良等特点。王军[11]对内配格构式角钢圆钢管混凝土构件在轴心受拉、偏心受拉、受弯、轴心受压和偏心受压等荷载工况下的极限承载力进行了研究。邓文琴等[12]开展了角钢剪力连接件推出试验研究,钢-混组合试件表现出较好延性。型钢混凝土黏结问题复杂,目前国内外学者主要针对工字钢、H型钢、T型钢与混凝土的黏结问题进行了研究,而对于角钢与混凝土组合结构,主要对抗弯、抗压承载力等力学性能进行研究,对于黏结滑移机理的研究,文献报道较少。
影响黏结性能的因素众多,且黏结界面的内部滑移过程较难直接测定,而有限元分析能够较好弥补宏观试验的不足,在黏结问题的研究中得到了应用。Schneider等[13-15]采用有限元模拟钢管与混凝土界面作用,为钢管混凝土黏结滑移本构关系提供了参考依据,但均未充分考虑钢材与混凝土间的机械咬合力。文献[16]通过面-面接触的接触单元模拟钢筋与混凝土界面的力学行为,该学者通过建立隆起的钢筋肋单元提供机械咬合力,但与型钢混凝土间机械咬合力的产生有所不同。此外,目前采用的有限元模型较少充分考虑滑移面变化对黏结性能的影响,有限元模型仍有优化的空间。
本文根据正交试验原理,以黏结长度、保护层厚度和混凝土强度为敏感参数,设计了9个角钢混凝土推出试件,获得了加载端荷载-位移曲线。利用ANSYS对推出过程进行了精细化有限元数值模拟。
1 试验概况
1.1 试件设计
角钢混凝土试件的尺寸为150 mm×150 mm×150 mm,角钢横截面形心与混凝土形心重合,试件简图见图1(a)。采用正交试验设计方法,研究黏结长度la、保护层厚度C[取角钢边缘距离混凝土外边缘的最短距离,即C=min{C1,C2,C3,C4},保护层厚度见图1(b)]、混凝土强度fc对角钢与混凝土黏结性能的影响。试验中设计三因素三水平,共有9个标准推出试件,设计参数见表1。
1.2 试验材料及性能
角钢采用山东华安铁塔公司生产的Q235B等边角钢,其力学参数见表2。角钢加载端磨平以保证加载时角钢受力均匀,自由端涂刷石蜡以消除端部效应,见图2。混凝土设计强度为C30,C40,C50,混凝土配合比见表3。依照标准试验方法预留测试强度的试件,每种强度混凝土试件预留6个150 mm×150 mm×150 mm立方体试块,28 d强度实测值见表4。
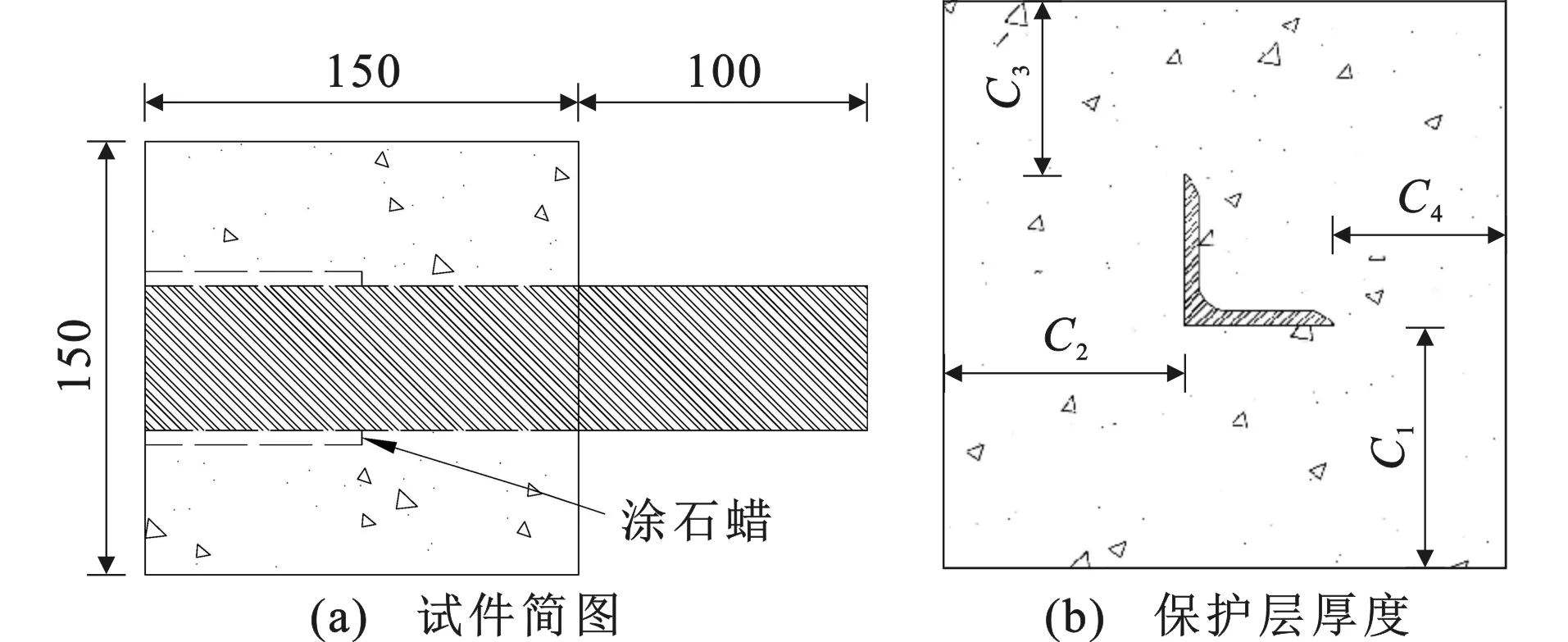
图1试件尺寸(单位:mm)Fig.1Size of Specimens (Unit:mm)
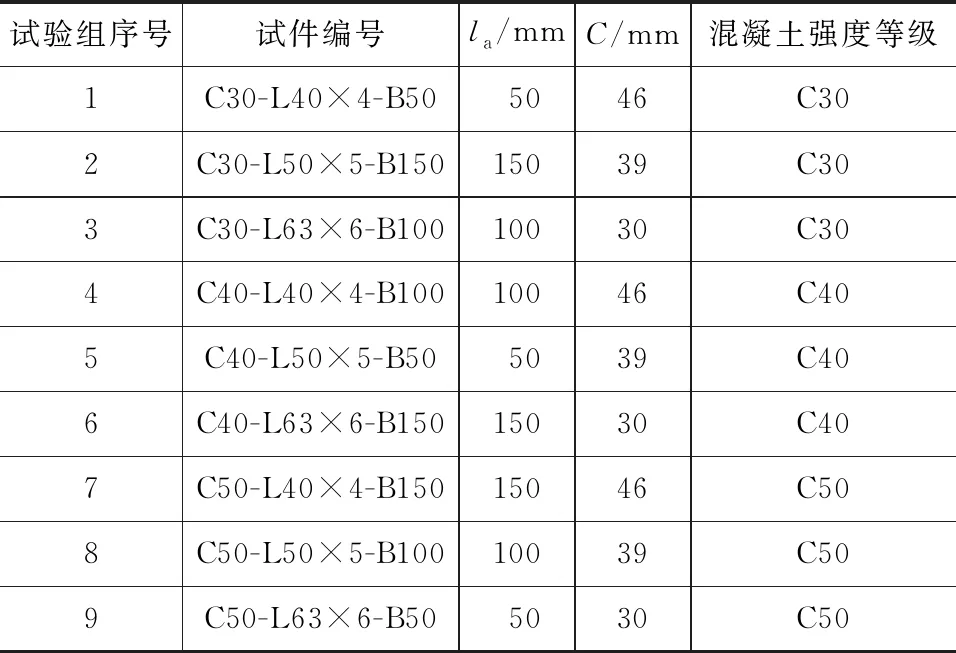
表1试件设计参数Tab.1Design Parameters of Specimens

表2角钢力学参数Tab.2Mechanical Parameters of Angle Steel

图2角钢表面处理Fig.2Angle Steel Surface Preparation
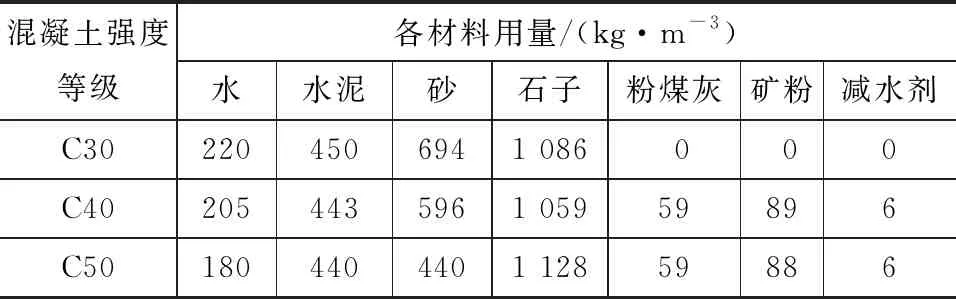
表3混凝土配合比设计Tab.3Proportion Design of Concrete
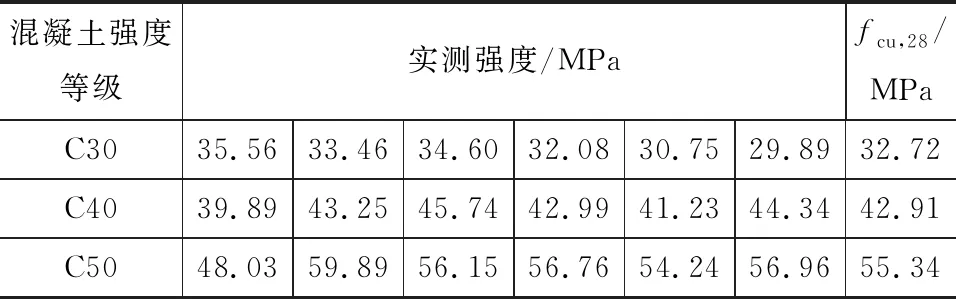
表4混凝土立方体抗压强度Tab.4Measured Concrete Cube Compressive Strength
1.3 加载方案
试验加载采用1 000 kN单轴伺服液压试验机,直接作用于角钢上端,采用位移控制加载方式,保持0.001 mm·s-1的速率,加载端位移达到10 mm时结束加载。在单轴伺服液压试验机加载头两端布置了位移计①,②,支座沉降位移由位移计③,④测得,加载端位移为位移计①,②均值与位移计③,④均值之差。试件下方垫环形钢垫块,为角钢推出预留空间。加载装置和测点布置见图3。
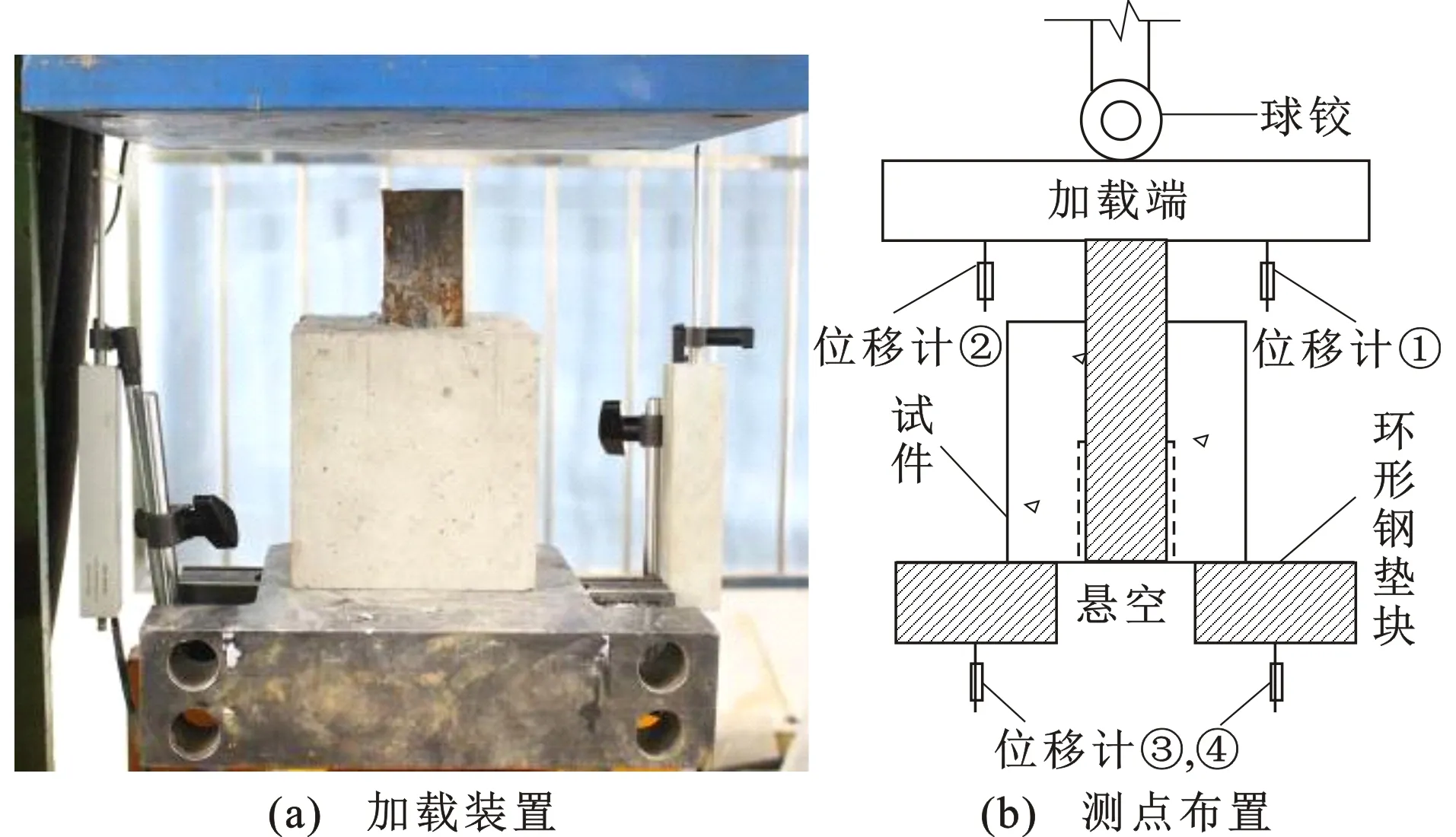
图3加载装置和测点布置Fig.3Loading Device and Test Point Arrangement
2 试验结果与分析
2.1 试验现象与荷载-滑移曲线
试件的破坏分为推出破坏和劈裂破坏2种形态:①推出破坏,角钢推出而混凝土没有发生破坏;②劈裂破坏,角钢推出且沿着角钢纵向的混凝土一侧出现贯通裂缝,裂缝宽度受保护层厚度的影响显著,保护层厚度相对较大(39 mm)时,裂缝较细,保护层厚度相对较小(30 mm)时,裂缝略宽,见图4,混凝土劈裂时,发出较大的“咚”声。

图4劈裂破坏Fig.4Splitting Failure
图5为加载端荷载-滑移曲线(P-S)。由图5可知,相较推出破坏试件,劈裂破坏试件的极限滑移荷载更小,当加载端荷载达到极限滑移荷载后,荷载降低的速率更快,降幅更大。因此发生劈裂破坏后,试件承担荷载的能力极弱甚至完全丧失承载力。
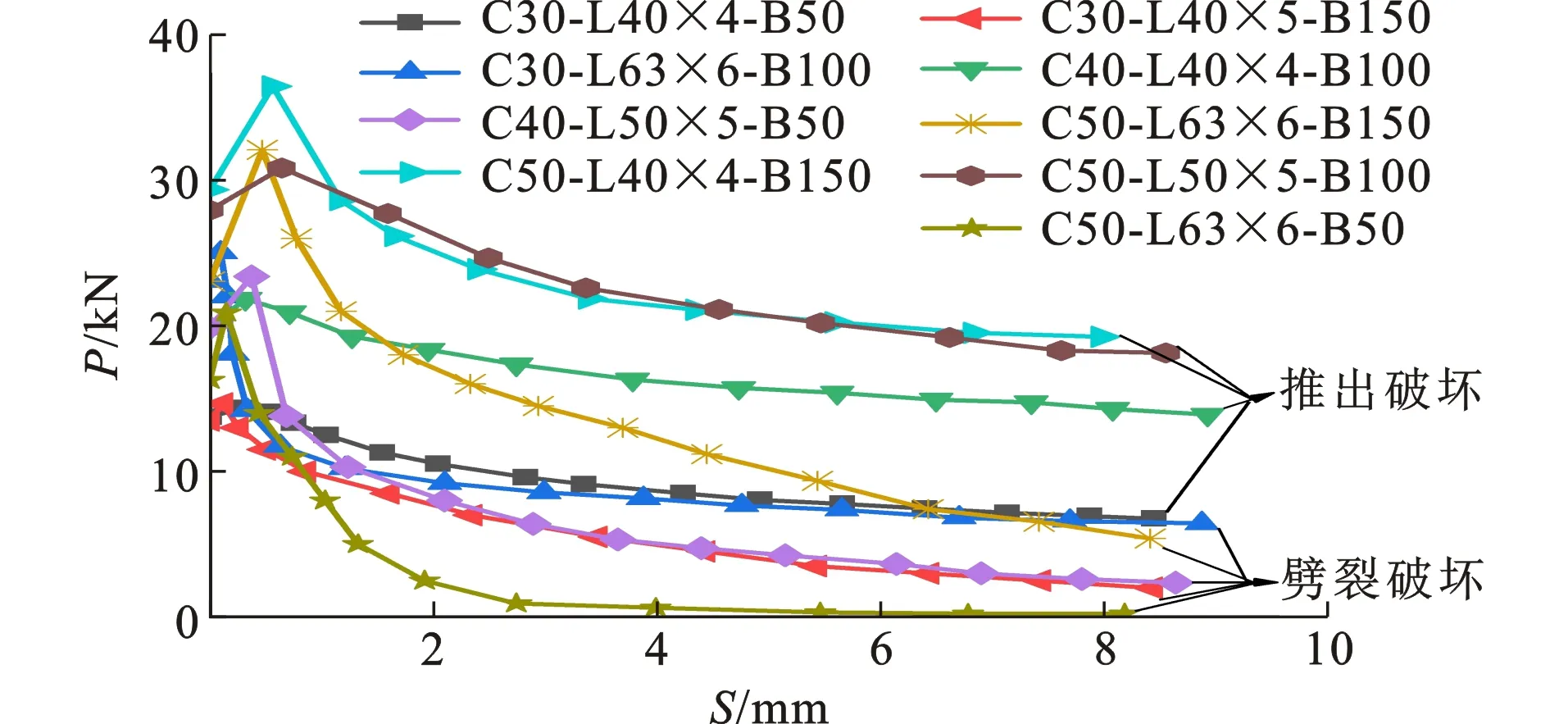
图5加载端荷载-滑移曲线Fig.5Load-slip Curves of Loaded End
2.2 极限黏结强度影响因素分析
在角钢推出过程中,假定沿黏结长度方向各横截面的应力相等,可采用平均黏结强度作为各因素对角钢与混凝土黏结界面影响的分析标准。平均黏结强度τ按照下式计算[17]
(1)
式中:Ca为角钢横截面周长。
黏结滑移特征值见表5。由表5可知,初始滑移荷载与极限滑移荷载比值范围为0.72~0.96,各试件峰值滑移荷载对应的滑移最大值为0.64 mm,即当角钢出现初始滑移荷载后,将会迅速发展为全截面滑移。因此,一旦角钢与混凝土发生滑移,应当给予重视。
本文采用极差分析法[18]研究黏结长度、保护层厚度、混凝土强度在不同正交水平对极限黏结强度的影响。极差分析法采用单一因素下单个水平对应的所有试件黏结强度的均值表示该因素在此水平下
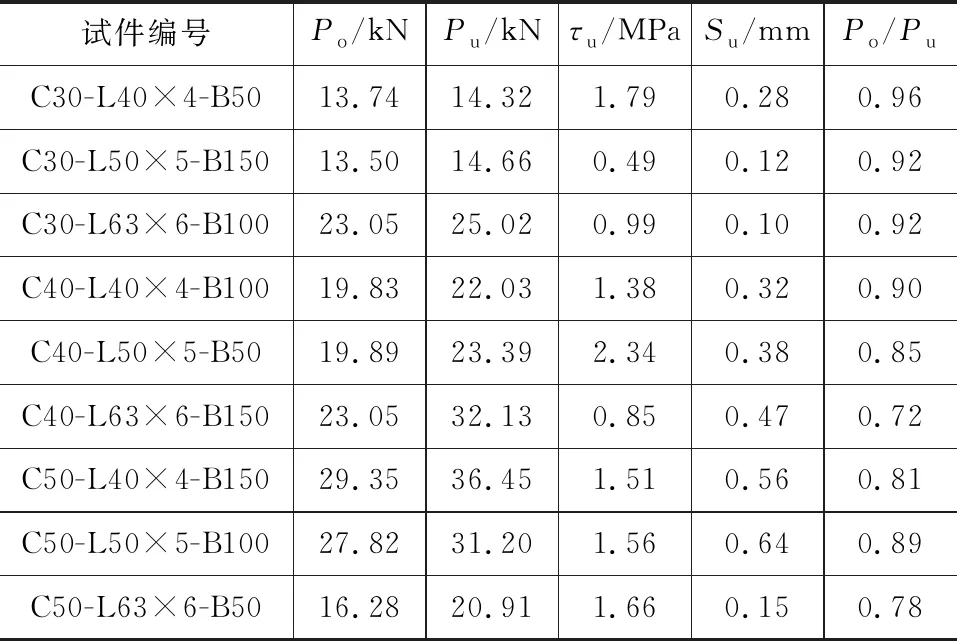
表5黏结滑移特征值Tab.5Eigenvalues of Bond-slip
的黏结强度。取试件C30-L40×4-B50,C40-L50×5-B50,C50-L63×6-B50对应的黏结强度均值来反映界面黏结长度为50 mm对黏结强度的影响。采用极差分析法分析得到各影响因素与极限黏结强度相关关系,如图6所示。由图6中黏结长度与极限黏结强度相关关系可知,在试验黏结长度范围内(50~150 mm),极限黏结强度随黏结长度增大而线性降低。

图6极限黏结强度效应Fig.6Effect of Ultimate Bond Strength
由图6中保护层厚度与极限黏结强度相关关系可知,保护层厚度增加,极限黏结强度显著增大。由于保护层厚度增大能提高混凝土对角钢的侧向约束作用,故极限黏结强度增大[19]。保护层厚度为30~39 mm时,极限黏结强度增加速率远大于保护层厚度为39~46 mm时的增加速率。因此,随着保护层厚度增大,极限黏结强度增加速率降低,但总体极限黏结强度随保护层厚度增大而提高。
由图6中混凝土抗压强度与极限黏结强度相关关系可知,混凝土强度从32.72 MPa增加为42.91 MPa时,极限黏结强度提高约40%,由于混凝土强度增大,增强了混凝土的环箍作用[9],极限黏结强度显著提高。随着混凝土强度由42.91 MPa增大为55.34 MPa时,极限黏结强度仅提高4%。因此当混凝土强度增大至一定值后,极限黏结强度提高不再显著。
2.3 极限黏结强度计算方法
为探求角钢与混凝土界面极限黏结强度计算方法,以试件黏结长度与混凝土高度之比la/h、混凝土强度fcu、保护层厚度与角钢肢长之比C/L为研究参数,对试验结果进行回归分析,建立黏结强度计算公式,如式(2)所示。极限黏结强度计算值与本文实测值对比结果见图7(平均值为1.001 6,标准差为0.214 76,变异系数为0.214 40),计算值与实测值较为接近,整体误差较小。
0.081 3)
(2)
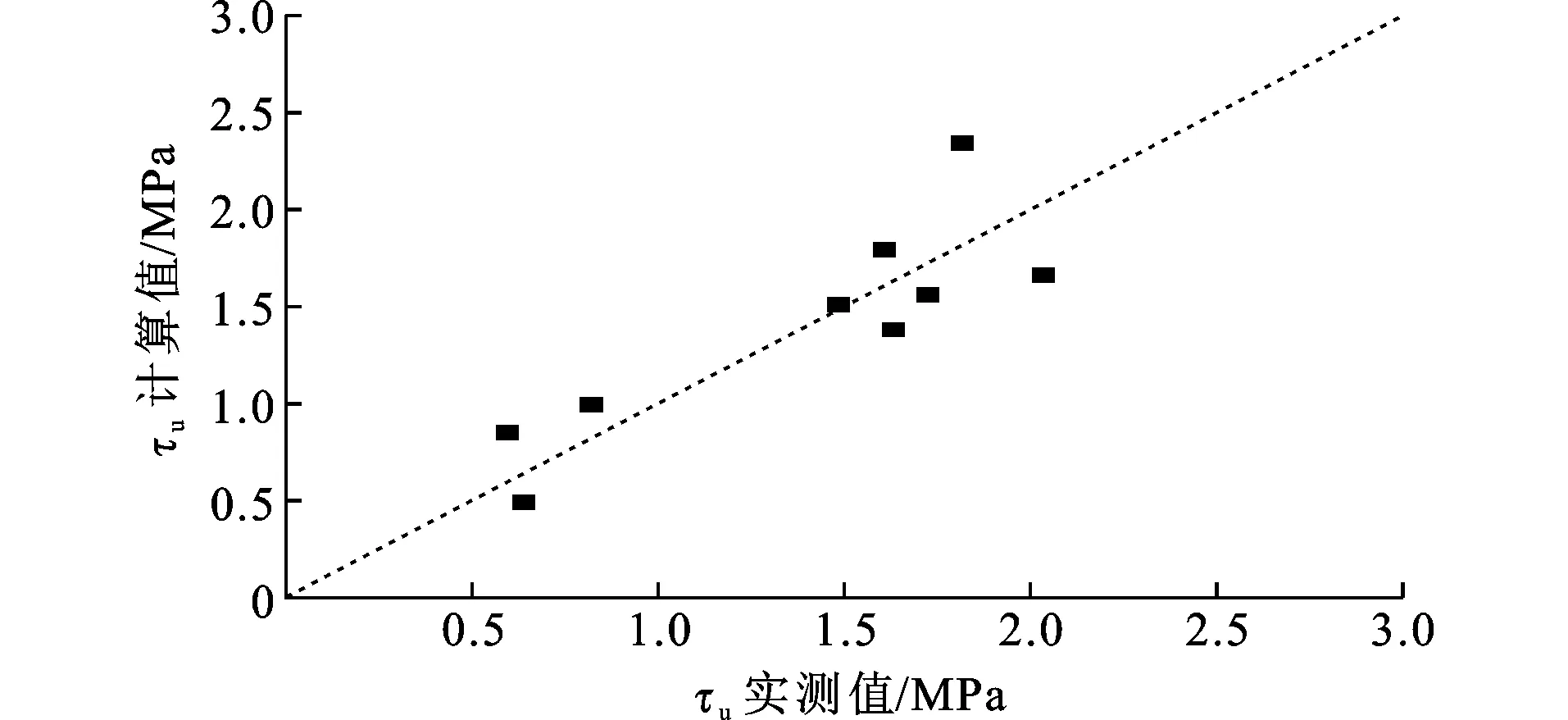
图7极限黏结强度对比Fig.7Comparison of Ultimate Bond Strength
3 有限元分析
3.1 材料本构关系
(1)混凝土:根据《混凝土结构设计规范》[20]标定混凝土单轴受压的应力-应变(σc-εc)关系,如下式所示
(3)
(4)
ε0=0.002+0.5(fck-50)×10-5
(5)
εcu=0.003 3-0.5(fck-50)×10-5
(6)
式中:fck为混凝土28 d抗压强度实测值;n为系数,当n大于2.0时,取2.0;ε0为混凝土压应力为fck时的压应变,当计算的ε0小于0.002时,取0.002;εcu为混凝土极限压应变,当计算的εcu大于0.003 3时,取0.003 3。
混凝土积分点出现裂缝后通过混凝土单轴受拉的应力-应变关系描述。单轴拉力达到抗拉强度后(此时拉应变为εt0),拉应力释放到0.6倍抗拉强度fct。当拉应变达到6εt0时,拉应力降为0。混凝土抗拉强度根据文献[21]建议的普通混凝土抗拉强度和抗压强度的关系计算,如下式所示
(7)
混凝土的单轴应力-应变关系曲线如图8所示。
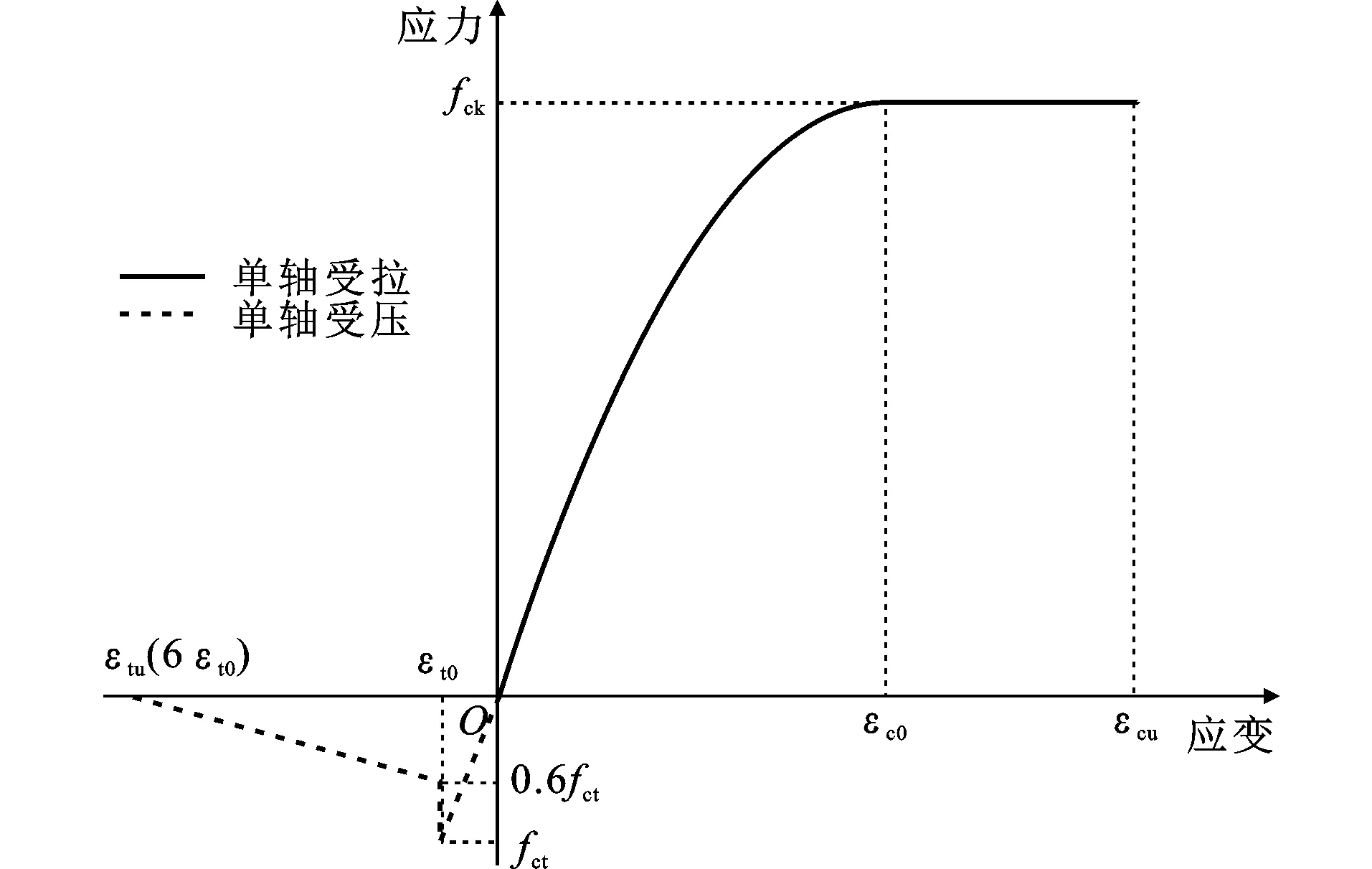
图8混凝土的应力-应变曲线Fig.8Stress-strain Curve of Concrete
(2)角钢:角钢单调本构关系采用理想弹塑性模型,模型中材料屈服强度和初始弹性模量采用表2中试验结果。
3.2 单元介绍及界面作用的实现
混凝土采用8节点Solid65单元模拟,该单元可模拟混凝土的开裂、塑性变形等功能,计算时关闭压碎功能。角钢采用8节点Solid185单元模拟,具有弹性、塑性等特性。角钢与混凝土接触面插入面-面接触单元。角钢表面为刚性目标面,目标单元采用Targe170单元模拟,见图9(a)。混凝土面为柔性接触面,接触单元采用Conta174单元,见图9(b)。

图9接触对Fig.9Contact Pair
化学胶结力和摩擦力由库仑摩擦模型[21]实现。在接触面滑动前,界面处于黏合状态,当界面间黏聚力COHE与初始摩擦力μP之和超过容许剪应力τmax后,进入滑动状态,见图10,μ为摩擦因数。
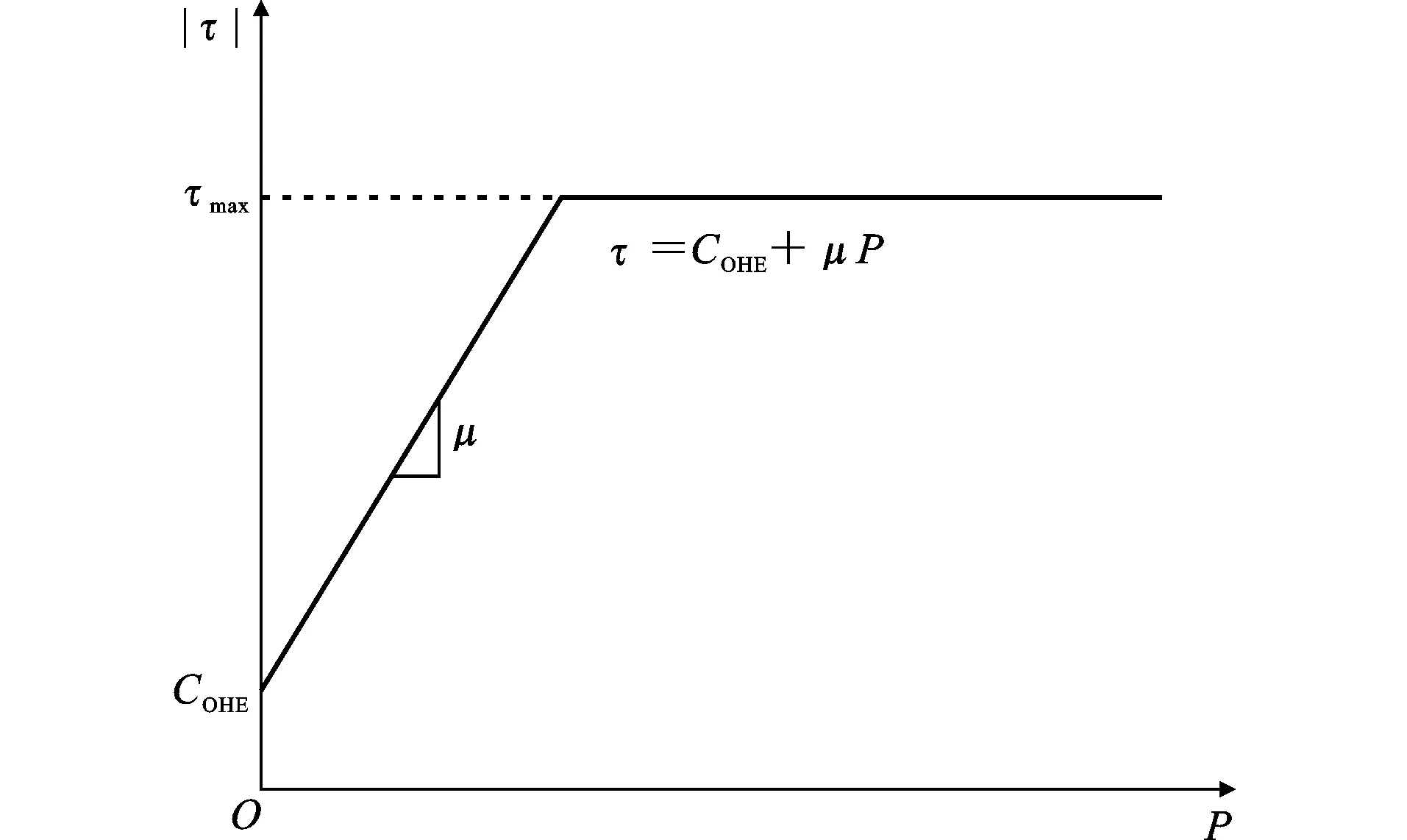
图10库仑摩擦模型Fig.10Coulomb Friction Model
本文COHE取值参考试验初始滑移荷载对应的黏结应力,具体取值见表6。
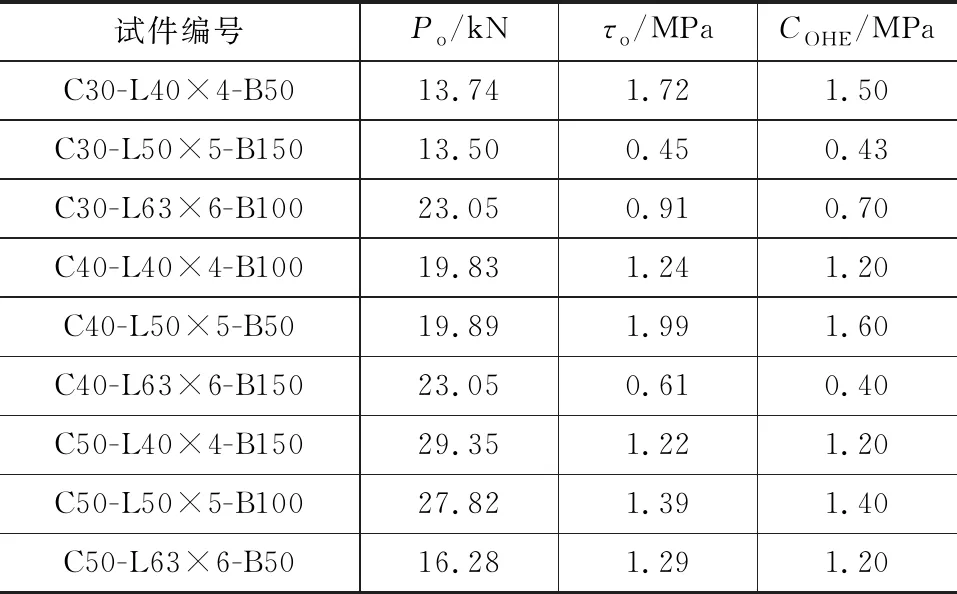
表6有限元模型COHE取值Tab.6Values of COHE in Finite Element Model
摩擦因数μ初值取0.45[22],当加载端荷载达到极限滑移荷载后,摩擦因数随界面滑移值变化而呈负指数衰减[23],得到本文采用的摩擦因数衰减模型,如式(8)所示。由于摩擦因数在计算荷载步间进行变化,而重启动分析可以实现在原来分析的基础上继续计算,故摩擦因数的衰减过程由重启动分析实现。
(8)
式中:η为衰减系数,根据试算确定。
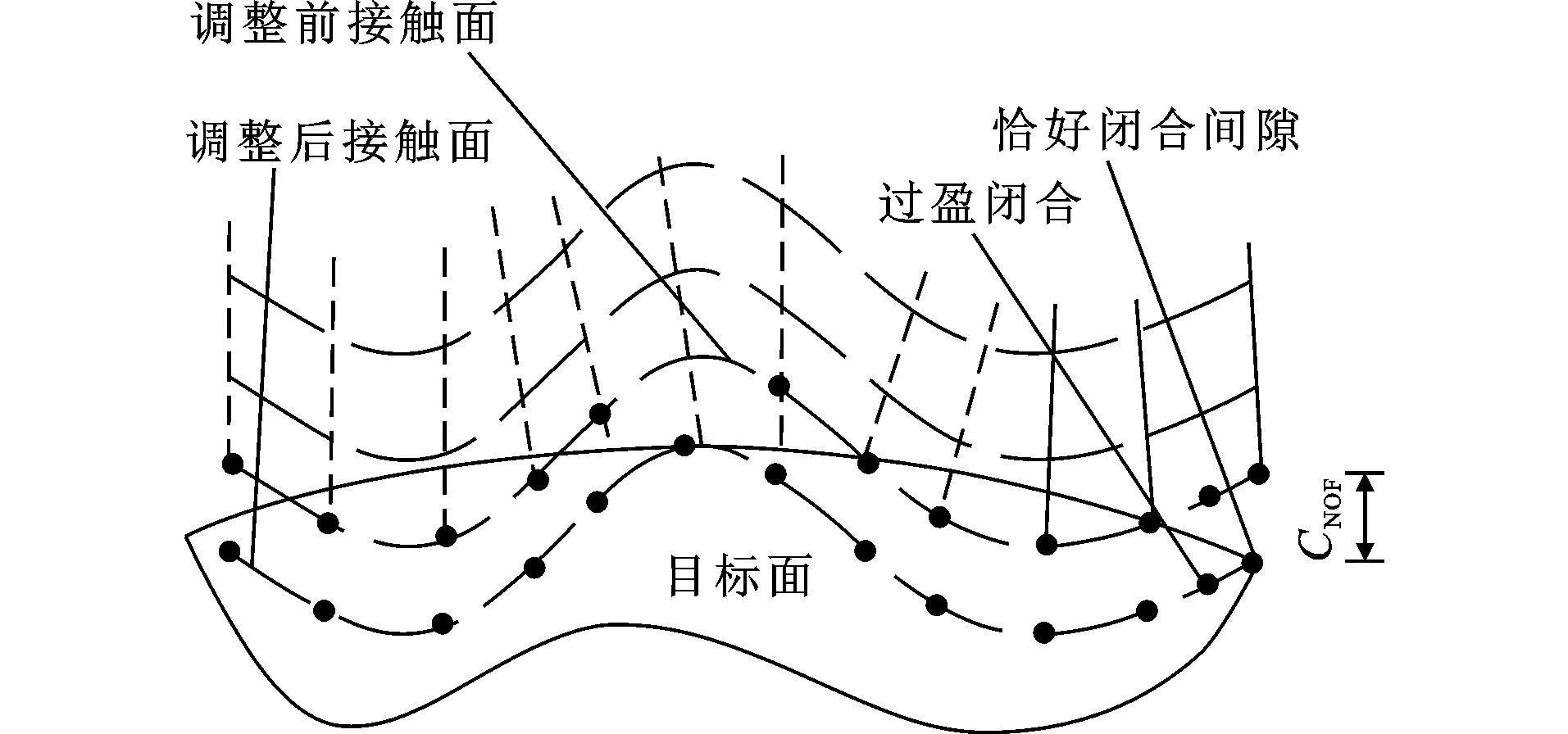
图11实常数CNOF调整初始接触Fig.11Adjust Initial Contact by Real Constant CNOF
机械咬合力由面-面接触单元适用的过盈装配[21]实现。组成过盈连接后,混凝土为“包容件”,角钢为“被包容件”。由于接触面处的弹性变形和过盈装配量,在接触面产生法向压力。当加载端承受外荷载时,接触面靠法向压力所产生的摩擦力或摩擦力矩来传递荷载。过盈装配通过实常数CNOF指定接触面偏移(图11)实现,且ANSYS能够自动闭合间隙或减少初始穿透。本文过盈值CNOF取值范围为0.3~0.6。
3.3 有限元模型
有限元计算模型如图12所示。求解时约束混凝土下底面节点的竖向自由度,将角钢顶面节点耦合于一点(角钢形心正上方),施加位移荷载。

图12有限元模型Fig.12Finite Element Model
3.4 荷载-滑移曲线FEM计算值与试验值比较
图13为模拟所得加载端荷载-滑移曲线,根据试验中试件所采用的角钢规格分3组列出。
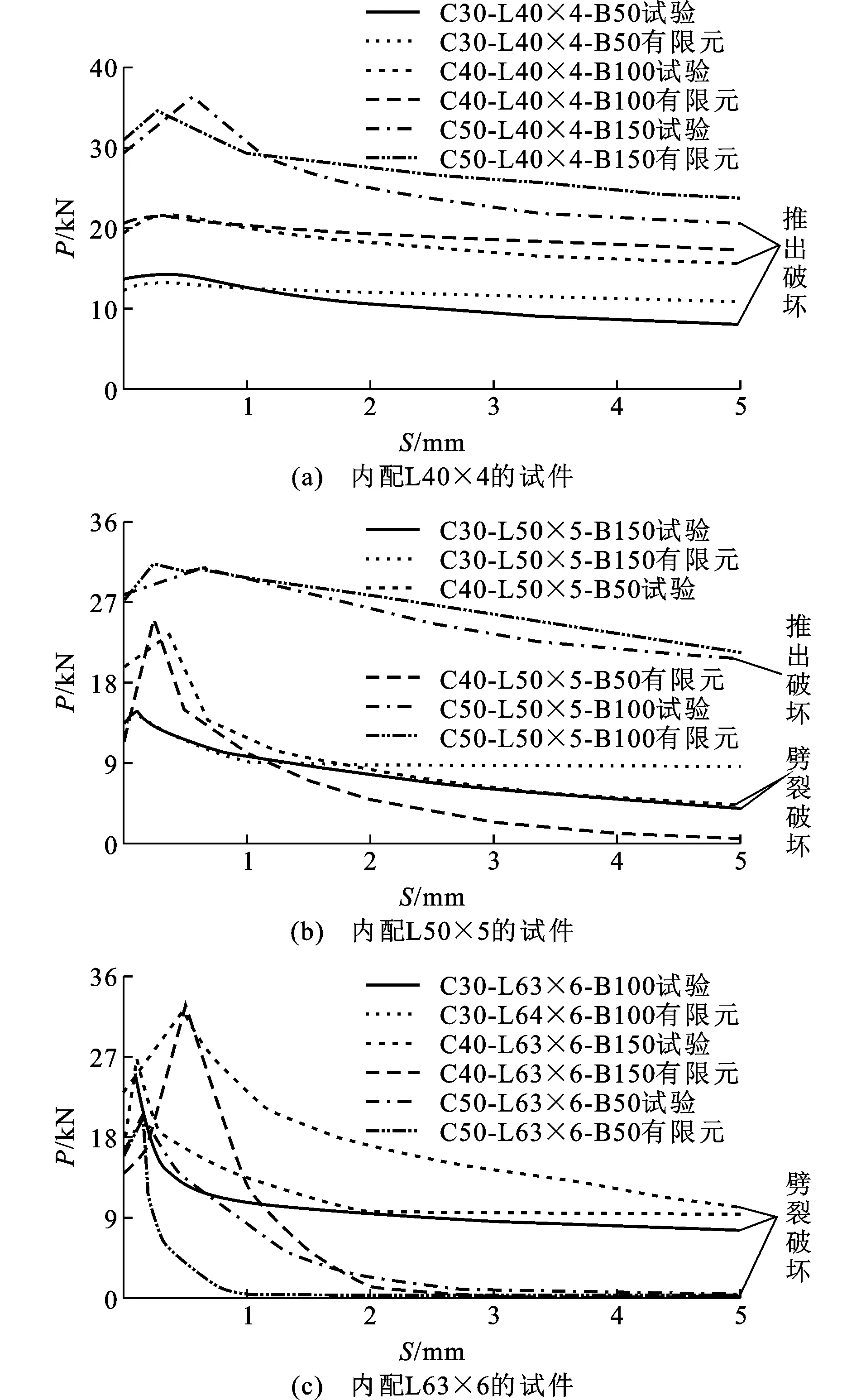
图13荷载-滑移曲线FEM计算值与试验值比较Fig.13Comparisons of FEM Calculation Values and Test Values of Load-slip Curves
图13表明,推出破坏试件整体吻合较好,而由于试验过程中存在误差,试件加工也存在偏差,试件劈裂破坏的程度不稳定,法向压力有差异,因此劈裂破坏试件下降段计算值与试验值相差略大。
3.5 黏结机理分析
根据试验结果(图5)与有限元分析结果(图13),加载端荷载-滑移曲线趋势可归纳为图14中的典型曲线(Sr为残余滑移,Pr为残余荷载),包括胶结段(Oa)、上升段(ab)、下降段(bc)和残余段(cd),各阶段黏结机理可阐述为:

图14典型P-S曲线Fig.14Typical Curves of P-S
(1)胶结段(Oa):初加载时,黏结界面无相对滑移,加载端存在固定传递长度ltr,b[24],传递长度区域混凝土和角钢出现相对滑移趋势,经过传递长度区进入非传递区,角钢与混凝土的应变相同,共同承受轴向压力。传递长度ltr,b区域内和非传递区局部黏结界面化学胶结力和静摩擦力共同发挥作用。Oa段黏结滑移机理见图15。

图15Oa段黏结应力分布Fig.15Distribution of Bond Force at Oa Section
(2)上升段(ab):当加载端荷载达到初始滑移荷载Po时,传递长度区域发生滑移,如图16(a)所示,化学胶结力丧失且由于角钢表面不能绝对平整,角钢与混凝土挤压产生法向压力,进而产生动摩擦力和机械咬合力,产生机理由见图17。
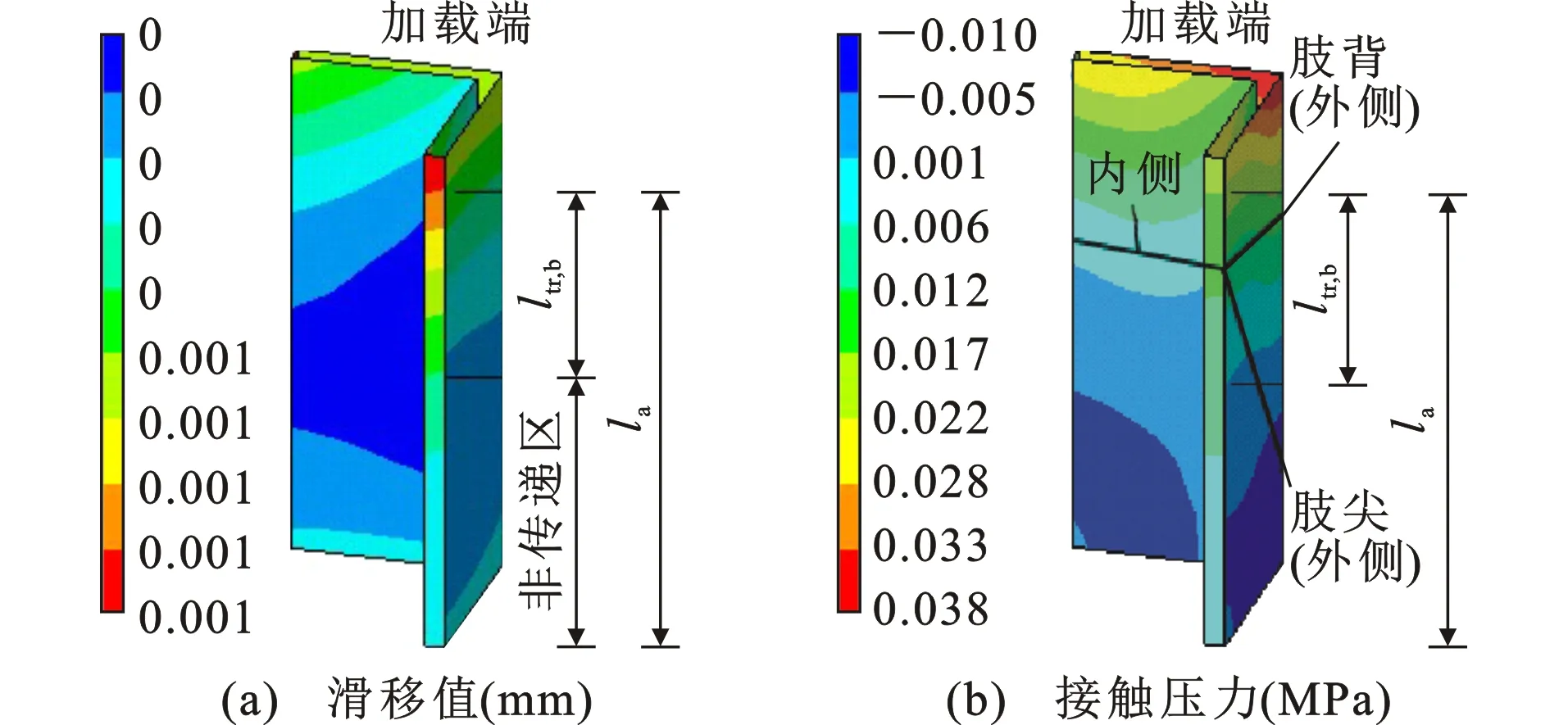
图16初始滑移荷载对应的黏结界面状态Fig.16Bond Interface State Corresponding to Initial Slip Load
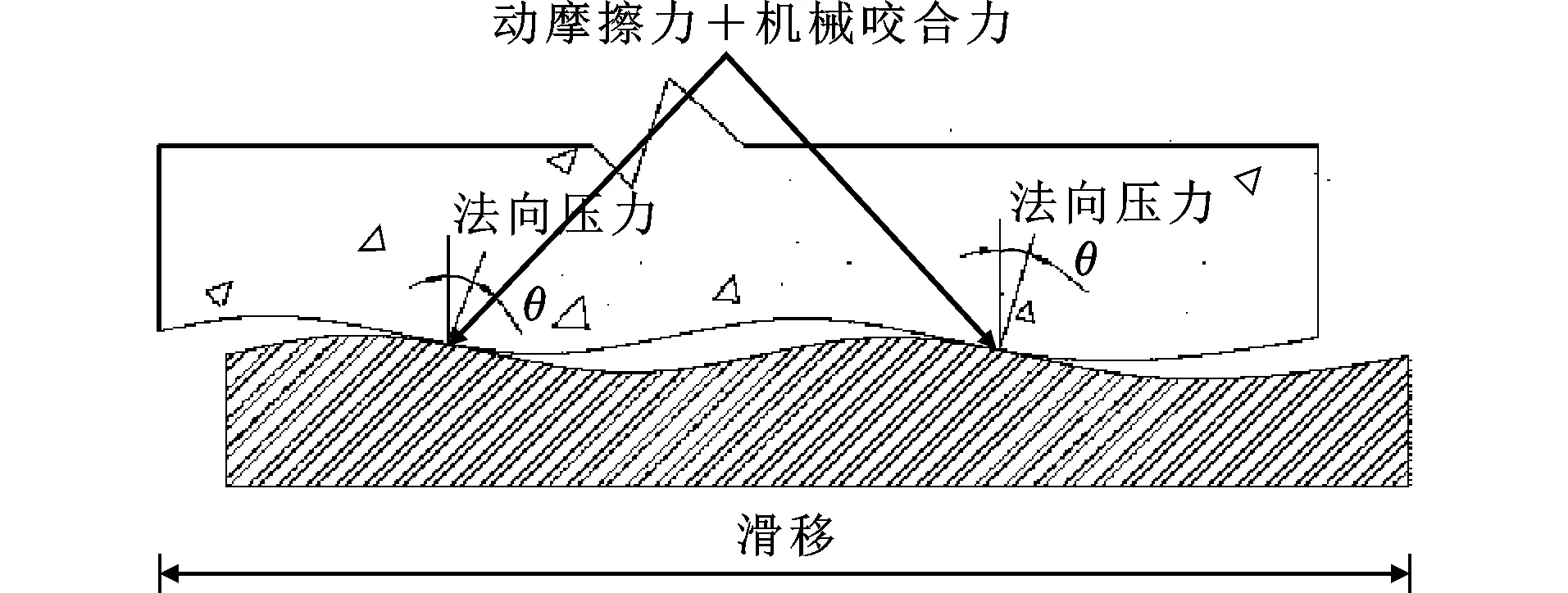
图17界面挤压Fig.17Interface Extrusion
初始滑移时接触压力分布如图16(b)所示,对相同横截面而言,越靠近肢背处的接触压力越大,角钢外侧的接触压力大于内侧。应当指出,对于工程应用的角钢混凝土构件,当混凝土保护层厚度足够大时,若混凝土仍整体向中心收缩,靠近肢背处约束作用被加强,角钢内侧约束作用被减弱。对于内配工型钢、H型钢试件,型钢翼缘外表面的黏结应力约为内表面和腹板表面黏结应力的2倍[8-9]。因此型钢截面形式和混凝土收缩作用均是影响黏结应力分布的重要因素。
随着加载端荷载增大,靠近加载端部分混凝土被剥离,仅有摩擦力,传递长度向非传递区移动,并逐步发展为全截面滑移。总黏结力(动摩擦力和机械咬合力)持续增大至极限黏结强度。ab段黏结滑移机理如图18所示。
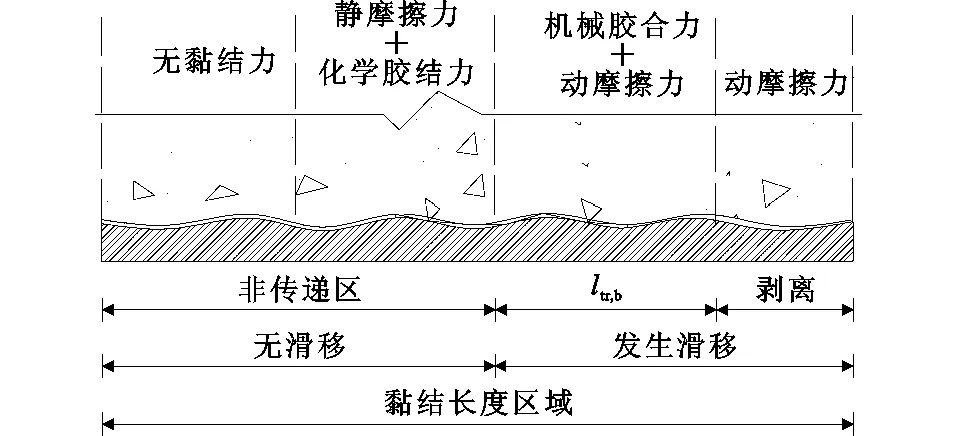
图18ab段黏结应力分布Fig.18Distribution of Bond Force Distribution at ab Section
(3)下降段(bc):加载端与自由端摩擦应力梯度达到最大,见图19(a)。随着滑移量增加,混凝土表面凸出的混凝土被剥离带出,填充角钢和混凝土内凹的区域,自由端滑移后会带出部分已破坏的混凝土碎屑,混凝土对角钢的包裹作用变小,摩擦应力梯度逐步减小并伴随较大滑移量,如图19(b)所示。bc段滑移机理如图20所示。

图19不同滑移值对应的摩擦应力(单位:MPa)Fig.19Friction Stress Corresponding to Different Slips (Unit:MPa)
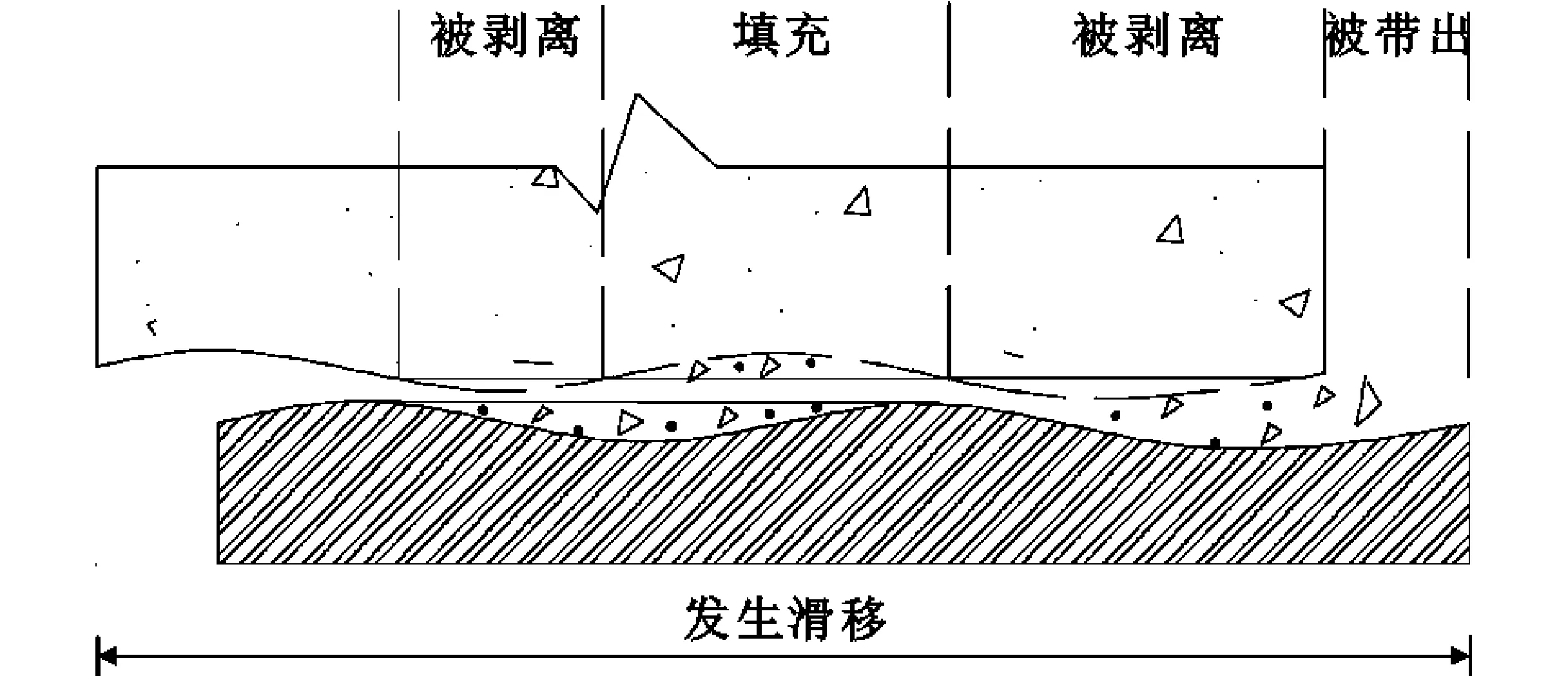
图20bc段滑移机理Fig.20Slip Mechanism of bc Section
应当指出,当混凝土约束较弱时,裂缝扩展使得试件沿着角钢肢尖发生劈裂破坏。本文试验表明,混凝土保护层厚度较小时,发生瞬时的混凝土劈裂破坏。因角钢的肢尖存在致裂作用,故在工程应用中应当着重考虑。
(4)残余段(cd):黏结界面被逐渐磨平,界面黏结应力趋于稳定。
3.6 传递长度计算方法
有限元计算得到的各试件传递长度ltr,b值如图21所示,定义先发生滑移的界面长度为传递长度值。
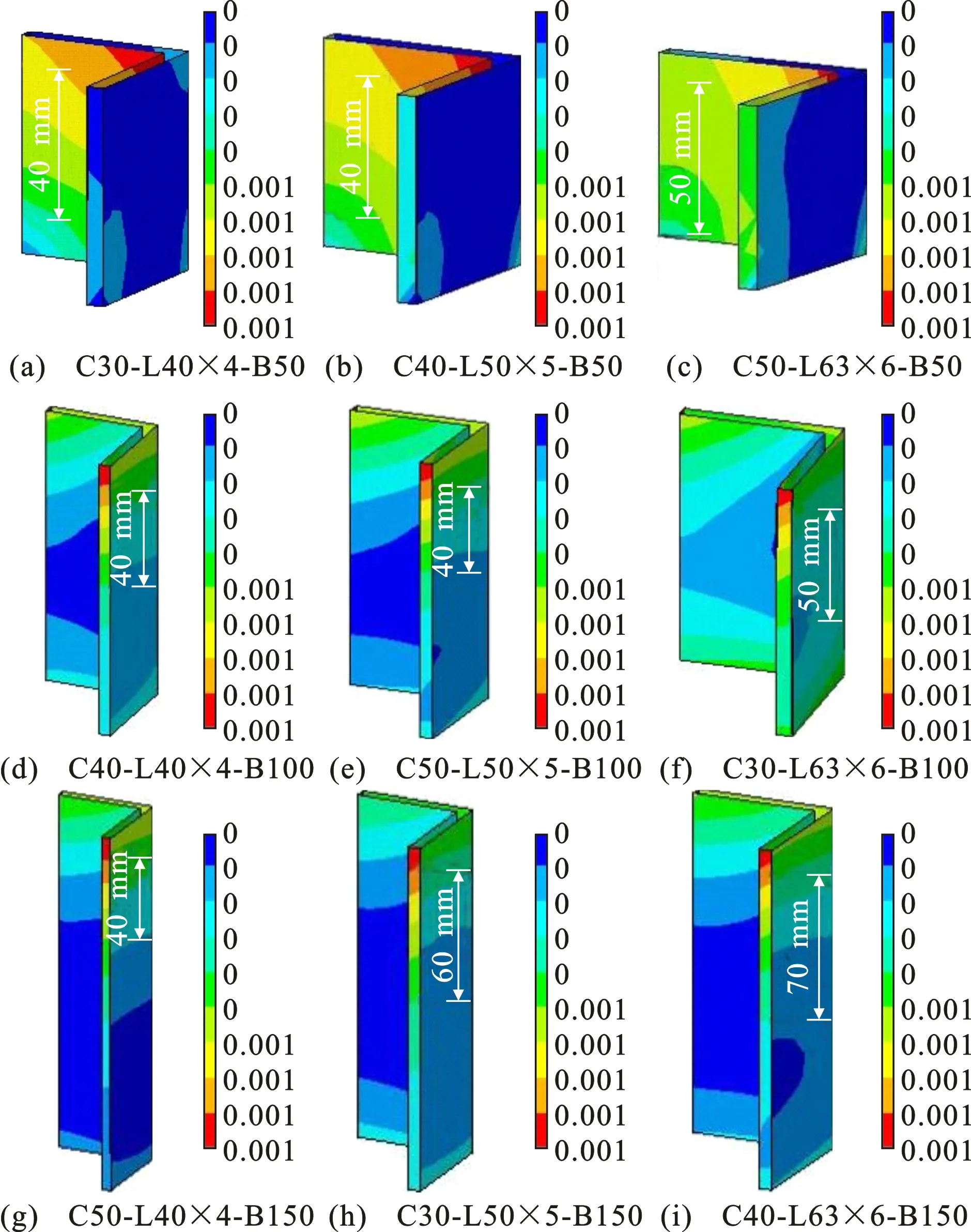
图21传递长度有限元计算结果(单位:mm)Fig.21Results of FEM Calculation of Transfer Length (Unit:mm)
建立传递长度与混凝土抗压强度fcu、保护层厚度C、角钢肢长L、初始滑移荷载对应的黏结应力τo、钢材弹性模量Es与混凝土弹性模量Ec之比相关关系,如式(9)所示,Ec根据《混凝土结构设计规范》确定[20]。传递长度公式计算值与有限元计算值对比见图22(平均值为1.003 3,标准差为0.076 93,变异系数为0.076 67),整体误差较小。
(9)
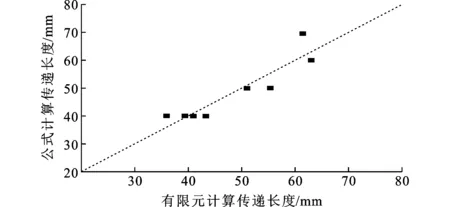
图22传递长度对比结果Fig.22Comparison Results of Transfer Length
4 结语
(1)极限黏结强度随混凝土强度提高和保护层厚度增大而增大,但随黏结长度增大而线性降低。
(2)角钢肢尖存在致裂作用,工程应用中应予以重视。试件发生劈裂破坏后,极限黏结强度明显降低,承载能力急剧下降。保护层厚度较小时,试件更容易发生劈裂破坏,建议着重考虑保护层厚度的取值。
(3)有限元模型较好地模拟了界面黏结力的构成和摩擦力随滑移发生变化的过程。试验结果与有限元分析结果均表明,加载端荷载-滑移曲线可分为胶结段、上升段、下降段和残余段。
(4)数值模拟结果表明,加载初期固定传递长度区域产生滑移趋势。随着荷载增大,黏结界面加载端向自由端逐步发生滑移,传递长度保持不变。传递长度值与混凝土抗压强度、保护层厚度、角钢肢长、初始滑移荷载对应的黏结应力、钢材与混凝土弹性模量之比相关。
