高温后钢筋-混凝土界面黏结性能分析

周默苇，高皖扬,2，胡克旭

(1. 上海交通大学 船舶海洋与建筑工程学院，上海 200240； 2. 上海交通大学 海洋工程国家重点实验室， 上海 200240； 3. 同济大学 结构防灾减灾工程系，上海 200092)

0 引 言

火灾发生频率高居各自然灾害之首，其中建筑火灾占80%左右[1]。火灾作用后，钢筋混凝土结构遭受一定程度的损伤甚至破坏，其灾后残余性能和结构损伤程度决定了灾后加固修复决策。

现有试验研究表明，高温后钢筋力学性能较易恢复，而钢筋-混凝土界面黏结性能劣化显著。随着温度升高至600 ℃，钢筋屈服强度的劣化并不明显，然而界面黏结强度在300～400 ℃时开始发生严重劣化，600 ℃时已降低至常温下黏结强度的40%左右。因而火灾后钢筋混凝土构件残余性能的评估多取决于高温后钢筋-混凝土界面黏结性能的准确表征。若忽略界面劣化的影响，将导致灾后构件残余性能评估的不准确。

自20世纪80年代起，众多学者采用拉拔试验研究常温下钢筋的锚固性能及钢筋-混凝土界面的黏结性能，所涉及的试验参数包括：钢筋品种和直径、锚固长度、混凝土等级与抗拉强度、混凝土保护层厚度等[2-7]。同时为了将试验结果推广至实际工程应用，许多学者基于试验数据建立了界面黏结强度的统计学模型，但拉拔试验并无统一标准，不同的试验设计导致试验结果有较大的离散性，统计学模型难以涵盖所有情况。此外，一些研究者也开展了拉拔试验研究高温后钢筋-混凝土界面黏结性能的劣化，并基于试验数据建立界面黏结强度模型，但高温后钢筋-混凝土界面的劣化及破坏机理尚未明晰，仍亟待大量研究。

本文建立了高温后钢筋-混凝土黏结界面的力学分析模型，该模型基于Tepfers[8]提出的厚壁圆筒模型，将包围在钢筋周围的混凝土保护层作为一个受到内压力的厚壁圆筒进行受力分析。当钢筋拉拔力逐渐增加时，混凝土中出现裂缝，厚壁圆筒被分为开裂内层和未开裂外层两部分，假定在部分开裂混凝土中形成径向裂缝并考虑其抗拉软化效应[9]。同时模型考虑了高温后混凝土材料性能劣化，包括遭受高温损伤后混凝土抗拉强度、弹性模量及断裂能的变化。基于该分析模型建立了高温后钢筋-混凝土界面黏结强度模型及界面黏结应力-端部滑移关系。通过与已有高温后钢筋拉拔试验结果进行对比，验证了理论分析模型的准确性。

1 理论分析模型

该分析模型对高温后钢筋的拉拔试验(也称钢筋-混凝土界面黏结性能试验)进行分析。模型将钢筋周围的混凝土保护层简化为受内部均匀径向压力的厚壁圆筒。随着外荷载(钢筋拉拔力)增加，内压力增大，混凝土部分开裂，将混凝土分为开裂内层和未开裂外层2个圆筒。假定对开裂内层的混凝土采用基于弥散裂缝的抗拉软化模型进行分析[9]，同时考虑高温后材料性能的劣化，推导出高温后钢筋拉拔破坏过程及界面黏结强度模型。

1.1 受力分析

在拉拔试验过程中，变形钢筋与混凝土之间的黏结力主要由机械咬合力提供。钢筋肋与混凝土接触面上产生垂直于肋斜面的压应力，其水平分力为阻止钢筋被拔出的黏结应力τ，径向分力为外围混凝土提供的径向挤压应力p，如图1所示。当钢筋肋斜面倾斜角度为α时，可得τ与p之间的关系为

τ=ptan(α)

(1)

式中：α一般取45°[8-9]，此时τ=p。

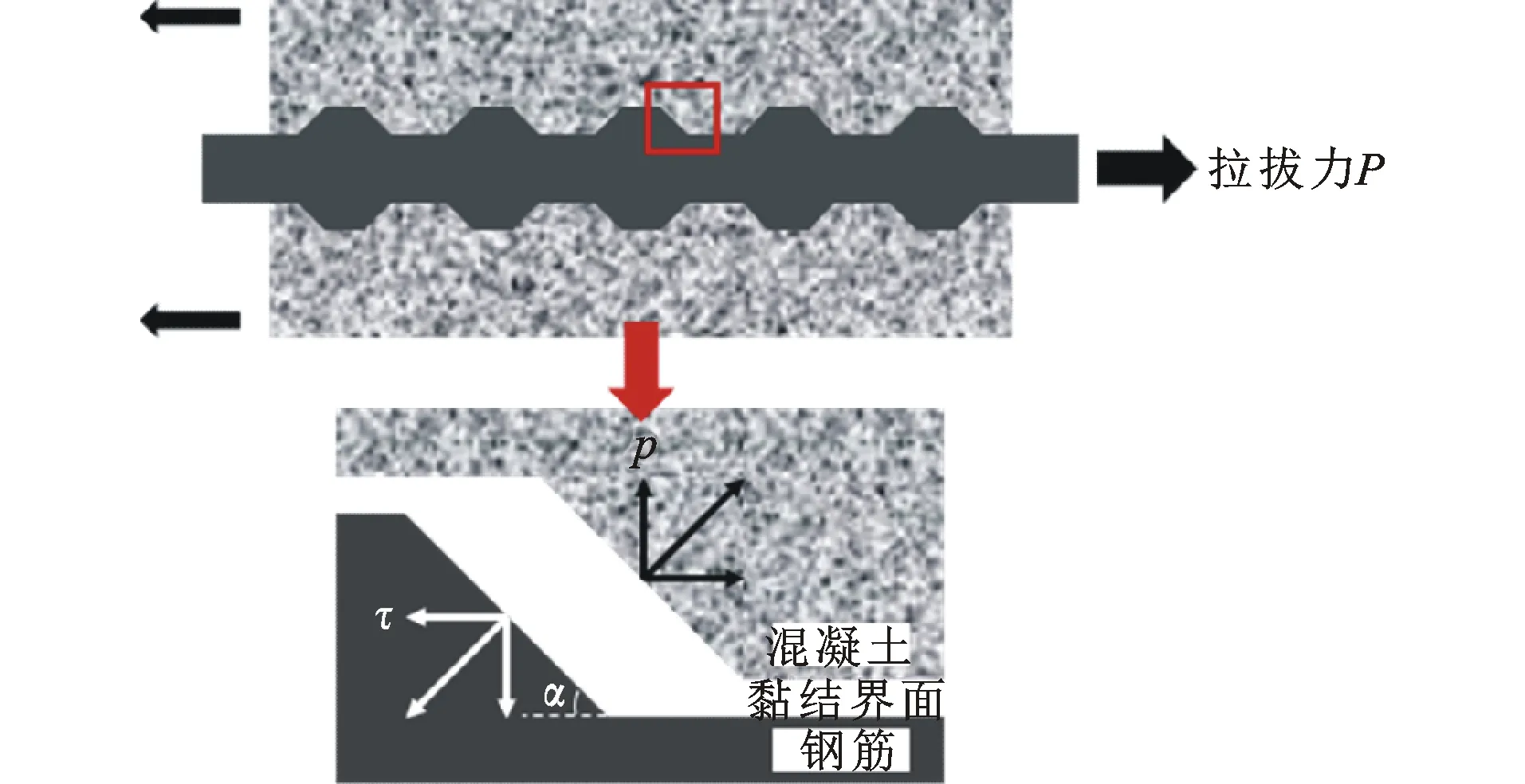
图1钢筋-混凝土黏结界面受力分析Fig.1Stress Analysis of Steel Bar-to-concrete Interface

混凝土受到钢筋的反作用力时，该径向压应力由混凝土中的环向拉应力平衡。当拉应力超过混凝土抗拉强度时发生开裂。随着外荷载的增加，界面上的黏结应力逐渐达到峰值，即为黏结强度。之后黏结应力开始下降，试件发生劈裂破坏。

将拉拔试件简化为一个受到内压力的厚壁圆筒，见图2，其中，Ri为开裂半径，Rb为钢筋半径，Rc为圆筒外半径，是从钢筋中心量测的混凝土保护层厚度，取试件保护层最薄处尺寸。当外荷载增加时，混凝土产生径向劈裂裂缝。根据不同的应力状态，圆筒可被分为内外2个部分：在外层部分(Ri≤r≤Rc)，裂缝尚未出现，混凝土仍处于线弹性阶段，pi为径向压应力；在内层部分(Rb≤r≤Ri)，裂缝出现并沿径向开展，拉应力超过了抗拉强度，混凝土处于抗拉软化阶段，在内外层之间的临界面(r=Ri)上，混凝土拉应力等于抗拉强度。

1.1.1 开裂外层

对厚壁圆筒外层部分进行受力分析，其处于弹性阶段，界面r=Ri上受到径向压应力pi。由于此界面上混凝土环向拉应力σt等于混凝土抗拉强度fct，运用弹性力学理论[10]，可得径向压应力pi为

(2)

图2混凝土保护层的厚壁圆筒模型Fig.2Thick-wall Cylinder Model of Concrete Cover

1.1.2 开裂内层

对厚壁圆筒内层部分进行受力分析，在钢筋-混凝土黏结界面上拉应力达到抗拉强度，混凝土出现裂缝并沿径向开展，此时混凝土中环向拉应力σt≥fct，应考虑其受拉应力-应变本构关系的软化特征。本模型采用双折线形受拉应力-裂缝宽度(σt-w)曲线(图3)表征混凝土的软化特征[9]。图3中，β为受拉应变软化模型中的参数，依据CEB-FIP Model Code1990[11]，取0.15，wu为拉应力为0时的极限裂缝宽度，w1为拉应力为βfct时的裂缝宽度，常取w1=2wu/9[12]。两折线与坐标轴所包围的面积即为断裂能Gf，由此可得极限裂缝宽度的计算式为

(3)

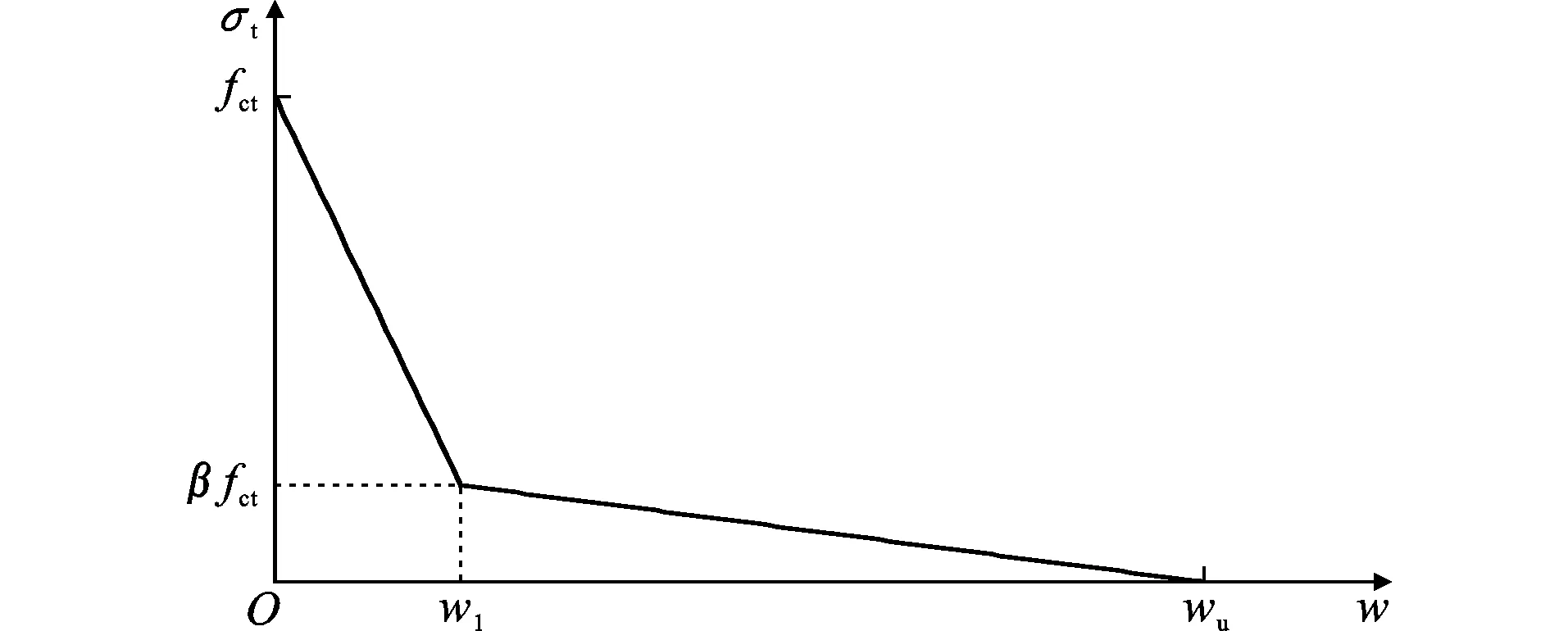
图3受拉应力-裂缝宽度曲线Fig.3Tensile Stress Versus Cracking Width Curve

将受拉应力-裂缝宽度关系转变为受拉应力-应变本构关系，混凝土拉应变εt=w/hc，hc为混凝土裂缝带宽度的特征值，一般取5倍的混凝土粗骨料最大尺寸，若试验未提供粗骨料尺寸，可近似取hc=100 mm[13-14]。

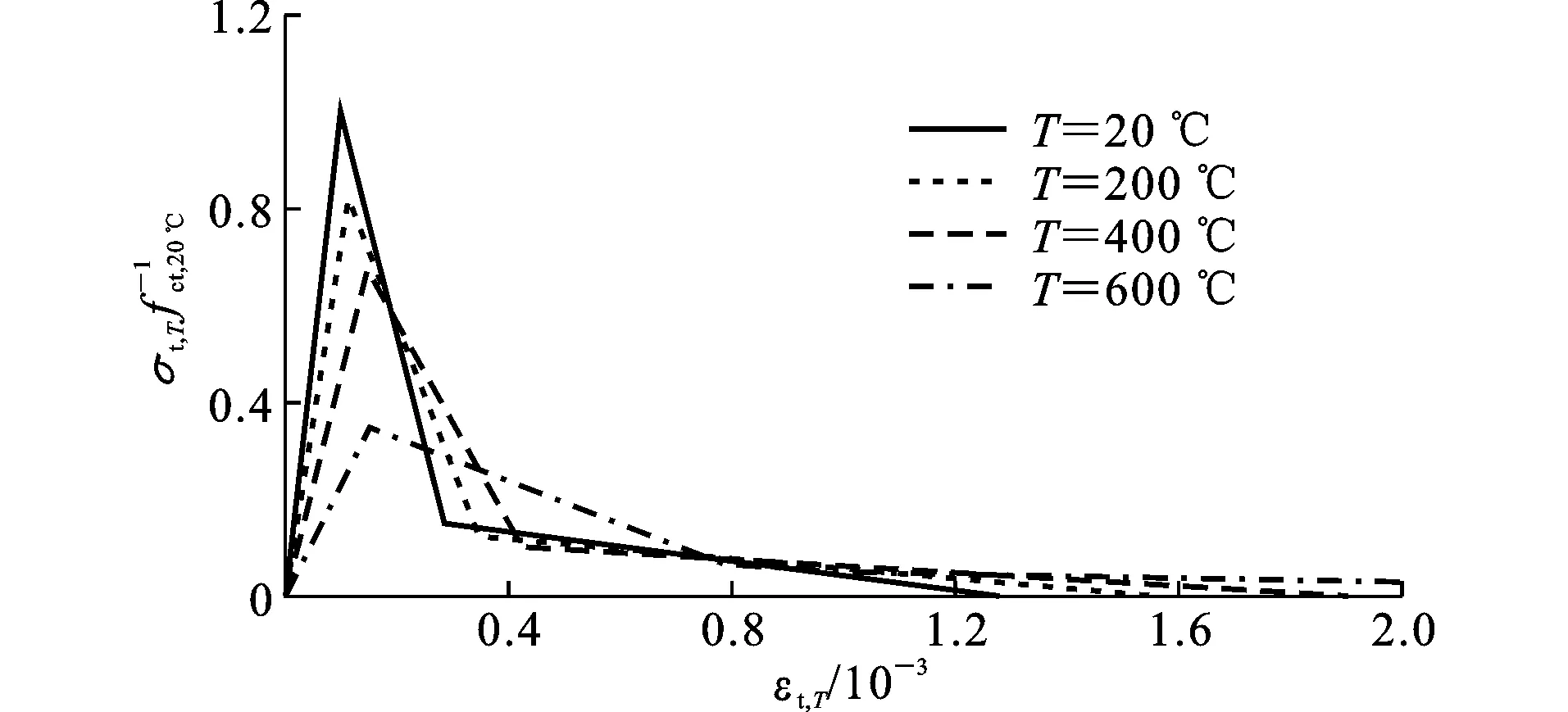
图4常温及高温后混凝土受拉应力-应变本构关系Fig.4Tensile Stress-strain Constitutive Relations of Concrete at Room Temperature and After Exposure to Elevated Temperatures

经受常温(20 ℃)和不同高温T损伤(如200，400，600 ℃)的混凝土受拉应力-应变本构关系如图4所示。混凝土达到峰值应力前为线弹性；当拉应力达到抗拉强度时，混凝土软化阶段采用双折线模型。本构关系式如下

(4)

式中：εt为混凝土拉应变；Ec,T，fct,T分别为混凝土遭受不同高温T损伤后的弹性模量与抗拉强度；εct,T为混凝土遭受不同高温T损伤后的开裂应变，εct,T=fct,T/Ec,T；εu,T为混凝土遭受不同高温T损伤后，相应于抗拉强度为0时的极限拉应变，εu,T=wu,T/hc；ε1,T为混凝土遭受不同高温T损伤后，相应于抗拉强度为βfct,T时的拉应变，ε1,T=2εu,T/9。

1.1.3 开裂界面

随着裂缝径向开展，开裂半径Ri从Rb向Rc靠近，如图5所示隔离体，在任一开裂截面可以建立如下的平衡方程

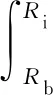
(5)

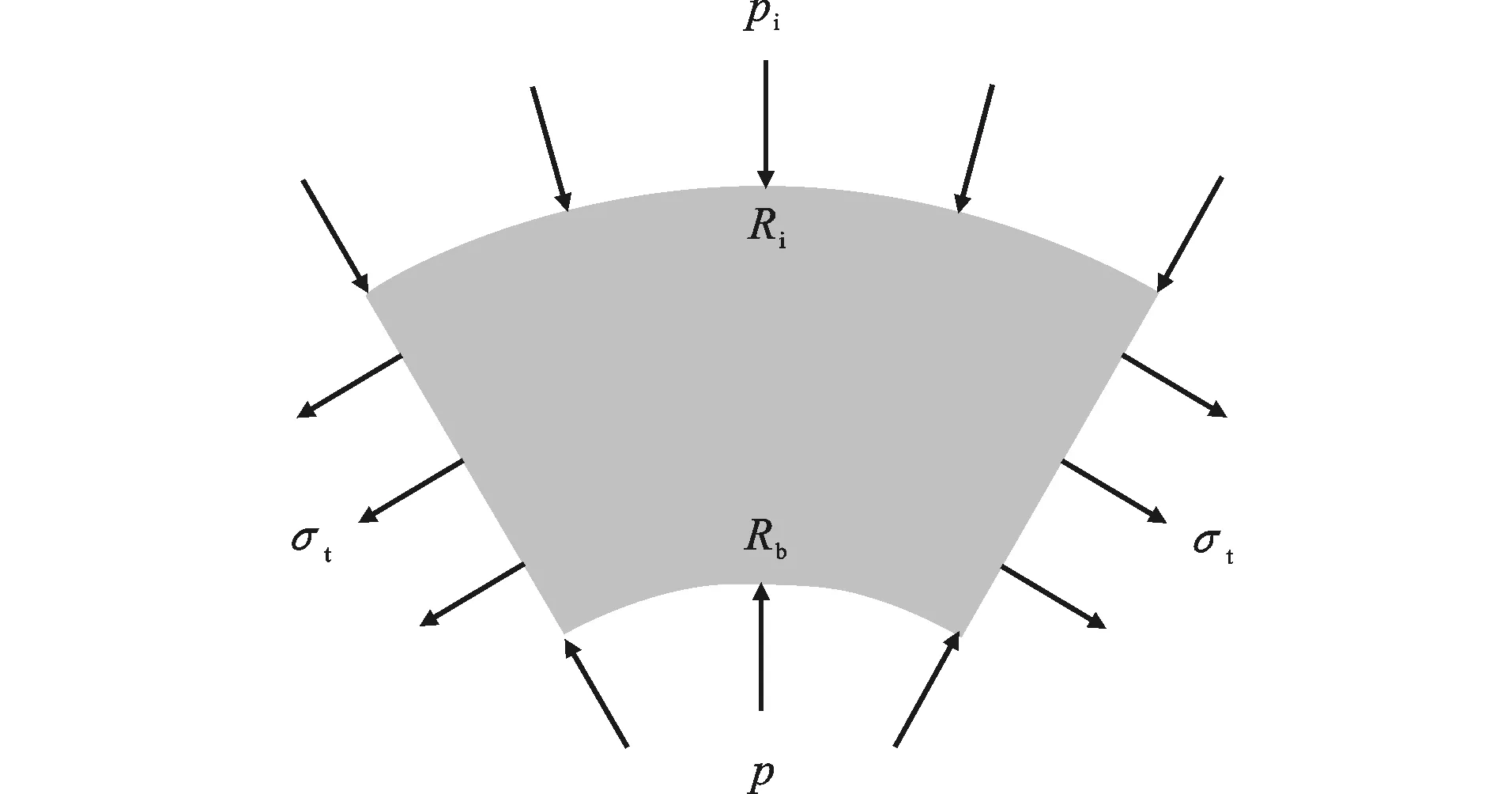
图5内层开裂部分混凝土受力状态Fig.5Stress State of Inner Cracked Concrete

在r=Ri处，混凝土拉应力达到抗拉强度，应变为混凝土的弹性极限应变εct，εct=fct/Ec。假定在部分开裂的混凝土中，其径向位移r为常量[9]，同时考虑到内外层两部分的变形协调(不考虑泊松效应)，可得到δr=Riεct=rεt，因而拉应变和半径成反比，即

(6)

1.2 高温后混凝土力学性能

由上述受力分析可知，混凝土材料性能影响钢筋-混凝土界面的黏结性能，高温损伤导致混凝土材料力学性能劣化，因此，表征钢筋-混凝土界面残余黏结性能，需准确考虑高温后混凝土的弹性模量、抗拉强度、断裂能等材料性能。

1.2.1 弹性模量

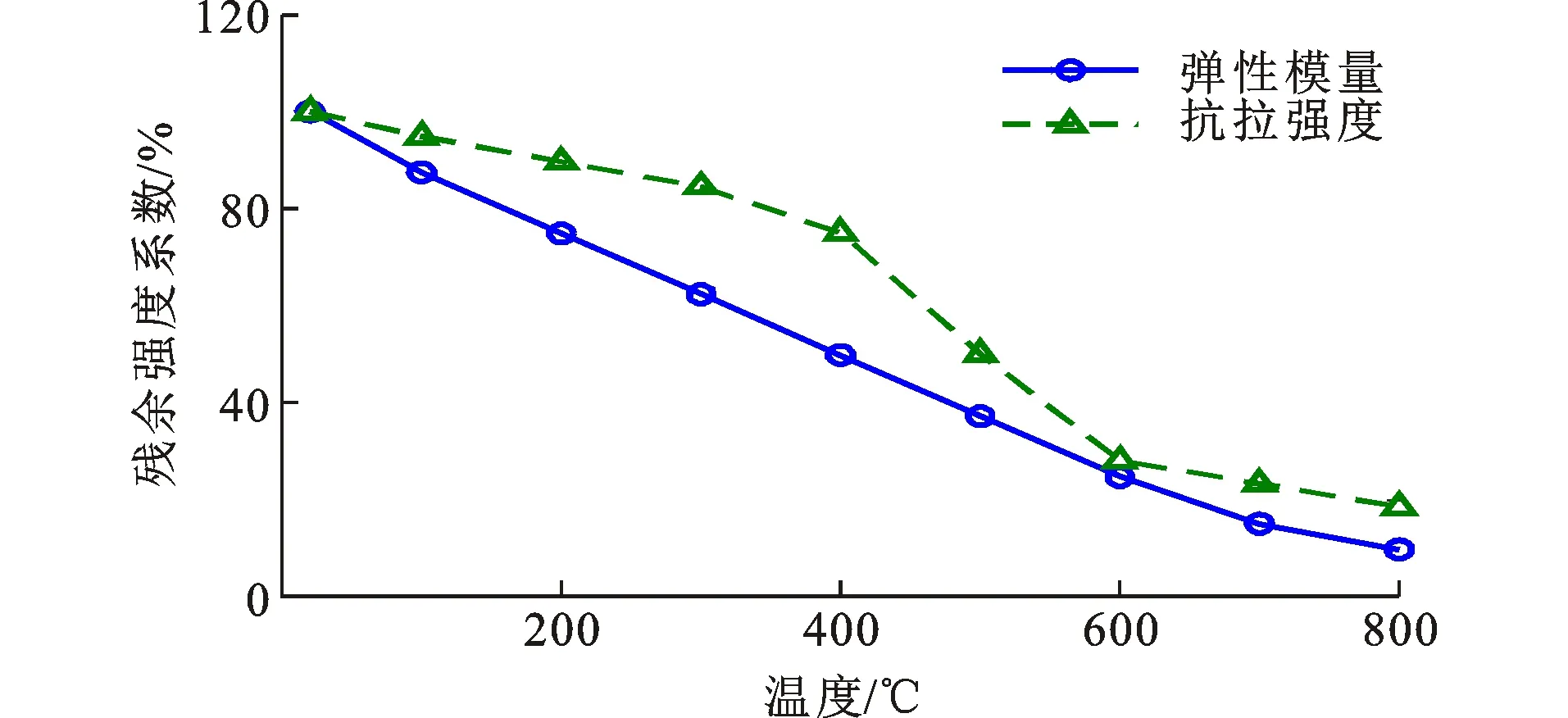
图6高温后混凝土残余力学性能Fig.6Residual Mechanical Properties of Concrete

1.2.2 抗拉强度

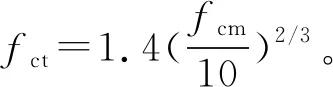
1.2.3 断裂能

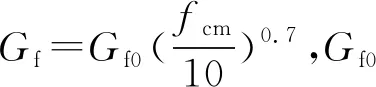
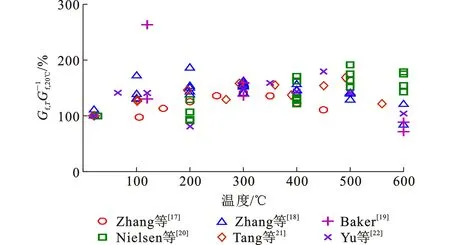
图7高温后混凝土断裂能Fig.7Fracture Energy of Concrete After Exposure to Elevated Temperatures

高温后混凝土断裂能的试验数据较少，且已有采用的试验方法均不相同，图7中列出了Zhang等[17-18]、Baker[19]、Nielsen等[20]、Tang等[21]、Yu等[22]的试验数据，可以看出，高温后混凝土的断裂能变化趋势不明显，因此本文将混凝土的断裂能考虑为定值，不考虑高温后混凝土断裂能的变化[23]。

1.3 计算黏结强度

在计算公式(5)中的积分式时，需要确定已开裂混凝土所处的拉伸软化阶段。εtb为钢筋-混凝土界面(r=Rb)处的拉应变，其所处的应力状态有2种可能发生的情况(以常温为例)：εct≤εtb≤ε1[图8(a)]或ε1<εtb≤εu[图8(b)]。

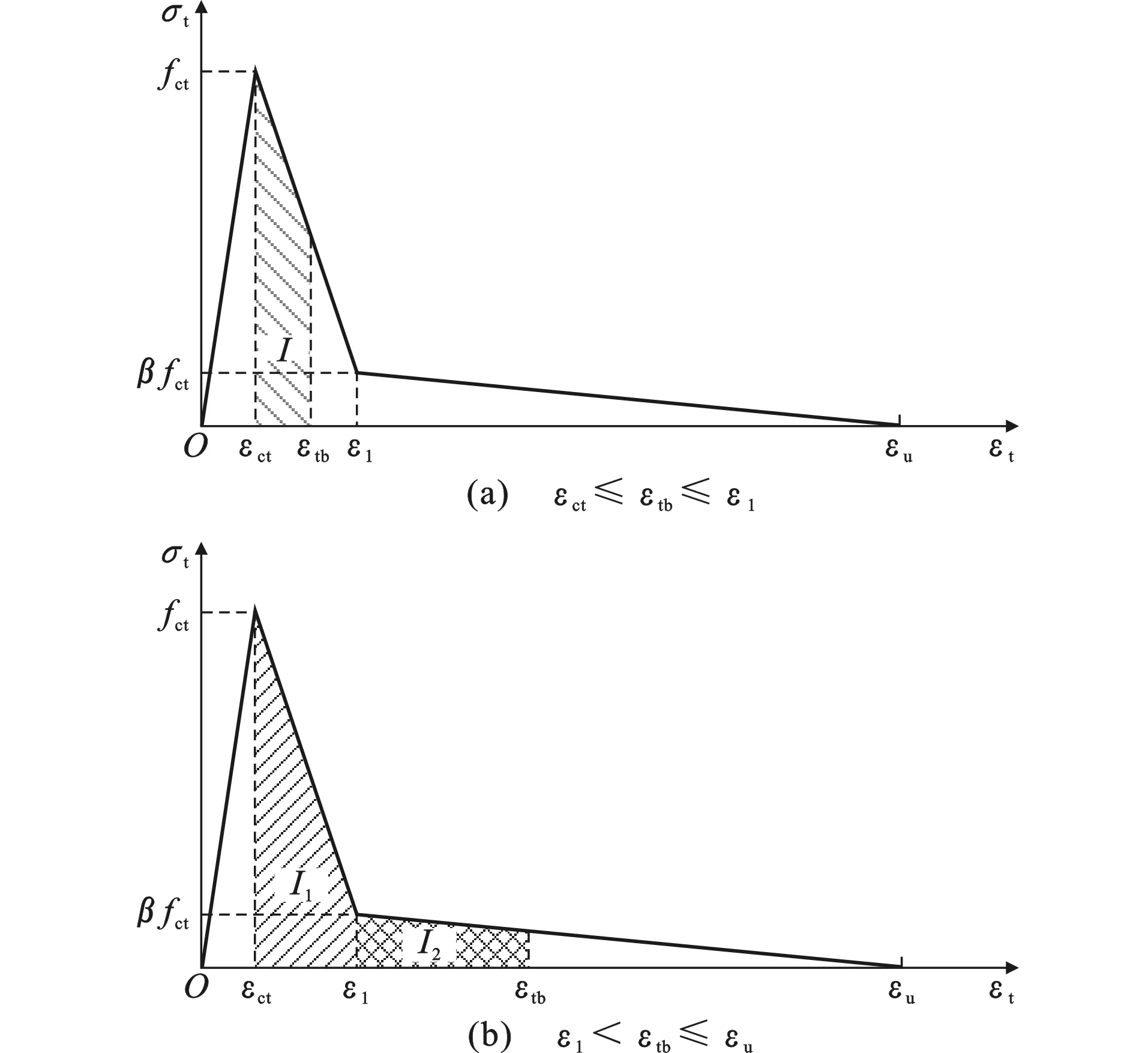
图8应变εtb所处的2种情况(以常温为例)Fig.8Two Strain Conditions of εtb (Taking Case at Room Temperature as an Example)

利用变形协调方程式(6)可得到εtb和εct之间的关系如下

(7)

因为开裂半径Ri介于Rb与Rc之间，所以不等式Ri/Rb≤Rc/Rb始终成立。对于给定的某个钢筋拉拔试件，可计算出混凝土保护层半径和钢筋半径的比值Rc/Rb，利用Rc/Rb的大小来估计混凝土应变所处的阶段。以下分别考虑应力处于2种不同阶段的情况。

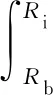
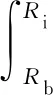
综上，可得到径向应力p为

(8)

为求应力p的最大值，将式(8)对Ri求导，令导式为0，解得开裂半径Ri,max，即当Ri=Ri,max时p取极值。将Ri,max代入式(8)，可得最大径向应力pmax为

(9)

当发生劈裂破坏时，由式(1)可知，最大黏结应力等于最大径向压应力，即τmax=pmax。

2 黏结-滑移性能

本节对高温后钢筋-混凝土界面的黏结应力-端部滑移关系进行分析。随着外荷载的增加，界面的黏结应力不断增大，钢筋与混凝土间发生相对滑移。下文分别建立了混凝土开裂前后钢筋拉拔试件的黏结应力-端部滑移关系。

2.1 混凝土开裂前

混凝土开裂前，钢筋与混凝土界面间黏结应力较小。由于混凝土尚未开裂，厚壁圆筒全部处于线弹性阶段，可依据CEB-FIP Model Code1990[11]公式，建立应力τ和滑移s之间的关系

(10)

式中：τm为极限黏结应力。

当混凝土达到即将开裂的临界点时，即r=Rb处的拉应力达到混凝土抗拉强度时，可使用式(8)计算r=Rb时的黏结应力τb，此时式(8)中的Ri=Rb，再利用式(10)计算此时钢筋的滑移sb，即

(11)

式中：smax依据CEB-FIP Model Code1990[11]取值，当混凝土保护层厚度和钢筋直径比c/db≤1时，smax取0.6 mm；当c/db≥5时，smax取1 mm；当1≤c/db≤5时，采用线性插值计算smax。

2.2 混凝土开裂后

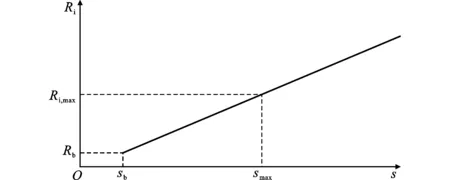
图9钢筋端部滑移与混凝土开裂半径关系Fig.9Relationship Between Slip at Steel Bar End and Radius of Cracked Concrete

混凝土开裂后，厚壁圆筒分为开裂内层和未开裂外层两部分，开裂半径Ri也从Rb向Rc增长。如图9所示，近似认为混凝土开裂半径Ri和端部滑移s之间存在线性关系[24-25]，由此推导得到Ri与s的关系式为

Ri=m(s-sb)+Rb

(12)

式中：m为斜率，依据文献[24]可取m=200/3。

将Ri代入式(8)，(9)中计算黏结应力τ，即可得到混凝土开裂后界面黏结应力-端部滑移关系。

3 模型验证

为检验上述理论分析模型的准确性，将已有高温后钢筋拉拔试验结果与模型预测结果进行比较。表1列出了所搜集的已有钢筋拉拔试验及参数，其中lb为锚固长度。

3.1 高温后钢筋-混凝土界面黏结强度对比

图10～12对比了高温后界面黏结强度的试验值和模型预测值，试验数据取自Haddad等[2]、Mor-ley等[3]、Hlavicka[4]、Yang等[6]、Bingol等[7]的钢筋拉拔试验，其中τb,T，τb,20 ℃分别为高温(r=Ri)和常温的黏结应力，*表示试件升温时未施加荷载，仅冷却后加载。图10中Morley等[3]的试验包括4组混凝土保护层厚度及2种加载方式，一为升温时施加3.7 MPa的荷载， 试件冷却后继续加载至试件破坏，二为升温时不施加荷载，仅在试件冷却后开始施加荷载直至试件破坏。图11中Bingol等[7]的试验包括2种不同的混凝土强度(C20和C35)、3种不同的钢筋锚固长度(lb=6,10,16 cm)、2种不同的冷却方式(自然冷却A和喷水冷却W)。图12对比了前述所有试验值与模型预测值，共计118组数据，模型预测值与试验值之比的均值为1.08，方差为0.127，可以看出模型预测界面黏结强度与试验值吻合较好，从而验证了理论分析模型的准确性。同时前述理论推导过程充分考虑了钢筋拉拔试件中各设计参数如钢筋尺寸、混凝土保护层厚度、混凝土强度、弹性模量以及断裂能对钢筋-混凝土界面黏结性能的影响，预测结果也表明该理论分析模型广泛适用于不同参数钢筋拉拔试验的高温后界面黏结强度的分析与预测。

3.2 界面黏结应力-端部滑移曲线对比

图13～15对高温后界面黏结应力-端部滑移关系的试验值和预测值进行比较。试验数据取自Haddad等[2]、Morley等[3]和Tang等[21]。Haddad等[2]试验采用100 mm×100 mm×200 mm棱柱体试件，钢筋直径为20 mm，黏结长度为150 mm，混凝土保护层厚度为40 mm，试件遭受350，500，600，700 ℃四个不同温度的损伤。Morley等[3]试验采用直径150 mm，长度300 mm的圆柱体拉拔试件，钢筋直径为16mm，黏结长度为2倍的钢筋直径，保护层厚度为55 mm，试件遭受200，250，400，565，720 ℃五个不同温度的损伤。Tang等[21]试验采用边长150 mm的正方体试件，钢筋直径为20 mm，黏结长度为100 mm，保护层厚度为65 mm，试件遭受300，400，500 ℃三个不同温度损伤。通过以上3组理论模型预测结果与试验结果的对比可以看出，总体上模型能够预测钢筋拉拔试件经受不同高温损伤后的界面黏结应力-端部滑移曲线。

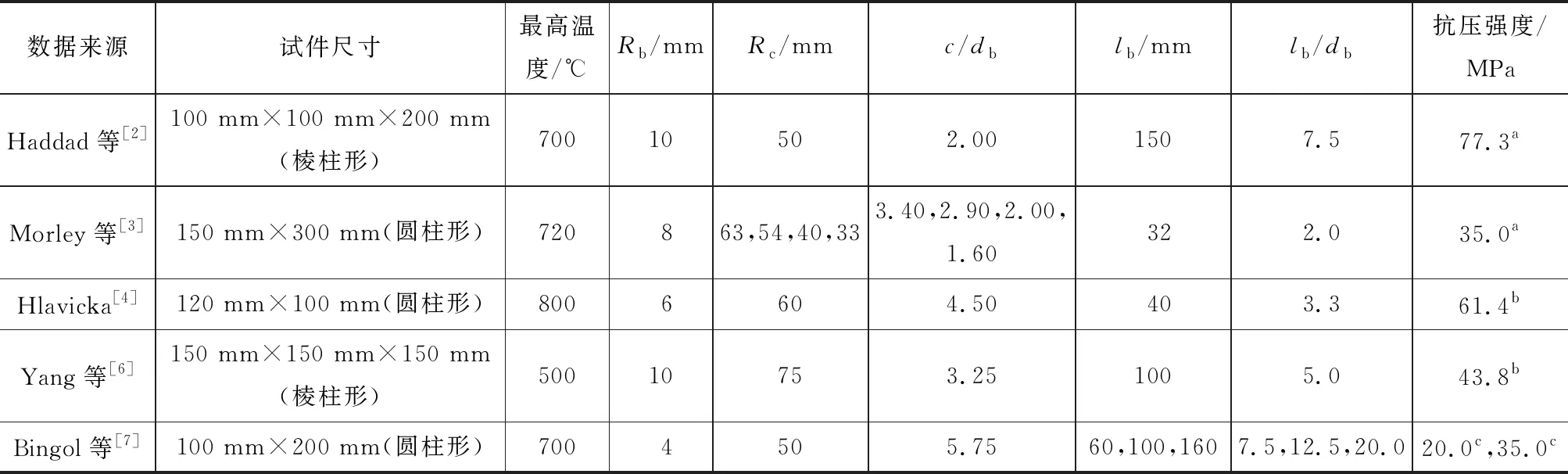
表1高温后钢筋拉拔试验及参数Tab.1Investigated Parameters of All the Pull-out Tests After Exposure to High Temperatures

图10Morley等[3]界面黏结强度试验结果与模型预测结果对比Fig.10Comparison Between Test Results from Morley et al[3] and Model Prediction Results of Interfacial Bond Strength

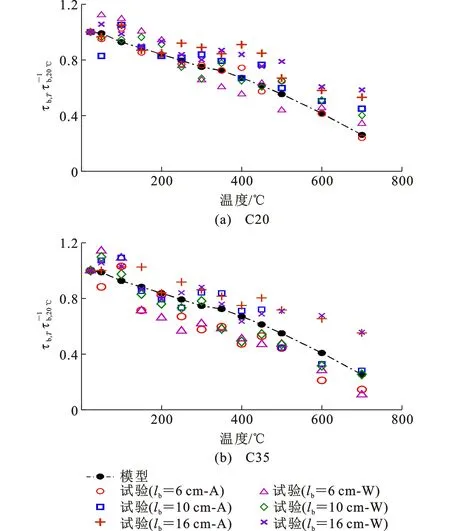
图11Bingol等[7]界面黏结强度试验结果与模型预测结果对比Fig.11Comparison Between Test Results from Bingol et al[7] and Model Prediction Results of Interfacial Bond Strength

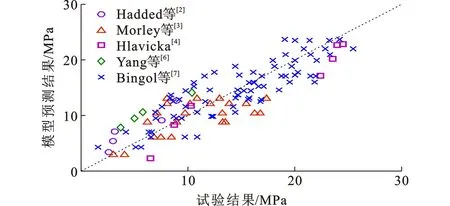
图12界面黏结强度试验结果与模型预测结果对比Fig.12Comparison Between Test Results and Model Prediction Resuts of Interfacial Bond Strength

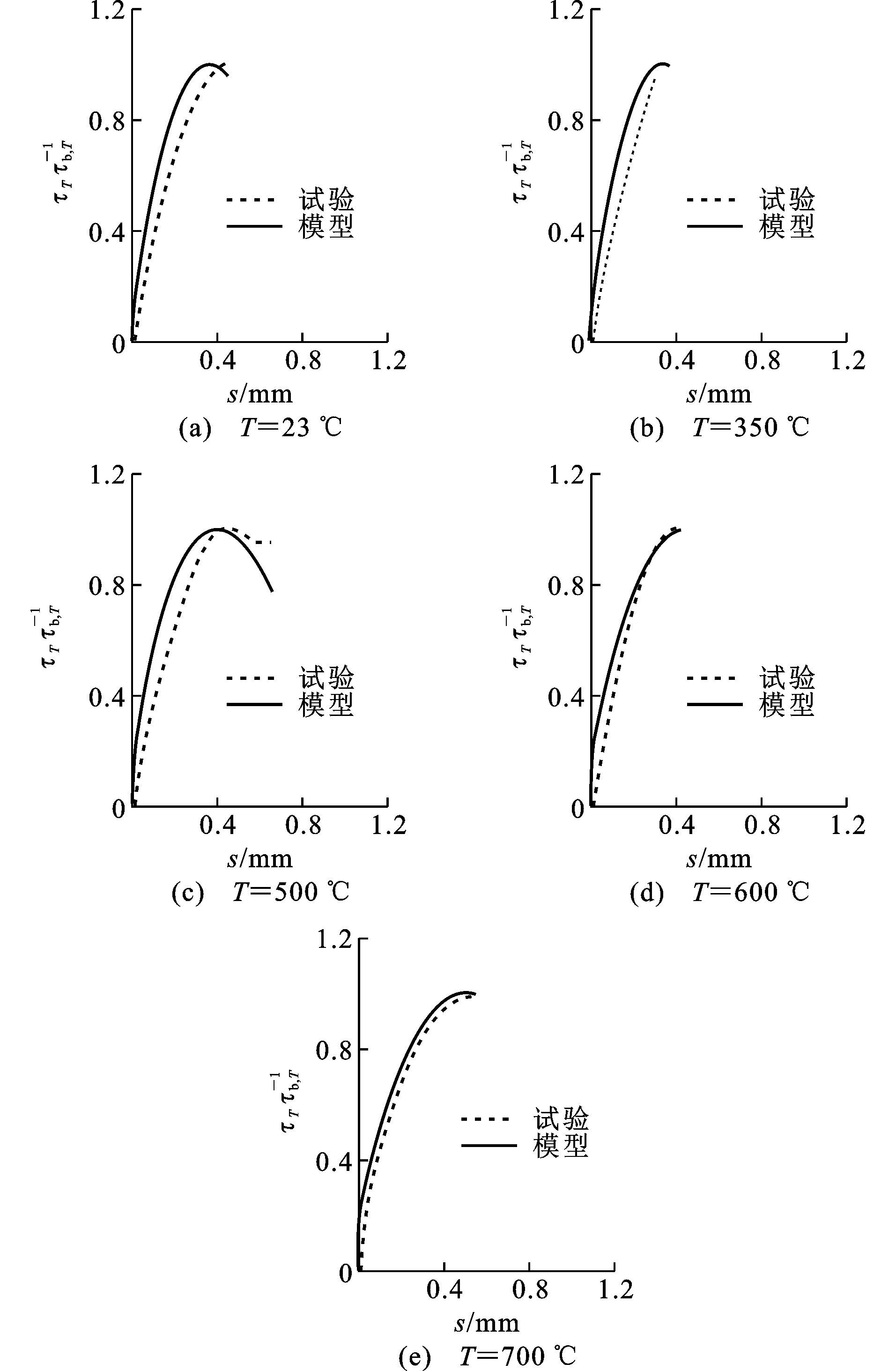
图13Haddad等[2]界面黏结应力-端部滑移曲线试验结果与模型预测结果对比Fig.13Comparison Between Test Results from Haddad et al[2] and Model Prediction Results of Interfacial Bond Stress-end Slip Curves

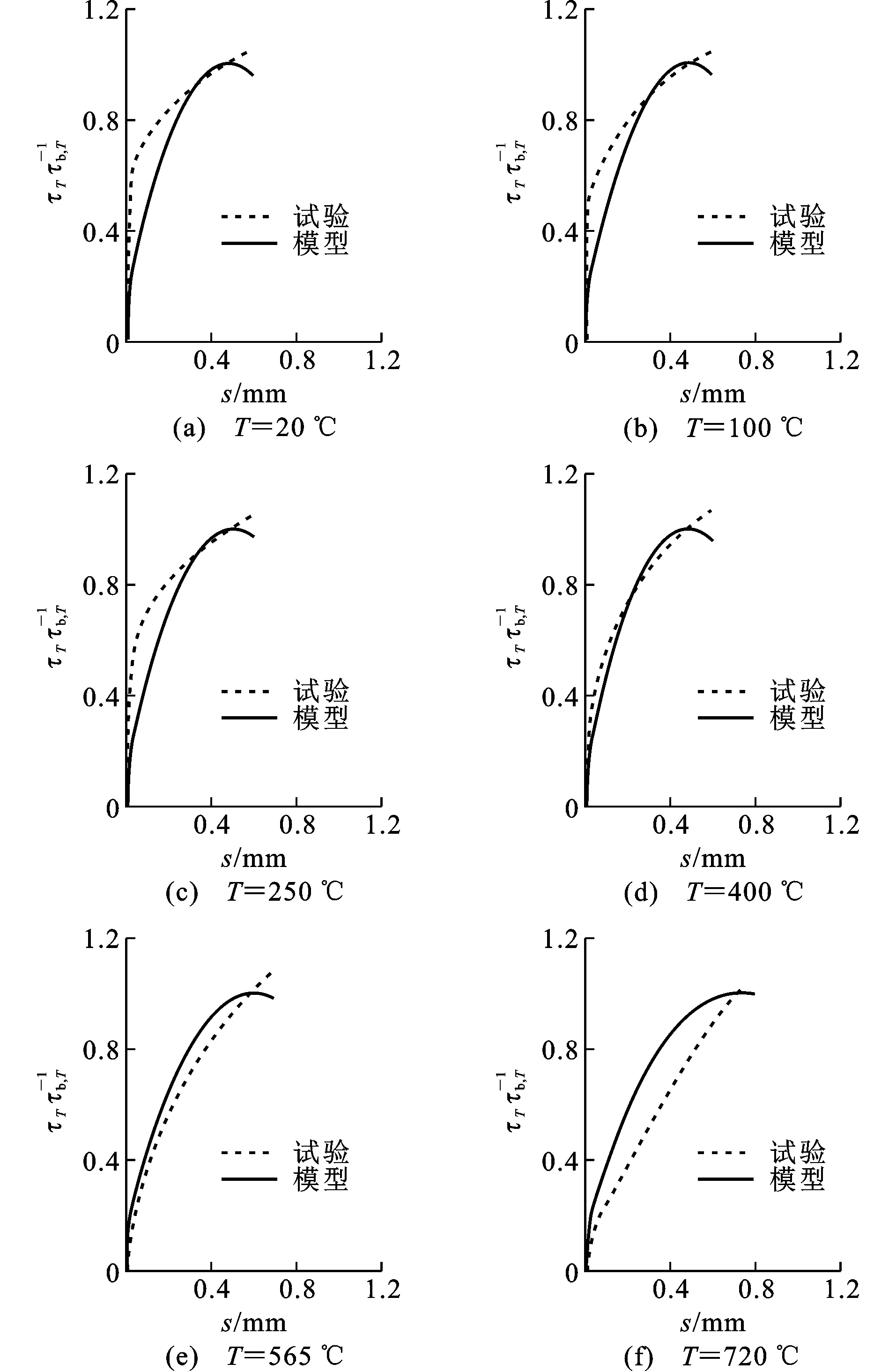
图14Morley等[3]试验界面黏结应力-滑移曲线对比Fig.14Comparison Between Test Results from Morley et al[3] and Model Prediction Results of Interfacial Bond Stress-end Slip Curves

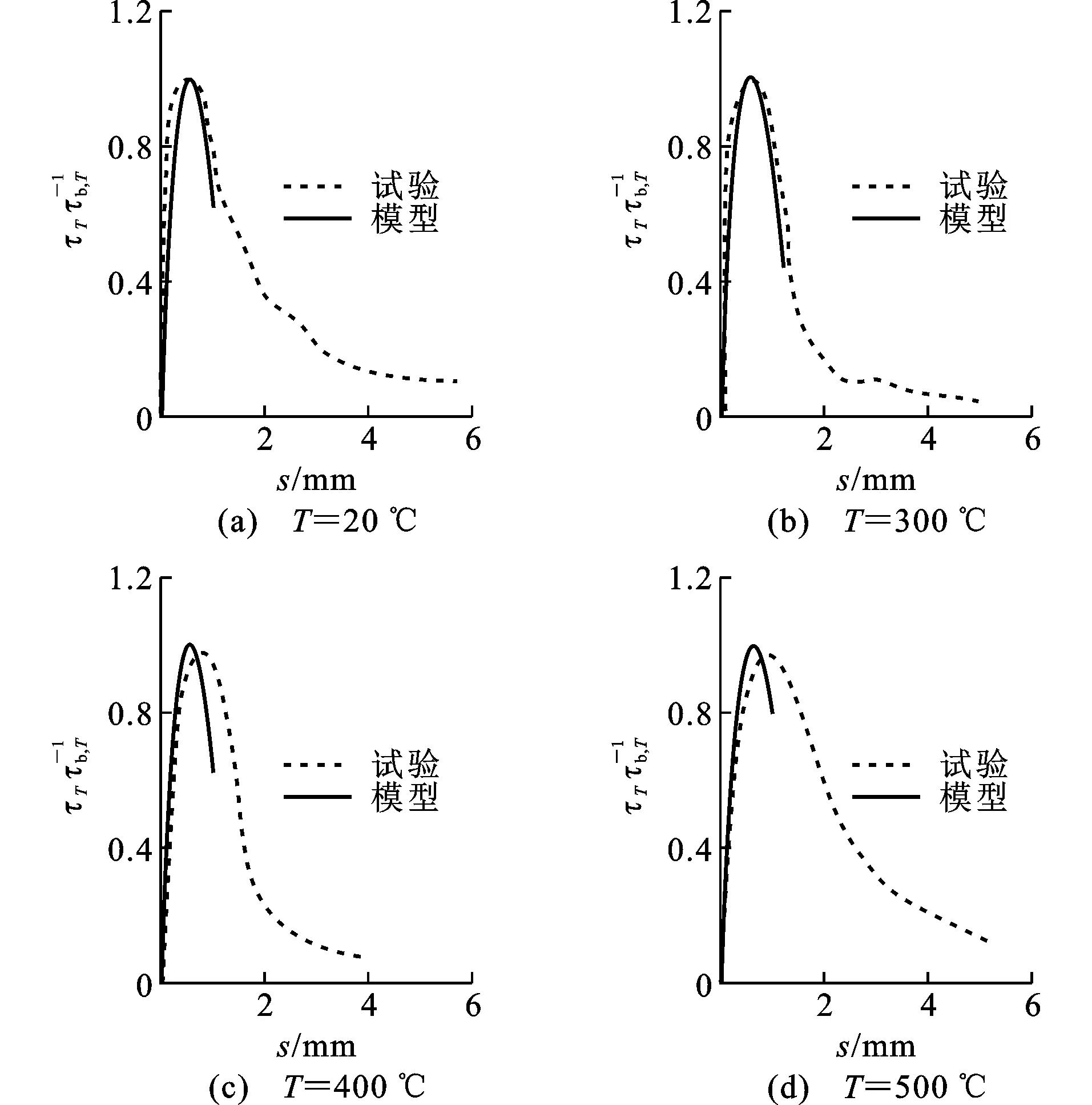
图15Yang等[6]试验界面黏结应力-滑移曲线对比Fig.15Comparison Between Test Results from Yang et al[6] and Model Prediction Results of Interfacial Bond Stress-end Slip Curves

4 结语

本文对高温后钢筋-混凝土界面黏结性能进行理论分析，建立了高温后界面黏结强度模型和界面黏结应力-端部滑移关系。该理论模型以变形钢筋的拉拔试件为研究对象，将包裹变形钢筋的混凝土保护层简化为受到均匀内压力的厚壁圆筒。此圆筒分为开裂内层和未开裂外层两部分，对开裂内层基于混凝土抗拉软化模型，考虑高温后混凝土抗拉强度、弹性模量及断裂能的材性劣化，推导出高温后界面黏结强度模型。通过引入端部滑移与内层开裂混凝土半径间的线性关系，建立了高温后界面黏结应力-端部滑移关系。理论分析过程中，充分考虑了钢筋拉拔试件各设计参数如钢筋尺寸、混凝土保护层厚度、混凝土抗压强度、抗拉强度、弹性模量以及断裂能对钢筋-混凝土界面黏结性能的影响，同时准确表征了高温后混凝土材料性能的劣化。通过与前人拉拔试验结果进行对比分析，验证了本文理论分析模型的准确性。需要说明的是，由于本文中考虑的高温后钢筋、混凝土材性为普通钢筋混凝土结构，因此所建立的高温后界面黏结强度模型和界面黏结应力-端部滑移关系适用于普通钢筋混凝土结构，但是本文的理论分析方法同样适合于所有的混凝土类型和钢筋类型。