一类带记忆项的非经典热方程的爆破问题
2021-01-16吴少华吴迎东
吴少华,吴迎东,程 新
(武汉大学数学与统计学院,湖北 武汉 430072)
1 引言
在本文中,我们考虑如下模型:
在过去几十年中,抛物型方程的研究取得了丰硕的成果,其中以美国科学院院士Avner Friedman为首的数学家,更是将这一领域的研究推向了极高的水平.在文献[1]中,Friedman院士利用先验估计证明了抛物组解的可微性,随后,他在文献[2]中证明了,各种不同的积分增长条件下,一般抛物组的唯一性定理.Mizohata[3]则用半群的方法给出了Cauchy问题的存在性,Tychonov[4]则对热传导方程首先建立了Cauchy问题解的唯一性.在Friedman的论文[5-8]中,集中解决了关于抛物型方程的自由边界问题,即
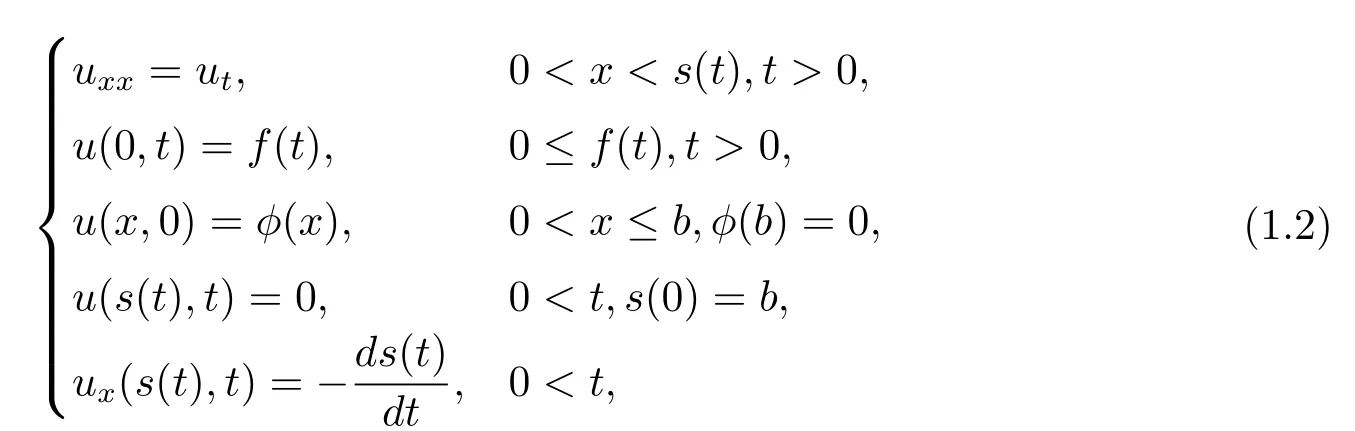
其中x=s(t)不是已经给定的边界,而是和u(x,t)一起寻找的自由边界.在此基础上,自由边界的问题得到较为充分的研究,Douglas[9]与Kyner[10]则发展了Friedman研究自由边界的方法,考虑了非经典的热方程.
近年来,学者们则开始研究关于热传导方程带记忆项边界问题的研究[11,12],记忆项即带有时间积分边界条件.带记忆项的自由边界问题,有核反应堆动力学相关问题[13],人口流动问题[14].关于这类模型的局部(或整体)解的存在性,稳定性,有限时间爆破都被Y.Yamada,P.Souplet和P.Vernole等人讨论清楚了.
粘弹性模型中也研究了扩散中的记忆项非牛顿流体中的力[15],还有涉及带有记忆项的Fisher方程形式的模型的研究[16,17].在这里需要指出的是,分数阶时间导数作为记忆算子已经在D’Arcy定律和分子传输的记忆形式学中进行了研究[18],关于气候模型中扩散和反应,我们也引入了记忆条件[19].
有两个原因,促使我们研究问题(1.1).第一,在文献[20]中,模型(1.3)
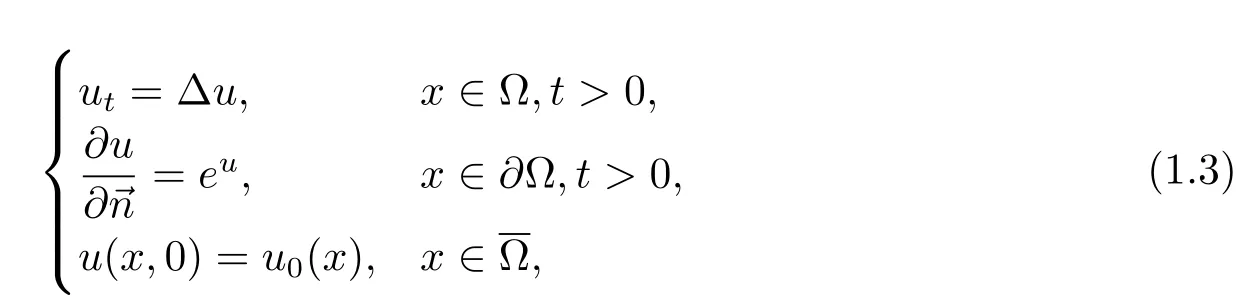
已经被证明,所有非负解都会在有限时间爆破,爆破只会发生在边界.
第二,在文献[11]中,邓铿研究了带记忆边界条件的热方程(1.4),证明了解的全局存在性与爆破性质.
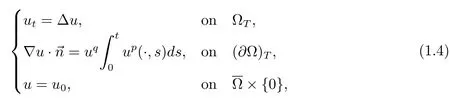
式子中,p≥0,q≥0,and ΩT=Ω×(0,T),其中Ω是上的有界区域,具有光滑的边界∂Ω,是单位法向量,指向向外.初始值u0是一个在上非负连续的函数.他的主要结论是:如果0≤p+q≤1,则(1.4)的解是全局的.另一方面,如果p+q>1,则所有非负,平凡的解是在有限时间爆破的.
2 解的最值性质
在这一节,我们将证明一个定理,它将辅助证明定理4.1,这个定理刻画的是解的最大值属性,证明主要通过构造两个函数.
定理2.1如果u(x,t)是×(0,T)(T<1)上的连续函数,满足
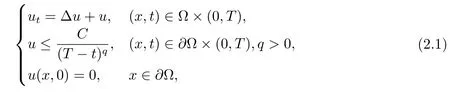
则对任意的Ω′⊂⊂Ω,我们有sup{u(x,t);(x,t)∈Ω′×(0,T)}<∞.
证不失一般性,我们认为∂Ω是光滑的,且是C2的.

3 有限时间爆破
下面,我们通过格林函数方法构造一个关于v(x,t)的表达式,然后利用Banach不动点定理,我们可以证明该表达式是问题(1.1)的局部经典解.
定理3.2设GN(x,y,t,τ)是表示带有齐次Neumann边界条件的热方程的格林函数,则在问题(1.1)的条件下我们有:
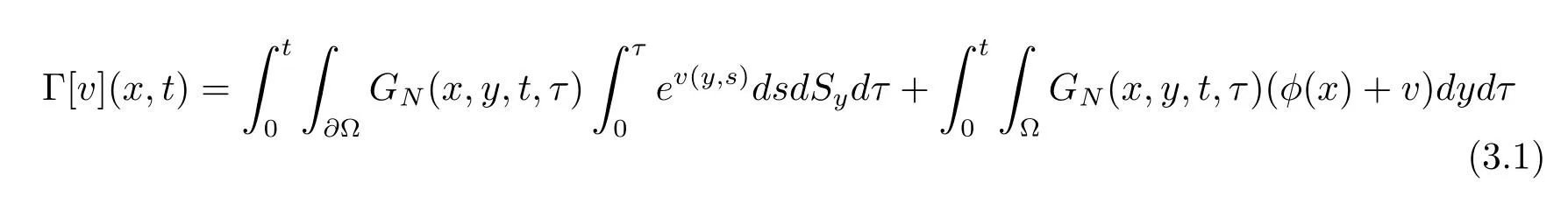
对较小的t是一个压缩映射.
证根据文献[21],令
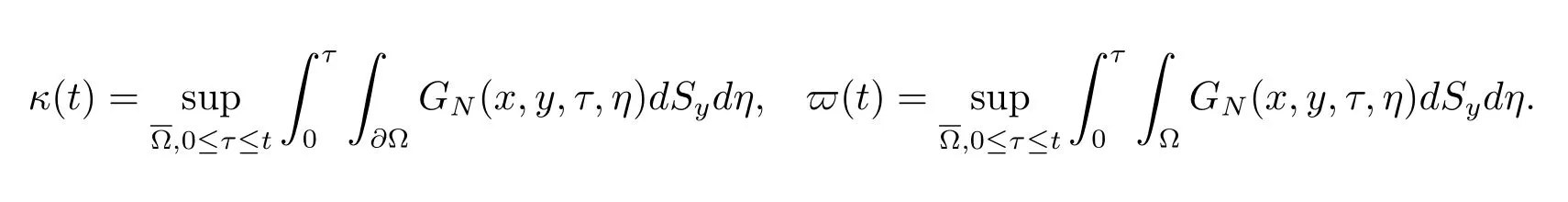

定理3.3问题(1.1)的非负,非平凡解在有限时间内爆破.
证后文中,在不引起任何混淆的情况下.我们使用ci或Ci(i=0,1,2,...)表示各种正常数.如文献[22]中所示,我们有
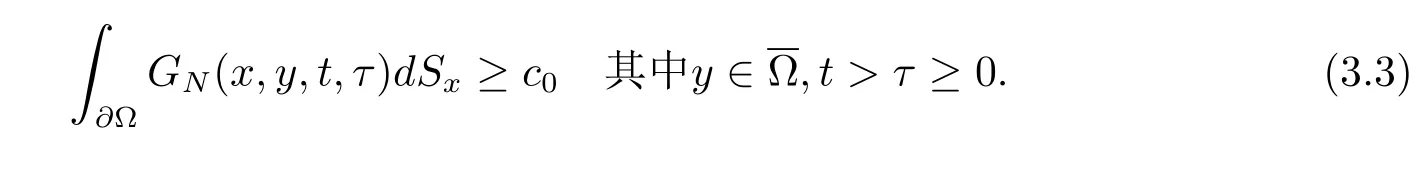
根据(3.2),(3.3)和詹森不等式得到
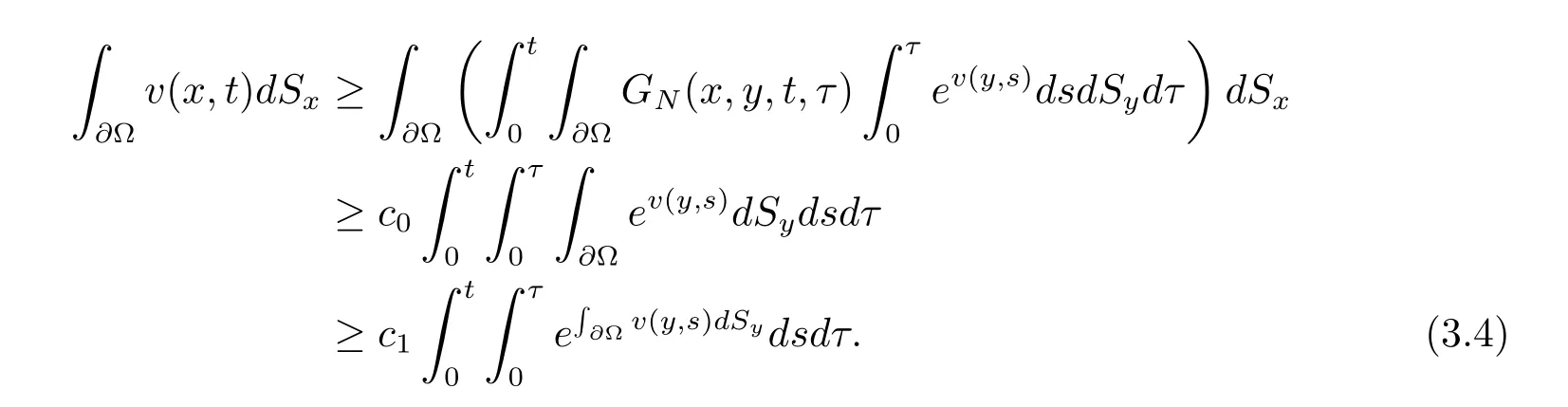
另一方面,根据(3.2),(3.3),我们有

显然,k(t) 满足
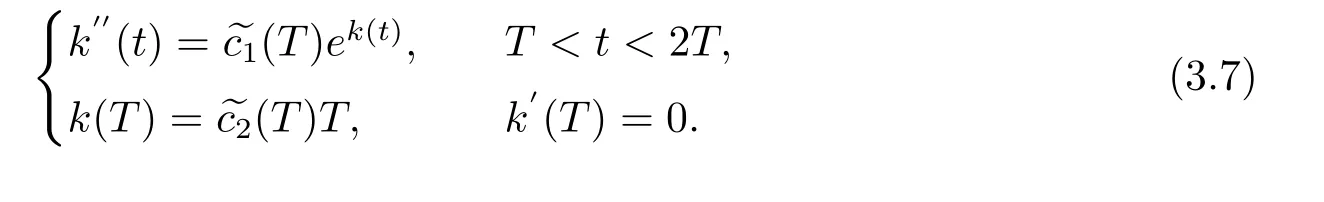
将(3.7)中的方程乘以k′(t)并从T到t积分,我们得到

对于足够大的T,不等式(3.8)产生矛盾.
4 边界爆破

将上式在(t,T)上积分,得到
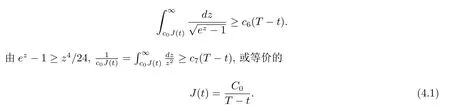
取 Ω′⊂⊂Ω,满足d(∂Ω,Ω′)=∊>0,对于这样的 Ω′,我们再取 Ω′′⊂⊂Ω,满足 Ω′⊂⊂Ω′′,d(∂Ω′′,Ω′)≥∊/3,d(∂Ω,Ω′)≥∊/3,对∀∊>0,下式成立
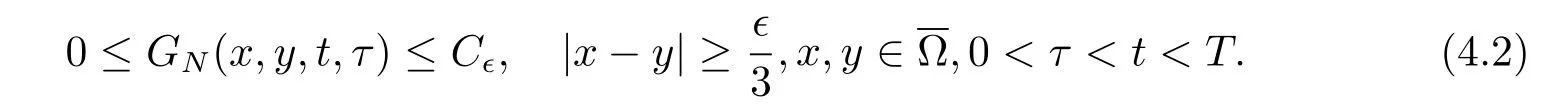
根据(3.2),(4.1),(4.2)得到
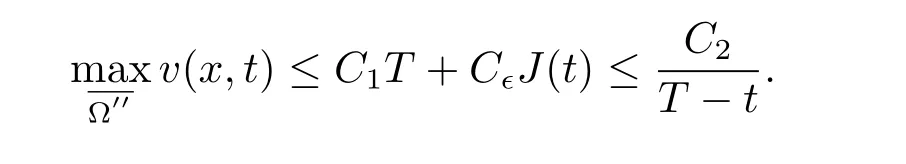
根据定理2.1,我们得到

对于某些C4>0,我们的ψ ∈C2(Ω′′) 满足
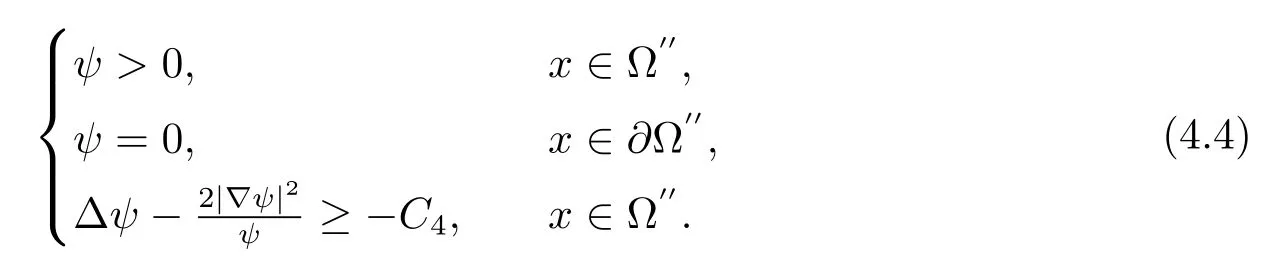
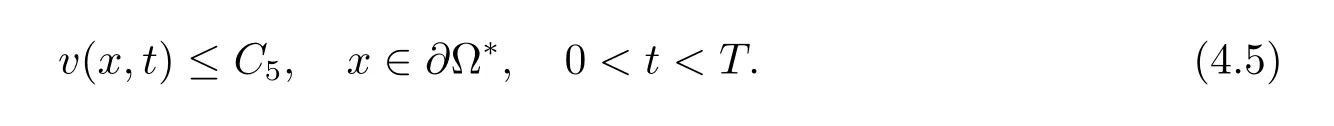
猜你喜欢
杂志排行
数学杂志的其它文章
- ANNOUNCEMENT ON“MAXIMUM PRINCIPLE FOR NON-UNIFORMLY PARABOLIC EQUATIONS AND APPLICATIONS”
- ANNOUNCEMENT ON“SHARP ERROR ESTIMATE OF BDF2 SCHEME WITH VARIABLE TIME STEPS FOR LINEAR REACTION-DIFFUSION EQUATIONS”
- ON THE CHARACTERIZATION OF COMPACTNESS IN THE SPACE OF HENSTOCK-KURZWEIL INTEGRABLE FUNCTIONS
- COMMON COUPLED FIXED POINT THEOREMS FOR CONTRACTIVE MAPPINGS OF MANY VARIABLES IN FUZZY METRIC SPACES
- K-ORDER GENERALIZED DERIVATIONS OF WEIGHT λ ON δ JORDAN-LIE TRIPLE SYSTEMS
- GRADIENT ESTIMATE FOR POSITIVE SOLUTIONS OF THE PME UNDER GEOMETRIC FLOW
