ANNOUNCEMENT ON“MAXIMUM PRINCIPLE FOR NON-UNIFORMLY PARABOLIC EQUATIONS AND APPLICATIONS”
2021-01-16ZHANGXicheng
ZHANG Xi-cheng
(School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)
Abstract:In this note we announce the global boundedness for the solutions to a class of possibly degenerate parabolic equations by De-Giorgi’s iteration.In particular,the existence of weak solutions for possibly degenerate stochastic differential equations with singular diffusion coefficients is obtained.
Keywords: maximum principle;De-Giorgi’s iteration;stochastic differential equation;Krylov’s estimate
Consider the following elliptic equation of divergence form in(d≥2):

wherea:→is a Borel measurable function and∇:=(∂x1,···,∂xd).Whenais uniformly elliptic,the celebrated works of De-Giorgi[1]and Nash[2]said that any weak solutions of elliptic equation(1)are bounded and H¨older continuous.Moreover,Moser[3]showed that any weak solutions of(1)satisfy the Harnack inequality.In[4],Trudinger considered the non-uniformly elliptic equation(1)under the following integrability assumptions:

where
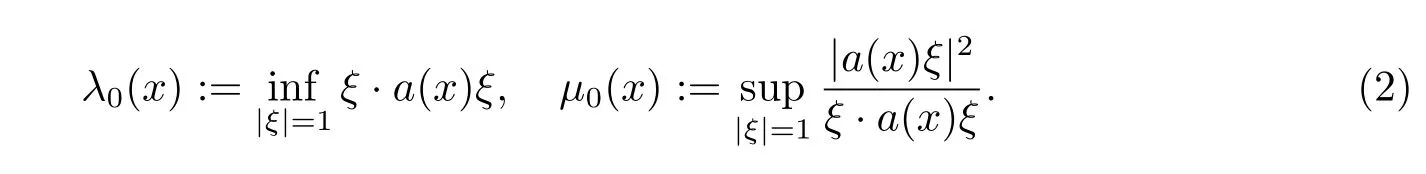
He showed that any generalized solutions of(1)are locally bounded and weak Harnack inequality holds.Recently,Bella and Sch¨affner[5]showed the same results under the followingsharpcondition onp0,p1,
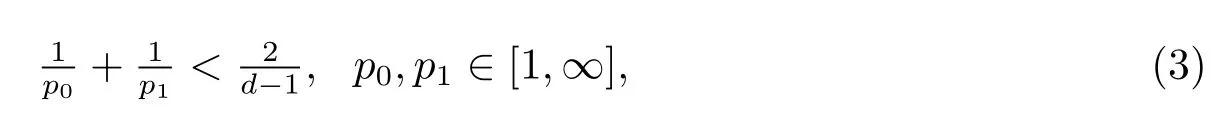
Here we extend the main result of[5]to parabolic case.More precisely,we consider the following parabolic equation of divergence form in:

where

are Borel measurable functions.As in(2),we introduce

and suppose thatλandµare nonnegative Borel measurable functions.
Definition 0.1A continuous functionu:→is called a Lipschitz weak(super/sub)-solution of PDE(4)if∇uis locally bounded and for any nonnegative Lipschitz functionϕonwith compact support,


For simplicity of notations,we introduce the following parameter set
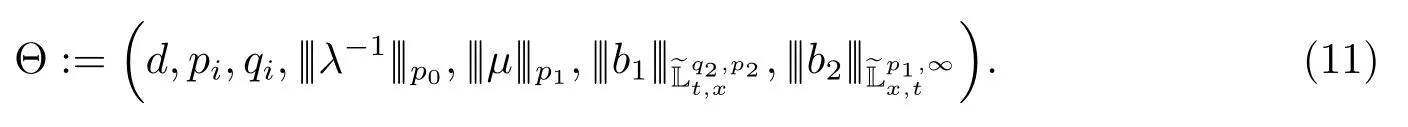
We have the following apriori estimate.

Consider the following heat equation with divergence free driftb:


whereWis ad-dimensional standard Brownian motion.We recall the following notion of weak solutions to SDE(15).


Note that the starting point can be zero and the uniqueness follows from[8].
Example 0.8The following two dimensional degenerate SDE admits a solution:
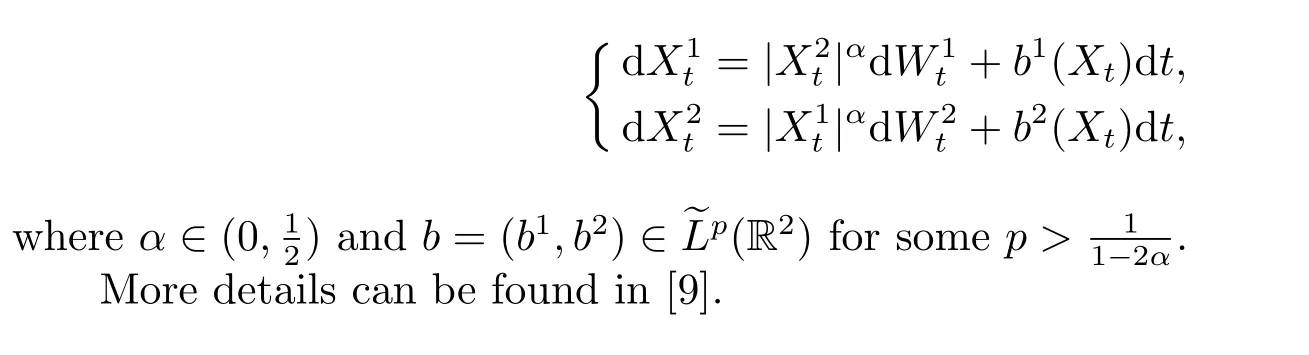
杂志排行
数学杂志的其它文章
- ANNOUNCEMENT ON“SHARP ERROR ESTIMATE OF BDF2 SCHEME WITH VARIABLE TIME STEPS FOR LINEAR REACTION-DIFFUSION EQUATIONS”
- ON THE CHARACTERIZATION OF COMPACTNESS IN THE SPACE OF HENSTOCK-KURZWEIL INTEGRABLE FUNCTIONS
- COMMON COUPLED FIXED POINT THEOREMS FOR CONTRACTIVE MAPPINGS OF MANY VARIABLES IN FUZZY METRIC SPACES
- K-ORDER GENERALIZED DERIVATIONS OF WEIGHT λ ON δ JORDAN-LIE TRIPLE SYSTEMS
- GRADIENT ESTIMATE FOR POSITIVE SOLUTIONS OF THE PME UNDER GEOMETRIC FLOW
- 一类带记忆项的非经典热方程的爆破问题
