COMMON COUPLED FIXED POINT THEOREMS FOR CONTRACTIVE MAPPINGS OF MANY VARIABLES IN FUZZY METRIC SPACES
2021-01-16WANGShiboHUXinqi
WANG Shi-bo,HU Xin-qi
(School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)
Abstract:In this paper,we propose a notion of coincidence point between mappings in any number of variables.The main results of this paper are generalizations of the main results of fixed point theorems in partially ordered fuzzy metric spaces from low dimension to high dimension.
Keywords: fixed point theorem;metric space;fuzzy metric space;partially ordered set;compatible mapping
1 Introduction
Since Zadeh[1]introduced the concept of fuzzy sets,many authors have extensively developed the theory of fuzzy sets and applications.George and Veeramani[2,3]gave the concept of fuzzy metric space and defined a Hausdorfftopology on this fuzzy metric space which have very important applications in quantum particle physics particularly in connection with both string and E-infinity theory.
The notion of coupled fixed points was introduced by Guo and Lakshmikantham[4]in 1987.In a recent paper,Gnana-Bhaskar and Lakshmikantham[5]introduced the concept of mixed monotone property for contractive operators of the formF:X×X→X,whereXis a partially ordered metric space,and the established some coupled fixed point theorems.Lakshmikantham and´Ciri´c[6]discussed the mixed monotone mappings and gave some coupled fixed point theorems which can be used to discuss the existence and uniqueness of solution for a periodic boundary value problem.
Shaban Sedghi et al[7]gave a coupled fixed point theorem for contractions in fuzzy metric spaces,and Jin-xuan Fang[8]gave some common fixed point theorems underφcontractions for compatible and weakly compatible mappings in Menger probabilistic metric spaces.Xin-Qi Hu[9]proved a common fixed point theorem for mappings underϕcontractive conditions in fuzzy metric spaces.B.S.Choudury et.al.[10]established coupled coincidence point and coupled fixed point results for compatible mappings in partially ordered fuzzy metric spaces and gave an example to illustrate the main theorems.In 2015,Jinxuan-Fang[11]generlized a crucial fixed point theorem for probabilisticϕ-contraction on complete Menger space.Other more works on this topic can be found in[12-23].
Now we propose a notion of coincidence point between mappings cases of these results that are already known under some contractive conditions.
2 Mathematical Preliminaries
First we give some definitions.
Definition 2.1(see[2])A binary operation∗:[0,1]×[0,1]→[0,1]is continuoust-norm if∗satisfies the following conditions:
(1)∗is commutative and associative;
(2)∗is continuous;
(3)a∗1=afor alla∈[0,1];
(4)a∗b≤c∗dwhenevera≤candb≤dfor alla,b,c,d∈[0,1].
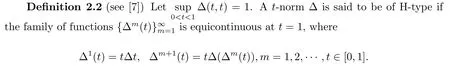
Thet−norm ∆M=min is an example oft-norm of H-type,but there are some othert-norms∆of H-type.
Obviously,∆ is a H-typetnorm if and only if for anyλ∈(0,1),there existsδ(λ)∈(0,1)such that∆m(t)>1−λfor allm∈N,whent>1−δ.
Definition 2.3(see[2])A 3-tuple(X,M,∗)is said to be a fuzzy metric space ifXis an arbitrary nonempty set,∗is a continuoust-norm andMis a fuzzy set onX2×(0,+∞)satisfying the following conditions,for eachx,y,z∈Xandt,s>0,
(FM-1)M(x,y,t)>0;
(FM-2)M(x,y,t)=1 if and only ifx=y;
(FM-3)M(x,y,t)=M(y,x,t);
(FM-4)M(x,y,t)∗M(y,z,s)≤M(x,z,t+s);
(FM-5)M(x,y,·):(0,∞)→[0,1]is continuous.
Let(X,M,∗)be a fuzzy metric space.Fort>0,the open ballB(x,r,t)with a centerx∈Xand a radius 0
A subsetA⊂Xis called open if for eachx∈A,there existt>0 and 0 Example 2.4Let(X,d)be a metric space.De finet-norma∗b=aband for allx,y∈Xandt>0,M(x,y,t)=.Then(X,M,∗)is a fuzzy metric space.We call this fuzzy metricMinduced by the metricdthe standard fuzzy metric. Letnbe a positive integer.Xwill benote a non-empty set andXndenote the product spaceXn= Definition 2.5(see[6])LetXbe a non-empty set,F:X→Xandg:X→Xbe two mappings.We sayFandgare commutative(or thatFandgcommute)ifgFx=Fgxfor allx∈X. Definition 2.6(see[6])The mappingsFandgwhereF:X→Xandg:X→X,are said to be compatible if limn→∞d(Fgxn,gFxn)=0 whenever{xn}is a sequence inX,such that limn→∞F(xn)=limn→∞g(xn)=xfor allx∈Xare satisfied. Definition 2.7(see[6])Two mappingsFandgon a metric space(X,d)are said to be weakly compatible if they commute at their coincidence points,that is,ifFx=gxfor somex∈X,thenFgx=gFx. Let Λn={1,2,···,n},A,Bsatisfy thatA∪B= ΛnandA∩B=∅.We will denoteΩA,B={σ:Λn→Λn,σ(A)⊆Aandσ(B)⊆B},and={σ:Λn→Λn,σ(A)⊆Bandσ(B)⊆A}. Let(X,≤)be a partially ordered space,x,y∈Xandi∈Λn.We use the following notation Letσ1,σ2,···,σn,τ: Λn→Λnben+1 mappings and let Φ be the(n+1)-tuple(σ1,σ2,···,σn,τ). Definition 2.8(see[13])LetF:Xn→X,g:X→X.A point(x1,x2,···,xn)∈Xnis called a Φ-coincidence point of the mappingsFandgif Ifgis the identity mapping onX,then(x1,x2,···,xn)∈Xnis called a Φ- fixed point of the mappingF. Definition 2.9Let(X,≤)be a partially ordered space.We say thatFhas the mixedg-monotone property ifFisg-monotone non-decreasing in argument ofAandg-monotone non-increasing in argument ofB,i.e.,for allx1,x2,···,xn,y,z∈Xand alli, It is obvious that the above formula is equivalent to the following: Definition 2.10LetF:Xn→Xandg:X→X.Fandgare called weakly compatible mappings if forx1,x2,···,xn,it satisfies it implies Lemma 3.1(see[23])Forn∈N,letgn:(0,+∞)→(0,+∞)andFn:R→[0,1].Assume that sup{F(t):t>0}=1 and for anyt>0, If eachFnis nondecreasing,then limn→+∞Fn(t)=1 for anyt>0. Theorem 3.2(see[21])Let(X,M,∆)be a complete fuzzy metric space with ∆ a triangular norm of H-type.Letϕ∈Ψω,where Ψωis denoted as the class of all functionϕ:[0,+∞)→[0,+∞)such that for eacht>0 there exists anrt≥tsatisfying limn→+∞ϕn(rt)=0.LetT:X→Xbe a mapping,M(Tx,Ty,ϕ(t))≥M(x,y,t)for allx,y∈Xand allt>0.ThenThas a unique fixed pointx∗.In fact,for anyx0∈X,limn→+∞Tnx0=x∗. ProofΨ is denoted as the class of all functionϕ:[0,+∞)→[0,+∞)be continuous withϕ(t) By Lemma 3.1,we have Now letn∈Nandt>0,we show by induction that,for anyk∈, This is obvious fork=0.Assume it holds for somek,by the monotonicity of∆,we have which completes the induction.By∆n(1)=1 and∆is a triangular norm of H-type,for anyt>0 andε>0,there isδ>0 such that ifs∈(1− δ,1],then ∆n(s)>1− εfor alln∈N. Letϕ∈Ψω.PutA={t>0:limn→+∞ϕn(t)=0},ift∈A,we denote byktthe first integer number such that Ift∈[0,+∞)A,take anrt>tsuch thatrt∈A,and,again,denote byktthe first integer number such that Now define a functionψ:[0,+∞)→[0,+∞)as follows: It is proved thatψ∈Ψ(see[21]).Hence we can applyψand get theorem 3.3 proved by the condition thatϕ∈Ψω. Theorem 3.4Let(X,M,∆,≤)be a complete ordered fuzzy metric space with ∆ a triangular norm of H-type.Let Φ =(σ1,σ2,···,σn,τ)be(n+1)-tuple of mappings from Λninto itself such thatτ∈ΩA,Bis a permutation and verifying thatσi∈ΩA,Bifi∈Aandσi∈ifi∈B.Letϕ:[0,+∞)→[0,+∞),ϕ ∈Ψω,F:Xn→Xandg:X→Xbe two mappings,F(Xn)⊆g(X),Fis continuous and has the mixedg-monotone property,Fandgare weakly compatible mappings and ProofLetY=Xn.For(x1,x2,···,xn),(y1,y2,···,yn)∈Xn,t>0,M∗and binary relationonYare defined as It is easy to verify that(Y,)is a partially ordered set and(Y,M∗,∆)is a complete fuzzy metric space.Then(Y,M∗,∆,)is a complete ordered fuzzy metric space. For(x1,x2,···,xn)∈Y,:Y→Y,:Y→Yare defined as which implies that Fori∈A,ifj∈A,then there existsk∈Asuch thatσi(j)=τ(k);ifj∈B,then there existsk∈Bsuch thatσi(j)=τ(k).So,we have That is That is, Continuing in this way,we can get Similarly,fori∈B,we can have and Then that is, Following all the conditions of Theorem 3.3 and the proof,we can haveFandg,at least,one Φ-coincidence point. It is obvious that,ifFandgare compatible,then they are weakly compatible.So,we have the following theorem. Theorem 3.5Let(X,M,∆,≤)be a complete ordered fuzzy metric space with ∆ a triangular norm of H-type.Let Φ =(σ1,σ2,···,σn,τ)be(n+1)-tuple of mappings from Λninto itself such thatτ∈ΩA,Bis a permutation and verifying thatσi∈ΩA,Bifi∈Aandσi∈ifi∈B.Letϕ:[0,+∞)→[0,+∞),ϕ ∈Ψω,F:Xn→Xandg:X→Xbe two mappings,F(Xn)⊆g(X),Fis continuous and has the mixedg-monotone property,Fandgare compatible mappings and Corollary 3.6Let(X,M,∆,≤)be a complete ordered fuzzy metric space with ∆ a triangular norm of H-type.ϕ:[0,+∞)→[0,+∞),ϕ∈Ψω,LetF:X2→Xandg:X→Xbe two mappings,F(X2)⊆g(X),Fis continuous and has the mixedg-monotone property,Fandgbe weakly compatible mapping and Similarly,in Theorem 3.5,letn=3,we have Λ3={1,2,3},A={1,3},B={2}.σ1,σ3∈ΩA,Bandσ2∈,thenσ1(1)={1},σ1(2)={2},σ1(3)={3},σ2(1)={2},σ2(2)={1},σ2(3)={2}andσ3(1)={3},σ3(2)={2},σ3(3)={1}.Then we have the following corollary. Corollary 3.7Let(X,M,∆,≤)be a complete ordered fuzzy metric space with ∆ a triangular norm of H-type.ϕ:[0,+∞)→[0,+∞),ϕ∈Ψω,LetF:X3→Xandg:X→Xbe two mappings,F(X3)⊆g(X),Fis continuous and has the mixedg-monotone property,Fandgbe weakly compatible mapping and RemarkWhenFandgare commutative,they are weakly compatible,so we have the following theorem. Theorem 3.8Let(X,M,∆,≤)be a complete ordered fuzzy metric space with ∆ a triangular norm of H-type.Let Φ =(σ1,σ2,···,σn,τ)be(n+1)-tuple of mappings from Λninto itself such thatτ∈ΩA,Bis a permutation and verifying thatσi∈ΩA,Bifi∈Aandσi∈ifi∈B.Letϕ:[0,+∞)→[0,+∞),ϕ ∈Ψω,F:Xn→Xandg:X→Xbe two mappings,F(Xn)⊆g(X),Fis continuous and has the mixedg-monotone property,Fandgare commutative,and RemarkLetk∈[0,1),takingϕ(t)=ktin Theorem 3.4,3.5,3.8,we obtain the following corollaries. Corollary 3.9Let(X,M,∆,≤)be a complete ordered fuzzy metric space with ∆ a triangular norm of H-type.Let Φ =(σ1,σ2,···,σn,τ)be(n+1)-tuple of mappings from Λninto itself such thatτ∈ΩA,Bis a permutation and verifying thatσi∈ΩA,Bifi∈Aandσi∈ifi∈B.Letϕ:[0,+∞)→[0,+∞),ϕ ∈Ψω,LetF:Xn→Xandg:X→Xbe two mappings,F(Xn)⊆g(X),Fis continuous and has the mixedg-monotone property,Fandgare weakly compatible mappings and Corollary 3.10Let(X,M,∆,≤)be a complete ordered fuzzy metric space with ∆a triangular norm of H-type.Let Φ =(σ1,σ2,···,σn,τ)be(n+1)-tuple of mappings from Λninto itself such thatτ∈ΩA,Bis a permutation and verifying thatσi∈ΩA,Bifi∈Aandσi∈ifi∈B.Letϕ:[0,+∞)→[0,+∞),ϕ ∈Ψω,LetF:Xn→Xandg:X→Xbe two mappings,F(Xn)⊆g(X),Fis continuous and has the mixedg-monotone property,Fandgare compatible mappings and Corollary 3.11Let(X,M,∆,≤)be a complete ordered fuzzy metric space with ∆a triangular norm of H-type.Let Φ =(σ1,σ2,···,σn,τ)be(n+1)-tuple of mappings from Λninto itself such thatτ∈ΩA,Bis a permutation and verifying thatσi∈ΩA,Bifi∈Aandσi∈ifi∈B.Letϕ:[0,+∞)→[0,+∞),ϕ ∈Ψω,F:Xn→Xandg:X→Xbe two mappings,F(Xn)⊆g(X),Fis continuous and has the mixedg-monotone property,Fandgare commutative,and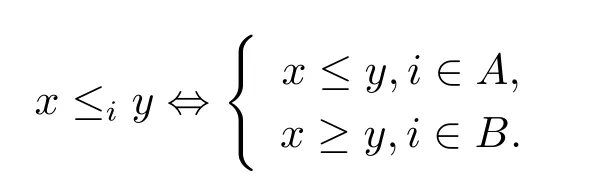
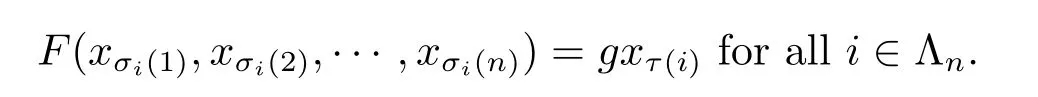


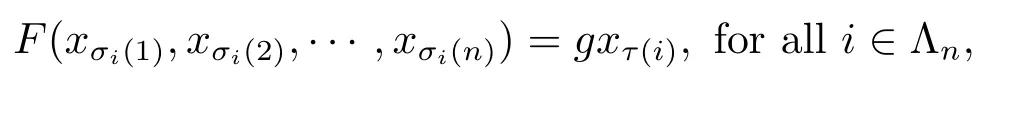

3 Main Results



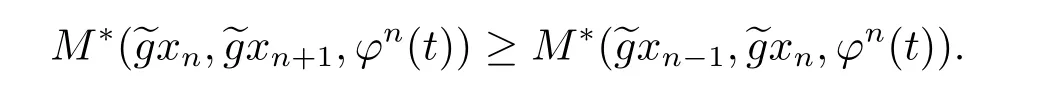
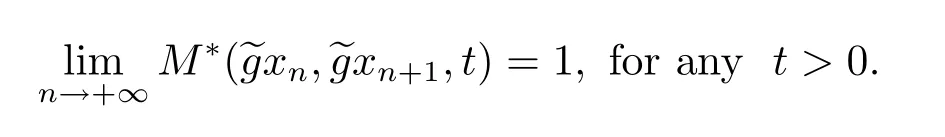
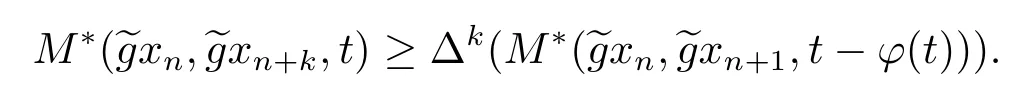
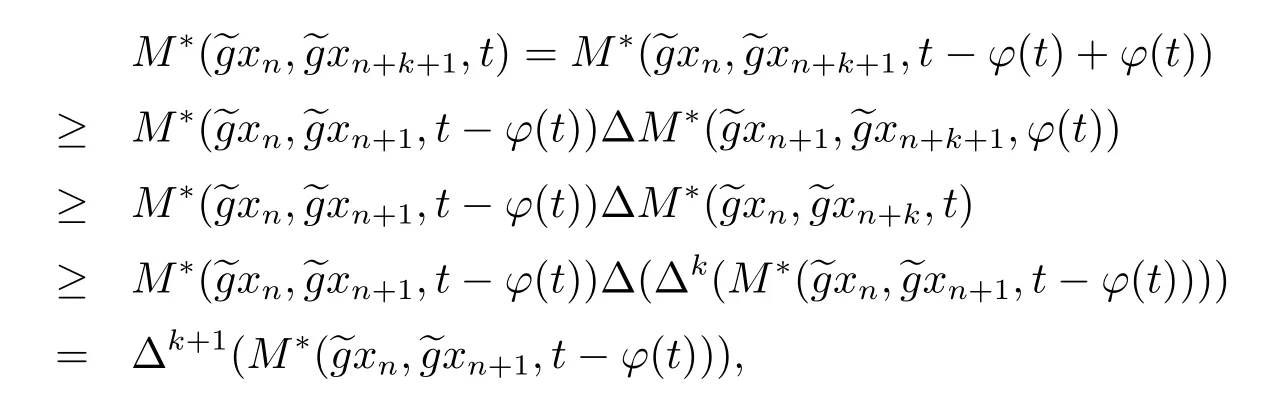
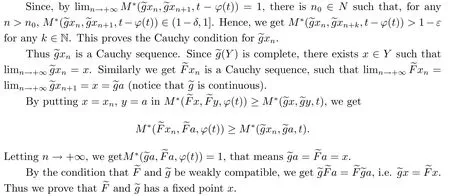
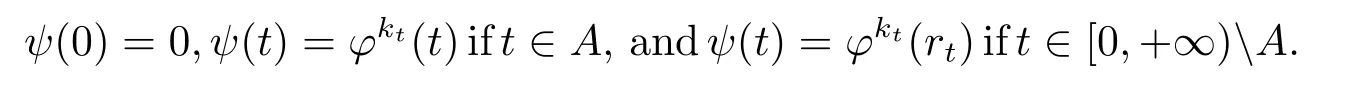
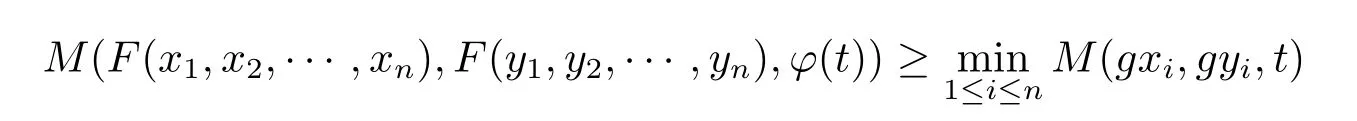

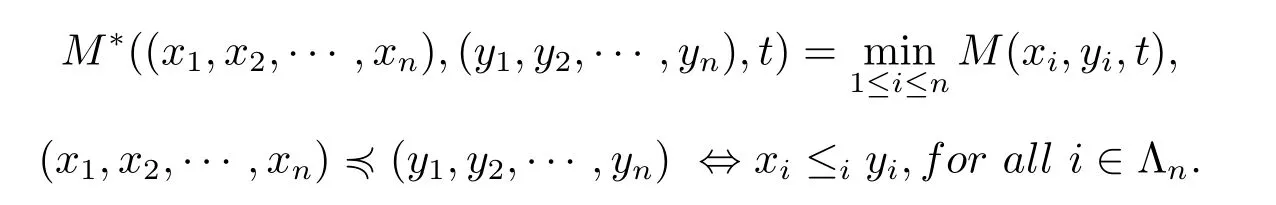


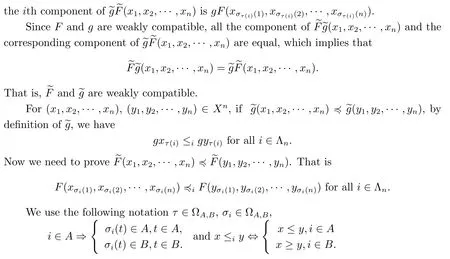

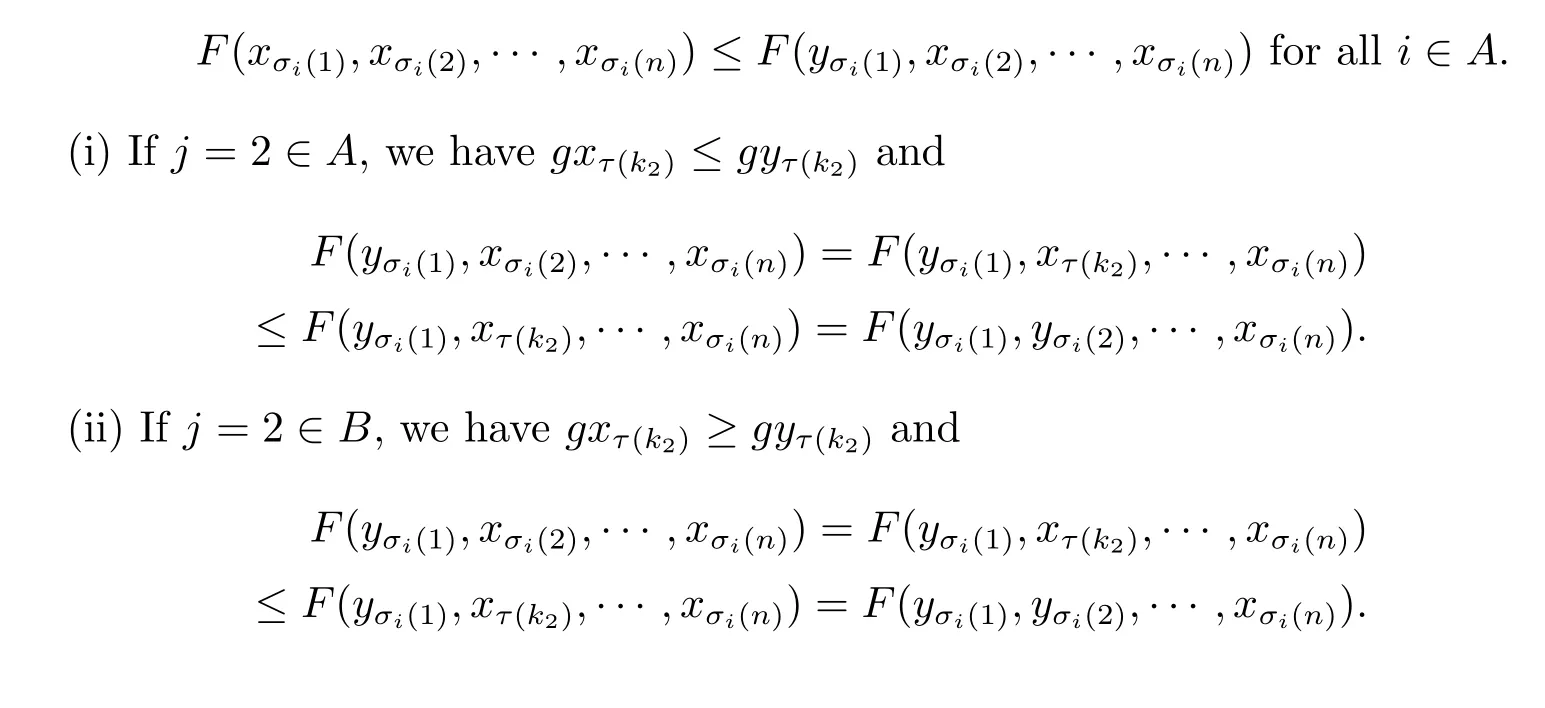
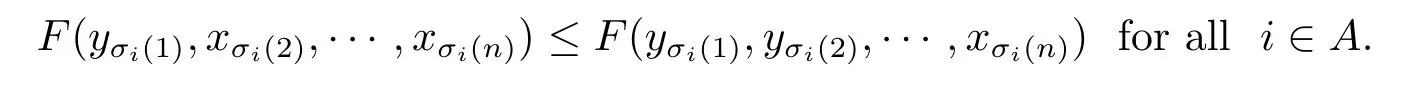
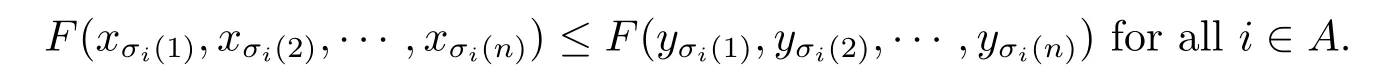

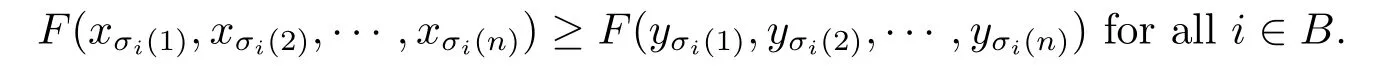

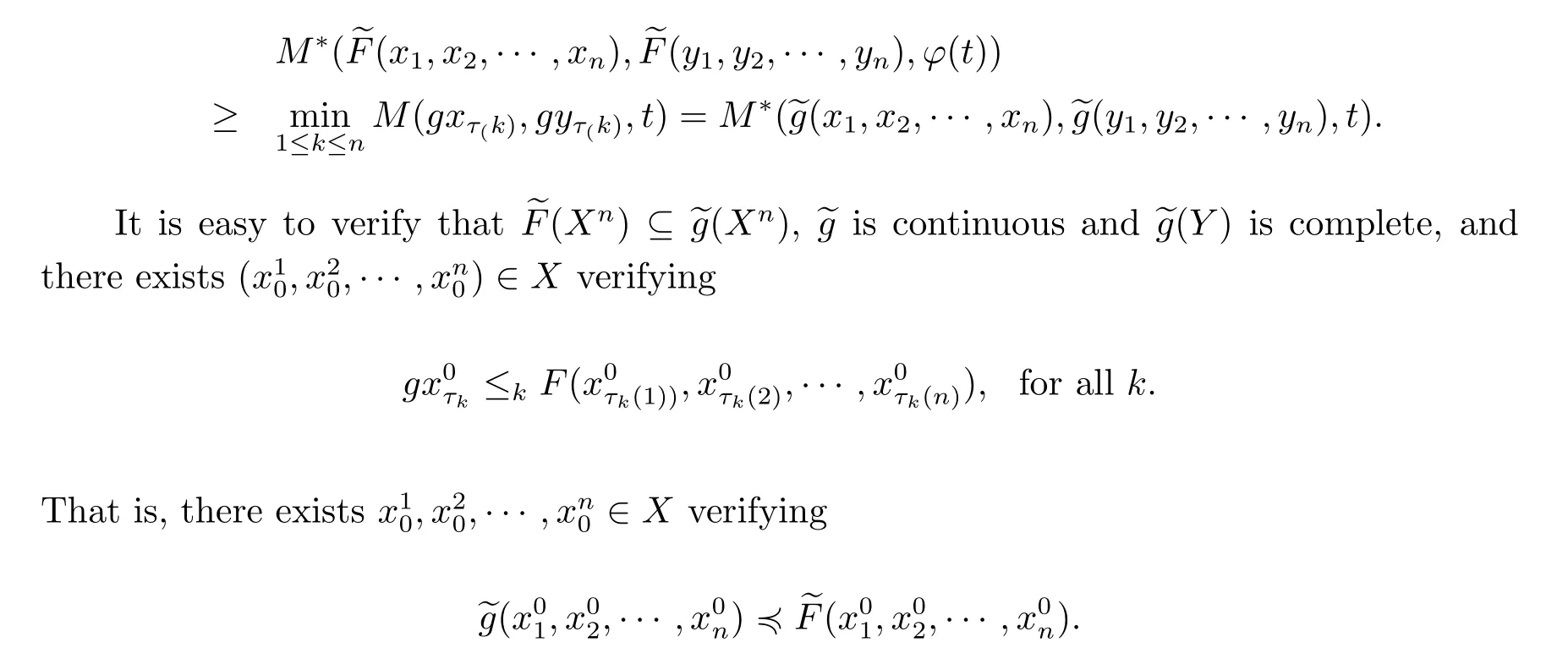
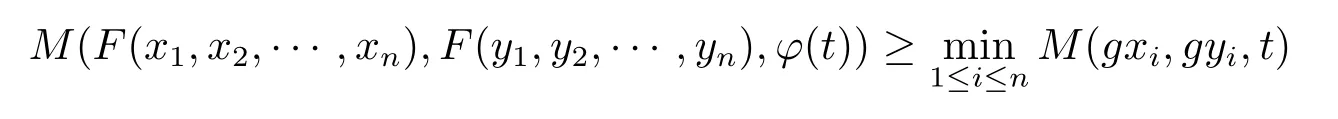
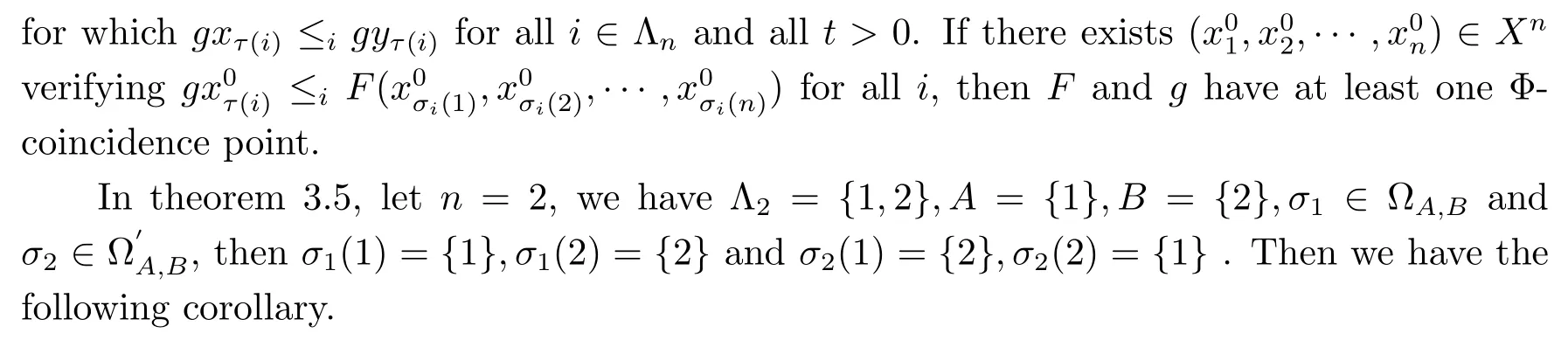
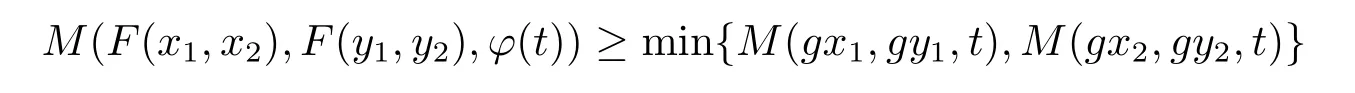
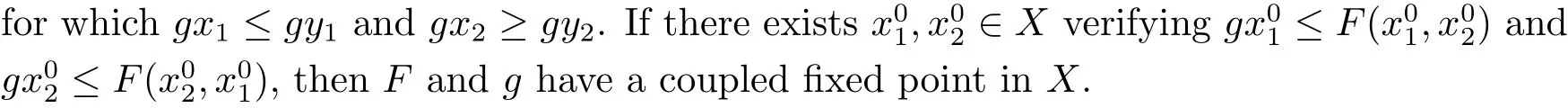


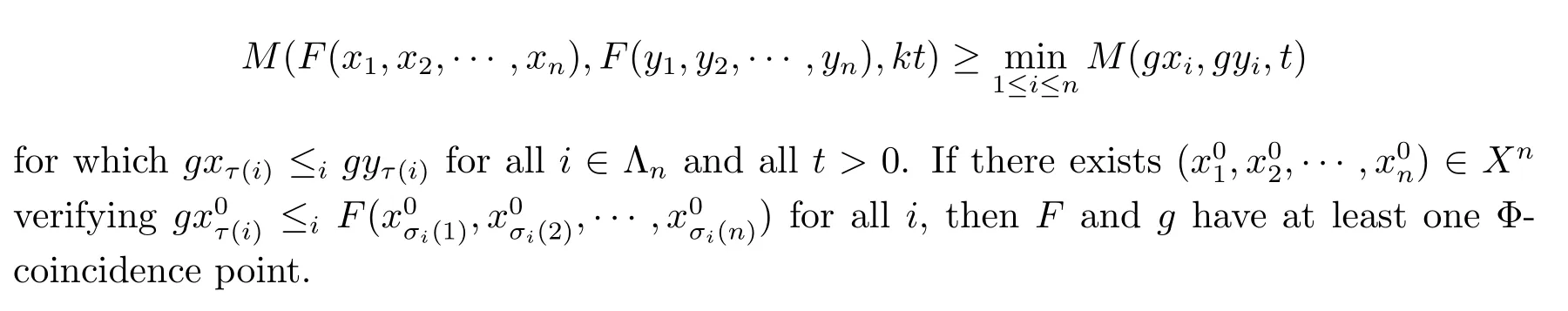

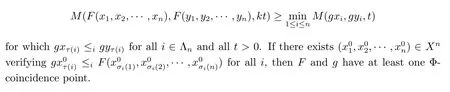
杂志排行
数学杂志的其它文章
- ANNOUNCEMENT ON“MAXIMUM PRINCIPLE FOR NON-UNIFORMLY PARABOLIC EQUATIONS AND APPLICATIONS”
- ANNOUNCEMENT ON“SHARP ERROR ESTIMATE OF BDF2 SCHEME WITH VARIABLE TIME STEPS FOR LINEAR REACTION-DIFFUSION EQUATIONS”
- ON THE CHARACTERIZATION OF COMPACTNESS IN THE SPACE OF HENSTOCK-KURZWEIL INTEGRABLE FUNCTIONS
- K-ORDER GENERALIZED DERIVATIONS OF WEIGHT λ ON δ JORDAN-LIE TRIPLE SYSTEMS
- GRADIENT ESTIMATE FOR POSITIVE SOLUTIONS OF THE PME UNDER GEOMETRIC FLOW
- 一类带记忆项的非经典热方程的爆破问题
