隧道岩体质量智能动态分级KNN方法*
2021-01-15马世伟李守定马立纲李增林张玉锋
马世伟 李守定 李 晓 马立纲 李增林 张玉锋
(①中国科学院地质与地球物理研究所, 中国科学院页岩气与地质工程重点实验室, 北京 100029,中国)(②中国科学院地球科学研究院, 北京 100029,中国)(③中国科学院大学地球与行星科学学院, 北京 100049,中国)(④河北省高速公路延崇筹建处, 张家口 075000,中国)(⑤华北水利水电大学, 郑州 450045,中国)(⑥中铁工程装备集团有限公司, 郑州 450016,中国)
0 引 言
隧道围岩是指隧道周围一定范围内对隧道稳定性产生影响的岩土体,通过现场围岩分级判定既可以对合理选择工程结构参数、工程设计起到指导作用,也是隧道工程投资预算的主要依据(关辉辉等, 2011)。因此一种能够对岩体进行客观评价的围岩分类方法是隧道设计和施工阶段的重要依据。
国际围岩分级方法主要有普氏坚固系数法、岩体质量分级法、RSR 岩石等级结构法、RMR 围岩分级法、Q 值法、日本准围岩抗拉强度分级法、Caotes 岩石分类法、自稳时间 ts法、Terzaghi 荷载分级法等,其中应用范围较为广泛的是Barton的Q值法(Barton et al.,1974; Barton, 2002)和Bieniawski的RMR法(Bieniawski, 1989),国内围岩分级方法主要为国标BQ法,以及基于统计理论、人工智能、类比法思想的分类模型,其中应用范围最为广泛的是《工程岩体分级标准》BQ法(中华人民共和国行业标准编写组, 2014)。Q分类法以岩石质量指标、节理组数、节理粗糙度系数、节理蚀变影响系数、节理水折减系数、应力折减系数6个判定指标为依据。RMR法通过对岩石强度、RQD值、节理间距、节理条件和地下水条件的各项参数进行评分,各得分值相加得到的初值来进行评价。国标BQ法通过岩石单轴抗压强度和完整性程度进行初步评分,通过结构面产状与洞轴走向夹角、地下水系数、地应力系数进行修正。上述几种岩体质量评价方法中,岩石强度是必须获取的参数,岩石强度参数需要进行岩石力学试验确定,存在取样实验时间长,评价不及时等问题,影响隧道施工工艺的制定进而影响施工效率。滞后的围岩评价不仅导致施工效率降低,还存在突发性隧道地质灾害发生的风险。例如延崇高速公路棋盘梁隧道在开挖不到一年时间内发生坍塌5次,云南大风娅口隧道塌方20余次,其中一次严重塌方造成工期延误3个月(吴强, 2009)。因此,防塌、迅速治塌工作已经成为隧道设计和施工人员最为关注的问题之一,而滞后的围岩评价常常降低施工效率,或错过预防突发性施工地质灾害的窗口时间。
岩体工程质量分级通常采用统计方法、回归方法,这些方法需要已知数据分布形式和对变量之间关系的假定,且参数取样时间长,方法多样,评价不及时。在岩石力学与工程系统中,数据分布形式和变量之间的关系是难以准确获知的,传统方法进行岩体分级遇到了困难与挑战(冯夏庭, 1994; 赵洪波等, 2002),快速准确进行隧道工作面岩体质量分级,不仅提高动态施工效率,也降低突发性隧道地质灾害发生的概率。人工智能与岩石力学交叉,提供了一种快速高效的分析方法,不仅克服了传统权系数确定方法的主观性,而且具有快速高效便捷的特点。人工智能与岩石力学交叉在地质工程领域取得了一些成果,如范新宇等(2019)提出了熵权模糊综合评价模型在极软岩隧洞围岩分级中的应用,杨帆等(2019)实现了基于时间序列与人工蜂群支持向量机的滑坡位移预测研究,周翠英等(2019)实现了基于机器学习的地层序列模拟。
目前存在多种人工智能分类方法和算法,分类算法一般分为 Lazy 和 Eager 两种类型。Lazy 学习算法是从局部出发,推迟对训练例子的归纳过程,直到一个新测试例子出现,例如 K 近邻算法、局部加权回归算法等; 而 Eager 学习算法则是从全局出发,在新的测试例子出现之前,由训练例子总结归纳出相似判断目标函数,例如BP神经网络算法、径向基函数、遗传分类方法、粗糙集分类方法等。K 近邻算法(桑应宾, 2009)(KNN)是普遍常用的一种数据挖掘分类算法,该算法具有直观、不需要先验统计知识和无师学习等特点,目前已经成为数据挖掘技术理论和应用研究方法之一(赵睿, 2013)。该方法最早由Cover和Hart在1968年提出(李夕兵等, 2009),在自然科学和社会科学的相关领域得到了广泛应用,包括地质学、经济学、农林学、环境科学等相关学科领域的多个层面。但KNN算法在岩土工程领域的应用很少,对KNN算法进行改进与应用,考虑了实际工程中影响岩体质量的因素(宫凤强等, 2008),试图建立KNN算法模型对岩体质量等级进行预测。KNN 算法的分类原理是通过与分类对象最近的训练样本 k,对于给定测试样本,直接计算该样本和训练集的距离,将距离最近的k个“邻居”点的类别作为参考,作为预测结果返回,样本之间的空间距离一般采用Euclidean 距离计量方式。
该模型应用多项指标作为判别因子,通过改进的KNN算法模型的建立,使用岩体质量判别指标作为KNN算法模型的判别因子,一项指标代表一个维度,围岩级别作为类别标签,通过整理好的训练样本集进行训练,待分类样本集输入KNN算法模型,应用样本判别函数进行类别标签的确定既岩体质量级别的确定,并在延崇高速河北段隧道工程中进行运用。
1 公路隧道岩体质量智能动态分级KNN方法架构
通过深度学习技术提取隧道掌子面照片中岩体质量评价指标相关信息,训练以隧道掌子面照片和特征标签为数据集的卷积神经网络模型,识别掌子面围岩体蚀变程度、结构面风化程度、节理面层间结合情况和地下水状况等分布式特征; 结合岩体裂隙图像智能解译方法统计围岩节理组数和间距来描述隧道掌子面完整程度; 将围岩分级各判别因子通过KNN算法进行分析,获得岩体质量评价结果。
1.1 工作面采用隧道掌子面图片人工智能岩体结构参数辨识方法
工作面采用隧道掌子面图片人工智能岩体结构参数辨识的方法。基于TensorFlow平台应用python语言通过卷积神经网络对图片处理进行结构参数的辨识,具体流程如下:
导入图片数据→预处理→建立模型→训练→可视化→判别指标预测。卷积神经网络模型示意流程图如图1所示:

图1 卷积神经网络模型Fig.1 Convolutional Neural Network Model
柳厚祥等(2018)利用深度学习方法AlexNet模型对隧道掌子面照片进行分析,利用Caffe可视化工具箱提取逐层特征并附加各层的特征直方图,对图片分析提取了掌子面裂隙、涌水、光滑程度等特征,并利用Matlab图像识别技术对岩体节理进一步分析处理得出结构面完整程度代入国标BQ法中进行围岩质量判定,准确率高达87%。因此,通过人工智能深度学习对图片处理并提取围岩判定指标的方法是可行高效的。
论文选用VGG卷积神经网络模型对掌子面所含定性指标如结构面层间结合情况、蚀变程度、风化状态、地下水状况进行判别与提取。VGG模型选用VGG19模型,它含有16个卷积层、3个全链接层、5个池化层,卷积核大小为3×3,学习速率调为0.000,01。
以地下水状况为例进行图片特征识别, 具体过程如图2~图5所示。

图2 潮湿掌子面(图2a); 潮湿掌子面(图2b); 干燥掌子面(图2c); 线状出水(图2d)Fig.2 a.Wet palm surface; b.wet palm surface; c.dry palm surface; d.linear effluent

图3 训练集与迭代次数关系Fig.3 Relationship between training set and number of iterations

图4 测试集与迭代次数关系Fig.4 Test set versus number of iterations

图5 部分图片特征识别输出结果Fig.5 Output Results of Partial Image Feature Recognition
1.2 采用人工智能方法进行评价
通过人工智能深度学习方法对掌子面图片所含相关判定指标进行提取,将这些判定指标导入KNN算法模型进行处理,得到岩体质量评价结果。通过Anaconda Navigator软件中的Spyder应用python语言编写改进的KNN分类算法,将KNN算法分类模型的判别因子即模型中的每一个维度的权重值导入算法模型中并对其判别结果进行输出。
2 延崇高速公路隧道地质条件及围岩质量特征
2.1 工程地质条件
延崇高速河北段隧道区域位于张家口市东部怀来、赤城、崇礼三县,地处冀西北山地阴山—燕山构造带(图6)。
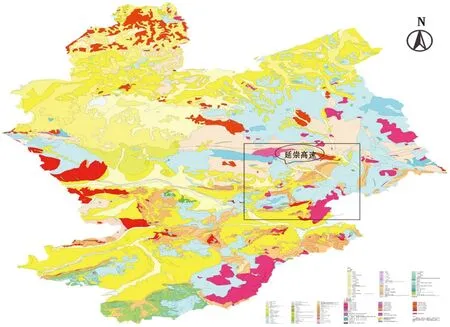
图6 张家口市1︰5万地质图Fig.6 ,1︰50,000 geological map of Zhangjiakou City

2.2 水文地质条件
该区地下水主要为基岩裂隙水,局部以孔隙水为主。地下水来源主要为大气降雨,排泄方式以地下水径流、河水排泄及人工开采为主。河流径流量多集中于7~9月份,具有水流急、陡长陡落、洪水季节携带泥沙等特点。地下水径流受地形影响较大,多属紊流运动,一般沟谷内富水程度中等-强,山脊及山坡处富水程度弱,局部沟谷内可见泉水及地表径流。
2.3 区域内不良地质条件
路线穿越区地质灾害和不良地质作用主要为潜在不稳定边坡、断层、风吹雪、高地应力等。
2.3.1 不稳定边坡
赤城南互通段路线穿越洪积扇前缘,该段地表出露以洪积碎石层为主,边坡自然稳定。线路施工开挖导致左侧坡面存在临空面,碎石滚落现象时有发生,为潜在不稳定边坡,需要进行边坡支护处理。
2.3.2 断层
杏林堡隧道K28+880处,掌子面岩性发生变化,掌子面右侧围岩为中上元古界长城系高于庄组石英砂岩、砂质白云岩、角砾状白云岩和黑色页岩,强风化,层间结合一般。掌子面左侧为侏罗系中统髫髻组中性火山岩夹凝灰质砂岩,断层产状为267°∠45°。
2.3.3 风吹雪
K95+000至终点段常年西北风且风力较大,冬季降雪后,容易在山区沟谷东南坡形成积雪。
2.3.4 高地应力
路线穿越区域的松山特长隧道、杏林堡特长隧道,最大埋深400~800,m,岩性为花岗岩、安山岩、页岩、片麻岩。受高地应力影响,隧道开挖过程中松山隧道坚硬花岗岩由于弹性势能的突然释放易形成岩爆灾害,杏林堡特长隧道页岩、全风化片麻岩等软岩区域易引发挤压大变形灾害。实际施工过程中高地应力特征表现并不明显。
2.4围岩质量特征
对延崇高速河北段隧道8个标段1300份围岩分级报告进行统计,结果如图7所示。现场以Ⅳ级围岩为主约占总里程53%, Ⅴ级围岩最少约占总里程10%。以国标BQ法为基础围岩分为Ⅲ、Ⅳ、Ⅴ级3类,将评价指标输入KNN算法模型,经训练样本训练,输入测试数据,通过KNN算法模型计算输出Ⅲ、Ⅳ、Ⅴ级3类围岩级别。
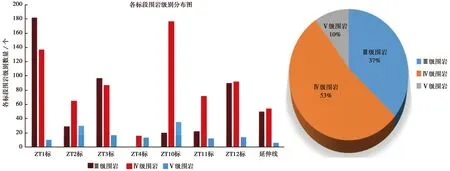
图7 围岩质量特征统计分布图Fig.7 Statistical distribution of mass characteristics of surrounding rock
3 KNN算法分类模型
KNN算法是在已知训练集数据和标签时输入测试数据,将测试数据的特性与训练集的相应特性进行比对,找到与训练集相似的前K个数据,则测试数据对应的类别是K个数据最频繁出现的类别(王慧, 2017)。
3.1 距离度量
KNN算法的核心是计算待分类样本与训练样本之间的距离,论文采用欧氏距离法来确定样本的相似性(陈磊磊, 2015)。欧氏距离公式为:
(1)
式中:X=(x1,x2,x3…,xn)和Y=(y1,y2,y3…,yn)分别代表两个样本数据,n为样本特征属性的个数。
3.2 改进的KNN算法
传统的KNN算法未考虑每个特征指标对分类结果信息的贡献程度不同,在传统的KNN算法步骤中使用熵值法对特征指标赋予权重(张慧等, 2018),得到的分类结果更为精确。
设有m个数据样本,n个样本特征指标,存在数据矩阵M=(∂ij)m×n。
(1)第j项指标中的第i个样本数据占j指标下总体样本的比重qij
(2)
(2)计算第j项指标的信息熵hj
(3)
(3)计算第j项指标的熵值ej
ej=khj
(4)
其中:k=1/1,nm
(4)计算差异性系数gj:gj=1-ej
(5)定义特征指标的权数:
(5)
熵值法赋予权重是一种客观赋权方法,有效避免了人为主观性对指标重要性的影响,有科学的理论依据。
3.3 KNN算法的模型建立
将一个分类算法抽象为系统参数(k,w,h)、类别标签Y、距离函数d、样本分类函数Y(Xi)、样本判别函数e、训练样本集XW、待分类样本集XD。其定义如下(李昂, 2018):
(1)系统参数中(k,w,h),k表示某一个样本点X的最近邻个数; 分量权重向量W=(w1,w2,w3…,wn)分別表示在计算距离时,样本点向量X每一个维度的权重值,赋权过程按照式(2)~(5)进行; 距离权重向量h=(h1,h2,h3…,hn)表示某一样本点X的最近邻集合中每个样本点的权重,论文每个样本点的权重相同。
(2)用一个n维向量X=(X1,X2,…,Xn)表示一个样本点。对于某一个样本点X来说,KNNXi={X1,X2,…,XK}, 表示的是与Xi最近的k个邻居样本点的集合。
(3)类别标签集Y={Y1,Y2,…Ym}是系统中所有类别标签。对于一个待分类的样本点Xi.,其分类结果可以表示为:
Y(Xi)=argmax∑yi∈Y∑X∈KNNXic(X,yi)
(6)
若Y(X)=yi表示样本点X对应的类别标签为yi; 别特地,若某些样本X的类别标签未被确定,则Y(X)=⊥。
(4)距离函数d:采用欧氏距离进行距离测量:
(7)
(5)样本判别函数c:Rn×N→{0, 1}用于判断样本点是否属于某一类别,若c(X,yi)=1表示样本点X属于类别yi,若c(X,yi)=0则表示样本点X不属于类别yi。
(6)训练样本集XW={XIY(X)≠⊥}是一个类别签已知的样本点集合。
(7)待测样本XD={XIY(X)=⊥}是一个类别标签未知的样本点集合。
4 公路隧道岩体质量智能动态分级KNN方法
4.1 判别指标的确定及量化
岩体是具有一定构造的地质体。影响岩体质量等级的因素主要有3个:岩体性质、岩体结构和赋存环境。统计表明国内外围岩分级方法(表1)应用最为广泛的分级指标为岩石强度、岩石完整程度、地下水状况、结构面状态、初始应力状态。延崇高速河北段隧道区域高地应力影响甚微暂不考虑; 考虑到岩石强度的确定需要进行现场和室内试验及分析,岩体质量评价时间滞后,常常降低施工效率,论文采用岩体蚀变程度、风化状态进行表示; 岩石完整程度通过节理条数、岩体体积节理数Jv进行表示; 结构面状态通过结构面走向与洞轴夹角、层间结合情况来表示。最后确定以体积节理数Jv、节理条数、岩体风化程度、岩体蚀变程度、结构面走向与洞轴夹角、结构面层间结合情况和地下水状况7项指标作为KNN算法模型的判别因子。

表1 岩体质量分级指标Table1 Classification index of rock mass quality
根据RMR岩体质量评价方法将风化程度、岩体蚀变程度、结构面层间结合情况和地下水状况等定性描述进行量化,如表2所示。

表2 定性描述量化表Table2 Qualitative description quantitative table
基于python实现各指标与围岩级别相关性分析(图8),由图可知7个判定指标与围岩级别都具有较好的相关性。

图8 相关性分析Fig.8 Correlation analysis
4.2 改进KNN算法分类模型的建立
根据延崇高速河北段围岩分级单位提供的8个隧道, 40个掌子面实测资料为例,选取150个样本数据进行学习,再选取50个样本数据作为待判定样本进行检验,并以体积节理数、节理组数、风化程度、岩体蚀变程度、结构面走向与洞轴夹角、结构面层间结合情况和地下水状况作为KNN算法分类模型的判别因子即模型中的每一个维度,将围岩级别输出为Ⅲ、Ⅳ和Ⅴ级3个类别。
通过Anaconda Navigator软件中的Spyder应用python语言编写改进的KNN分类算法,将KNN算法分类模型的判别因子即模型中的每一个维度值导入算法模型中并对其判别结果进行输出,具体流程如图9所示。

图9 KNN算法围岩分级流程图Fig.9 KNN Flow chart of surrounding rock classification of algorithm
4.3 判别模型的检验
以延崇高速公路河北段隧道岩体质量评价方法(国标BQ法)计算得出的隧道围岩级别作为实测值进行模型输出结果的校验,具体计算方法如下(中华人民共和国行业标准编写组, 2014):
岩体基本质量指标BQ,应根据分级因素的定量指标Rc与Kv,按下式进行计算。
BQ=100+3Rc+250Kv
(8)
式中:BQ为岩质围岩基本质量指标;Rc为岩石单轴饱和抗压强度;Kv为岩体完整系数。
地下工程岩体质量指标[BQ],按下式计算:
[BQ]=BQ-100(K1+K2+K3)
(9)
式中:[BQ]为岩质围岩基本质量指标修正值;K1为地下水状态影响修正系数;K2为主要软弱结构面产装影响修正系数;K3为初始地应力状态影响修正系数。
使用训练完成的KNN算法分类模型对50个待判别样本进行判别,其中误判5个样本,其余45个样本判别结果与国标BQ法判别结果完全相符(表3)。发生误判的原因可能是:训练样本数据量不足、训练样本的代表性以及容量的范围需要进一步优化和改善。
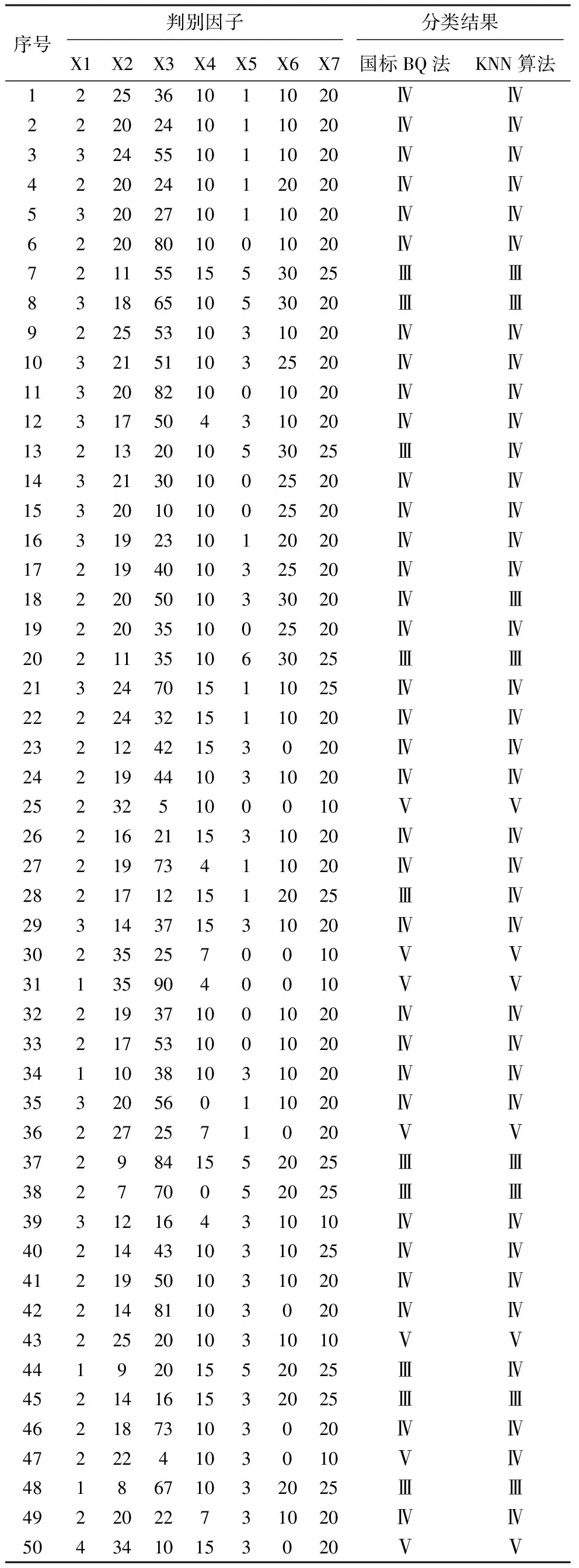
表3 改进的KNN算法模型分类结果Table3 Classification results of improved KNN model
改进的KNN算法分类模型误判率为:
η=5/50=0.10
由此可见,改进的KNN算法分类模型在隧道岩体工程质量等级判别和分类中的应用,是完全可行且高效的。
5 结 论
(1)公路隧道岩体质量智能动态分级KNN方法一种利用人工智能技术快速高效进行岩体质量动态分级的方法,能够在现场实时获得岩体质量评价结果。
(2)KNN分级方法中选用了7个判别指标,综合考虑了隧道围岩体的结构、赋存环境、地质构造等特性,并体现了这些指标在实际工程评判中的可操作性和适用性。
(3)KNN分级方法误判率低,在判别分类中排除了评分过程中人为因素的影响,具有较强的判别能力,为TBM围岩实时分级做方法储备。
