FRP筋-ECC梁受弯性能

2021-01-15周甲佳姚少科张丽娟

建筑科学与工程学报 2020年6期

周甲佳，姚少科，景川，赵军，张丽娟

(1. 郑州大学力学与安全工程学院，河南郑州 450001； 2. 中国科学院大学工程科学学院，北京 100049； 3. 国网河南省电力公司经济技术研究院，河南郑州 450052)

0 引言

钢筋混凝土结构构件在土木工程领域有着广泛的应用，然而，由于混凝土抗拉性能差、易开裂和钢筋耐腐蚀性差的缺点，导致钢筋混凝土结构耐久性差，严重影响钢筋混凝土结构构件的服役寿命。

为了解决钢筋混凝土结构的耐久性问题，学者们研发出了耐腐蚀性强的纤维增强复合材料筋(FRP筋)代替混凝土结构中的钢筋，这是解决混凝土结构耐久性问题的有效方法。与钢筋相比，FRP筋具有轻质、高强、耐疲劳、耐腐蚀性强、防磁性能好、轴向热膨胀系数低等优点[1]，更适用于恶劣的环境中。然而FRP筋单轴拉伸力学性能表现为线弹性，当其与脆性的混凝土结合使用时，相较于钢筋混凝土结构，其延性较低，同时有发生脆性破坏的风险。此外，FRP的弹性模量低，将使FRP混凝土结构构件变形增大，具有较大的裂缝宽度和挠度，影响其正常使用[2-5]。这些缺点使得FRP筋在混凝土结构中的应用受到限制。

高延性纤维增强水泥基复合材料(ECC)的出现为上述问题的解决提供了可能。ECC是Li[6]基于微观力学性能对材料进行优化设计得到的。研究表明，当纤维含量(体积分数)在2%时，ECC在拉伸作用下表现出多缝开裂和应变硬化的特性，并具有良好的控制裂缝宽度的能力[7]。与普通混凝土相比，ECC具有韧性好、耐久性能好、耗能能力高、抗剪能力强等优点，可用于桥梁工程、抗震工程中。因此，其问世以来，便受到学者的广泛关注[8-12]。

已有研究表明：ECC与FRP筋配合使用可以增大结构的延性，减小结构的裂缝宽度，从而弥补FRP筋混凝土结构构件延性低的缺点。如Li等[13]最早对GFRP-ECC梁进行了静力弯曲试验，结果表明：相同配筋率的ECC梁在延性、承载能力、抗剪能力等方面均优于高强混凝土梁；使用ECC替代高强混凝土，可以减少甚至完全不使用抗剪钢筋。Yuan等[14]对BFRP筋-ECC梁及BFRP筋-ECC/混凝土复合梁进行了静力弯曲试验，发现配筋率相同时，ECC梁的极限承载力和变形力分别为BFRP筋混凝土梁的1.2倍和1.5倍；无腹筋ECC梁的极限承载能力及变形能力与配置箍筋的BFRP混凝土梁基本相同，而且破坏过程呈现出延性的特征；当ECC配置于BFRP筋增强混凝土梁的受拉区时可有效控制裂纹宽度。何佶轩[15]对FRP筋-ECC梁和混凝土/ECC复合梁进行了抗剪试验，发现FRP筋-ECC梁的抗剪承载力为相同配筋率混凝土梁的1.9倍；受拉区采用ECC取代混凝土时，若ECC的厚度为30%梁高，组合构件的受剪承载力可达到全ECC梁的95%。王必元[16]对FRP筋-ECC/混凝土复合梁受弯性能进行了试验研究，结果表明：随着ECC对混凝土替换率的增加，裂缝宽度明显减小，延性增大。Cai等[17]用有限元方法对FRP-ECC梁和FRP-混凝土梁进行了模拟，结果表明：FRP-ECC梁比FRP-混凝土梁具有更好的延性、裂缝控制能力。

然而，这些研究仅限于试验研究和数值模拟方面，对于FRP筋-ECC结构构件的相关计算理论方面的研究仍有待加强。为此，本文对FRP筋-ECC梁进行了正截面受力分析，推导了其极限抗弯承载力计算公式，并将计算结果与已有试验结果进行对比。基于本文的理论计算方法，对不同ECC抗压强度和不同配筋率的FRP筋-ECC梁进行了参数分析，可供实际工程应用参考。

1 基本假定

为简化计算，借鉴钢筋混凝土结构设计基本理论[13]，本文对FRP筋增强ECC梁受弯全过程分析时采用如下基本假定：

(1)平截面假定，即荷载作用下ECC梁的截面始终保持平面，ECC的应变沿截面高度呈线性变化。

(2)不考虑ECC与FRP筋之间的相对滑移，相同位置的ECC和FRP筋变形协调。

(3)在梁的整个受弯过程中，跨中的曲率φ和挠度f始终呈正比例关系。

(4)ECC单轴拉伸状态下应力-应变(σ-ε)关系如图1所示，其中，σtc和εtc分别为ECC的初裂应力和初裂应变，σtu和εtu分别为ECC的极限抗拉强度和极限拉应变。

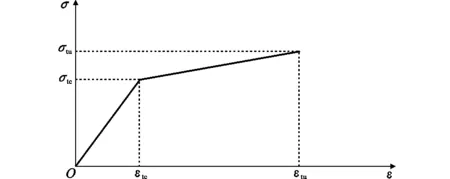
图1ECC单轴拉伸应力-应变曲线Fig.1Uniaxial Tensile Stress-strain Curve of ECC

ECC单轴拉伸本构关系的数学表达式为

(1)

式中：εt为ECC的拉应变；σt为ECC的拉应力。

(5)ECC单轴压缩状态下应力-应变关系如图2所示，其中，σc0和εc0分别为ECC的峰值压应力和峰值压应变，ε0.4为ECC压应力σc=0.4σc0时对应的压应变，εcu为极限压应变。

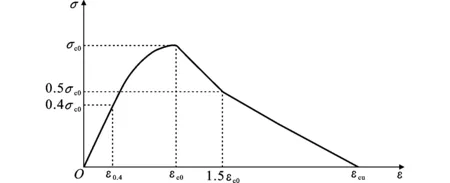
图2ECC单轴压缩应力-应变曲线Fig.2Uniaxial Compressive Stress-strain Curve of ECC

ECC单轴压缩本构关系的数学表达式为[18]

(2)

式中：εc为ECC的压应变；E0为ECC的弹性模量；a0，b0为拟合参数，a0=0.308，b0=0.124。

(6)不考虑不同抗压强度ECC的极限压应变的变化。

(7)FRP单轴拉伸应力-应变曲线见图3，其中，fy，εy分别为FRP的极限拉应力和极限拉应变。

图3FRP筋单轴拉伸应力-应变曲线Fig.3Uniaxial Tensile Stress-strain Curve of FRP Bar

FRP单轴拉伸本构关系的数学表达式为

σf=Efεf0≤εf≤εy

(3)

式中：σf为FRP的拉应力；εf为FRP的拉应变；Ef为FRP的弹性模量。

2 FRP筋增强ECC梁受弯全过程理论分析

基于已有试验研究结果[8]可知，FRP筋增强ECC梁的受弯过程可分为3个阶段：弹性阶段、带裂缝工作阶段和破坏阶段。

2.1 弹性阶段

外荷载很小时，受拉区边缘ECC未达到初裂应变，所有的材料都处于线弹性阶段。此时，截面上的应变和应力均呈线性分布，梁处于弹性阶段，其弯矩-曲率关系是线性的。在此阶段，梁横截面上的应变和应力分布如图4所示，其中h为截面高度，b为截面宽度，c为受压区高度，s为FRP筋到受拉区边缘的距离，Af为FRP筋面积。

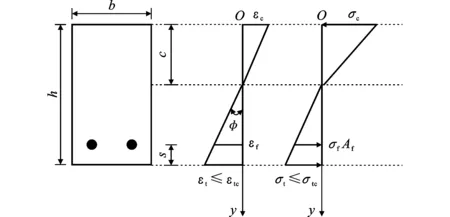
图4弹性阶段应变和应力分布Fig.4Strain and Stress Distributions at Elastic Stage

此时截面上任意一点ECC的应力表达式为

(4)

式中：y为截面上的点到上边缘的距离。

2.2 带裂缝工作阶段

随着外荷载的增加，受拉区边缘的ECC会达到初裂应变而开裂，随后，裂缝逐渐向上扩展，受拉区ECC的应力开始出现非线性分布，梁进入带裂缝工作阶段。

(1)带裂缝工作阶段前期，受压区边缘ECC应变未超过ε0.4，受压区ECC的应力仍然处于线弹性阶段，截面上应变和应力分布如图5所示。

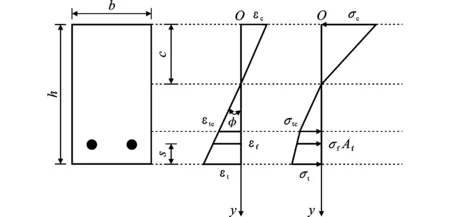
图5受压区应力线性分布时应变和应力分布Fig.5Strain and Stress Distributions with Linear Stress Distribution in Compression Zone

此时截面上任意一点ECC的应力表达式为

(5)

式中：a为截面上应变εtc处所对应的截面高度。

(2)外荷载增大到一定程度时，受压区边缘ECC会进入本构关系的第二阶段，受压区ECC应力开始出现非线性分布，截面上应变和应力分布如图6所示。

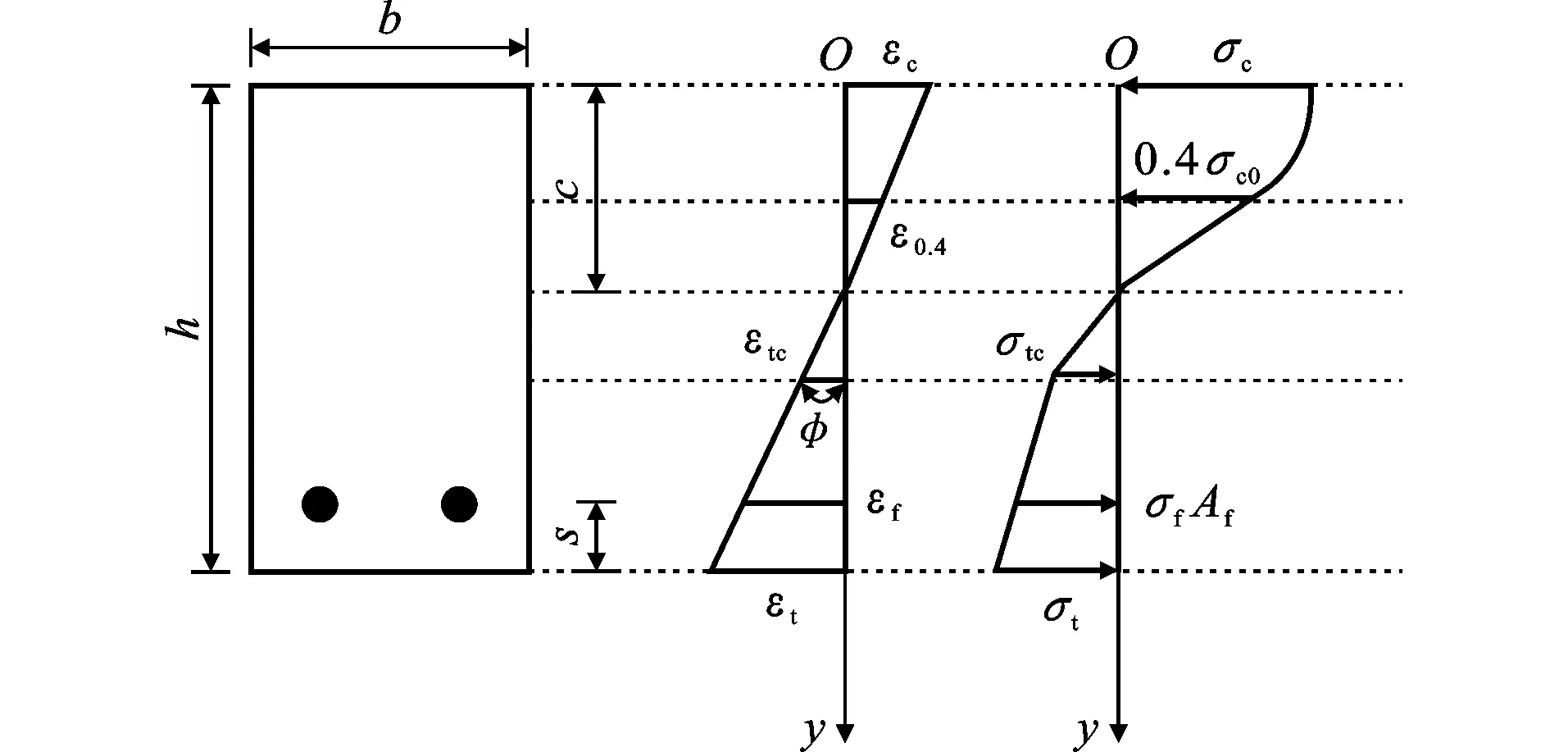
图6受压区应力开始非线性分布时应变和应力分布Fig.6Strain and Stress Distributions when Stress of Compression Zone Started to Enter Nonlinear Stage

此时截面上任意一点ECC的应力表达式为

(6)

式中：c1为截面上应变ε0.4处所对应的截面高度。

(3)外荷载继续增大，受压区边缘ECC进入应力-应变关系的第三阶段，其应力开始随着应变的增大而减小。截面上应变和应力分布如图7所示。

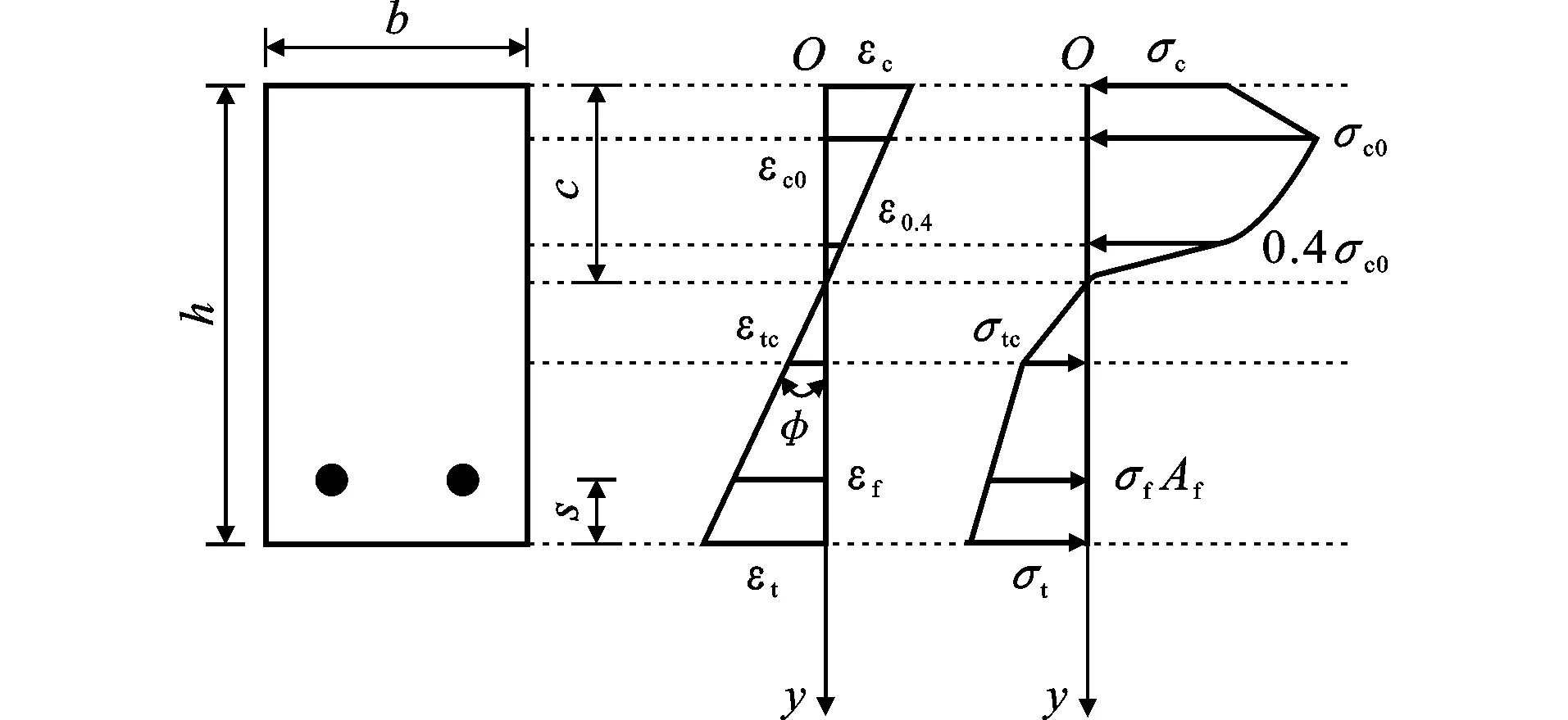
图7受压区应力包括三部分时应变和应力分布Fig.7Strain and Stress Distributions when Stress of Compression Zone Contains Three Parts

此时截面上任意一点ECC的应力表达式为

(7)

式中：c2为截面上应变εc0处所对应的截面高度。

(4)外荷载继续增大，受压区边缘的ECC进入本构关系第四阶段。截面上应变和应力分布见图8。

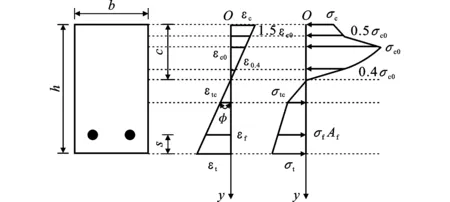
图8受压区应力包括四部分时应变和应力分布Fig.8Strain and Stress Distributions when Stress of Compression Zone Contains Four Parts

此时截面上任意一点ECC的应力表达式为

(8)

式中：c3为截面上应变1.5εc0处所对应的截面高度。

2.3 破坏阶段

外荷载继续增加，FRP筋达到极限拉应变或受压区边缘ECC达到极限压应变时，梁将达到极限破坏状态，发生破坏。

极限破坏状态下，受压区高度c的计算公式为

(9)

将截面破坏类型分为以下3类：

(1)FRP筋达到极限拉应变，同时受压区边缘ECC达到极限压应变，称为界限破坏。

界限破坏的受压区高度ca为

(10)

(2)FRP筋达到极限拉应变，受压区边缘ECC没有达到极限压应变，称为受拉破坏。该破坏类型的表现为FRP筋被拉断。此时，极限弯矩Mu为

(11)

(3)FRP筋没有达到极限拉应变，受压区边缘ECC达到极限压应变，称为受压破坏。该破坏类型的表现为受压区边缘ECC被压碎。此时，极限弯矩为

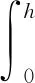
(12)

为简化极限弯矩的计算，将受压区ECC的应力图形和受拉区ECC的应力分别用2个等效的矩形应力图形来代替，如图9所示，其中x为有效受压区高度，xt为有效受拉区高度，α1，α2为相关参数。

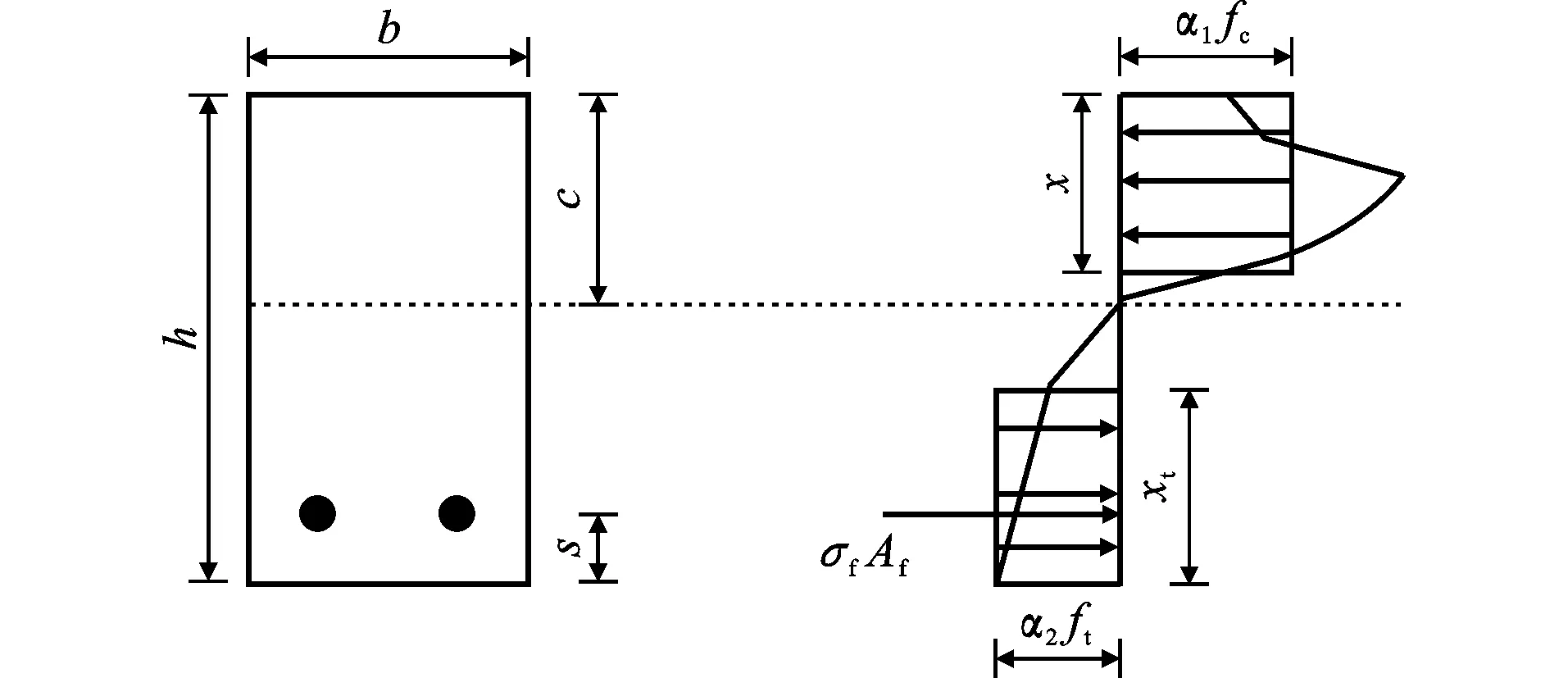
图9等效矩形应力图Fig.9Equivalent Rectangular Stress Diagram

等效矩形应力图计算公式为

(13)

式中：β1，β2为相关参数。

计算公式中的系数可以按下列原则确定：受压区ECC压应力合力的大小和作用点位置不变，受拉区ECC拉应力合力的大小和作用点位置不变。

按照上面的原则进行数值计算，公式如下

(14)

(15)

由式(14)可推导出参数β1，α1的计算公式如下

(16)

由式(15)可推导出参数β2，α2的计算公式如下

(17)

不同抗压强度和配筋率取值下的各参数计算结果如表1所示。

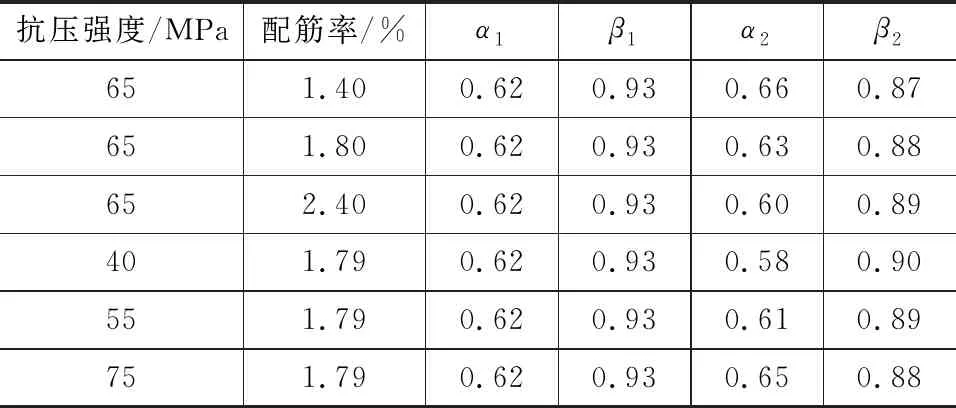
表1参数计算结果Tab.1Calculation Results of Parameters

通过对表1的数据进行分析，极限状态下对参数取值的建议为：α1，α2，β1，β2分别取0.62，0.63，0.93，0.88。

3 模型验证

为验证本文提出的FRP筋增强ECC梁受力全过程计算模型的正确性，采用MATLAB对编号为GRE16的GFRP-ECC试件[8]进行了数值计算。

3.1 试验简介

承受对称集中荷载P作用的FRP筋-ECC梁如图10所示。采用的FRP筋抗拉强度为740 MPa，弹性模量为40 GPa，筋材直径为12.9 mm。采用的ECC抗压强度为75 MPa，试件的截面尺寸如图11所示，其中加载点到支座间的距离为629 mm。

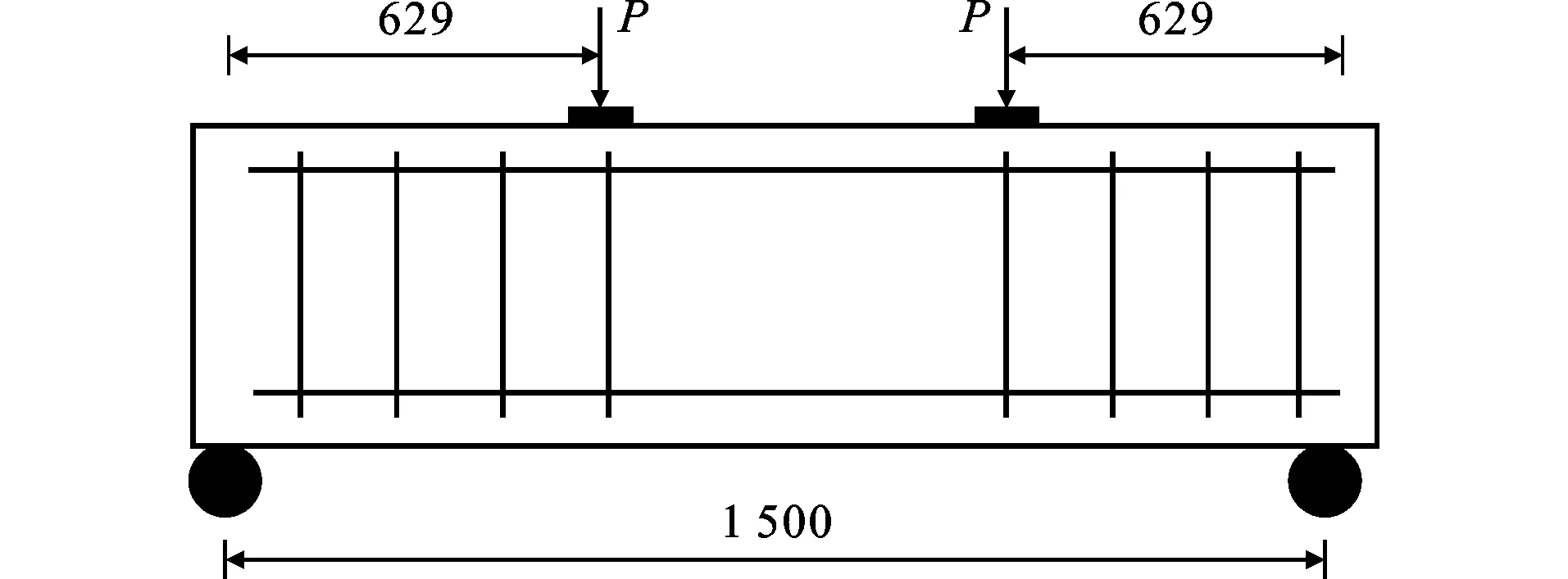
图10试验示意图(单位:mm)Fig.10Schematic Diagram of Experiment (Unit:mm)

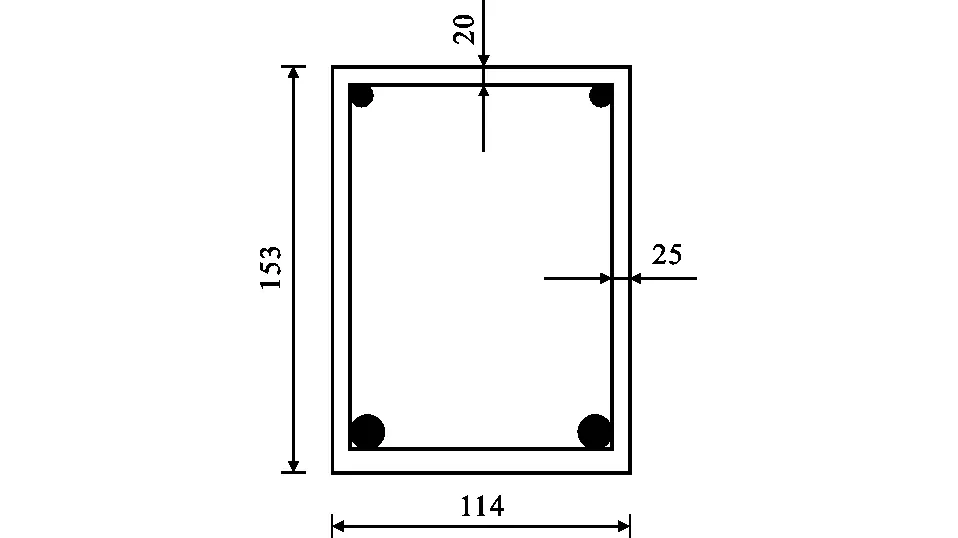
图11试件截面(单位:mm)Fig.11Cross Section of Specimen (Unit:mm)

3.2 试验值与计算值对比

获得的弯矩-挠度计算值与试验值的对比如图12所示。由图12可以看出，试验值和计算值十分接近，证明了本文提出的理论和计算方法的正确性。

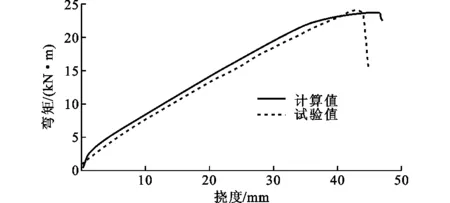
图12试件GRE16的弯矩-挠度曲线Fig.12Moment-deflection Curve for Specimen GRE16

4 ECC抗压强度和FRP筋配筋率对梁受弯性能影响分析

基于本文提出的模型，采用MATLAB对FRP筋-ECC梁进行了参数分析，分析了ECC抗压强度和配筋率对梁受弯性能的影响。

4.1 ECC抗压强度对梁受弯性能影响

本文对配筋率为0.89%，ECC抗压强度分别为40，55，65 MPa的FRP筋-ECC梁进行了计算分析。基于MATLAB分析可知：当ECC的抗压强度为40 MPa时，梁破坏类型为受压破坏；随着抗压强度的增加，当ECC的抗压强度为55 MPa和65 MPa时，梁的破坏类型变为受拉破坏。这说明配筋率为0.89%时，随着ECC抗压强度的增加，FRP筋-ECC梁的破坏模式由ECC的受压破坏转变为FRP筋的受拉破坏，其弯矩-曲率(M-φ)关系曲线如图13所示。

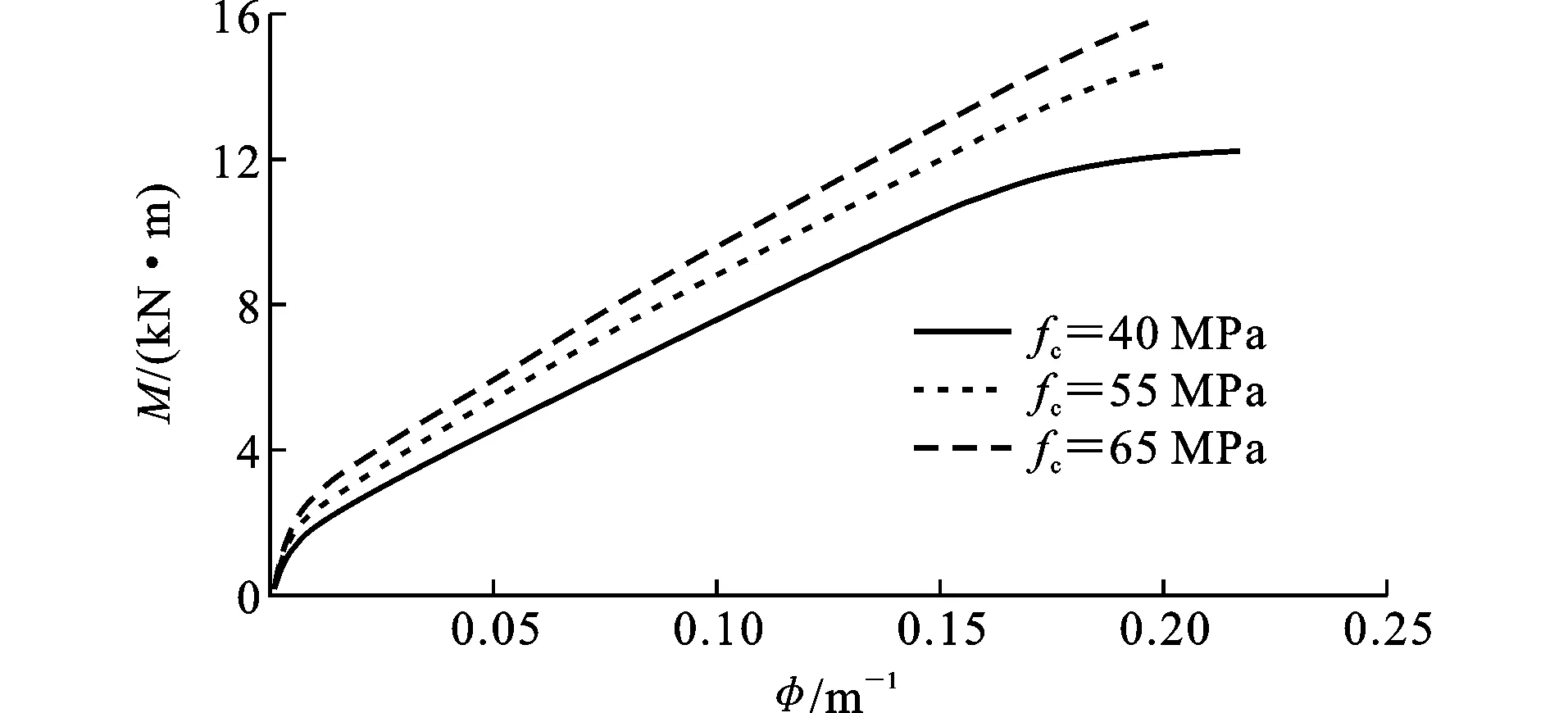
图13不同ECC抗压强度的梁弯矩-曲率关系Fig.13Moment-curvature Relationship for Beams with Different Compressive Strengths of ECC

由图13可知，在弹性阶段，ECC抗压强度对FRP筋-ECC梁弯矩-曲率曲线的斜率有一定影响，ECC抗压强度越大，斜率越大。这说明当FRP筋配筋率相同时，ECC的弹性模量对FRP筋-ECC梁的初始刚度有较为明显的影响。随着ECC单轴抗压强度的增加，FRP筋-ECC梁的初始刚度逐渐增大。

不同强度ECC梁的开裂荷载不同，随着ECC抗压强度的增加，开裂荷载逐渐增大。ECC开裂后，弯矩随着曲率的增大继续增加，但ECC抗压强度对梁弯矩-曲率曲线的斜率影响变小。这是由于ECC开裂后，梁的刚度由ECC抗压强度和FRP筋配筋率共同决定，而各试件的FRP筋配筋率没有差别。当梁破坏时，FRP筋-ECC梁的极限承载力随着ECC抗压强度的增加而逐渐增大。

4.2 配筋率对梁受弯性能的影响

为分析配筋率对FRP筋-ECC梁受弯性能的影响，本文对抗压强度为65 MPa，不同配筋率的FRP-ECC梁进行计算分析。基于MATLAB分析可知：当配筋率ρf为0.36%～0.97%时，梁破坏类型为受拉区FRP筋的拉断破坏；随着配筋率的增加，当配筋率为1.4%～2.4%时，梁的破坏类型变为受压区ECC的受压破坏。这说明当ECC抗压强度一定时，随着FRP筋配筋率的增加，FRP筋-ECC梁的破坏模式由FRP筋的受拉破坏转变为ECC的受压破坏，其弯矩-曲率关系曲线如图14所示。

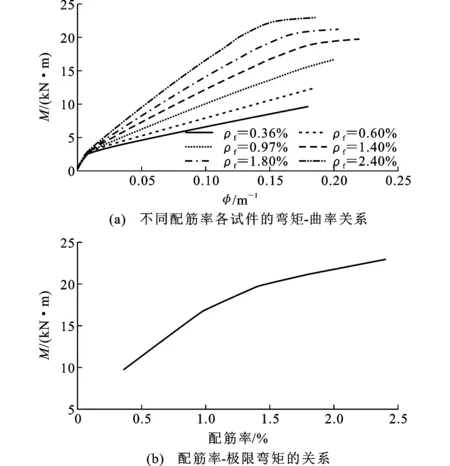
图14配筋率对试件弯矩-曲率关系的影响Fig.14Effects of Reinforcement Ratio on Moment-curvature Relationship for Specimens

由图14(a)可知，当FRP筋-ECC梁处于弹性阶段时，各梁构件的弯矩-曲率关系曲线呈线性变化，而且配筋率对FRP筋-ECC梁初始刚度及开裂弯矩的影响很小，几乎可以忽略不计。这是由于弹性阶段，FRP筋和ECC的应变均较小，梁正截面开裂弯矩主要由ECC的初裂拉应变决定。当FRP筋-ECC梁进入带裂缝工作阶段后，配筋率对梁弯矩-曲率关系曲线的影响十分明显。随着配筋率的增加，弯矩-曲率关系曲线的斜率逐渐增大，梁的刚度也明显增大。此外，对比不同破坏类型的试件的曲线可以看出，受压破坏的梁配筋率越大，极限曲率越小。由图14(b)可知，梁的极限承载力随着配筋率的增加而逐渐增大。然而，承载力增大速率随着配筋率的增加而逐步降低。

5 延性分析

5.1 延性系数的定义

综合考虑梁的承载能力与变形能力，参考文献[15]中FRP筋混凝土结构的延性指标，定义FRP筋-ECC梁的延性系数Z为

(18)

式中：Md为设计状态下的弯矩；φu为极限曲率；φd为设计状态下的曲率。

对于受拉破坏的梁，当FRP筋拉应变达到极限拉应变的75%时为试件的设计状态。对于受压破坏的梁，设计状态定义为：受压区边缘ECC的压应变达到极限压应变的75%。

5.2 计算结果

基于本文提出的模型，对不同ECC抗压强度和不同配筋率的FRP筋-ECC梁的延性系数进行了数值计算。根据计算结果，分析了不同破坏模式下ECC抗压强度和配筋率对梁延性的影响。

根据破坏类型不同，将试件分为A，B两组。试件编号见表1，其中，A表示受拉破坏，B表示受压破坏，字母后的数字为抗压强度，抗压强度后的数字代表配筋率。各试件的配筋率与延性系数如表2及图15所示。

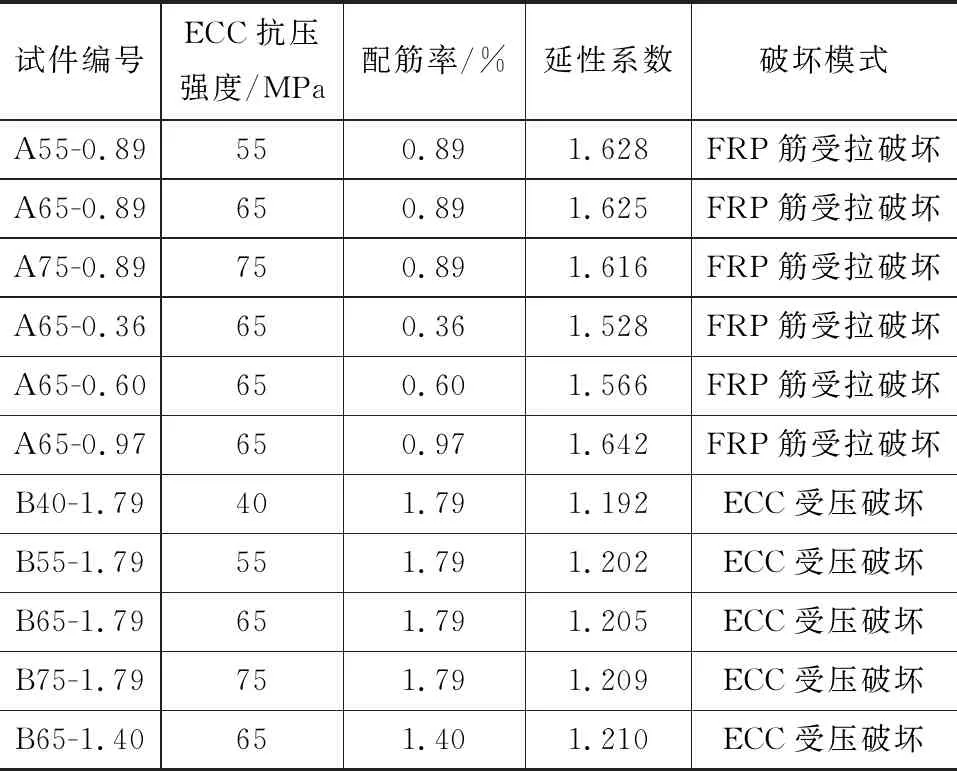
表2FRP筋-ECC梁的延性系数Tab.2Ductility Index of FRP-ECC Beams

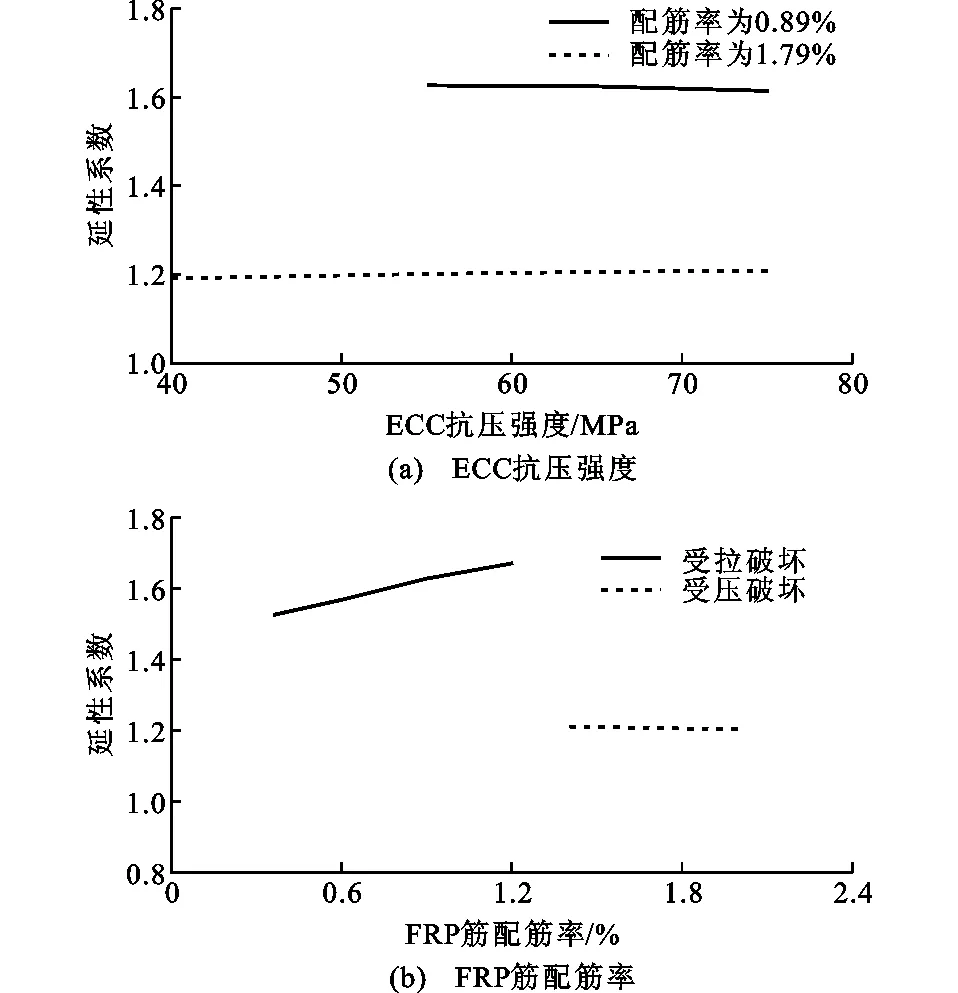
图15延性系数影响因素分析Fig.15Analysis on Influence Factors of Ductility Index

由图15(a)可知，配筋率相同的FRP筋-ECC梁发生FRP筋受拉破坏时(如配筋率0.89%)，随着ECC抗压强度的提高，梁的延性系数略有下降。此时，ECC的强度均未充分发挥，故对其延性影响较小。配筋率相同的FRP筋-ECC梁发生ECC受压破坏(如配筋率1.79%)时，随着ECC抗压强度的提高，梁的延性系数有所上升。这是由于破坏时FRP筋未达到极限抗拉强度，梁发生ECC受压破坏，梁的延性系数取决于ECC的抗压强度，从而随着ECC抗压强度的提高，梁的延性系数有所增大。

由图15(b)可知，ECC抗压强度相同的FRP筋-ECC梁发生FRP筋受拉破坏时，随着FRP筋配筋率的增大，梁的延性系数逐渐增加。ECC抗压强度相同的FRP筋-ECC梁发生ECC受压破坏时，随着FRP筋配筋率的增大，梁的延性系数略有降低。这是由于梁发生ECC受压破坏时，受拉区FRP筋仍未达到其极限抗拉强度，随着配筋率的提高，单根FRP筋承担的拉力减小，由于FRP筋的线弹性特征，单根FRP筋的变形减小，从而随着配筋率的增加，梁的延性系数略有降低。