一种层次聚类和自适应加权K近邻组合的室内定位算法

翟俊杰，李廷会，黄飞江,，袁海波，张虹，胡传君,3

一种层次聚类和自适应加权K近邻组合的室内定位算法

翟俊杰1,2,3，李廷会1，黄飞江1,2,3,*，袁海波4，张虹4，胡传君1,3

（1.广西师范大学 电子工程学院，桂林 541004；2.广州航海学院 信息与通信工程学院，广州 510725；3. 长沙学院 电子信息与电气工程学院，长沙 410022；4. 中国科学院 国家授时中心，西安 710600）

针对基于接收信号强度的位置指纹室内定位算法定位精度不高的问题，提出了一种均值层次聚类和自适应加权K近邻（weighted K nearest neighbor，WKNN）的室内定位算法。算法首先在设置的参考点上采集蓝牙信号强度构建离线指纹数据库，然后采用均值层次聚类方法将所有参考点根据各自之间的相似度分为个类，滤除掉相似度较小的参考点，最后根据待定位点和参考点间的信号距离的相似度，计算出距离差的标准差来自适应确定值，并进行位置估算。实验结果表明，本文提出的算法在定位精度上比WKNN、动态加权K近邻（enhanced weighted K nearest neighbor，EWKNN）方法分别提升了30.0% 和18.0%，在定位实时性上比WKNN和EWKNN方法分别提高了19.2%和28.4%。将该算法用于室内物体定位，可以同时提高定位精度和定位实时性。

室内定位；接收信号强度；指纹数据库；均值层次聚类；自适应加权K近邻

0 引言

随着互联网不断发展，人们对基于位置的服务（location-based sevice，LBS）的需求越来越大，全球定位系统[1]（Global Positioning System，GPS）和北斗卫星导航系统[2-4]（BeiDou Navigation Satellite System，BDS）作为应用最广泛的室外定位技术，由于其信号容易被城市中高楼、隧道等障碍物遮挡，导致全球卫星导航系统（Global Navigation Satellite System，GNSS）在某些室内环境下无法实现定位，为此需要研究室内定位技术。目前主流的室内定位技术主要有射频识别技术[5]（radio frequency identification，RFID）、超带宽技术[6]（ultra-wide bandwidth，UWB）、Wi-Fi[7]和蓝牙技术[8]等。蓝牙有低功耗、低成本、体积小、易于部署和信号强等优点，而且现有的手持移动设备都可以接收到蓝牙信号，使得基于接收信号强度（received signal strength，RSS）的蓝牙室内定位技术得到了广泛的应用[9]。基于RSS的室内定位方法分为基于传播模型[10]和基于位置指纹定位法[11]，由于室内结构复杂，构造出的室内传播模型可能不够准确，而与传播模型方法相比，对位置指纹定位法的研究更为广泛。

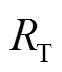
位置指纹算法在室内定位离线阶段时需要在实验区域划分出参考点，导致在某些大型室内环境参考点分布密集，数据量非常庞大。为了对参考点进行筛选，滤除误差较大的点，从而减少定位时间，已有学者将聚类方法应用在位置指纹算法中。文献[15]提出一种基于K-means的加权KNN算法，通过K-means聚类处理指纹数据库，然后在KNN算法中加入加权因子进行匹配，实验表明使用普通KNN算法的平均误差为3.11 m，在使用了K-means的加权改进算法后，能有效提升40%的定位准确度。K-means算法的缺点是K-means容易陷入局部最优，这跟初始给定的中心值有关，所以要尝试多个初始值。文献[16]提出了改进的K-means算法来解决这个问题，但是也需要事先给出聚类的数目，而这个往往难以判断；如果用户选择了不正确的聚类数目，会使本应该在同一个类的数据被判定为两个大的类别，最终影响定位准确度。文献[17]提出了使用基于层次聚类中的最大距离法和改进的KNN算法相结合，实验结果表明改进后算法的平均误差为2.09 m，最大误差为8.25 m，最小误差为0.13 m。与K-means-KNN算法相比，改进后的算法定位准确度更高。但最大距离法以分布在两个类中最不相似的样本（距离最远）作为度量标准进行聚类的方法不够严谨，对离群点的数据比较敏感，降低了指纹数据库分类的准确度，导致最终的定位准确度不高。

针对以上问题，本文提出了基于均值（mean-link，ML）层次聚类和自适应WKNN组合的定位算法。在离线阶段通过ML层次聚类处理数据库中的参考点，降低搜索范围，减少了定位时间，也排除了在线阶段的错误匹配点。在线匹配阶段通过求待定位点与参考点的距离集合的标准差来自适应选择值进行位置估计，提高了定位准确度，减少了定位时间。

1 位置指纹定位算法的原理

位置指纹定位包括离线阶段和在线阶段，指纹定位算法原理如图1所示。

图1 位置指纹定位算法原理图

离线阶段：在实验区域内划分好参考点，在每一个参考点上进行蓝牙信号强度的采集，并记录对应的参考点坐标，记录格式为

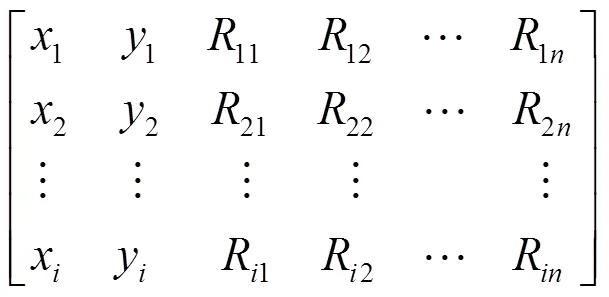
在线阶段：用户进入实验区域内的某一位置，将接收到的蓝牙AP信号强度记录下来，将其与指纹数据库中的信号强度进行搜寻，寻找最佳的匹配点，并使用定位匹配算法计算出估计位置坐标。常见的匹配算法包括KNN，WKNN，贝叶斯分类算法等。

2 层次聚类算法原理

层次聚类分为凝聚和分裂两种聚类方法，凝聚算法是自下而上的算法，分裂聚类算法是自上而下的算法，凝聚和分裂两种方法在本质上是一致的，两种聚类的每一次迭代都是通过某种特定的规则来作为指标，根据不同的数据分布情况来选择对应的层次聚类算法。凝聚的层次聚类，开始时将每一个样本都视为一个类，通过计算每个类之间的距离，按照具体的合并规则将类进行合并，最终将所有类聚类为一个大类或者达到特定的条件则终止聚类。分裂聚类则与凝聚相反，将一个大类逐步分为一个个小类，直到达到终止条件结束聚类。层次聚类的优势在于它的灵活性，不需要事先指定类的数量，通过加入阈值判断，可以很好地控制得到想要的聚类结果。并且层次聚类可以很清晰地展现出样本的划分过程。层次聚类根据聚类条件不同分为最小距离也称单连接算法（single-link，SL）、最大距离也称全连接算法（complete-link，CL）、均值距离（mean-link，ML）和平均距离（average-link，AL）等几种方法[18]。

本文采用的ML层次聚类属于凝聚层次聚类，将离线阶段的每一个参考点视为不同的类，通过合并规则对参考点进行凝聚，直到达到终止条件停止凝聚。最小距离法和最大距离法使用类间最小距离和类间最大距离作为聚类标准不够严谨，对离群点比较敏感，会过于关注局域连接，应用在室内定位中，聚类结果无法达到预期效果。而采用均值或平均距离聚类法对数据库进行聚类，可以解决算法对离群点过于敏感的问题，但是平均距离法计算量较大，每次聚类都需要计算类与类包含的所有数据点间相互的欧式距离，所以采用ML层次聚类，更加契合室内定位的场景。

离线阶段ML层次聚类算法步骤如下[19]：

① 在实验区域选取参考点，采集蓝牙信号，建立信号指纹数据库，计算出所有参考点两两之间的欧氏距离：

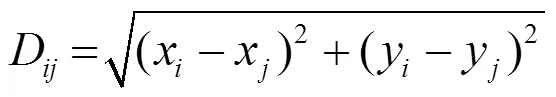
② 计算完成后开始聚类，每一次迭代将欧式距离最小的两个类合并成一个新的类，并计算出新类的中心点。当类与类之间的中心点距离大于阈值时，停止合并。

③ 聚类结束后，计算所有类中心的信号强度：

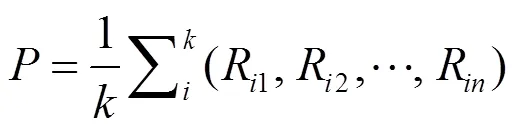
3 基于ML层次聚类和自适应WKNN的定位算法

由于蓝牙信号强度之间的相似度和欧式距离这个特征量相关，所以本文利用欧式距离这个特征向量来反映出待定位点与参考点之间的相似度，并分别应用在室内定位的离线和在线阶段。在空间中，根据信号衰减模型可知，移动终端接收到的蓝牙信号强度与移动终端和蓝牙AP节点之间的距离成正比，两个相邻的参考点如果距离越近，他们采集到的信号强度之间的相似度就越大。根据这个特性，对指纹数据库进行ML层次聚类，可以将在同一区域内，相似度很高的参考点划分为同一个类。由于蓝牙信号有时不稳定，会导致相距很远的参考点之间具有相似的信号强度。针对这个问题，ML层次聚类根据数据库中各参考点之间的欧氏距离对数据库进行区域划分，可以将异常数据排除掉，避免了在线匹配阶段待定位点需要和实际偏远的参考点进行匹配。对数据库进行ML层次聚类后，可以使待定位点直接寻找与自己相似度最高的类进行比较，节省了定位时间，也提高了定位准确度。

自适应WKNN算法是在ML层次聚类的基础上，根据待定位点与参考点之间的信号距离差的标准差来自适应调整值。在实际的定位空间中，存在狭窄区域，也有宽敞的区域，对于不同面积的定位区域，所设定的参考点数量也不同，若每一次定位都选取固定的值，可能会引入相似度很小的参考点，定位的结果将会带来很大误差。本文算法对于每一个不同的待定位点，都会在ML层次聚类的结果上选取相似度最高的类进行匹配，滤除掉误差点，进而选取最优值，提高定位准确度。自适应WKNN算法是在ML层次聚类对数据库处理的基础上进行位置估计，具体实施步骤如下：

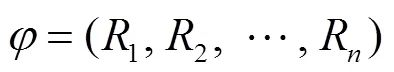
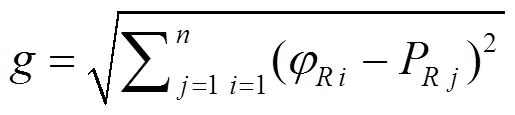
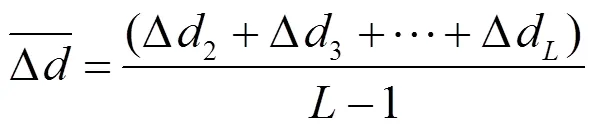
式（6）中，为参考点的个数。

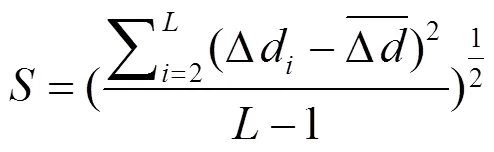
④ 对剩余的个参考点使用WKNN算法进行位置估计：

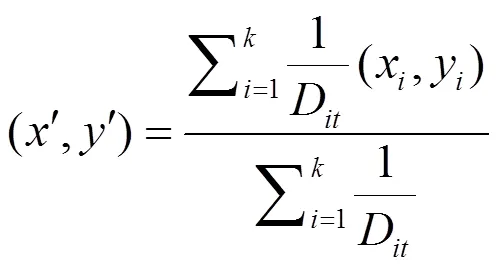
基于ML层次聚类和自适应WKNN定位算法流程如图2所示。

图2 ML层次聚类和自适应WKNN定位算法流程图

基于ML层次聚类和自适应WKNN定位算法详细流程如下：

① 通过式（3）计算数据库中参考点两两之间的欧氏距离，每一次聚类将距离最小的两个点进行合并，每一次聚类都自动更新类的中心。设置阈值，当两个类之间的中心距离大于时，聚类停止；

② 聚类结束后，根据式（4）计算所有类中心的信号强度，用于在线阶段的快速匹配；

③ 在线阶段，采集待定位点的蓝牙信号强度，通过式（5）寻找到离待定位点最近的类C；

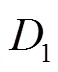
⑤ 根据算出的平均值来通过式（7）进一步求出标准差，滤除掉大于标准差的参考点，最终筛选出值，自适应的选取值，并通过式（8）来得出位置估计。

4 实验和结果分析

为了验证本文提出算法的定位性能，对ML层次聚类和自适应WKNN组合的定位算法、EWKNN算法与WKNN算法进行定位实验比较。

4.1 实验环境

实验选择在学院理工楼4楼进行，如图3所示。图中的标记点为离线指纹数据库中的部分参考点，参考点之间间隔1m，使用华为手机利用该楼层安置的蓝牙iBeacon设备进行数据采集。使用采集的260个参考点构建指纹数据库，每个参考点采集40次，东南西北方向各10次（蓝牙信号强度会受室内人体走动或受静态环境的影响，造成信号波动，这么做是为了避免身体遮挡对信号的影响），每一秒采集一次，取平均值以及对应的，坐标（以图3中的实心点为原点建立直角坐标系）进行储存。在实验区域内随机选择了40个测试点（每个测试点也采集40次，东西南北方向各10次，每秒采集一次，取平均值以及对应的，坐标进行储存）作为在线定位实验样本。

图3 实验区域平面图以及部分参考点划分位置

4.2 实验结果分析

ML层次聚类中阈值的选择决定了聚类效果的好坏，将会影响最终的定位准确度。本文选取了值为7，8，9，10，11，12来进行实验对比，图4为提出的ML层次聚类和自适应WKNN算法对阈值的取值进行的实验结果。

图4 阈值T不同取值的定位平均误差对比

由图4所得，当值取7，8，9，10，11，12时，定位平均误差分别为2.22，1.79，1.66，1.60，1.68和1.73 m，表明的值取7，8，9，10时，定位准确度逐渐提高，且= 10时，定位准确度达到最高。当取11，12时，定位准确度又逐渐下降，所以后面实验的值选择为10。

为了验证算法的定位性能，实验使用相同的指纹数据库和测试集，分别对提出的算法、WKNN和EWKNN定位算法进行定位实验。从平均定位误差，累积定位误差，单点定位误差、最大和最小定位误差、标准差和算法运行时间等方面来分析算法的定位性能。

图5为本文所提出的ML层次聚类和自适应WKNN定位算法和其他两种定位方法的平均定位误差柱状图。由图5可知，ML层次聚类和自适应WKNN定位算法的最终平均定位误差为1.60m，EWKNN平均定位误差为1.95m，而WKNN平均定位误差则为2.29m，提出的算法在定位准确度上和WKNN、EWKNN相比分别提高了30.0％和18.0％。

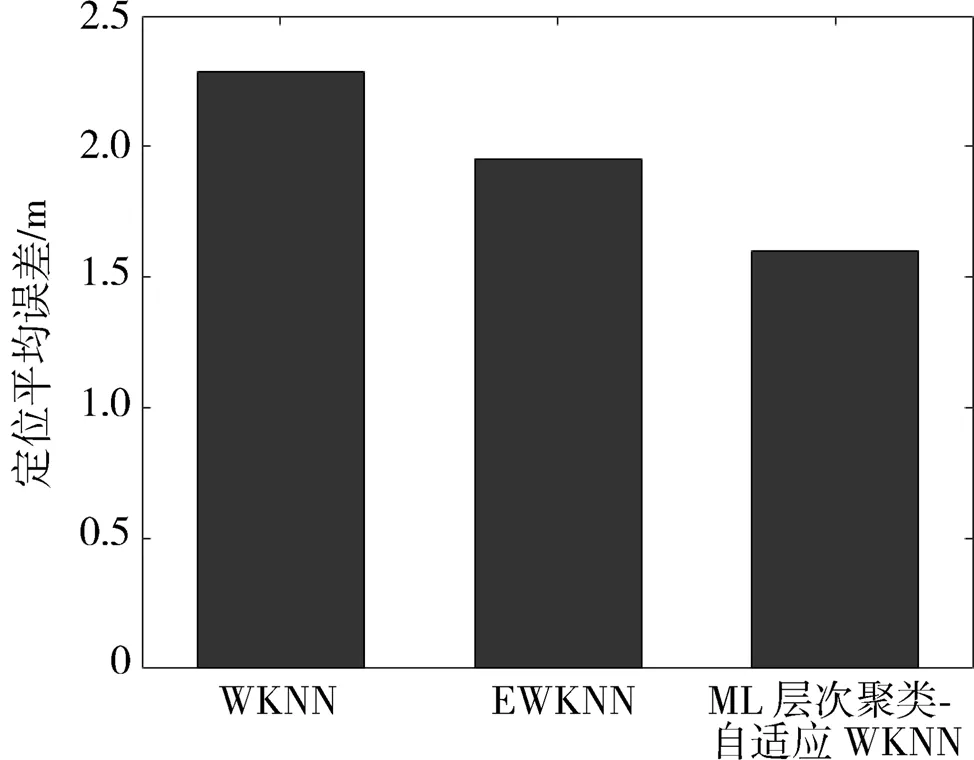
图5 3种定位算法的平均定位误差

ML层次聚类和自适应WKNN定位算法与其他两种算法的累积定位误差分布概率如图6所示，将误差分布概率数据呈现在表1中。从图6和表1可以观察出各种算法的定位准确度的趋势，从图6中可以发现本文提出的ML层次聚类和自适应WKNN定位算法定位误差在1.5 m内达到了67.5％，在定位准确度上较其他两种定位算法有很大的提升。ML层次聚类和自适应WKNN定位算法的定位误差在2 m以内达到了77.5％，定位成功率在2.5 m以内达到了90％。综上所述，本文提出的定位算法在平均定位误差和累积定位误差上都要优于其他两种算法。

图6 累积定位误差分析

表1 3种算法定位结果对比

对40个待定位点使用ML层次聚类-自适应WKNN算法与WKNN，EWKNN算法进行位置估计，每一个待定位点的定位误差比较如图7所示，定位误差的最大、最小误差、定位平均误差、标准差统计如表2所示。由图7和表2可知，ML层次聚类-自适应WKNN算法的最大误差距离为3.48 m，EWKNN算法的最大误差距离为4.06 m，提出的算法最小误差也比EWKNN算法要小。从图7可以看出提出的算法较WKNN和EWKNN算法整体的定位准确度有所提升，而且波动较小，从表2可以看出提出算法的标准差较小，定位的稳定性更好。

图7 3种算法的单点定位误差比较

表2 改进算法与其他两种算法最大、最小误差、定位平均误差和标准差对比

采用Matlab软件对3种定位算法在相同的软硬件环境下分别运行20次仿真，并对算法运算时间进行统计，将20次结果取平均值，得到3种定位算法的平均运算时间如表3所示。ML层次聚类和自适应WKNN定位算法由于在离线阶段对指纹数据库进行了聚类处理，减小了在线匹配的范围，降低了在线匹配阶段的运算量，最终运算时间较其他两种算法均有减少。而EWKNN算法在在线匹配阶段由于需要通过计算对值进行选择，并且需要计算测试集与指纹数据库中所有参考点之间的欧氏距离，大大增加了计算量，所以运算时间较WKNN算法有所增加。WKNN虽然运算时间和EWKNN算法相比有所降低，但传统的WKNN算法对每一个待定位点都选取相同的值进行定位匹配，导致定位准确度不高。综上所述和其他两种算法相比，本文提出的ML层次聚类和自适应WKNN定位算法在定位准确度有了提高，在算法平均运算时间上有减小。

表3 3种算法平均运算时间比较

5 结语

针对WKNN算法采用固定的值，EWKNN算法需要调整阈值来动态确定值而导致的定位时间长、定位准确度低等问题，提出了基于ML层次聚类和自适应WKNN的组合定位算法。算法先通过层次聚类，缩小在线匹配范围，滤除掉相似度较小的参考点，在线匹配阶段，根据距离集合的标准差来自动筛选值。在学院理工楼4楼进行了定位实验，使用采集的260个参考点构建指纹数据库，并在实验区域内随机选择了40个测试点作为在线定位实验样本。实验结果表明，ML层次聚类和自适应WKNN定位算法的平均定位误差为1.60 m，在定位平均误差上比WKNN算法、EWKNN算法分别降低了30.0%和18.0%。算法的平均运算时间为0.63 s，在运算时间上比WKNN、EWKNN分别降低19.2%和28.4%。本文提出的算法在类似的环境下可以较好地根据各参考点之间的相似度进行聚类划分，在此基础上再进行自适应的在线匹配算法，从而提高定位准确度。另外在位置指纹库数据库的建立上，本文采用的方法是在每一个参考点上多次采集信号强度，如果实验区域较大，那么建立数据库的工作量将会非常大，因此在离线阶段如何快捷准确地构建数据库还需要继续研究，进一步改善定位效果。

[1] ENGE P K. The global positioning system: signals, measurements, and performance[J]. International Journal of Wireless Information Networks, 1994, 1(2): 83-105.

[2] 魏亚静, 袁海波, 董绍武, 等.BDS星钟预报误差分析及对授时性能的影响[J]. 时间频率学报, 2016, 39(4): 301-307.

[3] 肖秋龙, 成芳, 沈朋礼, 等. 北斗地基增强系统观测数据质量分析[J]. 时间频率学报, 2019, 42(3): 266-273.

[4] 武文俊, 广伟, 张继海, 等. 北斗亚欧共视时间比对试验[J]. 时间频率学报, 2018, 41(3): 200-205.

[5] 何静, 刘冉, 肖宇峰, 等. 融合RFID相位差和激光扫描的动态目标定位[J]. 仪器仪表学报, 2018, 39(2): 81-88.

[6] GIGL T, JANSSEN G J M, DIZDAREVIC V, et al. Analysis of a UWB indoor positioning system based on received signal strength[C] // IEEE 2007 4th Workshop on Positioning, Navigation and Communication, Hannover: IEEE, 2007: 97-101.

[7] 李奇越, 李伟, 孙伟, 等. 基于RSSI和辅助节点协作的Wi-Fi室内定位方法[J]. 电子测量与仪器学报, 2016, 30(5): 794-802.

[8] 卞合善. 基于蓝牙4.0低功耗室内定位研究[D]. 北京: 北京邮电大学, 2015.

[9] 张凯楠. 低功耗蓝牙组网和定位技术研究[D]. 北京: 北京邮电大学, 2018.

[10] ELKAFRAWY K, YOUSSEF M, ELKEYI A, et al. Propagation modeling for accurate indoor WLAN RSS-based localization[C] //IEEE Vehicular Technology Conference(VTC’10),Ottawa: IEEE, 2010.

[11] 夏颖, 马琳, 张中兆, 等. 基于半监督流形学习的WLAN室内定位算法[J]. 系统工程与电子技术, 2014, 36(7): 1422-1427.

[12] 吴泽泰, 蔡仁钦, 徐书燕, 等. 基于K近邻法的WiFi定位研究与改进[J]. 计算机工程, 2017, 43(3): 289-293.

[13] FANG Y Q, DENG Z, XUE C, et al. Application of an improved K nearest neighbor algorithm in WiFi indoor positioning[C]//China Satellite Navigation Conference 2015, Xi’an: Organizing Committee of the 6th China Satellite Navigation Academy Annual Conference, 2015: 517-524.

[14] SHIN B, LEE J H, LEE T, et al. Enhanced weighted K-nearest neighbor algorithm for indoor Wi-Fi positioning systems[C]//2012 8th International Conference on Computing Technology and Information Management, Seoul: IEEE, 2012: 574-577.

[15] 吉彩云, 袁明辉, 李瑞祥, 等. 基于K-means的室内定位加权优化k-NN算法[J]. 电子测量技术, 2018, 41(10): 66-69.

[16] 陈望, 贾振红, 覃锡忠, 等. 基于改进K-means聚类算法的室内WLAN定位研究[J]. 激光杂志, 2014, 35(7): 11-14.

[17] 王怡婷, 郭红. 基于层次聚类的WiFi室内位置指纹定位算法[J]. 福州大学学报(自然科学版), 2017, 45(1): 8-15.

[18] 段明秀. 层次聚类算法的研究及应用[D]. 长沙: 中南大学, 2009.

[19] 常津铭, 王红蕾. 基于层次聚类和贝叶斯的室内定位算法[J]. 计算机时代, 2019(2): 5-8.

An indoor positioning algorithm based on hierarchical clustering and adaptive weighted K nearest neighbor combination

ZHAI Jun-jie1,2,3, LI Ting-hui1, HUANG Fei-jiang1,2,3,*, YUAN Hai-bo4, ZHANG Hong4, HU Chuan-jun1,3

(1. College of Electronic Engineering, Guangxi Normal University, Guilin 541004, China;2. College of Information and Communication Engineering, Guangzhou Maritime University, Guangzhou 510725, China;3. College of Electronic Information and Electrical Engineering, Changsha University, Changsha 410022, China;4. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China)

Aiming at the problem that the location fingerprint indoor positioning algorithm based on received signal strength (RSS) with low positioning precision, this study proposed an indoor positioning algorithm based on mean-linkage (ML) hierarchical clustering and adaptive weighted K nearest neighbor (WKNN) combination. Firstly, the Bluetooth signal strength is collected at the set reference point to construct an offline fingerprint database. Then, using ML hierarchical clustering method, all reference points are divided intocategories according to the similarity between them, and the reference point with less similarity is filtered out. Finally, according to the similarity of the signal distance between the point to be located and the reference point, the standard deviation of the distance difference is calculated to adaptively determine thevalue and perform the position estimation. The experimental results show that the proposed algorithm improves the positioning precision by 30.0% and 18.0% compared with WKNN and EWKNN respectively, and improves the positioning real-time by 19.2% and 28.4% compared with WKNN and EWKNN respectively. The algorithm is applied to indoor object positioning, which can simultaneously improve positioning precision and positioning real-time.

indoor positioning; received signal strength (RSS); fingerprint database; mean-linkage hierarchical clustering; adaptive weighted K nearest neighbor

10.13875/j.issn.1674-0637.2020-04-0300-10

翟俊杰, 李廷会, 黄飞江, 等. 一种层次聚类和自适应加权K近邻组合的室内定位算法[J]. 时间频率学报, 2020, 43(4): 300-309.

2020-05-21；

2020-06-20；

国家自然科学基金资助项目（61964004）；湖南省自然科学基金资助项目（2015JJ2016）；长沙学院“青年英才支持计划”和科研基金资助项目（SF1615）