磁浮列车涡流制动电磁力特性曲线的求解研究*

薛锐锋，倪文波，闫一凡

（1 西南交通大学机械工程学院， 成都610031；2 中车工业研究院有限公司， 北京100071）

磁浮列车以其节能环保、安全性高、噪声低、乘坐平稳舒适等优点，成为轨道交通领域的研究热点[1]。随着国内城市群的发展，200 km/h 速度等级的中速磁悬浮成为解决城际之间快速交通问题的一种技术措施[2]。与高速磁悬浮列车相似[3]，其制动系统采用3 种制动方式:电制动、机械制动、涡流制动，在其发生牵引和电制动系统失效及其他紧急情况下，列车将启动安全制动系统，采用机械制动和涡流制动来共同完成制动过程。

磁浮列车运行控制系统由中央控制系统(CCS)、分区控制系统(DCS)和车载运行控制系统(VCS)3 个子系统组成，当触发安全制动系统时，分区控制系统根据当前运行线路位置、当前运行车速、临时限速、前方停车位置信息等[4]，采用预算法获得列车速度−制动距离曲线，确定出需要实施的涡流制动等级和切换制动等级的位置信息[5]，并将其传输给车载运行控制系统对列车涡流制动装置进行控制。

为使磁浮列车能够准确的停靠在指定的安全停车区，必须对列车安全制动施加的涡流制动力进行精确控制，使列车能够按照预定的制动曲线进行制动。但即使涡流制动装置结构和基本参数一定，列车安全制动时的电磁力受到运行速度和气隙大小的影响，使精确的涡流制动力求解难以获得。结合安全制动的控制方式，根据涡流制动装置的结构特点，对通过电磁仿真计算得到的离散电磁力数值处理方法进行研究，从而获得安全制动所需的涡流制动电磁力特性曲线。

1 线性涡流制动装置的结构与原理

如图1 所示为某型中速磁浮列车涡流制动装置的结构图，由制动装置框架、励磁电磁铁、磁轭、磨耗板等组成。该装置沿车体前进方向分布多个励磁电磁铁，通过横向和纵向的铰接以及垂向的支撑，使涡流制动装置与悬浮架进行连接，从而实现列车实施制动时涡流制动装置的相对位移变化和力的传递。

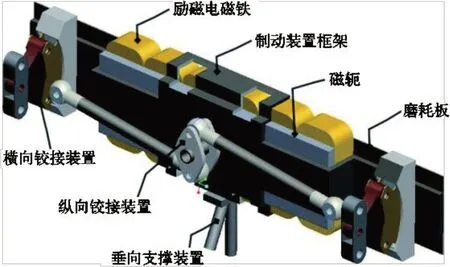
图1 涡流制动装置结构图

安全制动等级根据励磁电流的大小分为0～7 共8个等级，0 级时励磁电流最大，即产生的电磁力最大，7级时励磁电流为0 即关闭涡流制动器。涡流制动器与侧向导轨间相对运行速度小于一定速度值后，通过电磁感应产生的电磁制动力急速减小，因此常在电磁法向吸力的作用下使气隙逐渐减小到磨耗板与侧向导轨贴合，利用法向吸力使磨耗板与侧向导轨产生压力而产生滑动摩擦力来弥补电磁制动力的减小，两个力的合力即为涡流制动过程中对列车施加的制动力[5]。

涡流制动装置通过两个横向球铰结构与构架相连，其横向球铰结构如图2 所示，由三角形连接板、球铰和两个预紧的弹簧组成，使得列车正常运行时气隙值d保持最大气隙dmax，实施安全制动时可通过预紧弹簧的压缩变形使气隙发生变化，在磨耗板与侧向导轨贴合时气隙值为最小dmin，即为磨耗板的厚度。

图2 横向连接装置结构简图

由涡流制动装置的结构可知，此装置在横向上共有4 个预紧弹簧。预紧弹簧的压缩位移为x′，涡流制动装置的横向位移为x，在x变形属于范围[0，dmax−dmin]内时，x与x′的关系式为:

式中α表示预紧弹簧中心线与涡流制动装置横向间的夹角。

涡流制动装置在横向上所受的弹簧力Fa与单个预紧弹簧的弹力F′的关系式为:

对单个预紧力为Fyujin、弹性刚度为k′的预紧弹簧，弹性应变x′与弹力F′的关系式为:

由式（1）～式（3）可得涡流制动装置的横向位移x与Fa的关系式为:

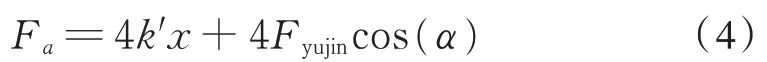
由式（4）可得，涡流制动装置的横向位移x与预紧弹簧产生的横向合力Fa呈线性变化关系，其横向铰接刚度k为定值 4k′，横向预紧力为 4Fyujincos(α)。在预紧弹簧初始预紧力Fyujin和其弹性刚度k′的结构参数值一定时，涡流制动装置在横向上产生最大位移即气隙变为最小时的横向力F1和开始产生位移即气隙开始变化对应的横向力F2的值也是一定的。列车在开始实施安全制动后，当法向吸力F大于F2后励磁电磁铁与侧向导轨间的气隙值从dmax开始减小，直到大于或等于F1后气隙缩到最小，使磨耗板与侧向导轨贴合后，气隙大小不再发生变化。

对于不同的制动励磁等级，涡流制动装置产生的法向吸力大小不同，使得F1、F2分别对应的列车运行速度值v1、v2值也各不相同，即使同一制动等级在不同速度下产生的制动电磁力也不同，需要对其变化规律进行相应分析。

2 仿真计算离散数据处理方法

列车实施安全制动过程中，涡流制动装置与侧向导轨之间是一个变气隙、变速度的相对复杂运动过程，使得对列车每一时刻施加的连续安全制动力难以直接求解，从而致使难以对列车进行精确控制。

通常计算安全制动的电磁力主要采用两种方法:解析法求解特性方程和有限元仿真计算法[6−7]，随着计算机技术的提高和有限元方法的成熟，采用有限元软件进行电磁仿真是一种方便快捷准确的方法。但有限元法只能对特定运行工况进行仿真计算，只能获得每一制动等级的多个离散的气隙值−运行速度大小−电磁力的数值点，为了获得每一制动等级时考虑变气隙过程连续的法向吸力和切向制动力曲线，文中采用Hermite 插值法对离散数值进行处理。

2.1 Hermite 插值法

为了使获得的曲线较为光滑，且最大程度保真仿真计算的数值，采用分段3 次Hermite 插值法对数据进行处理。对每个制动等级和气隙值工况，将仿真计算获得的速度—法向吸力和速度—切向制动力数组，在每个速度区间[vk，vk+1]内，拟合电磁力 3 次多项式函数fk(v)；该函数通过仿真值f(vk)和f(vk+1)进行计算，且需要满足相邻区间边界处的一阶导数f′(vk)、f′(vk+1)相等。由此可得其表达式为[8]:

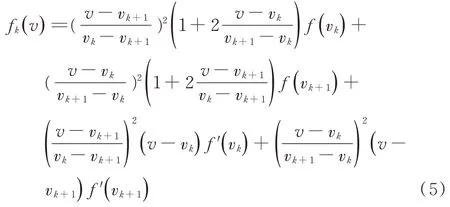
该方法较为成熟，Matlab 已有标准的函数可以调用。通过仿真得到的电磁力离散点数组，调用此插值函数获得每个制动等级，在气隙值分别为最大气隙、中间气隙、最小气隙3 种工况下，对随运行速度变化的切向制动力和法向吸力拟合电磁力曲线。如图3 所示为在施加0 级涡流制动等级时，使用仿真计算得到数值获得单个涡流制动装置的切向制动力和法向吸力曲线。由图可得气隙越小电磁力越大，在同一气隙值下随着运行速度的减小，法向吸力单调增大，切向制动力呈先增大后减小的趋势。其他制动等级也可得类似结果。

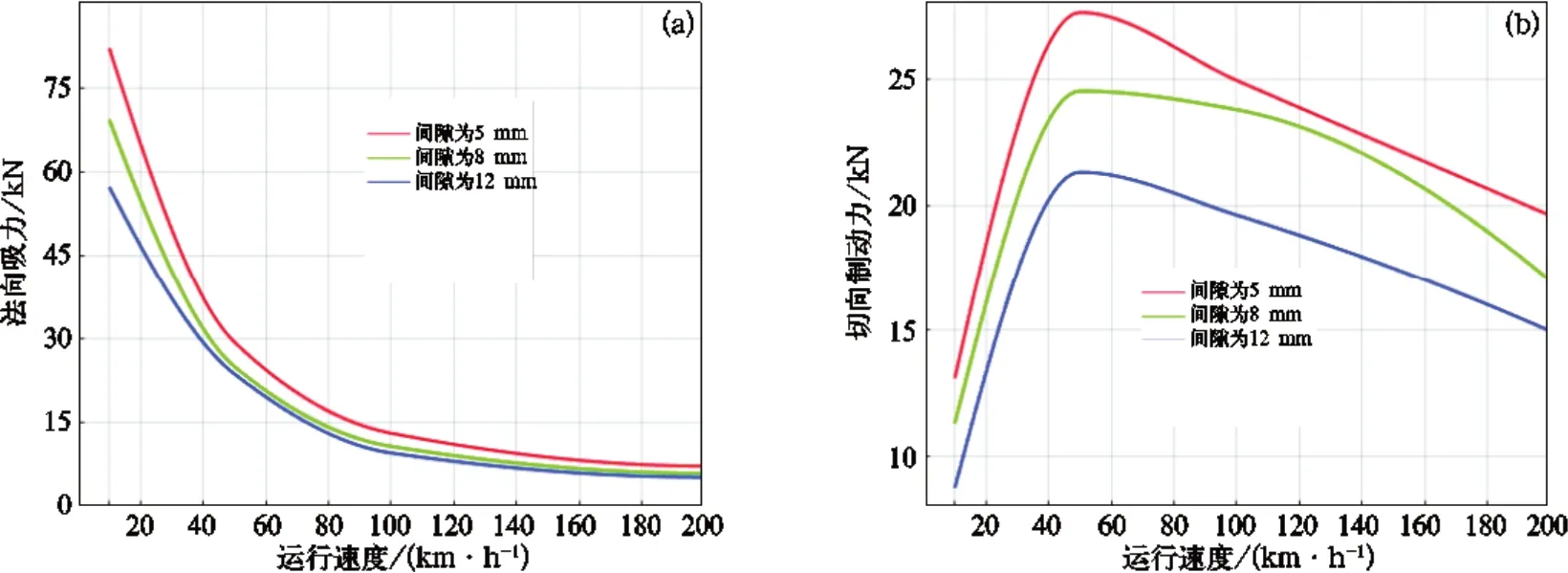
图3 0 级涡流制动等级时3 种气隙情况拟合获得的电磁力曲线

2.2 气隙变化过程分析

由第1 小节推论可得，气隙大小由涡流制动装置横向连接弹簧产生的力和励磁电流产生的法向吸力来决定。将横向连接弹簧产生的定值力F1和F2分别与每一制动等级拟合获得的不同气隙法向吸力曲线进行比对，分两种情况进行分析即可获得气隙变化规律。

(1) 若F1和F2值分别处于气隙最小、最大时的法向电磁力数值范围内，利用法向吸力变化的单调性，使用插值法分别在气隙最小、最大曲线上得到对应的速度点v1和v2的值。结合列车安全制动过程中运行速度范围，分两种情形对气隙变化过程进行讨论。

对v1和v2的大小进行对比，若v1值小于等于v2，如图4(a)所示，列车在实施安全制动过程中，涡流制动装置在初始气隙值下使列车速度降低至v2后，随着法向吸力增大使气隙开始减小，气隙减小又使得法向吸力增大，因而是一个动态的变化过程，直至列车速度降为v1后，气隙值减小为最小值。由此可得运行速度v>v2速度段，气隙值为最大值；v＜v1速度段，气隙值为最小值；在v1＜v＜v2速度段，即为气隙不断变化的过程。由此可得其法向吸力曲线为a-b、c-d段，b-c段变气隙特性曲线下节求解。

若v1值大于v2，如图 4(b)所示，由于v2处对应的最小气隙的法向吸力大于F1的值，可认为在很小的速度范围内使气隙变化为最小值。由此可得运行速度v>v2速度段，气隙值为最大值，v＜v2速度段，气隙值为最小值且保持不变直至结束安全制动，此时其法向吸力曲线为a-b-c-d曲线。

(2) 若F1或F2的值超出气隙最小、最大法向吸力曲线数值范围内时，如图5 所示。在列车安全制动开始时的vmax(v2)处，最大气隙对应的法向吸力值大于F2，如图5(a)所示，涡流制动装置受吸力作用而使气隙快速减小到受力平衡位置，该位置间于[dmin，dmax]之间，a-b制动阶段为变气隙过程；在列车结束安全制动时的vmin(v1)处，最小气隙对应的法向吸力仍小于F1，如图5(b)所示，即此处的气隙值间于[dmin，dmax]之间，磨耗板与侧向导轨到关闭涡流制动装置时还未贴合产生摩擦力，b-c制动阶段为变气隙过程。

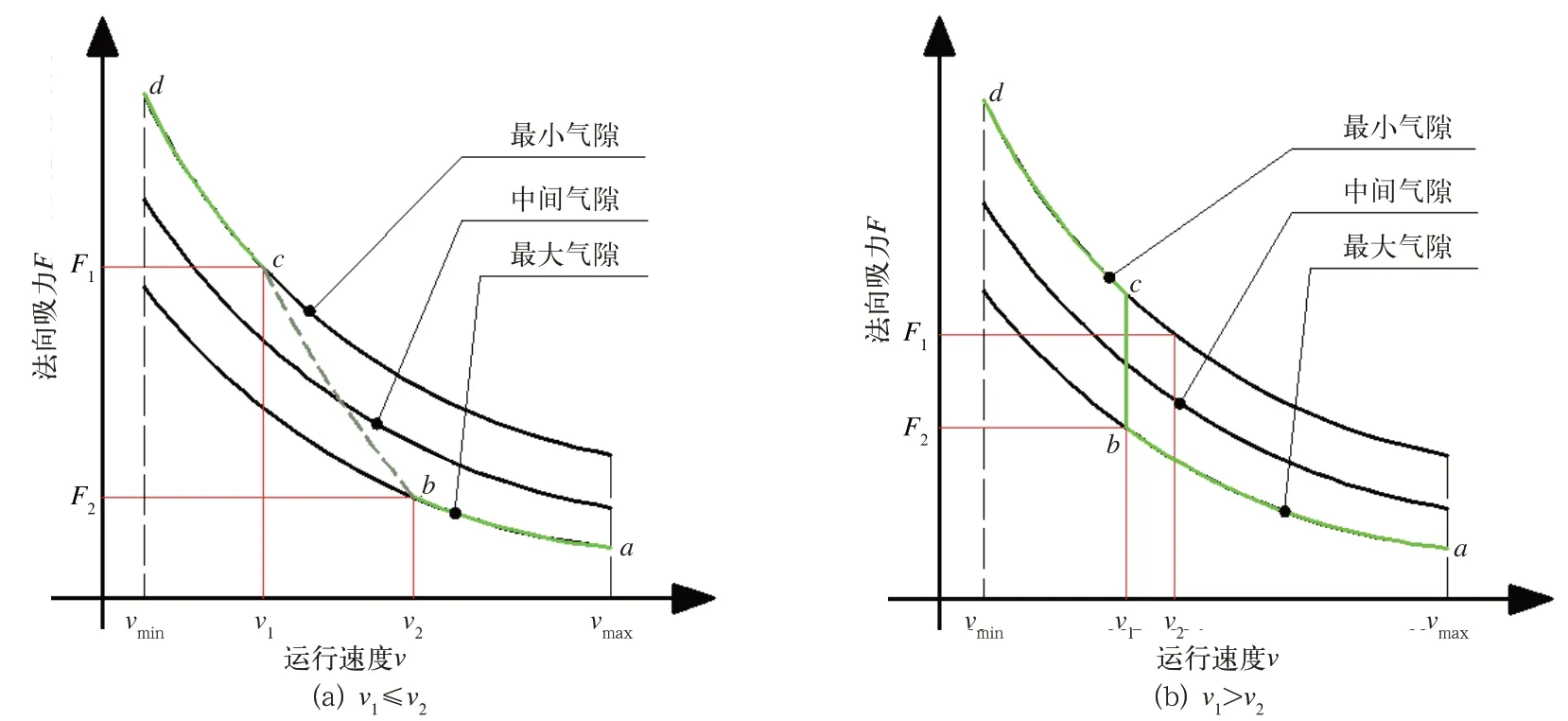
图4 F1 和F2 的值处于对应气隙法向吸力曲线数值范围内

2.3 变气隙阶段特性曲线的求解

在v1～v2速度范围内，气隙值从初始气隙值逐渐缩小为结束时对应的气隙值，是一个动态的变化过程，为求解气隙变化特性曲线，在v1和v2速度范围内通过等间值取一定的速度值点，通过求取这些速度值处稳态的气隙值和法向吸力值，而后将所得数值点进行拟合即可得到连续的考虑变气隙过程的电磁力曲线。

对于气隙的变化过程，因涡流制动装置在横向采用有预紧的弹性铰接装置，使气隙值的大小与法向吸力呈一定的线性变化关系，如图6 所示，斜率为该涡流制动装置的铰接刚度k。由此可得法向吸力F与气隙值d的函数关系式为:

由拟合获得的3 条不同气隙工况的电磁力曲线，利用插值法可得在每个速度点处的3 组不同气隙下的法向吸力数值，拟合为法向吸力与气隙值d的二阶多项式函数:

联合式（6）和式（7）进行求解，即可获得速度值v处气隙相对稳定时的值为d。从而通过计算获得变气隙过程对应速度点处的法向吸力和切向制动力。由插值速度点和所得电磁力数值，采用分段3 次Hermite 插值法拟合得到变气隙过程的法向吸力特性曲线，与前面得到的v＜v1与v>v2速度段特性曲线组合得到该制动等级下总的法向吸力特性曲线。

图6 涡流制动装置所受法向吸力与气隙值的关系曲线

同理，将拟合的切向制动力曲线对应的速度段分段，根据已经获得的各特征速度点处的气隙值，利用插值法得到对应的切向制动力数值，并拟合得到变气隙过程的切向制动力特性曲线。

3 电磁特性曲线求解

通过以上分析，定义合理的F1和F2数值，通过Matlab 编译程序，即可对某磁浮列车涡流制动装置的电磁特性仿真数值进行处理，从而获得如图7 所示的各励磁电流值下的运行速度−气隙值、运行速度−切向制动力和运行速度−法向吸力拟合曲线。

如图7(a)所示为拟合获得的各制动等级在安全制动过程中的气隙变化过程，由图可得在涡流制动为0 级时，在开始制动的200 km/h 处气隙值为11.2 mm，在速度值为140 km/h 处气隙值减小为最小值；在涡流制动等级为6 级时，气隙一直保持最大值至23 km/h，然后开始变小，直至涡流制动结束时即运行速度为10 km/h，气隙减小为5.6 mm，仍未减为最小。

图7 数据处理所得拟合曲线结果

图7(b)所示为各励磁等级对应的法向吸力随列车运行速度变化的连续曲线，图7(c)为各励磁等级对应的切向制动力随运行速度变化的连续曲线。

4 结束语

安全制动系统是磁浮列车安全运行极其重要的组成部分，因而具有重要的研究意义。结合线性涡流制动装置的结构特性，对采用有限元法计算获得的离散电磁力数值，通过3 次Hermite 插值法获得不同气隙值对应的电磁力曲线，而后根据列车涡流制动过程中气隙的变化规律，获得了各制动等级考虑变气隙过程的电磁力特性曲线，可为磁浮列车安全制动过程中线性涡流制动装置产生的涡流电磁力的求解提供一种数值处理方法。