基于SIMPACK 的轨道工程车辆动力学仿真及优化分析

杨茜茜

（中国铁建高新装备股份有限公司，昆明650215）

某型轨道工程车连挂速度为120 km/h，按照相关的标准规范，该型轨道工程车的动力学性能试验速度应不低于132 km/h。

该工程车进行动力学试验过程中，运行速度达到125 km/h 时，横向振动有蛇行失稳的趋势，横向加速度和横向平稳性指标超过限度值。对试验数据进一步分析，发现车辆纵向定位刚度不足且摩擦阻尼匹配不合理，横向临界速度偏低。

为了提高该车辆的抗蛇行失稳的临界速度及车辆运行平稳性，通过SIMPACK 建立车辆动力学仿真模型，优化相关参数，对车辆的动力学性能进行计算评估，并通过动力性性能试验加以验证。

1 车辆主要构成及主要计算参数

1.1 车辆模型特点

该型轨道工程车为四轴车，其走行部由2 台二轴转向架组成。前转向架为驱动转向架，后转向架为从动转向架。前、后转向架的结构基本相同，均由转向架构架、轮对轴箱装置、球面心盘总成、常接触弹性旁承、弹簧减振装置、基础制动装置等部分组成。转向架均采用H 形整体焊接构架，主要由两根侧梁和一根横梁组成，侧梁和横梁均为变截面的封闭箱形断面，这种设计重量轻强度高，且能提供较大的抗菱刚度。弹簧减振装置由螺旋钢弹簧、斜楔式变摩擦减振器等组成。其轴箱采用导框定位式结构，横向有定位间隙，纵向为准刚性定位。车体全部质量均通过球面心盘和两侧常接触旁承，坐落在构架上，并通过一系悬挂作用在轴箱和轮对上。

1.2 车辆主要计算参数

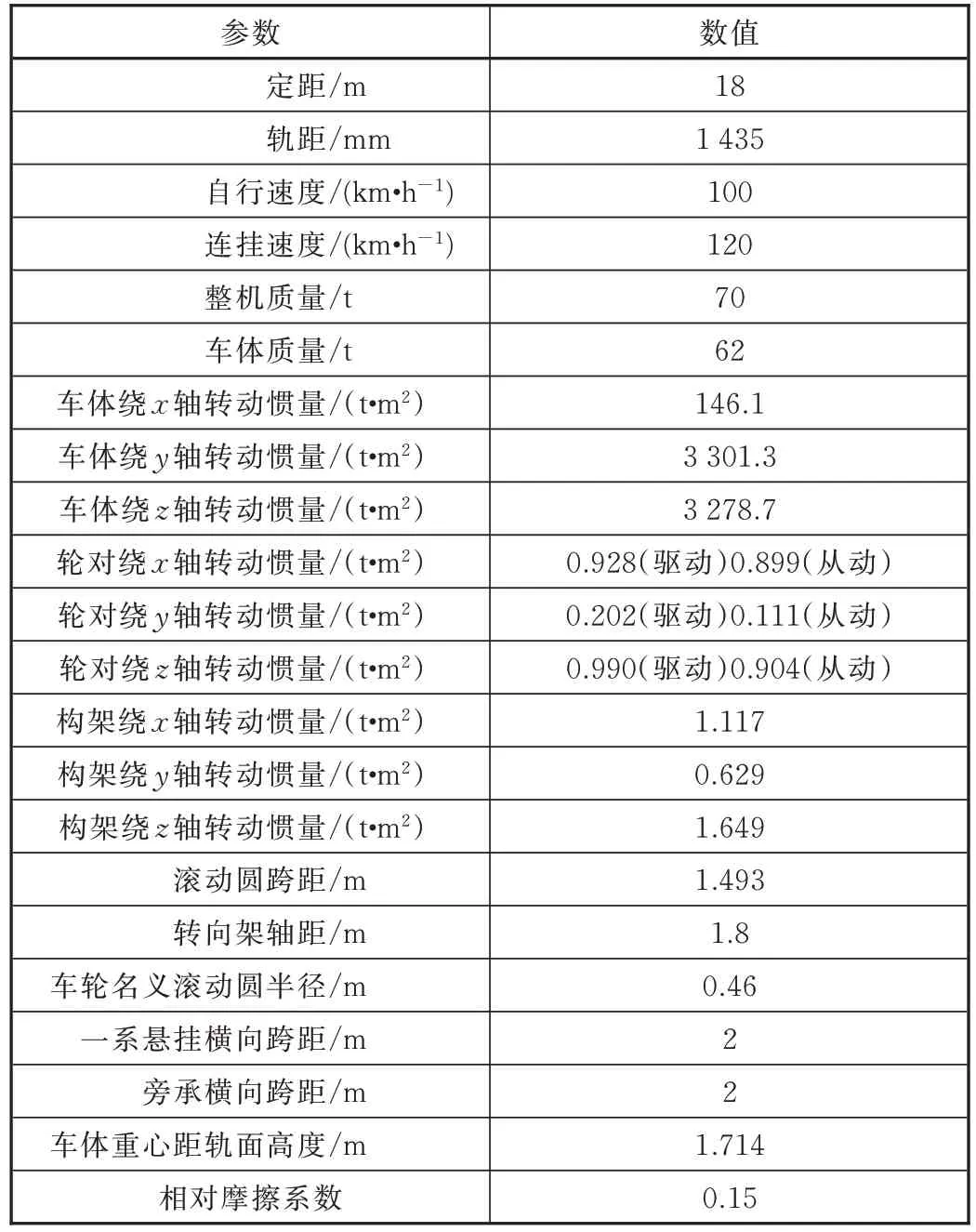
表1 车辆主要计算参数

2 车辆动力学模型

模型由 1 个车体、2 个构架、4 个轮对和 8 个轴箱共15 个刚体组成。由于考虑车辆是匀速运动，因此可以不考虑各刚体沿x轴方向的平行移动（伸缩），转向架构架的横移位移、浮沉位移与车体的横移、浮沉、点头、摇头和侧滚位移相关，不是独立的自由度，轮对的浮沉、侧滚运动是轮对横移和摇头角的函数，因此不是独立的自由度，轴箱相对于轮对有点头运动，其他运动方式和轮对一致。在仿真分析中车辆各刚体的广义坐标如表2所示。

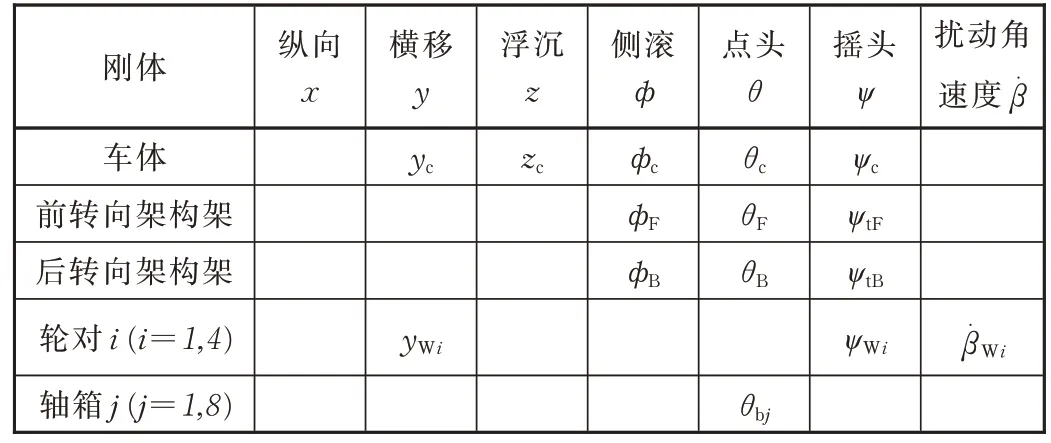
表2 车辆动力学模型自由度

根据该型轨道工程车结构特点，在建立动力学模型时，车体、轮对、构架和轴箱等部件均视为刚体，忽略钢轨的弹性变形。同时考虑了各种非线性的关系，主要包括非线性轮轨接触关系、非线性轮轨力和非线性悬挂力。结合车辆动力学计算参数和车辆动力学模型自由度，动力学计算模型如图1 所示。

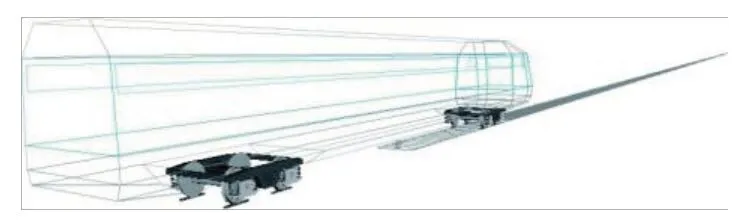
图1 车辆动力学模型

根据转向架的结构特点，变摩擦减振的模拟采用相对摩擦系数斜楔建模方法。该方法主要考虑斜楔垂向自由度，仅在纵垂面上分析斜楔受力。由于斜楔摩擦减振器在纵向位移量小，所以副摩擦面上摩擦力做功远小于主摩擦面，因此在摩擦阻力计算时仅考虑主摩擦面的摩擦力。通过斜楔受力平衡分析得出，斜楔向下运动主摩擦面摩擦力f下和向上运动主摩擦面摩擦力f上，，如图2所示。

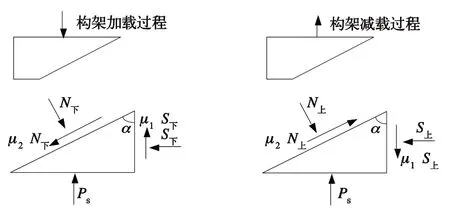
图2 斜楔受力分析示意图

相对摩擦系数所表达的是斜楔在一个上下运动循环内摩擦功所占系统机械能比例，并由其衡量斜楔摩擦减振器的减振性能。在进行动力学仿真计算时，将斜楔摩擦减振器产生的摩擦力以平均相对摩擦系数与斜楔所受垂向弹簧反力的乘积表示。

3 计算结果优化及分析

依据GB/T 17426−1998《铁道特种车辆和轨行机械动力学性能评定方法和试验方法》（以下简称“标准”），动力学性能仿真分析计算主要指标包括：

（1）稳定性指标:车辆蛇行运动稳定性的临界速度；

（2）平稳性指标:车辆在直线上运行时的横向和垂向平稳性指标，横向及垂向最大加速度；

（3）安全性指标:车辆通过曲线时的轮轴横向力、脱轨系数、轮重减载率和倾覆系数。

3.1 稳定性分析

对于非线性的车辆系统，通过观察车辆系统各刚体的振动情况来判定车辆系统的蛇行稳定性。蛇行运动伴随车辆运行一直存在，一般在受到激扰后能很快收敛到平衡位置[1]。本模型临界速度的计算方法为:给定一段有限长的实际轨道随机不平顺激扰样本函数，首先让列车运行在不平顺轨道上并激发其振动，然后让列车运行在理想光滑轨道上，通过分析车辆在不同的运行速度下各刚体振动位移随时间的变化情况，来判断系统是否出现蛇行失稳。根据此方法得出斜楔主摩擦面摩擦系数与蛇行运动失稳临界速度的关系如表3 所示。

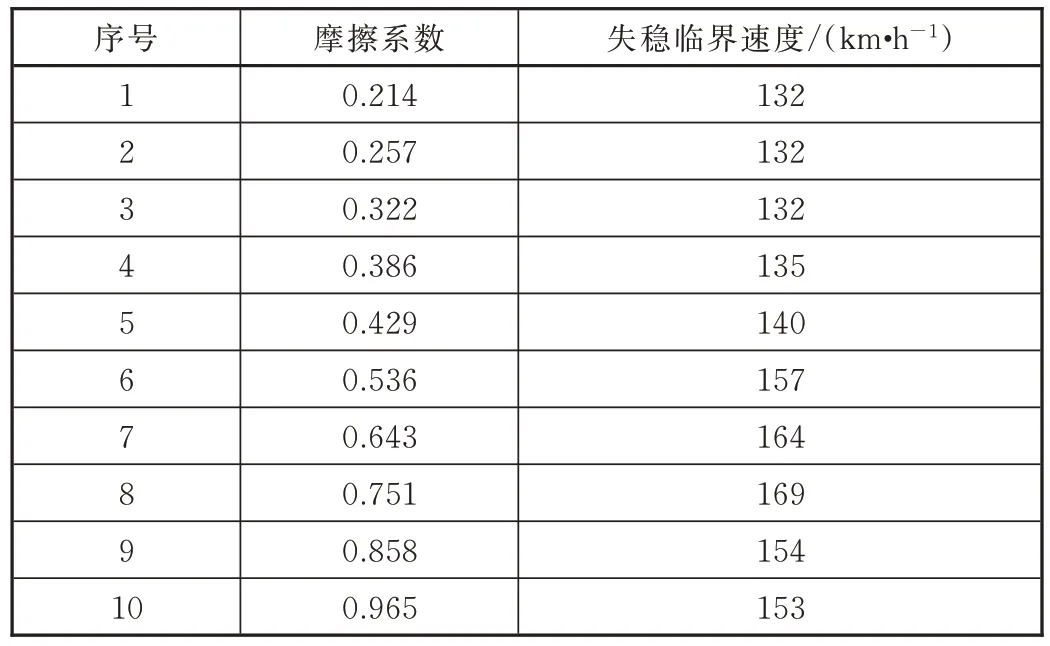
表3 摩擦系数与蛇行运动失稳临界速度的关系

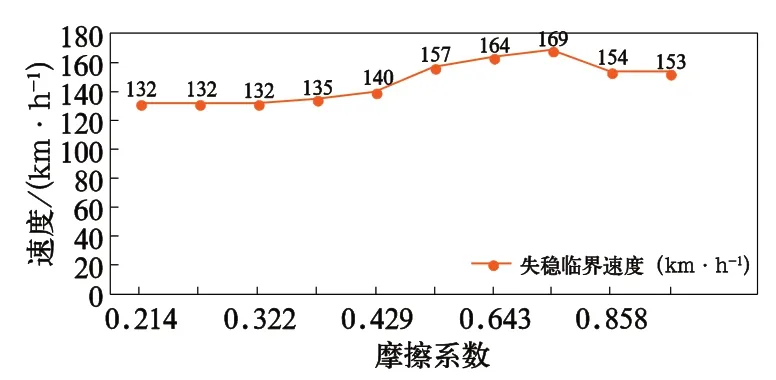
图3 摩擦系数与蛇行运动失稳临界速度的关系

通过以上仿真结果，将变摩擦减振器主摩擦面上安装的普通磨耗板改进为高分子材料磨耗板，相应的摩擦系数为0.5，此时蛇行运动失稳临界速度为157 km/h，但相比132 km/h 的速度值，安全冗余度小于20%，还不能满足车辆稳定性的动力学性能要求。

（1）为了提高安全冗余度，除了采用相对摩擦系数较高的高分子磨耗板外，在车体与转向架之间增加抗蛇行减振器，同时调整旁承的预压缩值，得出旁承预压缩量、抗蛇行减振器阻尼与蛇行运动失稳临界速度的关系如表4 所示。

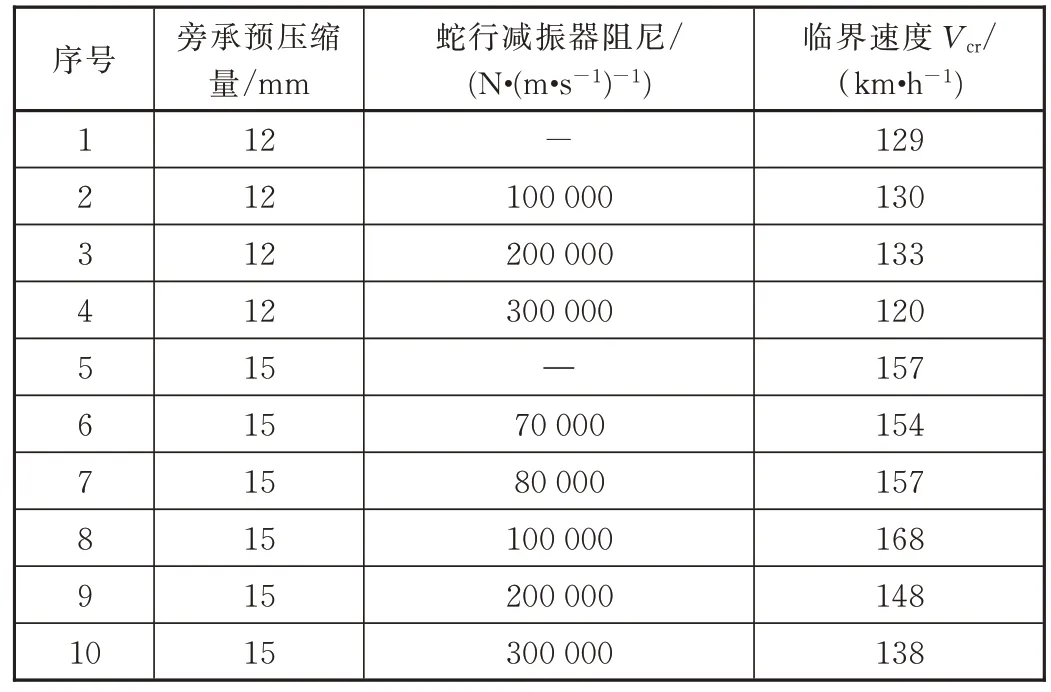
表4 抗蛇行减振器阻尼值、旁承压缩量与蛇行运动失稳临界速度的关系

从表4 的可看出，当旁承预压缩量为12 mm，抗蛇行减振器阻尼值为 200 000 N·(m·s−1)−1时，蛇行失稳临界速度值最大为133 km/h；当旁承预压缩量为15 mm，抗蛇行减振器阻尼值为 100 000 N·(m·s−1)−1时，蛇行失稳临界速度值最大为168 km/h。故旁承压缩量优选值为15 mm、抗蛇行减振器阻尼优选值为100 000 N·(m·s−1)−1，以下对上述参数优化后的模型进行动力学性能预测。

3.2 平稳性分析

平稳性仿真速度在50～132 km/h 范围内，每个工况速度在前一工况速度上增加10 km。

该型轨道工程车的横向和垂向振动加速度Ay、Az及横向、垂向平稳性指标Wy、Wz如表5 所示。计算结果表明:

（1）在132 km/h 速度范围内，车横向加速度最大值小于4.91 m/s2，垂向加速度最大值小于6.87 m/s2，满足标准规定的限度。

（2）在120 km/h 速度范围内，垂向平稳性指标小于3.0，达到“优秀”等级；在 130～132 km/h 速度范围内，平稳性指标达到“良好”等级。

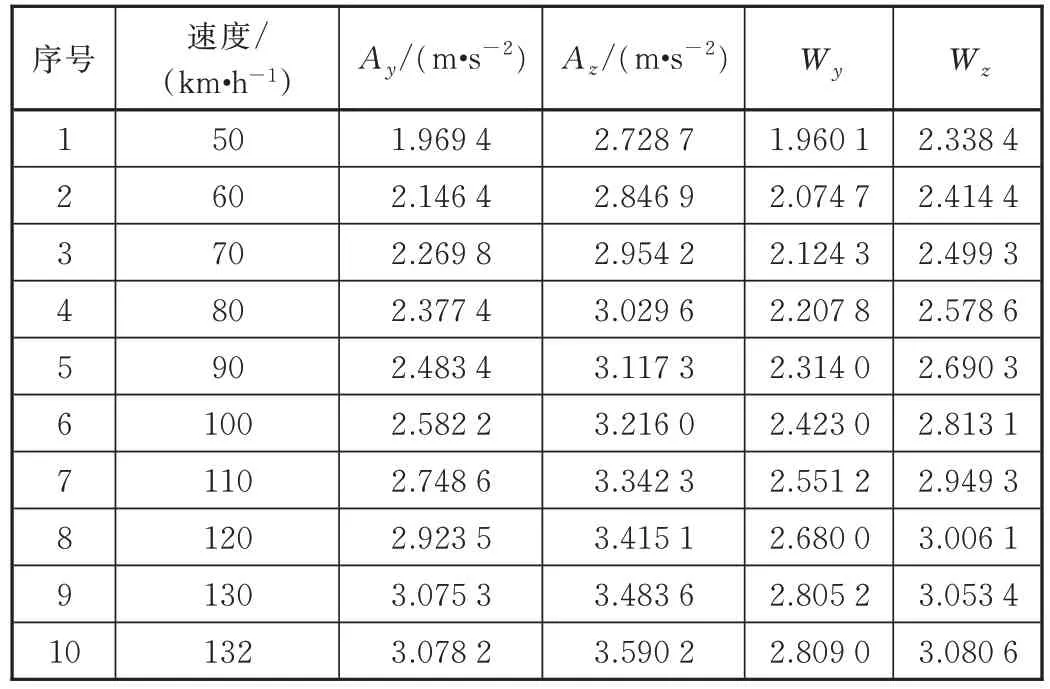
表5 振动加速度及平稳性指标

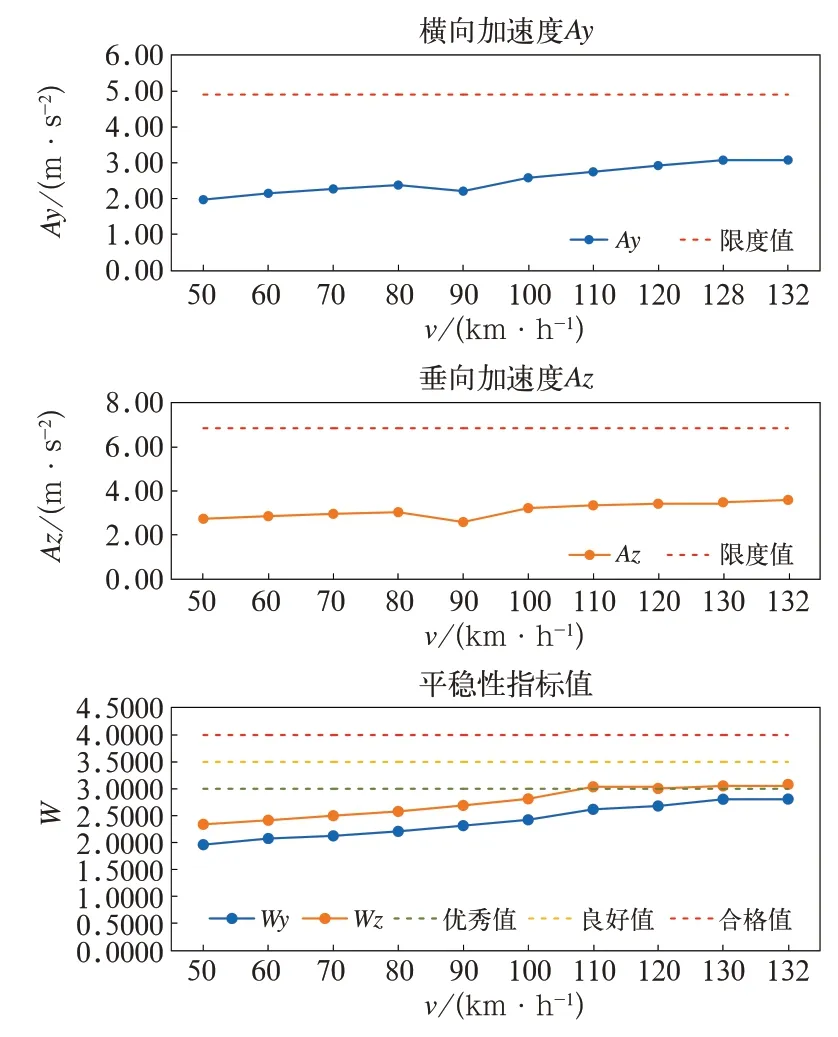
图4 最大振动加速度和平稳性指标值

3.3 安全性分析

本模型采用的轨道不平顺为美国5 级谱[1]，曲线半径取R=300 m、400 m、600 m，12 号单开道岔。曲线允许速度、欠超高量根据相关标准计算得到。动力学性能评价指标包括:轮轨横向力Q、轮轴横向力H、脱轨系数Q/P、轮重减载率ΔP/P、倾覆系数D。计算工况如下:

（1）曲线半径R=300 m，外轨超高h=100 mm、150 mm，最大欠超高90 mm，缓和曲线长度70 m，圆曲线长度60 m，最高运行速度69.5 km/h、78.1 km/h。

（2）曲线半径R=400 m，外轨超高h=100 mm、150 mm，最大欠超高90 mm，缓和曲线长度70 m，圆曲线长度60 m，最高运行速度80.3 km/h、90.2 km/h。

（3）曲线半径R=600 m，外轨超高h=80 mm、150 mm，最大欠超高90 mm，缓和曲线长度70 m，圆曲线长度60 m，最高运行速度93.0 km/h、110.5 km/h。

（4）以45 km/h 速度通过由12 号道岔组成的渡线。

该型轨道工程车通过曲线和道岔的计算结果如表6 所示。计算结果表明:轮轴横向力H、脱轨系数Q/P、轮重减载率ΔP/P、倾覆系数D均没有超过标准规定的限度。

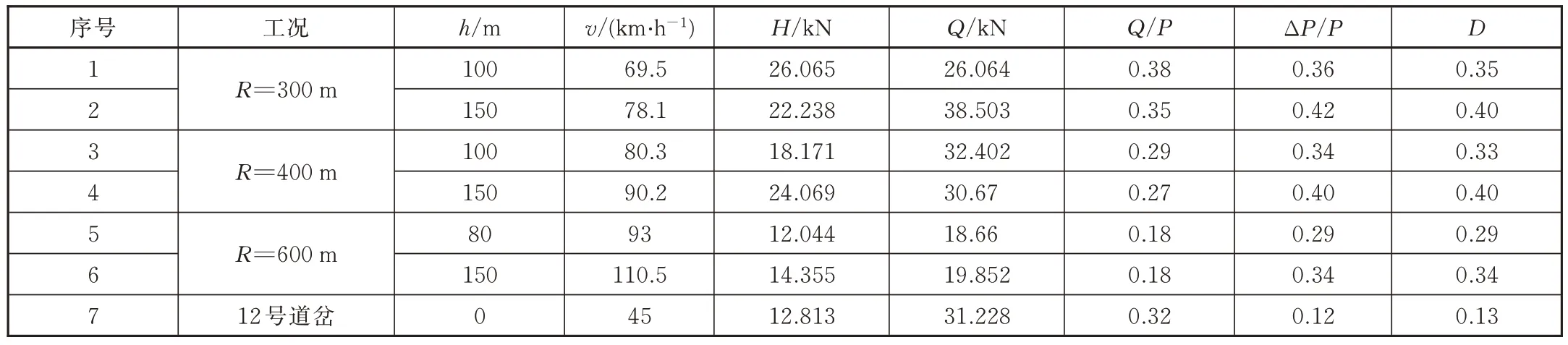
表6 曲线通过动力学性能指标

4 结 论

（1）根据用SIMPACK 仿真得出的变摩擦减振器摩擦系数、旁承压缩量、抗蛇行减振器阻尼值的变化对该型轨道工程车临界速度的影响，优选出摩擦系数值为0.5、旁承压缩量为15 mm、抗蛇行减振器阻尼值为100 000 N·(m·s−1)−1，此时该型工程车蛇行失稳临界速度为168 km/h，其平稳性指标和安全性指标均满足相关标准规范的规定。

（2）依据仿真结果，通过优化纵向定位、改进摩擦减振器的材料和增加抗蛇行减振器来提高临界蛇行速度和改善垂向振动后，动力学性能试验表明:该轨道工程车蛇行失稳临界速度不低于132 km/h；当试验速度为132 km/h 时，横向平稳性指标为2.98，垂向平稳性指标为3.16，和仿真结果接近，平稳性满足相关标准规范的规定；安全性满足相关标准规范的规定。通过应用SIMPACK 对轨道车辆系统进行动力学仿真分析，对车辆动力学性能参数选择具有实际的指导意义。