优化开关频率的六相永磁同步电机改进模型预测电流控制

郭宝双, 王爱元, 张言纯，李 恒

(上海电机学院,上海 201306)

0 引 言

永磁同步电机(PMSM)在工业制造业应用广泛。多相电机在同功率下有尺寸小、重量低的优势，其中六相电机因良好容错性开始用于电动汽车及风力发电领域[1]。

六相永磁同步电机开关电压矢量共有64个。最初矢量控制中忽略谐波子空间电流的影响，控制效果较差。文献[2]采用四矢量SVPWM算法进行电机控制，一定程度上降低了谐波电流，但生成的PWM波形不对称，实现困难。杂乱的PWM波形不利于减小谐波，会增大开关频率，进而引发器件发热，加剧变换器损耗。

模型预测电流控制(MPCC)为模型预测控制(MPC)中的一种，通过系统电流特性，利用计算机高速运算判断作用矢量[3]。六相PMSM中的MPC策略一般是将电压矢量中幅值最大的进行评估选取，以充分利用母线电压，提升了系统的动态性能[4-5]。六相电机的矢量空间可分为基波子空间与谐波子空间，谐波子空间对谐波电流影响巨大。文献[6]针对六相异步电机提出一种虚拟合成矢量的MPC策略，对电压矢量组合以消除谐波子空间电流分量，改善了电流脉动。不过矢量的合成并未考虑开关信号的形成，造成了多变的开关频率。文献[7]提出简化的模型预测转矩控制，改进了两步开关查找表以减少计算时间和电流谐波，然而仍未解决开关频率多变的问题。

本文针对六相PMSM系统控制中的多变的开关频率及电流谐波问题，提出一种优化开关频率的多矢量MPCC策略。首先，对基本电压矢量组合使在谐波子空间合成为零，生成虚拟电压矢量抑制谐波。其次，为优化开关频率，引入零矢量，并对虚拟合成矢量寻求易于PWM调制的等效替代矢量。最后，使用电流无差拍原理进行占空比调制，判断期望矢量扇区评估备选矢量，减少运算时间。仿真结果证实了该策略可有效改善开关频率，抑制谐波电流。

1 六相PMSM数学模型

选取的六相PMSM由空间相差30°的两套星形三相绕组(ABC及UVW)组成。运用矢量空间解耦(VSD)方法对变量进行坐标变换。VSD变换矩阵如下：

(1)

经上述变换可将变量分为两个正交子空间，即α-β基波子空间与x-y谐波子空间，前者参与能量变换，后者与谐波生成密切相关。对基波子空间变量进行同步变换：

(2)

由上述VSD变换，得d-q旋转坐标系及x-y子空间下的电压电流方程如下：

(3)

(4)

式中,ud，uq分别为定子d、q轴电压;id，iq分别为定子d、q轴电流;Ld，Lq分别为定子d、q轴电感;ωe为转子电角速度;R为定子电阻;ψf为永磁体磁链;ux，uy分别为x-y子空间电压分量;ix，iy分别为x-y子空间定子电流;Lz为漏自感。

2 改进模型预测电流控制

2.1 虚拟电压矢量合成

图1为六相PMSM中64个开关电压矢量在两个正交子空间依据八进制编号后的分布图。对矢量依据幅值分组，发现各矢量在两个子空间的作用效果不同。图中有C1、C2、C3、C4共四组有效矢量，C1与C4在谐波子空间中幅值大小互换，且均与C3相位相反，为尽量减小谐波，谐波子空间电压作用效果应接近零。

图1 空间电压矢量

本文可选择C1和C3组合或者将C3和C4组合，为充分利用直流母线电压，选择C3和C4合成虚拟电压矢量。举例说明即图中66、24、42矢量，24矢量在谐波子空间反相，故最终选择66、24矢量进行矢量合成。设母线电压为Vdc，基波子空间中C4、C3、C2、C1电压幅值分别为0.644Vdc、0.471Vdc、0.333Vdc、0.173Vdc，可得以下约束：

(5)

式中Tm、Tn分别为C4、C3的作用时间，T1为虚拟合成矢量的作用时间。求解得：

(6)

虚拟电压矢量等效如下式：

Vi=Tm·V最外层+Tn·V次外层

(7)

经计算，合成矢量幅值为0.597Vdc，共合成12个虚拟电压矢量，分别为V1(65,44)、V2(46,64)、V3(24,66)、V4(62,26)、V5(36,22)、V6(23,32)、V7(12,33)、V8(31,13)、V9(53,11)、V10(15,51)、V11(41,55)、V12(54,45)。

2.2 开关频率优化

上述虚拟合成矢量均消除了谐波子空间电压分量，经计算评估后将选取的合成矢量PWM调制后生成开关信号送入开关管。下面对开关信号波形进行分析，图2为不同的矢量生成的开关信号。

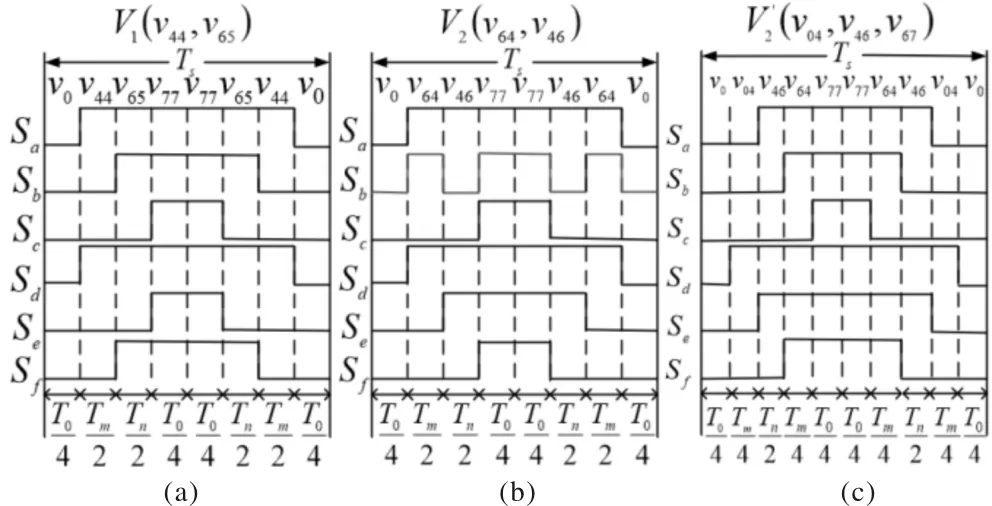
图2 不同矢量开关信号图

图2(a)为V1开关信号，与V3、V7、V9、V11信号相同在每个采样周期开关两次。图2(b)为V2开关信号，其中Sb信号单周期开关六次，V4、V6、V8、V10、V12也类似，增加了信号生成的难度，对谐波抑制产生消极作用。

图3 虚拟电压矢量

2.3 占空比计算及矢量选择

使用一阶欧拉公式对式(3)离散化，得电流预测方程为

(8)

式中，id(k)、iq(k)、id(k+1)和iq(k+1)分别代表d、q轴在k及k+1时刻的采样和预测电流；ud(k)和uq(k)分别代表d、q轴在k时刻的采样电压；Ed(k)和Eq(k)分别代表k时刻d、q轴反电动势值；Ts为采样周期。

系统运行中通常会有单步计算延迟，影响控制性能，使用两步预测补偿该误差，k+2时刻预测电流如下：

(9)

使用电流无差拍原理计算占空比[8-9]，本文选用id=0控制方式，对q轴电流求期望值如下：

(10)

式中，t1为预选电压矢量的作用时间；s1为预选电压矢量作用时iq的斜率；s0为零电压矢量作用时iq的斜率。计算公式如下：

(11)

(12)

式中，uq_opt为预选电压矢量对应的定子交轴电压。联立式(10)～式(12)，求得虚拟矢量作用占空比及作用时间T1为

(13)

T1=D*Ts

(14)

对虚拟矢量前后15电角度设定为一个扇区，对期望矢量变换得基波电压分量，作如下计算求角度判断扇区[10]：

(15)

判断扇区后，仅使用扇区内虚拟矢量及零矢量对应定子电流代入价值函数，可减少计算时间，价值函数如下：

(16)

由上式选择最小值对应矢量作用于控制系统。将虚拟电压矢量与零矢量相结合的占空比调制使得作用矢量幅值可调，最终生成优化过的开关信号。

3 仿真分析

在Matlab/Simulink中搭建仿真模型，对比验证六相PMSM优化开关频率后的MPC控制效果。本文选取了传统MPC控制策略与提出的改进MPC控制策略进行了对比研究。

仿真所涉及的参数如表1所示，采样频率均为10 kHz。图4～图7为两种控制方式转速及电流响应图。图8为相电流FFT分析图。

图8 两种控制方式的FFT分析图

表1 电机参数

图4～图7为两种控制方式的转速及电流响应图。为清晰观察两种控制方式的负载扰动抗性，在0.15 s时刻突加负载60 Nm。

图4 两种方式转速响应比较图

图5 两种控制方式的相电流脉动图

图6 两种控制方式的dq轴定子电流脉动图

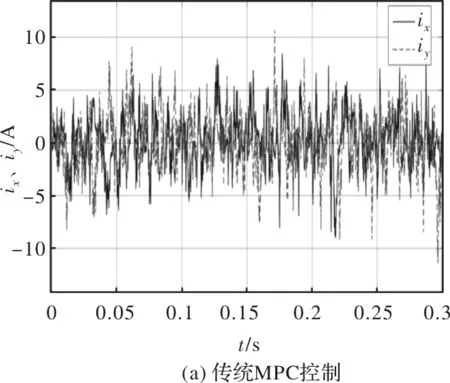
图7 两种控制方式的谐波子空间定子电流

上面将两种控制方式下系统转速及电流参数波形图列出，下面对波形具体分析。观察图4转速响应，在经过大约0.01 s后相应曲线趋于稳定，可看出两种控制方式均有较为迅速的动态响应性能。在加入负载转矩后，放大转速曲线可看出，传统MPC策略在0.02 s后达到稳定状态，改进MPC策略在0.01 s后稳定，两种控制方式响应速度相当。图5为相电流波形图，观察曲线可得，改进MPC策略有更小的电流脉动，尤其加入负载转矩后波形更接近于正弦波。图6为两种方式定子直、交轴电流图，由于反应的更多为系统动态响应速度，观察得二者波形相近，无明显差别。图7为两种控制方式谐波子空间定子电流波形图，传统MPC策略谐波幅值基本在5 A左右，改进MPC策略针对谐波子空间效应做出优化，观察得其谐波幅值在2 A上下波动，系统谐波大大降低了。

为具体说明两种控制策略谐波抑制效果，使用Matlab/Simulink中的傅里叶谐波分析工具箱FFT对相电流进行定量分析，结果如图8所示。对传统MPC控制方式分析得谐波畸变率(THD)为29.49%，优化开关频率的改进MPC控制方式相电流谐波畸变率为12.37%。

分析上述仿真结果，在动态性能上，两种MPC控制方式具有相近的控制效果，响应迅速。在稳态性能方面，本文提出的MPC控制比传统MPC控制方式具有更小的电流波动，极大地减小了谐波电流。

4 结 语

本文针对六相PMSM提出了一种新型的MPCC控制方式。首先选取矢量组合使得该虚拟矢量在谐波子空间作用效果为零，抑制谐波生成。虚拟矢量PWM调制后开关信号多变，选取替代矢量等效原先矢量，生成12个替代虚拟矢量，便于PWM调制，降低开关频率。为了进一步降低系统误差，结合零电压矢量，使用无差拍电流原理，完成矢量占空比调制。最后计算期望电压矢量角，选择扇区矢量代入价值函数，减小了系统一定的运算负担。