引射器活门调节机构的流固热耦合特性

2021-01-15孙永航葛长闯许春阳

东北大学学报（自然科学版） 2021年1期

罗忠，孙永航，葛长闯，许春阳

(1.东北大学机械工程与自动化学院，辽宁沈阳 110819； 2.东北大学航空动力装备振动及控制教育部重点实验室，辽宁沈阳 110819； 3.中国航发沈阳发动机研究所，辽宁沈阳 110015)

在现代高性能航空发动机和燃气轮机的发展过程中，逐渐使用了各类的运动调节机构.对航空发动机与燃气轮机的性能要求不断提高的同时，运动调节机构的精度和可靠性要求也不断提高，其动力学性能决定着整机关键结构的性能、稳定性和可靠性.以本文研究的某型船用燃气轮机排气引射器活门调节机构为例，其在工作过程中承受着热载荷、气动载荷等外部载荷的共同作用，极易发生故障，关乎着整机的安全运行，因此对活门机构的强度与寿命研究是非常有必要的.

对于航空发动机与燃气轮机的几类典型运动机构而言，现存的气动特性的研究较为广泛，静叶调节机构[1-2]、喷管[3-4]、反推[5-6]、变几何涡轮[7]等机构的气动基础研究已较为扎实.对于本文的弯管引射器，Maqsood等[8-10]对其气动特性也已有了较为深入的研究.而对航空发动机与燃气轮机来说，单一物理场下的研究是远远不够的，已有学者对航空发动机的多场耦合问题展开研究[11-14]，但对几类典型运动机构的多场耦合研究还比较少.Butterfield等[15]结合二维流场分析与三维有限元分析，实现了叶栅式反推力装置的流固耦合，并作为减重设计的依据.王彦等[16]针对轴对称矢量喷管机构，研究了喷管从低温低流速到高温高流速过程中机构的应力应变及温度变化.

对于活门机构来说，其所受的气动载荷来自于高温燃气与被引射气流的共同作用，所受的热载荷是由高温燃气导致，而离心载荷则由于活门阀片的快速打开导致的.针对典型运动调节机构中气动、温度、结构多场耦合分析研究不足的问题，本文建立了引射器整体三维流场以及活门阀片的结构模型，采用计算流体动力学(computational fluid dynamics，CFD)方法，分别对流场进行了稳态仿真与瞬态仿真，并讨论了其适用性，进行了考虑热载荷、气动载荷和离心载荷耦合作用的结构强度分析.

1 计算模型与控制方程

1.1 计算模型

本文以某型船用燃气轮机排气引射器活门调节机构为研究对象，原理图如图1所示.图1a为典型引射器示意图.典型引射器由3个轴对称的套筒组成，从外到内依次是外罩、排气筒和内锥体.其中内锥体和排气筒之间的箭头表示高温燃气，在排气筒出口处与空气掺混，形成较低温度的气体.图1b为本文采用的带活门引射器.活门周向均布8个，位于排气筒入口处，完全打开时与轴线成45°，在排气筒内部形成8个波瓣，阻挡部分气流，同时将空气与高温燃气提前掺混，使排气筒内部的气流温度降低.

在计算中，选取整个引射器的流场，以及活门机构阀片的结构模型为计算区域，模型如图2所示.相关尺寸如下：引射器外入口段外径为1 000 mm，排气筒外径为780 mm，内锥体外径为450 mm.对于活门机构阀片，其厚度为2 mm，宽度为120 mm，长度为240 mm.

常用两种方法对该运动调节机构进行流场研究:一种是工程实际中常用的阀片固定开度的稳态仿真；另一种是阀片开启的瞬态仿真[17].稳态仿真的特点是将阀片固定到某个开启高度，使密封面内外流域连通，进行流场分析；瞬态仿真则不同，利用动网格方法来实现阀片的动态开启.相对于稳态仿真，瞬态仿真充分考虑了开启过程的动态特性.本文同时基于这两种方法进行了活门调节机构的流场仿真并进行对比，选取合适的方式进行多场耦合计算，为结构的设计优化提供参考.

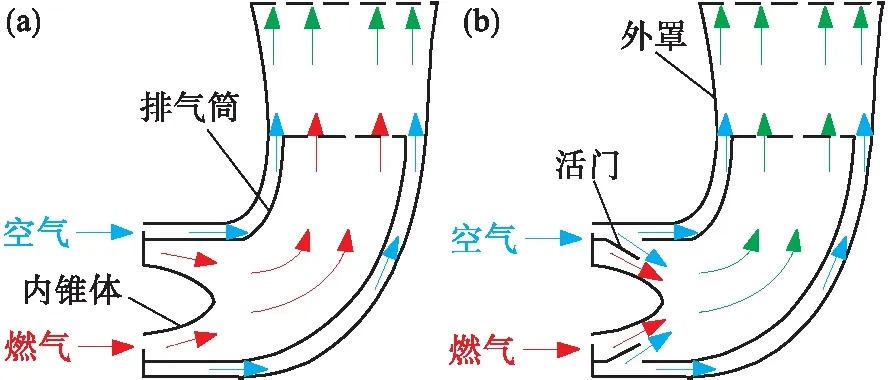
图1 引射器原理图

图2 计算模型

1.2 控制方程

1) 结构的动力学方程.活门机构阀片的结构动力学方程可以描述为

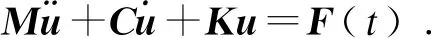
(1)

2) 流体的控制方程.对于流体域，在CFD的计算过程中需同时满足质量守恒、动量守恒和能量守恒.

对于质量守恒方程，可表示为

(2)

式中：ux,uy,uz分别为x,y,z方向上的速度分量；t为时间；ρ为密度.

动量守恒方程，又称纳维-斯托克斯方程(Navier-Stokes equation)，表示为

(3)

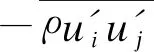
对于能量守恒方程，可写为

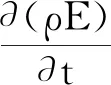
(4)

式中：E为流体的总能量；为散度；Hj为组分j的热焓；ke为传热系数；τe为应力张量；Jj为组分j的扩散通量；S为体积热源项.

3) 热传导方程.高温燃气通过流道使活门机构温度升高，属于典型的热传导.对于各向同性材料，在无内热源的条件下，热传导微分方程为

(5)

式中：c为比热容；λ为热导率；T为温度.活门机构各部分受热不均且受边界条件的约束，会产生热应力，对结构强度产生影响.

2 多物理场耦合分析流程

2.1 分析步骤

由于活门阀片的变形对于流场的影响较小，所以本文采用顺序单向耦合的方法，即先对引射器流场进行CFD分析，然后将上述计算结果作为热分析及强度分析的边界条件进行求解.具体分析步骤如图3所示，主要步骤为

1) 根据实际结构建立流场与结构的模型；

2) 利用CFD软件Fluent进行流场的仿真，获取流体域的压力与温度数据；

3) 将表面温度插值到结构模型中，对其进行热分析，并将求解的温度作为热边界条件；

4) 将表面压力插值到结构模型中，完成压力载荷与离心载荷的施加；

5) 完成调节机构的多场耦合动力学特性分析.

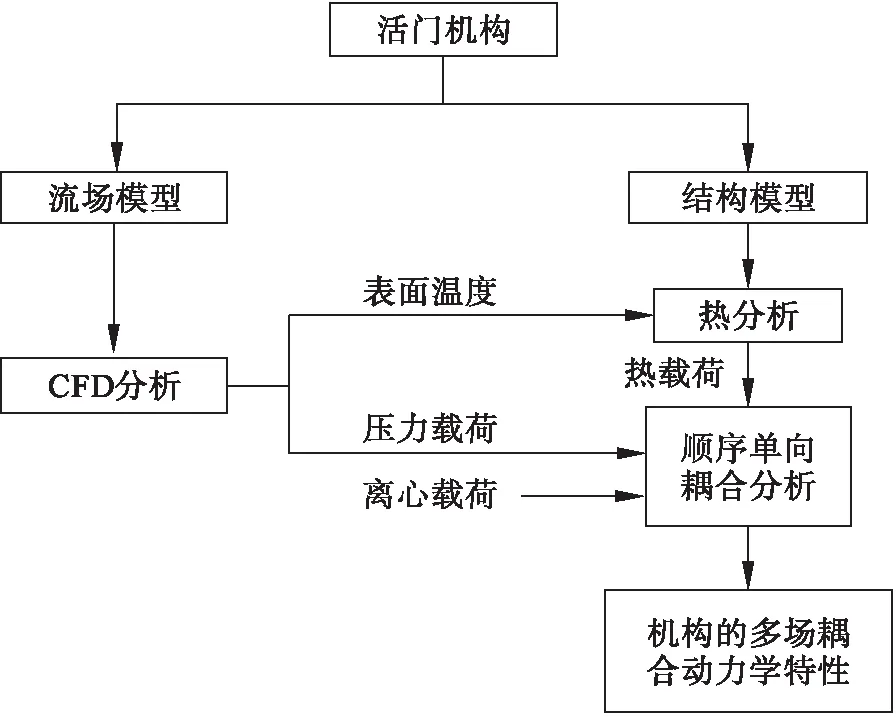
图3 顺序单向耦合分析步骤

2.2 载荷传递

在CFD的分析中，可以得到阀片表面节点上的压力与温度，前者为矢量，方向为垂直表面向内，后者为标量.要想使流场计算的压力与温度施加在结构模型上，需要解决两者网格不匹配的问题，即对其进行插值传递.ANSYS中所使用的插值方法为零阶插值法，又称最邻近插值法，主要原理是让输出值等于邻域内离它距离最近的值.因此，要想保证插值结果的准确性，应尽量保证流场与结构网格一致.本文所划分的两者网格之间有着90%以上的匹配度，保证了数值传递的准确性.

3 流场计算与分析

3.1 计算有效性验证

首先对稳态仿真方法进行计算有效性验证.采用Maqsood等[8]的试验台模型，混合管与水平位置夹角45°.采用四面体非结构化网格，网格总数为30 000，网格划分情况如图4所示.高速流入口采用质量入口，质量流量为1.6 kg/s，引射大气入口采用压力入口，稳态仿真计算至收敛后，提取出口表面速度云图，与文献[8]中结果对比如图5所示.

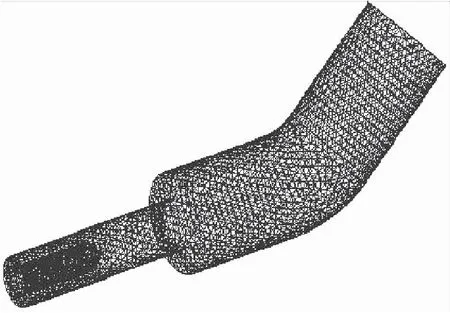
图4 Maqsood试验台网格划分

引射比作为表征引射器性能的特征参数，表示为二次流的质量流量与主流的质量流量之比，其计算式为

(5)

其中：qm1为主流的质量流量；qm2为二次流的质量流量.引射比的仿真结果与文献对比如表1所示.

综合流速对比与引射比对比，本文的结果与文献中的仿真结果较为接近，验证了引射器稳态仿真方法的可行性.

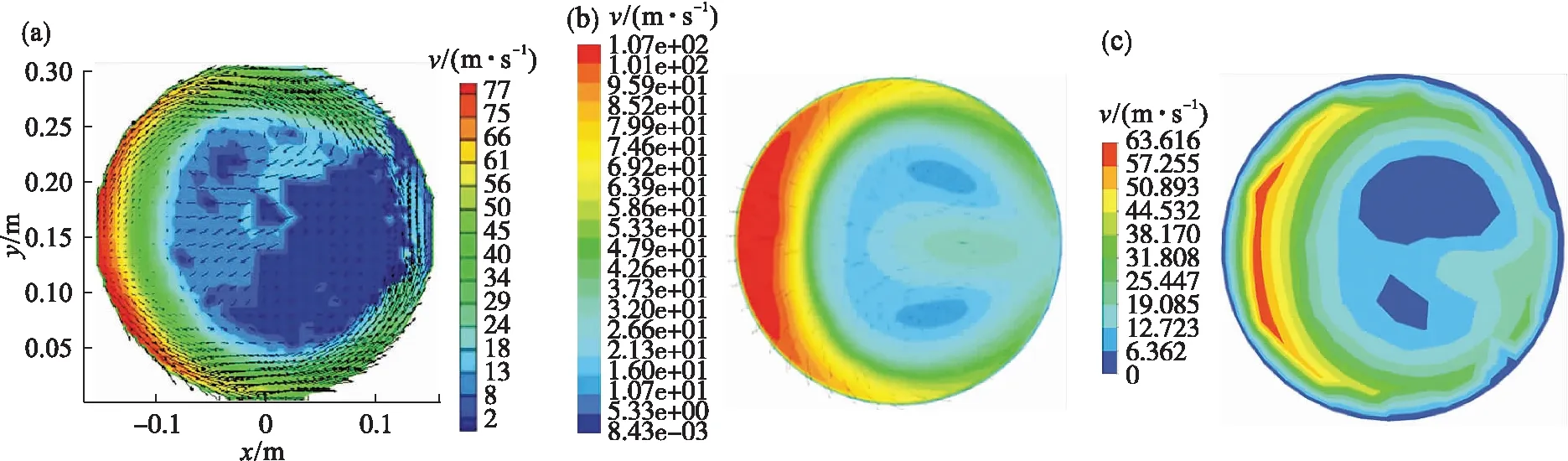
图5 流速对比结果

表1 引射比对比

3.2 稳态数值求解

在计算有效性验证的基础上，以固定阀片开度的方式进行稳态数值求解.采用CFD方法对流体域进行仿真，网格总数为244 958，节点总数为47 996.选择标准k-ε模型及隐式求解方法，参数设置如表2所示.

表2 参数设置

在计算完成后，提取阀片表面的压力载荷，阀片开度45°时上、下表面的压力云图如图6所示.对于阀片的下表面而言，其根部中间区域的压力最大，这是由于高温燃气入口的冲击所导致的，位于圆周均匀分布的8只阀片呈现了同样的趋势.

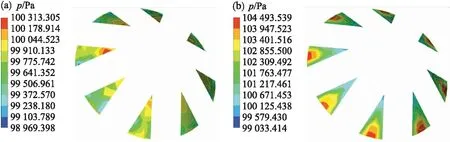
图6 阀片表面压力云图

3.3 瞬态数值求解

阀片的运动由动网格算法控制[18]，根据动网格仿真时对网格的要求，在网格划分时，在入口段，即阀片运动区域，为确保网格正常地生成与销毁，划分时使用了四面体网格，其余部分采用六面体扫掠网格.网格总数为1 203 103，节点总数为239 723.动网格区采用Lagrange算法，网格可拉压变形，静止网格区采用Euler算法，两者的交界面采用interface边界，通过数值插值实现了各流体区域之间计算结果的传递.结合“弹性光顺”与“网格重构”算法，使得被定义的wall面按照既定的旋转轴和旋转速度运动.选择标准k-ε模型及隐式求解方法，阀片运动0.4 s，转动45°，时间步长取0.000 2 s，计算总时间0.4 s，其余边界条件与稳态相同.

阀片开度每5°提取一次压力云图，阀片表面压力云图如图7所示.由图7可以清楚地看出开启过程中其表面时变压力载荷的变化情况.随着开启角度的逐渐增大，阀片下表面与高温燃气的接触面积增大，因此其所受的压力也逐渐增大.与固定开度的稳态仿真不同，瞬态仿真反映了表面压力的连续变化，充分体现了瞬态特性的影响.

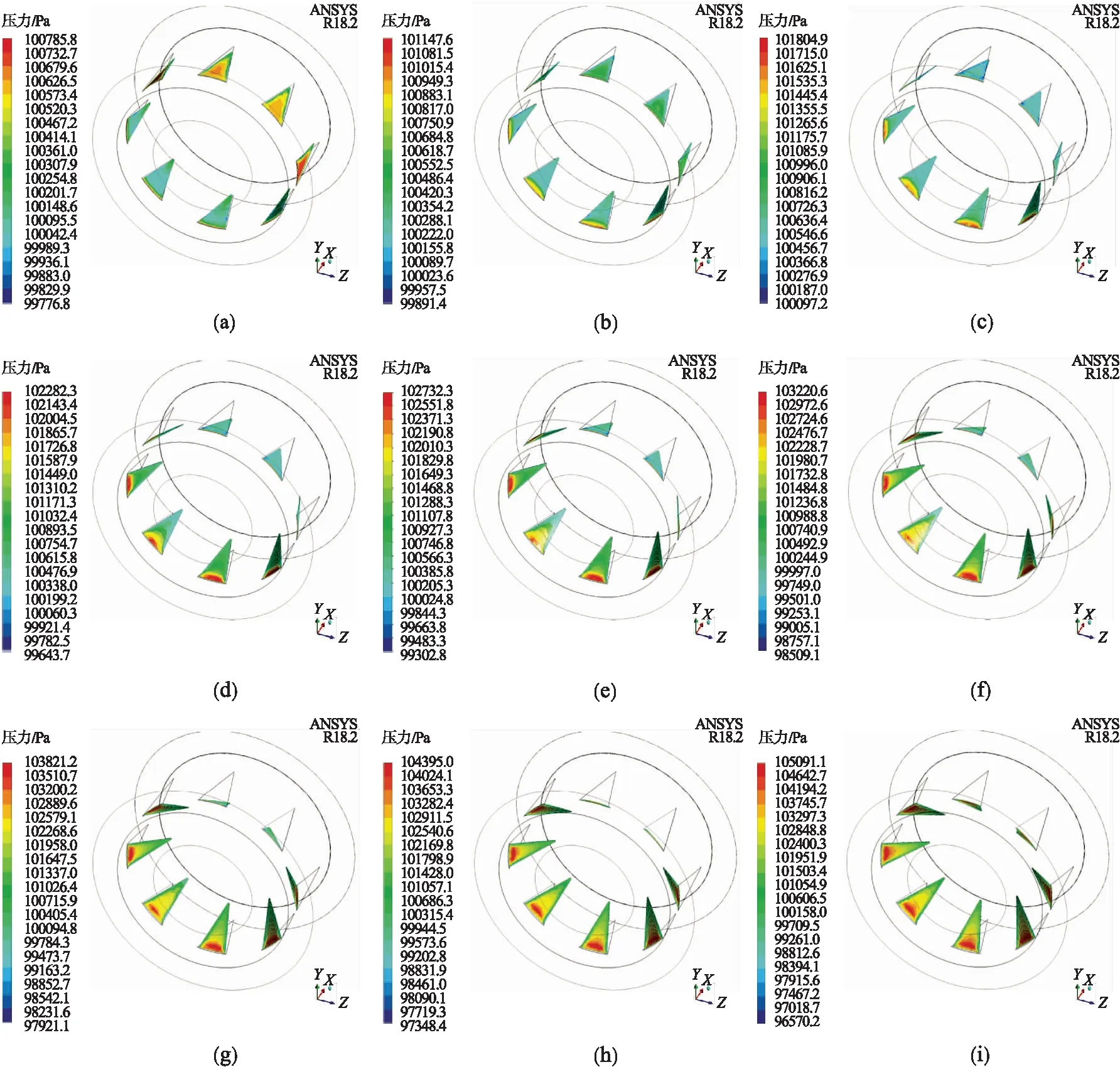
图7 三维瞬态仿真引射器阀片表面压力云图

图8为引射器活门调节机构阀片瞬态与稳态压差对比图.纵坐标表示阀片下表面与上表面压力的差值.在5°至45°的运动区间里，相较于稳态仿真而言，瞬态仿真的压差明显更大.由此可以得出结论，在燃气轮机运行状态改变的过渡态，阀片的时变载荷不能仅仅采用稳态求解的方式，其平均值要明显小于瞬态求解的值，这可能导致设计时强度估计不足，为保证工作期间的安全性，需对其进行瞬态计算，并充分考虑冲击、振动等因素的影响.因此，在下文的多场耦合计算中，将采用瞬态求解的压力与温度值.

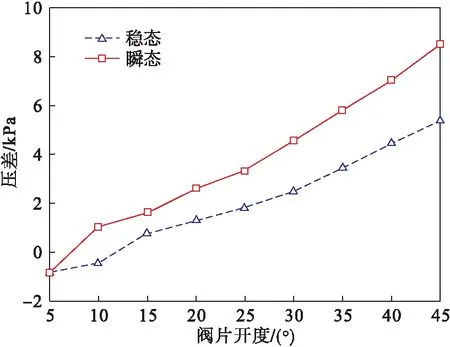
图8 活门机构阀片瞬态与稳态压差对比

4 耦合计算与分析

4.1 有限元参数设置

基于瞬态仿真的结果，对某型燃气轮机排气引射器活门机构阀片进行流固热耦合研究.阀片在实际工作中主要承受离心载荷、热载荷、气动载荷的影响，本节在耦合计算中，考虑对上述三种载荷进行施加.

采用实体单元对活门机构阀片进行建模，结构网格总数为2 498，节点总数为15 627.阀片的材料为镍基变形高温合金GH4169，其密度为8 420 kg/m3，泊松比为0.3.求解时，将阀片尾部设为固支边界条件.各温度下材料的弹性模量如表3所示.

表3 各温度下材料的弹性模量

4.2 热分析

由于在CFD计算中获得的温度为结构的表面温度，因此需首先进行结构热分析获得阀片的整体温度.

计算所得的阀片运动至45°时的温度分布如图9所示.对于活门机构区域，其下方是高温燃气，上方是空气，活门打开后两者掺混.这种温度情况也正好体现在阀片上：其下表面承受着高温燃气，整体温度较高，在上表面高温燃气与空气掺混，导致其温度较低.将热分析所得温度作为结构分析的边界条件，进行多场耦合计算.

4.3 多场耦合分析

对活门机构阀片而言，其受到气动载荷、热载荷、离心载荷三种外载荷的共同作用.本小节在多场耦合计算求解的同时，也讨论了几种载荷单独作用的影响.

首先单独分析了离心载荷对活门运动机构阀片的影响.阀片在极端条件下的最大转速约为4 rad/s，所产生的最大结构变形为3×10-4mm，最大等效应力为0.01 MPa，因而离心载荷对阀片的强度影响很小，可以忽略不计.

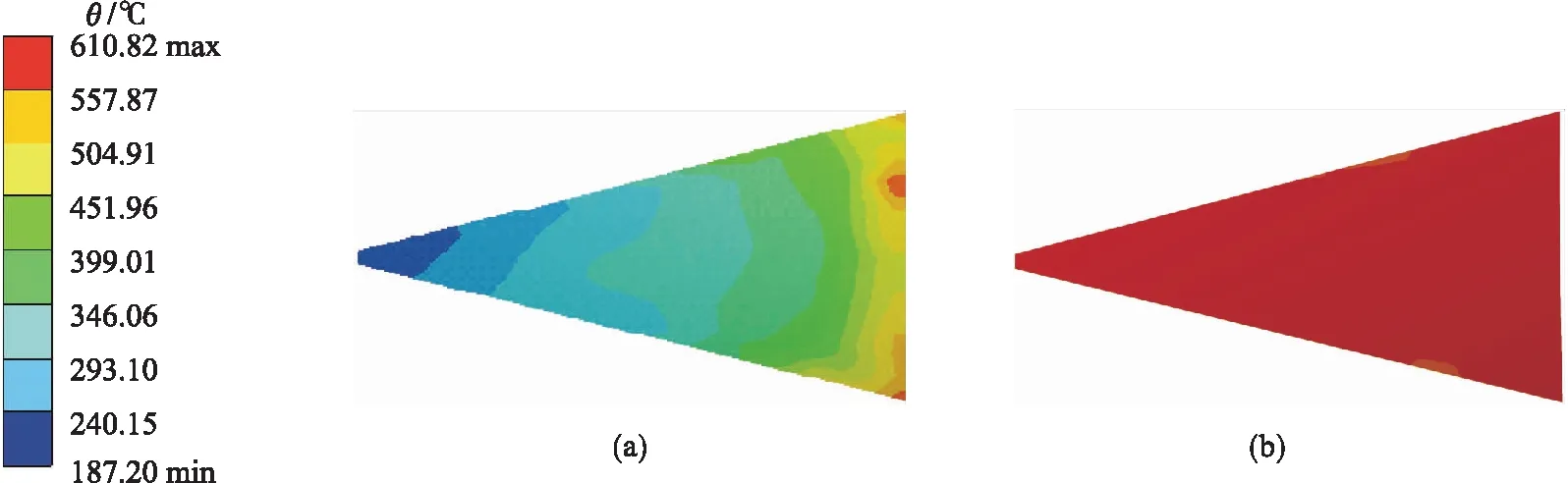
图9 阀片运动至45°时的温度分布

对阀片分别进行了多载荷作用、气动载荷作用和热载荷作用下的强度分析，得到了上述三种工况下的最大变形和最大Von Mises应力，如表4及表5所示.由表4可以发现，随着阀片开度的增加，气动变形量一直在增大；热载荷作为变形产生的主要原因，其值要远远大于气动变形量，呈现先增大后减小的趋势；而多载荷作用的变形量与占主导的热载荷的变形量十分接近.在活门开启的过程中，阀片上下表面的温差最大可达到400 ℃，这也是热变形较大的主要因素.

在表5中对比了几种工况下产生的最大等效应力.由前文计算的瞬态气动载荷可知，阀片表面的压差随开度增加逐渐增大，单独考虑气动载荷作用下的气动应力变化趋势正好与之相符.对于活门机构而言，对比离心、气动与热三种载荷，其所受的最大载荷为热载荷，而气动载荷的存在，降低了热载荷所产生的弯曲应力，使得多载荷作用下的等效应力相对热应力而言更小.

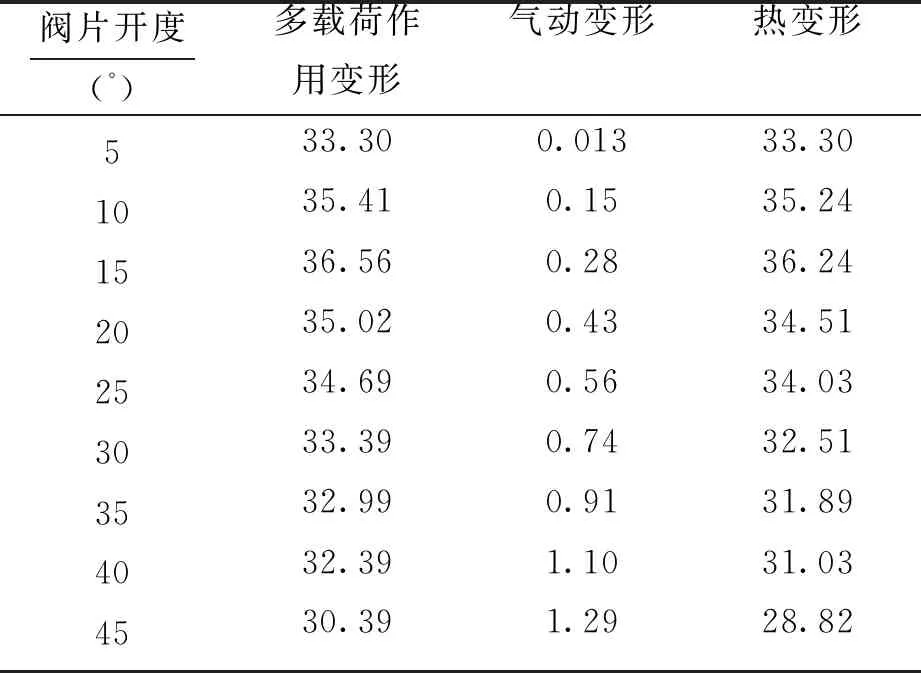
表4 不同载荷作用下阀片的最大变形

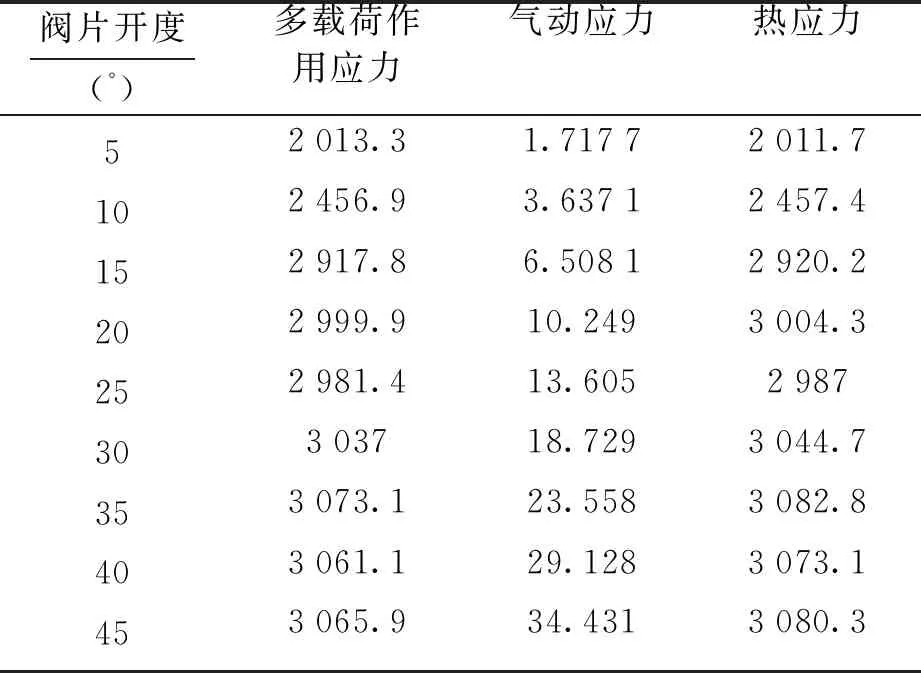
表5 不同载荷作用下阀片的最大等效应力

耦合计算后阀片运动至45°时的Von Mises等效应力及变形如图10所示.由图10a可以看出，阀片此时的最大变形量为30.391 mm，出现在其尖端.由于尾部的固支边界条件，且其形状为等腰三角形，使得阀片前半部向上翘起.图10b为应力分布图，最大等效应力为3 065.91 MPa，应力集中出现在阀片根部区域，应力呈现两侧较大、中间较小，且左右对称的分布.