基于遗传算法对供应链订购问题的研究

张波 梁哲 莫淇皓 马龙

摘  要：针对生产企业原材料的订购规划类问题，首先运用公式法评估企业生产的重要性，运用Excel软件得出50家最重要的供应商，其次运用遗传算法构建了最优订购方案模型，综合运用了MATLAB、Excel等软件进行问题的求解，得出了最少供应商的结果，最后结合实际给出合理化建议。文章在分析供应链的需求的基础上，运用遗传算法解决了生产企业原材料的订购问题。

关键词：供应链;遗传算法;公式法;评价模型;规划模型

中图分类号：TP18      文献标识码：A文章编号：2096-4706（2021）14-0170-04

Abstract： Aiming at the ordering planning of raw materials in production enterprises， this paper first uses the formula method to evaluate the importance of enterprise production， obtains 50 most important suppliers by using Excel software， then constructs the optimal ordering scheme model by using genetic algorithm， comprehensively uses MATLAB， Excel and other software to solve the problem， and obtains the result of the least suppliers. Finally， combine with practice， some reasonable suggestions are given. Based on the analysis of the demand of supply chain， this paper uses genetic algorithm to solve the ordering problem of raw materials in production enterprises.

Keywords： supply chain; genetic algorithm; formula method; evaluation model; planning model

0  引  言

供應链管理的概念是在八十年代中期提出的，当时管理者普遍单方面优化了供应链的管理，以一种独立的管理模式实现了企业的生产链和配送，提高了企业的经济效益和社会效益，但这种企业管理方式并没有达到预期的效果。从整个供应链的角度，即从总成本的角度，优化和改进公司管理，以促进管理朝着组织和诚信的方向发展。[1]是否赢利与成本及生产力息息相关，因此对一个决策做出合适的评价和优化对企业的经营状态起着至关重要的作用。

本文的特色是在分析供应链的需求上，运用遗传算法解决生产企业原材料的订购问题。

1  问题分析

问题一要求选择合适的评估指标体系，评估企业生产的重要性。首先回顾相关资料，分析哪些指标影响企业生产;其次是将所选指标与相关指标体系挂钩，筛选合理指标，建立可靠及时的评价指标体系;最后根据建立的指标体系得出50家最重要的供应商。

问题二要求我们参考问题一，建立供应商最少模型。对于此问题，首先，我们将本问归为规划类模型;其次，按照规划类模型的解题思路，我们决定从三个方向入手：决策变量、目标函数和约束条件;最后根据得出订购方案。

2  模型建立与求解

假设该企业在第一周时存储的原材料量为0;企业在满足生产条件的前提下可以接受的容错率为70%;企业每周需保持的生产库存为本周和下一周的生产库存;每年每周的损耗量的均值对应每周每个公司的损耗;供货商每周的供货量为当前周生产的;企业的订货量为该供应商每一年供货量的最大值。符号说明如表1所示。

2.1  问题一的建立

针对此问我们对“供应商”的供货特征进行了量化分析，并进行评价，模型的建立，评价供货商对企业生产的进行评定，并将进行排名。

根据原题，表格中有402家供应商240周的数据，分别为企业的“订货量”记为N订，供应商的“供货量”记为N供。建立的评价指标有：

（1）供货准确率：表示企业的订货量与供货商的供货量的误差比例，系1减去计算订货量与供货量的差的绝对值，除以订货量的方式进行比对，供货准确率越大则该供货商越值得信任，对于企业的生产就越有保证。

在供货量不为0时，供货准确率的计算公式为：

总的供货准确率取有效周的均值，公式为：

（2）供货完成率：表示企业的订货量大于等于供货商的供货量的情况占总体订单情况的比例，当企业收到的货大于等于订货量时记为“供货完成”。供货完成率越大表示企业可以更信任该供应商，企业自身不会因为原材料短缺而造成直接的经济损失，所以供货完成率是保证企业生产的必要条件。计算公式为：

（3）大额订单比例：对于供应商来说，大额订单所占比例越大，供货就越稳定，在增加产能的情况下大概率可以提供更多的原材料，所以大额订单的比例就对于企业来说变得尤为重要。计算公式为：

（4）容错性企业在运营过程中应该具有一定的抗风险能力，当供应商不能满足企业的需求时，只要在一定的范围内，企业是可以接受直接的经济损失的，所以我们暂定当准确率达到70%及以上时企业是可以接受的，所以，容错性就是供货准确率达到70%及以上占总订单的比例。容错性越大代表企业可以接受的风险水平越高，企业的生产也就有了保证。其计公式为：

我们以供应商的原材料的类别为分类依据，对A、B、C、三类原材料供应商进行了量化分析，分析结果如表2所示。

从表格中可以清晰地看到，原料C的各种综合指标都是三种材料中最优秀的，所以企业更需要原料C的供应商，相反原料B的供应商是最不出色的，所以在后续供应商多选择原料A与原料C的供应商。

对于个体供应商对于企业的可信任性评价，我们通过前面的评价指标进行评价模型的建立，约束条件有以下几点：

供货完成率越大，供货准确率越大;大额订单的比例越高，容错性越大，则供应商对于企业的可信任性就越高。

故我们建立的可信任性评价模型为：

δ=（βε+γ）*α

其中δ表示供应商对于企业的可信任性。

根据我们针对企业对供应商的建立的可信任性模型，得到了402家供应商中50家比较值得信任的供货商，如表3所示。

2.2  问题二的建立和求解

本问是典型的规划类问题，根据题目与第一小问的结果来推断出最终的预定方案和转运商选择方案，故，按规划类问题的求解思路，我们设立了决策变量，目标函数，约束条件，三个解题方向进行规划类分析，并总结出最优解。

在第二问中我们进行了合理的假设，因为我们需要找得到最少的供应商数量就是题中所说的在满足生产的基础上进行最少的供货商的选择。因为体重主要是重视供货阶段，并不是在转运上，所以我们假设转运过程中的损耗只有2%，所以企业的接收量为供货商供货量的98%。

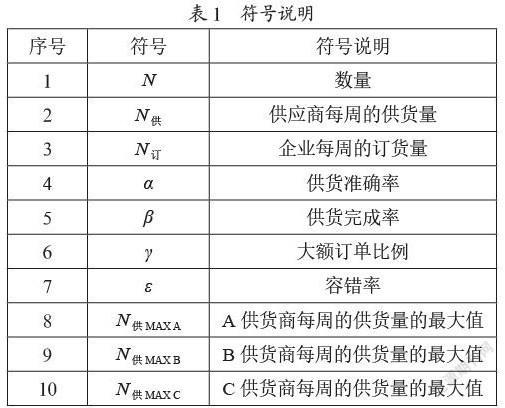
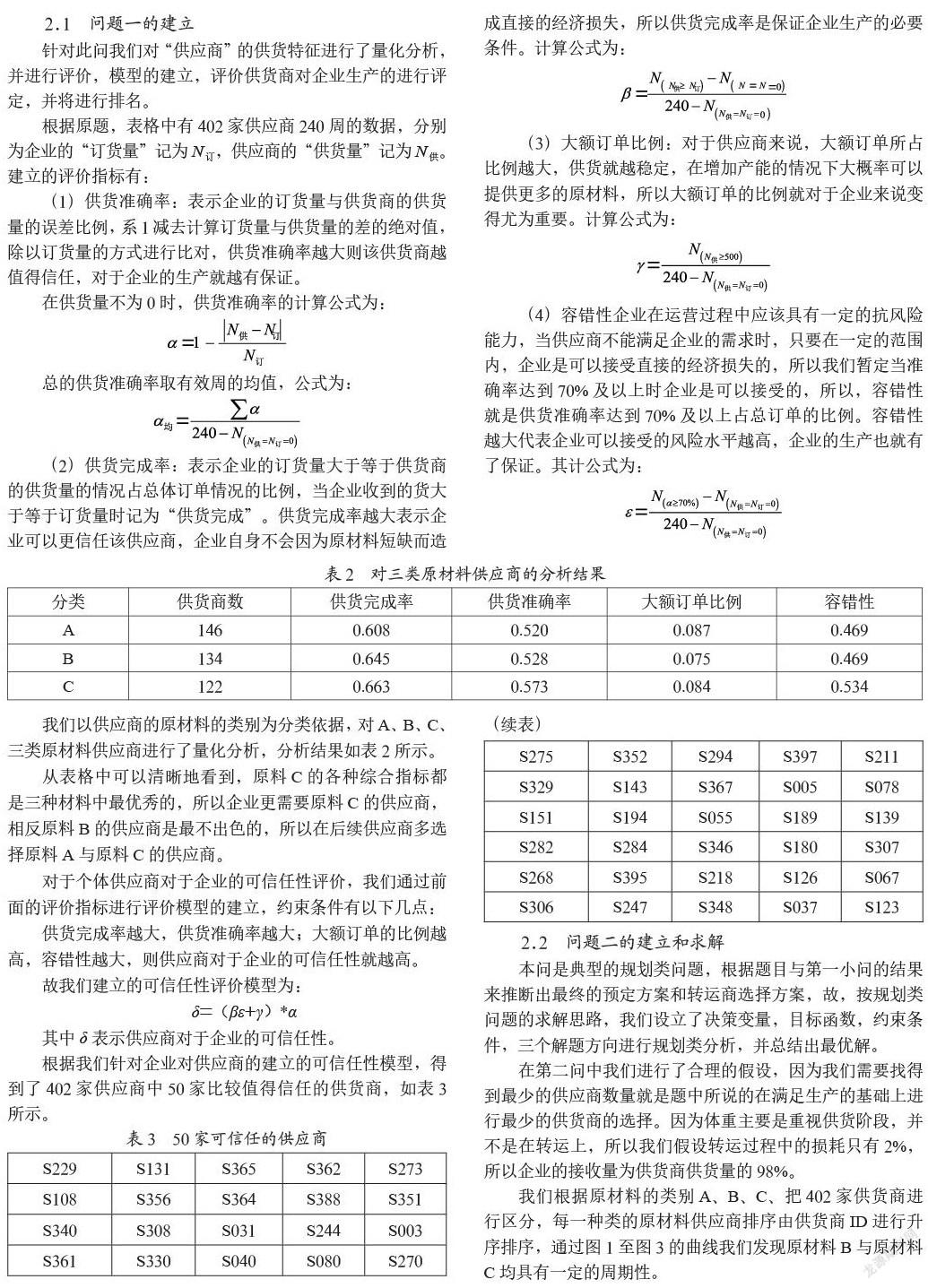
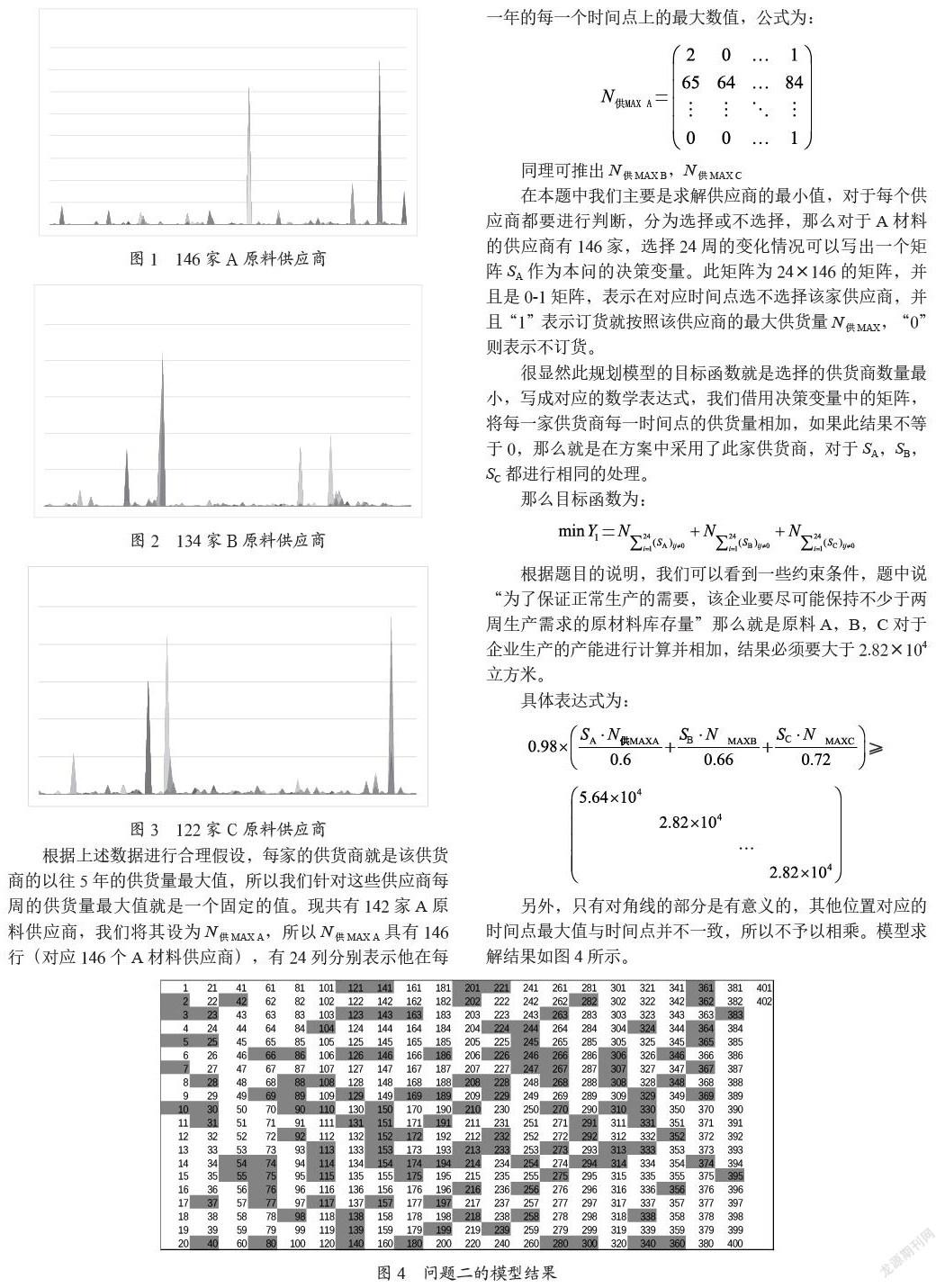
我们根据原材料的类别A、B、C、把402家供货商进行区分，每一种类的原材料供应商排序由供货商ID进行升序排序，通过图1至图3的曲线我们发现原材料B与原材料C均具有一定的周期性。

根据上述数据进行合理假设，每家的供货商就是该供货商的以往5年的供货量最大值，所以我们针对这些供应商每周的供货量最大值就是一个固定的值。现共有142家A原料供应商，我们将其设为N供MAX A，所以N供MAX A具有146行（对应146个A材料供应商），有24列分别表示他在每一年的每一个时间点上的最大数值，公式为：

同理可推出N供MAX B，N供MAX C

在本题中我们主要是求解供应商的最小值，对于每个供应商都要进行判断，分为选择或不选择，那么对于A材料的供应商有146家，选择24周的变化情况可以写出一个矩阵SA作为本问的决策变量。此矩阵为24×146的矩阵，并且是0-1矩阵，表示在对应时间点选不选择该家供应商，并且“1”表示订货就按照该供应商的最大供货量N供MAX，“0”则表示不订货。

很显然此规划模型的目标函数就是选择的供货商数量最小，写成对应的数学表达式，我们借用决策变量中的矩阵，将每一家供货商每一时间点的供货量相加，如果此结果不等于0，那么就是在方案中采用了此家供货商，对于SA，SB，SC都进行相同的处理。

那么目标函数为：

根据题目的说明，我们可以看到一些约束条件，题中说“为了保证正常生产的需要，该企业要尽可能保持不少于两周生产需求的原材料库存量”那么就是原料A，B，C对于企业生产的产能进行计算并相加，结果必须要大于2.82×104立方米。

具体表达式为：

另外，只有对角线的部分是有意义的，其他位置对应的时间点最大值与时间点并不一致，所以不予以相乘。模型求解结果如图4所示。

供应商的最少数量时对应的决策方案程序为：

clear all;

clc;

options = gaoptimset（‘Generations’， 1000，...     %设置迭代次数

‘PopulationSize’， 200）;     %设置种群

[x1，fval]=ga（@fitness1，402*24，[]，[]，[]，[]，zeros（402*24，1），ones（402*24，1），@nonlcon1，options）;

S = reshape（x1，24，402）;

xlswrite（‘供应商的最少数量时对应的决策矩阵.xlsx’，S）;

3  结  论

本文建立了一个具有一系列约束的非线性规划模型.利用MATLAB软件设计了遗传算法.模拟确定了每个供应商在每个周期内从每个供应商购买的每个制造商的数量。与启发式算法相比，制造商的成本显著降低，表明该算法可以联合优化多家厂商之间的订单分配。并且采用评价模型对指标进行加权，使结果更加明显，计算方法简便实用。

参考文献：

[1] 郑培，黎建强.基于BP神经网络的供应链绩效评价方法 [J].运筹与管理，2010（2）：26-32.

[2] 朱浩然.A公司供应链成本管控体系研究 [D].青岛：青岛科技大学，2020.

[3] 鲁宏浩，鲁玉军.基于分布估计—蚁群混合算法的柔性作业车间调度方法研究 [J].机电工程，2019，36（6）：568-573.

[4] 杨倩，胡燕海.基于遺传算法的多源多周期采购决策优化 [J].轻工机械，2020，38（2）：103-107.

[5] 戴卓.多周期多原料的供应链网络成本优化及其混合遗传算法 [J].计算机应用研究，2014，31（9）：2620-2624.

[6] 龙菲.供应中断风险下基于成本和服务的多源采购策略 [D].北京：北京交通大学，2016.

作者简介：张波（2001—），男，汉族，山西吕梁人，本科在读，研究方向：自动控制;梁哲（2000—），男，汉族，吉林松原人，本科在读，研究方向：自动控制;莫淇皓（2000—），男，汉族，浙江台州人，本科在读，研究方向：自动控制;马龙（1996—），男，汉族，河北邢台人，硕士研究生在读，研究方向：人工智能、群智能。