基于集合经验模态分解和奇异谱分析的曲线光顺算法
2021-01-14吴易泽
吴易泽,张 旭
(上海工程技术大学 机械与汽车工程学院,上海 201620)
0 引言
随着科技水平的不断进步,作为计算机辅助几何设计(Computer Aided Geometric Design, CAGD)中的一个重要分支,曲线曲面造型技术一直发挥着极其重要的作用,特别是在航空航天、船舶、汽车等对制造精度和外观有着较高要求的制造业领域。此外,曲线曲面造型技术对产品质量、物理性能等都将会有重要的影响。因此,曲线曲面造型技术受到工业界和学术界的广泛关注,并且一直是CAGD中的研究热点。
曲线的光顺算法种类很多。基于光顺效果可分为整体光顺和局部光顺[1];基于光顺原理可分为节点删除和节点插入;还有基于能量法的光顺和基于小波技术的光顺等。Farin等[2]提出一种B样条曲线光顺算法。Sapidis等[3]提出一种B样条曲线的自动光顺算法。龙小平[4]提出一种B样条曲线的局部能量算法。高斌等[5]提出一种基于曲率变化约束的平面B样条曲线光顺方法,通过曲率单调性约束条件,考虑曲线段的离散能量及原始曲线的误差控制,从而实现了曲线光顺。王士玮等[6]通过将曲线光顺问题建模成基于稀疏模型的优化问题,从而提出一种新的曲线光顺算法。
近年来,基于小波分析的曲线曲面光顺方法受到了国内外专家学者的广泛关注。Amati[7]提出了一种基于小波分析的曲线光顺算法。Wang等[8]基于小波分析,提出了非均匀有理B样条(Non-Uniform Rational B-Splines, NURBS)曲线曲面的光顺方法。赵罡等[9]针对一般的非均匀B样条曲线,提出了一种基于非均匀B样条小波的曲线光顺算法。
事实上,由于数字曲线与离散信号之间的相似性,可通过信号分析的方法来处理数字曲线的光顺性。显然,数字曲线是一种非平稳信号。处理非平稳信号的方法包括傅里叶变换、小波分析、Gabor展开等。上述方法虽然都能在不同程度上处理非平稳信号,但都有其局限性,无法从根本上解决傅里叶变换在信号分析中的问题。为解决该问题,Huang等[10]提出一种算法——经验模态分解(Empirical Mode Decomposition, EMD),成功地解决了这个问题。为有效地区分出复杂的非平稳信号中的信号和噪声,该算法自适应地将其从高频到低频分解成有限个本征模态函数(Intrinsic Mode Function, IMF)及一个残余项。
基于EMD方法,秦绪佳等[11]提出一种通过构造近似均值曲线并以此将原始曲线进行一维参数化的光顺方法。谭小俊等[12]提出一种双变量EMD分析的平面离散曲线光顺方法,取得了不错的光顺效果。可是这些方法仅去除了一次EMD分解后所得的IMF分量或多次EMD分解后所得的多个IMF分量,去除的干扰的IMF分量中可能含有有效的特征信息,保留下的IMF分量也可能含有噪声信息,且分解的次数需要根据特定的曲线设定。此外,EMD分解还存在某些不足,如端点效应、模态混叠。
针对EMD方法存在的不足之处,Wu等[13]提出一种算法,即集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD),成功地弥补了该算法的不足,也即EEMD方法能完美避免尺度混合,并能使最终分解的IMF分量保持物理上的唯一性。基于此,本文考虑将EEMD方法应用于曲线光顺,若对EEMD分解后的若干个分量逐一进行降噪处理,在增加工作量的同时,还会降低光顺效果,并且会增大误差。因而本文提出采用游程检测法重构EEMD分解后的分量,将其重构为高频分量和低频分量。此时噪声主要集中在高频分量,单独去除高频分量在产生较大误差的同时,会去除曲线的有效特征。由于奇异谱分析(Singular Spectrum Analysis, SSA)方法在非线性、非平稳信号的分析方面,属于一种有效的分析方法,它可以显著地降低信号中的噪声,有效地提高信噪比[14-15],并能保留噪声信号频带相混叠的有用信号,突出信号的信息特征。因此,本文采用奇异谱分析对高频分量进行降噪处理,在一定程度上保留了曲线的有效信息,避免了曲线光顺后的拟合误差过大。试验表明,本文提出的EEMD分解、游程检测法重构和SSA降噪三者相结合的方法对曲线具有很好的光顺性。
1 算法原理
1.1 EMD与EEMD算法
EMD是由Huang等[10]提出的处理非平稳和非线性信号的信号处理方法,该方法可将复杂的原始数据信号按不同尺度从高频到低频自适应地分解成若干个IMF分量和一个剩余分量Res。
EMD分解是一个“筛选”信号的过程,其详细分解步骤参考文献[16-19]。分解后的每个IMF分量需满足两个条件:
(1)对于任意分解得到的IMF分量中,过零点、极值点的个数之差小于等于1;
(2)由局部极大值点、局部极小值点分别确定的上、下包络线均值为0。
EEMD作为一种信号处理算法,其在非线性信号、非平稳信号的分析处理上具有举足轻重的地位,能够利用噪声特性有效地克服由于EMD方法容易产生模态混叠现象的问题[13]。该方法本质上是对添加了高斯白噪声的信号进行多次EMD分解,同时利用高斯白噪声的随机性,可以经过反复试验降低相应的IMF分量的模式混叠程度。该方法的具体分解步骤如下:
(1)将高斯白噪声n(t)添加到目标信号y(t),得到一个新的信号x(t):
x(t)=y(t)+n(t)。
(1)
式中,高斯白噪声n(t)服从下式:
(2)
式中,ε为噪音强度参数;N为总体个数;εn为信号的标准差。
(2)按照EMD分解方法对信号x(t)进行分解,得到1组IMF分量ci(t)和1个余量r(t):
(3)
式中n为IMF分量个数。
(3)重复步骤(1)和步骤(2),每次添加不同的白噪声nj(t),得到M组IMF分量和剩余分量。
(4)利用高斯白噪声频谱的零均值原理,将分解出的M组IMF分量和剩余分量的整体平均值作为最终结果,目标信号对应的IMF分量ci(t)可表示为:
(4)
1.2 游程检测法
游程检测亦称“连续性检验”,是一种利用游程总数来判断样本随机性的统计检验方法[20-21],其中游程是指样本序列中连续出现的变量值的次数。

(5)
式中,st由一组相互独立统计的随机分布的“0-1”序列组成,将每段连续相同符号(0或1)的序列定义为一个游程,将每一段游程中的数据个数定义为一个游程长度。
在游程检测法中,可以根据游程总数的大小判断出对应的EEMD分量的波动程度。进而,依据游程检测法设定高频、低频分量的游程阈值和游程长度阈值。若游程总数大于阈值,同时游程长度较短,此时序列变化较大;反之,游程总数小,同时游程长度长,此时序列变化小。在每个分量的游程数和游程长度经过综合考量之后,EEMD分解后的分量被重构为高频、低频两种分量。
1.3 奇异谱分析算法
1978年,Colebrook提出了奇异谱分析算法,它是一种主成分分析方法[22]。由于其时效性强、计算简单,非常适用于非线性、非平稳信号的处理[23]。
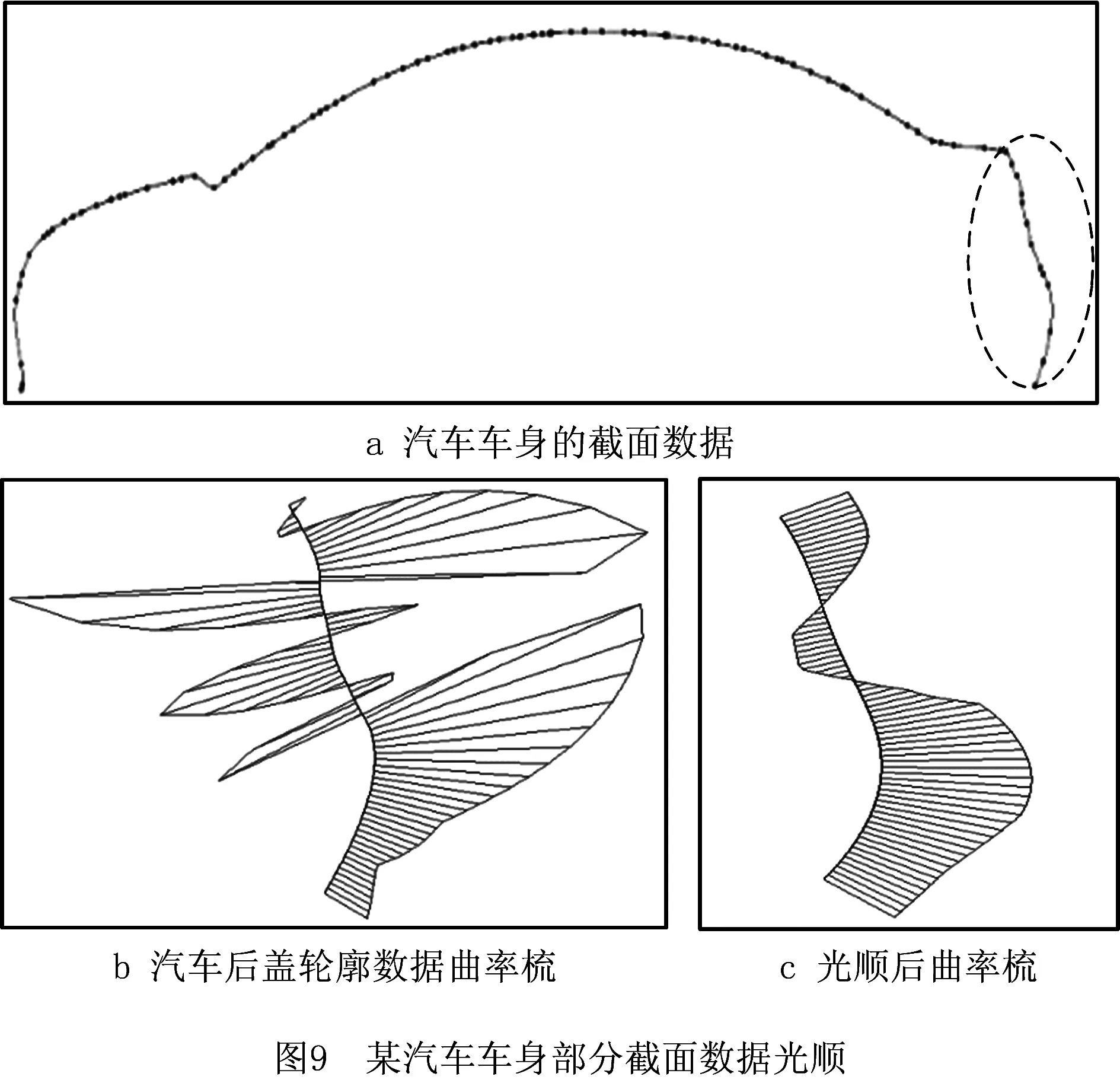
假设有某一一维信号x(i)(i=1,2,…n),给定嵌入维数为m(m (6) 令S为时滞矩阵的m×m维协方差矩阵,则 (7) 采用奇异谱分析对协方差矩阵S进行分解,从而得到m个奇异值λi(i=1,2,…,m)。为了将该信号的奇异谱图构造出来,通过将得到的m个奇异值进行降序排列λ1>λ2>…>λm≥0。其中,奇异值大小表示信号和噪声在奇异谱图中能量大小的相对关系。将值较大的奇异值点看成信号点,而将值较小的奇异值点看成噪声点。λk对应的特征向量Ek称作经验正交投影函数,采样信号x(i)在特征向量Ek上的正交投影系数就是第k个主分量: (8) 如果已知各主分量与经验正交函数,反求原始信号序列的过程如下: (9) 在曲线的光顺过程中,首先将空间离散数字曲线的x,y,z三个变量视为3个一维数字信号;其次对每个变量的数字信号序列分别进行EEMD分解,将每个变量分解成多个IMF分量和一个Res余量;接着分别对每个变量分解后的所有分量使用游程检测法,将其重构为高频、低频分量;随后对重构后的高频分量使用SSA进行降噪;最终将降噪后的高频分量与低频分量进行重构,进而得到光顺后的曲线。其曲线光顺流程图如图1所示。 具体步骤如下: (1)原始数字曲线信号的EEMD分解。将空间离散数字曲线的x,y,z三个变量视为3个一维数字信号,然后对每个变量的数字信号序列分别进行EEMD分解,将其分解成n个具有不同特征的IMF1~IMFn分量和一个Res余量。 (2)由于在EEMD分解中,得到了数量相对较多的IMF分量,若对每个分量逐一进行降噪处理,会去除曲线的有效信息,同时会加大光顺工作量和增加曲线光顺的误差,这就需要对每个变量的序列分量进行重构。其重构步骤如下: 1)计算游程数、最大游程长度。计算每个变量所有的IMF分量、Res余量的游程数以及与之相对应的最大游程长度; 2)确定阈值。根据每个分量的游程数和最大游程长度,选择游程数变化率最大的游程数作为阈值; 3)划分高频、低频分量。比较阈值与每个分量的游程数,得到高频、低频分量; 4)根据判断结果,对x,y,z三个变量的各个分量分别进行叠加,最终得到重构后的高频、低频分量。 (3)奇异谱分析降噪。对进行游程检测法后得到的高频分量进行奇异谱分析降噪。在奇异谱分析降噪的过程中,重构信号时阶次p的选择是一个重要环节。其降噪步骤如下: 1)使用Cao方法[24]确定最小嵌入维数m(本文选取m=40),同时构建时滞矩阵X; 2)构建矩阵X的m维协方差矩阵S,对其进行奇异值分解,从而得到m个奇异值; 3)确定信号的奇异谱图,并将奇异值按降序排列,从而确定信号的奇异谱图; 4)选取主分量作为重构后的高频分量,其中,主分量的重构主要选取前面几个奇异值较大的点。 (4)光顺结果重构。将降噪后的高频分量与低频分量进行重构,最后得到光顺后的曲线。 (5)光顺结果分析。采用3种不同的曲线光顺算法进行光顺性结果对比。采用曲率图作为评价指标。曲率图中曲率变化平稳,说明曲线光顺;曲率变化变化大,说明曲线不光顺。其中,曲率计算公式为: k= (10) 根据1.1节所述的EEMD分解步骤,对空间离散曲线上的x,y,z三个变量分别进行EEMD分解。通过查阅文献[10],本文所选取的曲线离散数据点个数为100,则原始数据点分解为100组IMF分量,故设置M=100,α为显著性水平,一般设α=0.25,ε为噪音强度参数,取值范围为(0~1),由于数据点个数较少,取值为1/4,故设ε=0.25。 EEMD分解步骤完成后,最终x变量的时间序列被分解成5个IMF分量和1个剩余分量Res;y变量的时间序列被分解成5个IMF分量和1个剩余分量Res;z变量的时间序列被分解成5个IMF分量和1个剩余分量Res。其原始曲线及其分解结果如图2所示。 观察图2可以发现,空间离散数字曲线的x,y,z三个变量序列的非线性、非平稳性特性相当明显。其中,IMF1~IMF5分量分别反映了离散数字曲线的数据点序列在不同频率上的变化信息,余项Res则展示出曲线在光顺后的变化。 由于各个变量经过EEMD分解后,得到的分量过多,各个变量上的噪声在每个IMF分量上分布不均,且在IMF1~IMF5以及Res上噪声呈现由高到低的趋势。因此,在对所有分量进行降噪处理之前,需要先对其进行游程检测法重构,得到高频分量和低频分量。 分别对x,y,z三个变量的5个IMF分量和1个Res余量使用游程检测法,将得到3个变量序列的游程数、最大游程长度,结果如表1所示。 表1 分量的游程数与最大游程长度 续表1 分析表1,综合考虑游程数和最大游程长度,设游程数的阈值为10,设最大游程长度的阈值为50,将游程数大于10且最大游程长度小于50的分量合并为高频分量,反之则合并为低频分量。 最终得到x变量的高频分量由IMF1~IMF5叠加而成,x变量的低频分量由Res叠加而成;将y变量的IMF1~IMF4叠加为其高频分量,IMF5和Res叠加为其低频分量;z变量的IMF1~IMF4叠加为其高频分量,IMF5和Res叠加为其低频分量。最后重构得到x,y,z三个变量的高频分量和低频分量,如图3所示。 由3.2节所述可知,数据噪声主要集中在高频分量。因此,对高频分量进行降噪处理是必不可少的。由于在信号降噪中SSA的效果较优,若对含噪数据运用SSA降噪,如果信号重构阶次过大则会残留大量噪声,反之会损失有效数据信息。因此,SSA信号重构阶次的选择是个关键问题,合适的阶次可以很好地保留有效数据,反之不合适的阶次则会导致数据信号失真或者噪声过多。重构阶次的选择有多种,通过对比,本文最终使用奇异谱构造三角形求余弦值的方法确定重构阶次,进而重构数字变量,具体步骤参考文献[25]。 根据余弦定理公式,对其变形得: 式中:a为三角形的第一个边长;b为三角形的第二个边长;c为三角形的第三个边长;C为边长c所对的角。 众所周知,在[0,π]上,余弦函数单调递减,因此最大的余弦值对应着最小的角。因此,拐点位置即为最大的余弦值所处的位置,即重构阶次p值。通过连接首尾奇异值、中间奇异值,构建三角形,如图4所示。 分析图4可知,图中特征值按照降序排列,横、纵坐标轴分别表示奇异值个数、与之相对应的奇异值,图中奇异值按照降序排列。正常情况下,将图4中奇异值趋于平坦的部分认定为噪声奇异值,因此,由较大的奇异值组成了变量的主要成分,小的奇异值组成了噪声。由此可知,x,y,z高频分量的重构阶次如表2所示。 表2 重构阶次P值的选取 选取前p个奇异值进行信号重构,计算公式如式(12)所示: (12) 得到降噪后的高频分量,如图5所示。 在验证本文算法有效性的同时,选取2种典型算法与本文算法一起对同一条曲线进行对比试验。3种优化算法的光顺结果如图6所示。 本文所选取的2种典型的光顺方法分别为EMD法和曲率法。其中,EMD法是通过EMD分解原始曲线数据,得到频率不同的IMF分量,去除高频分量,保留低频分量,最终得到光顺后的曲线,该算法是从数据实际出发来对数据进行处理;曲率法是通过曲率变化图使目标曲线曲率单调均匀变化的曲线光顺方法,该算法是从曲线的光顺准则出发来对曲线进行处理。 观察图6可知,相比于EMD法、曲率法,从曲线光顺效果上看,本文算法效果最优。其中,在曲线拐点处的光顺处理上,本文算法比EMD法、曲率法的光顺效果更好。因此,初步观察,直观上可知本文提出的算法具有一定的优势。 为进一步验证本文算法的有效性,算出原始曲线的曲率以及各个方法的曲率,其曲率图如图7所示。 分析图7可知,本文提出的光顺方法所得的曲线曲率变化最为平缓,且曲率值较低。本文方法与EMD法相比,光顺效果略优,与曲率法相比,优势较为明显。 为了更加客观地评价3种方法的优劣性,现计算出各个曲线的曲率值,其曲率结果分析如表3所示。 表3 各方法曲率结果分析 分析表3可知:从最大曲率上看,本文算法所得最大曲率最小,比原始曲线小了2.426 1,比EMD方法小了0.242,比曲率法小了0.100 5;从最小曲率上看,本文算法所得最小曲率最大,比原始曲线大了0.010 4,比EMD法大了0.009,比曲率法大了0.006;从平均曲率上看,本文算法所得平均曲率最小,比原始曲线小了0.076 1,比EMD法小了0.002 6,比曲率法小了0.021 9。综合分析最大曲率、最小曲率和平均曲率可知,本文算法在保留曲线有效特征的同时,也有效地去除了曲线的噪声。相比之下,本文算法的光顺效果最优。 从运行时间上看,EMD法运行时间最短,本文算法次之,曲率法运行时间最长。本文算法运行时间虽慢于EMD法,但本文方法是多次EMD方法的叠加,因此其运行时间慢于EMD法。虽然运行效率略低,但曲率值变化更为平缓,效果更优。 表3虽然对上述3种方法的曲线曲率进行了对比,但本文算法仅针对曲线进行光顺,相反曲率法还可以针对曲面进行光顺,因此,本文算法还存在一些局限,只能对曲线进行光顺。 为了进一步验证本文算法,了解本文算法在工程实际中的应用,现给出以下3个实例分析。 实例1图8是带噪声的离散数据光顺,它是在图8a的模拟数据中加入了高斯噪声。图8a为局部加入了0.02 mm的高斯白噪声的初始截面数据;图8b是经由本文算法处理后得到的光顺结果。观察图8可以发现,经由本文算法处理后,加入高斯噪声的模拟数据取得了不错的光顺效果。 实例2图9为某汽车车身部分截面数据的光顺,在验证本文算法的重构及光顺效果有效性的过程中,选择图9a中画虚线内的汽车后盖轮廓截面数据作为验证的原始数据。图9a是汽车车身的截面数据。图9b是汽车后盖轮廓截面数据的曲率梳。观察图9,通过对比汽车后盖处理前后的曲率梳图,显然,经由本文算法的处理,汽车后盖得到了很好地光顺。 实例3图10为某涡轮叶片榫头部分截面数据的光顺,在验证本文算法的重构及光顺效果有效性的过程中,选择图10a中画虚线内的部分榫头截面数据作为验证的原始数据。图10a为涡轮叶片榫头的截面数据,数据采集密度D≤0.02 mm。图10b为涡轮叶片榫头部分数据的曲率梳图,图10c为本文方法光顺后的曲率梳图。观察图10可以看出,经过本文算法的处理,涡轮叶片榫头得到了相应程度地光顺。 本文利用集合经验模态分解、游程检测法重构和奇异谱分析降噪三种方法相结合,提出一种将空间离散数字曲线看成离散数字信号的曲线光顺算法,其核心部分在于: (1)使用EEMD对空间离散数字曲线进行多尺度分解,一方面解决了EMD分解后出现的边界效应和模态混叠问题;另一方面有效降低了原始空间离散数字曲线的x,y,z三个变量序列之间的相互干扰,以及有效降低了其非平稳性;同时较为深入地挖掘了空间离散数字曲线的信息。 (2)由于EEMD分解时,所得到的分量过多导致光顺工作量变大,采用了游程检测法重构EEMD分解后的分量。在减少计算量、降低误差的同时,可以更加直观地反映原始空间离散数字曲线的特征。 (3)在对重构后的分量进行处理时,考虑到原始空间离散数字曲线的噪声主要集中在高频分量,直接删除高频分量会去除曲线的有效信息,采用了SSA对高频分量进行降噪,从而避免了去除曲线的有效特征,使得曲线的光顺尽可能符合原始曲线。 本文算法还存在一些不足:①在EEMD分解中,虽然在一定程度上克服了边界效应和模态混叠的问题,但未能彻底解决;②在使用SSA降噪过程中,仅对高频分量去噪。然而在实际情况中,还有一些噪声存在于低频分量中,本文未对其进行处理,致使光顺后的曲线中还存留一些噪声信息,采取何种方法对低频分量进行处理,这是本文以后研究的方向。
2 光顺过程
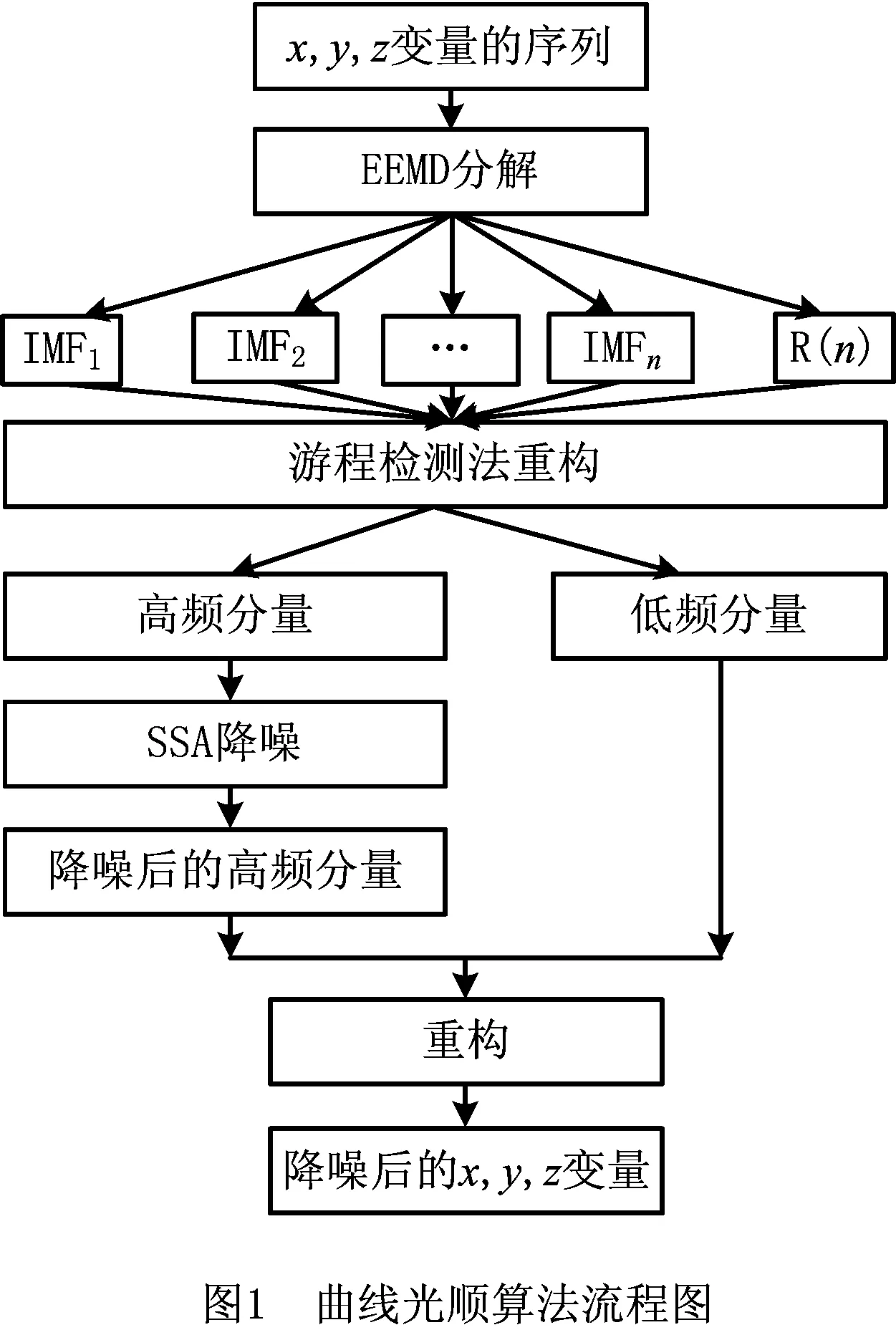
3 试验与结果分析
3.1 基于EEMD的空间离散曲线上的x,y,z三变量分解

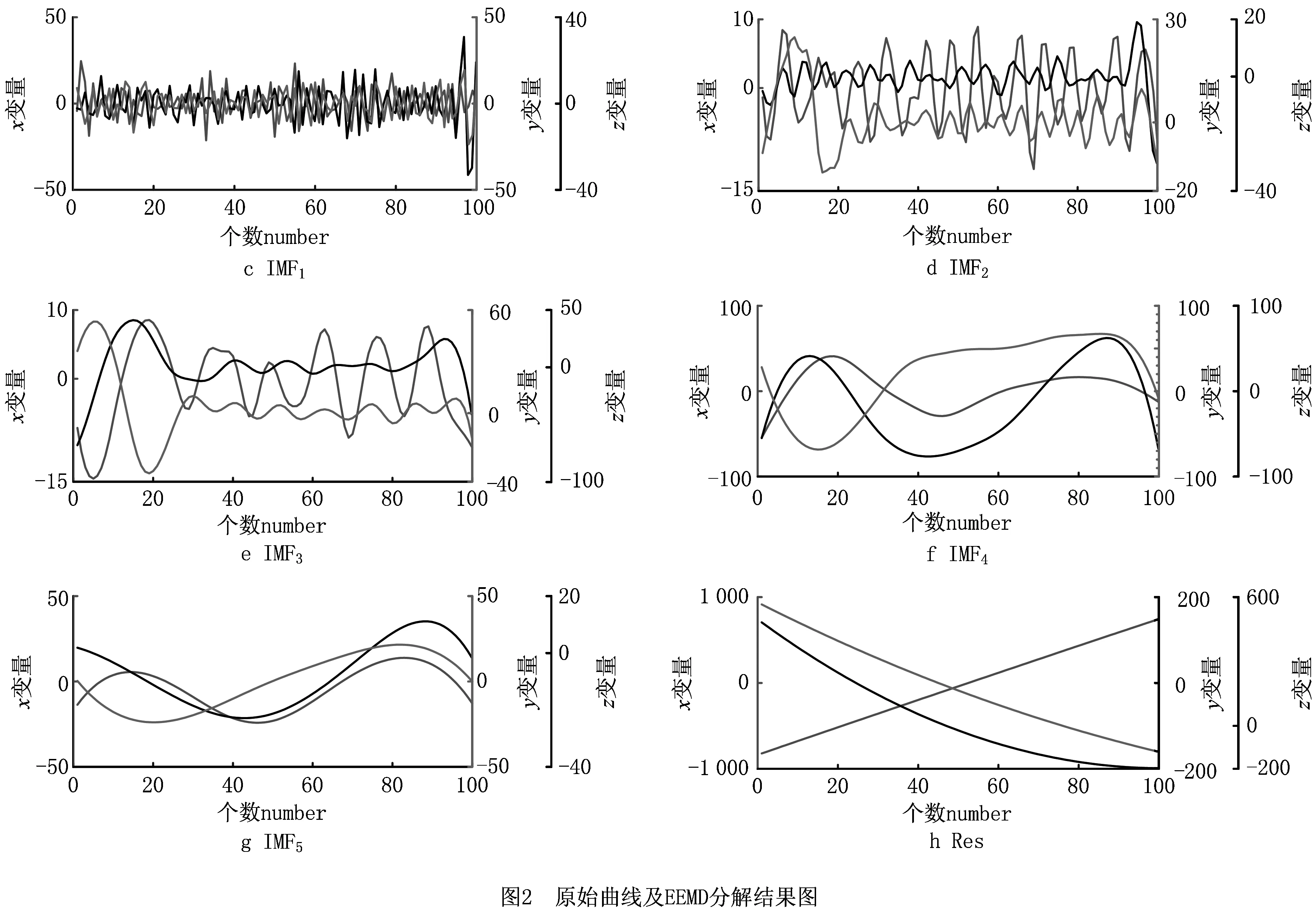
3.2 游程检测法重构




3.3 奇异谱分析降噪
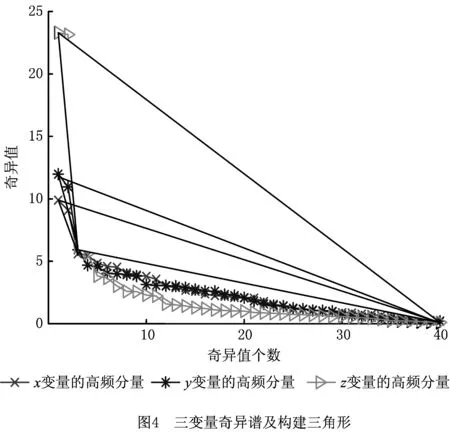


3.4 光顺结果与对比分析
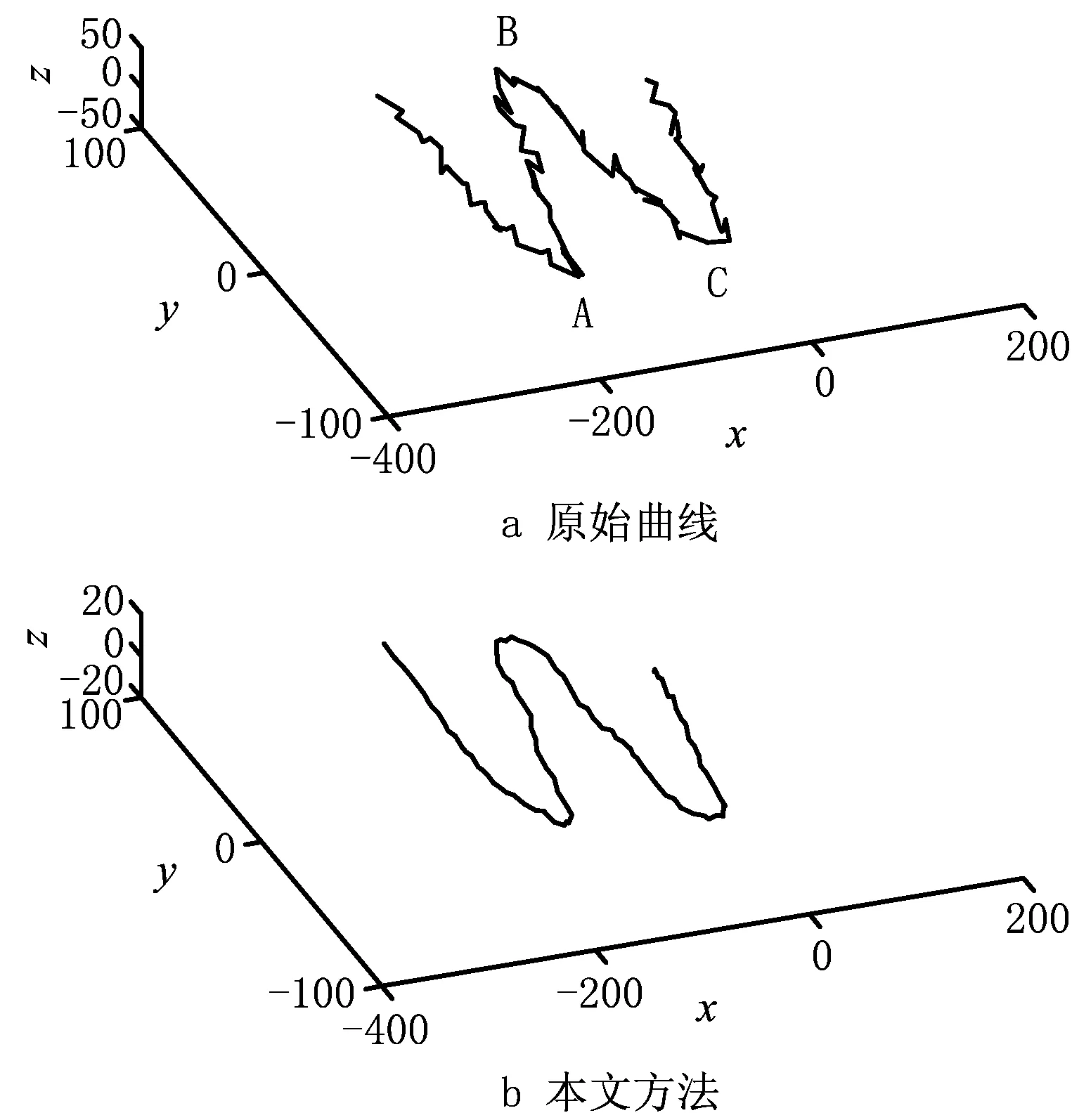



4 实例分析


5 结束语
