基于改进多目标灰狼算法的装配线平衡与预防维护集成优化
2021-01-14唐秋华张子凯卢辰灏邓明星
蒙 凯,唐秋华+,张子凯,卢辰灏,邓明星
(1.武汉科技大学 冶金装备及其控制教育部重点实验室,湖北 武汉 430081;2.武汉科技大学 机械传动与制造工程湖北省重点实验室,湖北 武汉 430081;3.东风雷诺汽车有限公司设备保全科,湖北 武汉 430056;4.武汉科技大学 汽车与交通工程学院,湖北 武汉 430081)
0 引言
装配线平衡和设备维护是保证整条装配线高效运行的两个独立子系统,即在生产进行之前,利用装配线平衡确保整条装配线上各工位的负载均衡,以更好地发挥装配线生产效率;设备维护是按规定计划或技术规程进行的设备管理活动,设备维护常分为故障维护与预防维护,旨在控制设备性能劣化或降低设备失效概率。由于装配线平衡和设备维护的相对独立,在现行装配生产中逐渐表现出以下两个问题:
(1)由于装配线平衡是在假定所有工位都正常工作的前提下做出的,且装配线上各工位具有串行流水特征,当其中一个工位突发故障或任一工位上设备需要维护时,必然要求整条装配线停工。其中未发生故障或不需要维护工位的被迫停机,自然导致产能的巨大浪费和成本的巨幅提升。
(2)故障维护是在设备出现故障后的事后维护,预防维护是为确保设备工作状态的提前性维护,装配线平衡是在生产进行之前的计划性任务分配。从时间上来说预防维护和装配线平衡都需要提前进行。但是两者的目标不一致,常发生时间冲突。装配线平衡的目标是使整条装配线快速高效运转,预防维护目标是设备的可靠性或可用度高。当生产任务或设备维护任务很重时,如何协调工位维护时间或装配生产时间,避免两者之间的时间冲突,目前还缺乏有效依据。
据此,需将装配线平衡与工位设备预防维护进行集成优化,制定出能提供设备维护契机、保证维护时生产连续性的多套分配方案。在正常生产过程中,如果某工位设备需要进行预防维护,可按照预先制定的生产计划,快速从一套分配方案切换到另一套方案。通过生产的快速调整,提升生产时的设备可维护性和维护时的生产连续性,避免因设备维护造成整线停机所致的生产损失,而且对提高工位利用率和缩短产品制造周期,也具有重要意义。
在已发表文献中,还未见将装配线平衡与工位预防维护集成优化的研究,然而在装配线平衡、预防维护和生产调度与预防维护集成优化等相关领域,具有很多研究基础。首先在装配线平衡方面,根据所优化目标的不同,将问题分为3类:第Ⅰ类问题给定节拍,优化工位数量[1];第Ⅱ类问题给定工位,最小化节拍[2-3];第Ⅲ类问题给定节拍和工位,最大化生产线效率。装配线平衡与工位预防维护的集成优化,实质上是在工位给定情形下最小化多重生产节拍与生产调整,可算是第Ⅱ类问题的变体。
关于设备预防维护,方玲珍等[4]以单位维护成本的产出最大化为优化目标,构建了一种维护效率导向的设备预防维护模型。Seiti[5]等提出一种表达模糊可靠性的新模糊模型,并考虑了可能因素的风险和误差,将其用于多期时间范围内的预防维护计划。但对平衡与维护的集成优化问题而言,上述问题仅考虑了设备预防维护,并不能实现维护时连续生产的目标。
生产调度与预防维护的集成优化,目前仅在加工车间、流水车间等方面有相关研究。如蒋凯丽等[6]等针对两阶段的混合流水线系统,考虑具有时间窗的周期性维护需求,以最小化最大完成时间为调度指标,建立调度与维护的联合优化模型。Adrian[7]等提出一种基于中期优化的方法,用于将生产计划、调度和维护进行集成。然而,目前文献还未见考虑无缓冲前提下装配线上设备预防维护与线平衡的集成。
为求解具有强NP-hard属性的组合优化问题,近期出现了很多新颖的智能优化算法,如灰狼优化算法[8]、鲸鱼优化算法[9]、蝗虫优化算法[10]等。其中,灰狼优化算法通过模拟狼群觅食过程,借助头狼的导引能力和普通灰狼的自适应调整能力,实现全局寻优,主要优点是:①结构简单、需要调节的参数少、容易实现[11];②存在能够自适应调整的收敛因子以及信息反馈机制,能够在全局搜索与局部寻优之间实现平衡,在问题求解精度和收敛速度方面都有良好的性能[11]。该算法已在无人作战飞行器路径规划[12]、经济调度指派[13]、直流电机最优控制[14]、多输入输出电力系统[15]等诸多领域得到成功应用。并且,算法虽主要用于求解连续优化问题[11],但在离散问题中同样有效[16]。
因此,针对装配线平衡与预防维护的集成优化问题,首先需要面向正常生产和给定工位预防维护等多种情形,构建可实现多套装配线平衡方案且各方案之间调整代价小的多目标优化模型。其次,考虑到装配线平衡与预防维护的集成优化问题特点,需要设计一种改进的多目标灰狼算法(Improved Multi-Objective Grey Wolf Optimization algorithms, IMOGWO),并通过对比实验验证算法的合理和有效性,以便经济、高效地求取较优解。
1 问题描述
在装配线平衡与预防维护的集成优化时,需要考虑多种生产情形:①正常工作,即装配线上每个工位均能正常生产;②指定工位设备预防维护,即根据设备可用性、可靠性等的预测,推断在未来一段时间内需要进行预防维护的设备及工位,每一种预防维护情形下需要停机的工位不同。当二者集成后,生产过程就变成多种生产情形之间的切换,以便实现高效生产、满足设备维护要求。考虑到设备维护的频率,后续生产调整主要指在正常工作与预防维护情形之间的变动,不考虑多种预防维护情形之间的变动。其中涉及到的符号及其说明如表1所示。

表1 符号及其说明
1.1 多目标优化模型
包含两类目标:
(1)最小化各生产情形下的节拍,包括正常工作和各种预防维护情形。其中,所考虑生产情形的总量即为该类型优化目标的个数。
minCTc∀c∈C。
(1)
(2)最小化正常工作与各种预防维护情形间的工序调整数。工序调整即将一个操作从一个工位调整到另一个工位,涉及到对应物料的调整、操作工技能/工夹具等的调整,影响生产现场稳定性,也会扰乱生产秩序。优化工序调整数量,对于快速实现生产切换、快速恢复工作秩序,具有显著意义。
c∈{2,…,C}。
(2)
1.2 约束
集成考虑装配线平衡与工位预防维护,还需考虑各种情形下的约束,包括工位分配约束、工序分配约束、节拍约束、优先关系约束等。
(1)工位分配约束 正常工作时,每个工位都应该被分配工序,且至少完成一个工序。但当进行工位维护时,需要维护的工位不被分配工序。
(3)
(4)
(2)工序分配约束 在任何生产情形下,每个工序都必须分配到工位中,且只能分配一次。
(5)
(3)节拍约束 正常工位的总操作时间不能超过节拍,处于维护情形下工位的总操作时间为0。
(6)
(7)
(4)优先关系约束 当某道工序的所有前序工序都已经分配完毕时,该工序才能分配。
(8)
式(1)~式(8)综合反映出平衡与维护集成优化问题,本质上是一种带有多种整数决策的多目标优化问题。关于决策变量数,有多少种生产情形就需要多少套生产方案;而关于优化目标数,其数值为生产情形数加1,即式(2)表示的工序调整数。
2 改进多目标灰狼优化算法(IMOGWO)
2.1 基本灰狼算法
灰狼算法最早由Mirjalili等[8]于2014年提出,通过在29个标杆案例中与粒子群算法、引力搜索算法进行比较,证明了算法在对解空间的探索、避免局部最优、收敛性等方面都具有明显优势。灰狼算法通过模拟灰狼寻找猎物的行为搜索最优解,该过程可表示为:
D=|C×Xp(t)-X(t)|,
(9)
X(t+1)=Xp(t)-A×D。
(10)
其中:Xp表示猎物的位置;X表示任一灰狼的位置;t表示迭代次数;D表示灰狼与猎物之间的距离。亦即,任一灰狼在下一次迭代时的位置需根据猎物位置和相对距离确定。而A和C的计算公式如下:
A=2a×r1-a,
(11)
C=2×r2。
(12)
其中:r1、r2为[0,1]之间的随机数;a是一个线性减小的正数,初值为2。每次迭代开始时,用a减去初值与迭代次数t的商后赋值给a,最后一次迭代时,a为0。
灰狼社会有4种狼:α、β、δ和ω,其中,具有最佳目标函数值的灰狼称为α,具有第二、第三目标函数值的灰狼分别称为β和δ,其余灰狼称为ω[16]。普通灰狼ω的捕食行为常常由α个体进行引导,β、δ偶尔也引导狼群捕食。由于不知道最佳的猎物位置,为了从数学上模拟灰狼的捕食行为,可假设α、β、δ对猎物的潜在位置有更好的理解,再据此调整普通灰狼ω的位置。故而,基于式(9)和式(10),普通灰狼ω的捕食行为可以描述为:
Dα=|C1×Xα-X|,Dβ=|C2×Xβ-X|,
Dδ=|C3×Xδ-X|,
(13)
X1(t+1)=Xα(t)-A1×Dα,
X2(t+1)=Xβ(t)-A2×Dβ,
X3(t+1)=Xδ(t)-A3×Dδ,
(14)
(15)
其中X1、X2、X3分别为在灰狼α、β、δ引导下普通灰狼ω的位置分量。
2.2 基于随机键的编码、解码及目标函数值计算
平衡与维护集成优化问题主要涉及工序分配Xijc,采用灰狼算法优化时每个灰狼个体的编码也应该反映工序分配。由于该集成问题本质上是离散优化问题,而灰狼算法主要用于解决连续优化问题,故采用随机键的编码方式实现离散问题向连续问题的转化。限于篇幅,下述案例中仅考虑正常工作情形和一种工位预防维护情形。
在编码过程中,每个个体的编码包含两部分,共2×I个要素,前I个要素代表正常工作情形下的编码,第I+1~第2×I个要素代表工位维护情形下的编码。每个要素是介于(0,1)之间的随机数,且每一位置的随机数代表对应工序的权值。如图1所示的工序具有11个操作,每个工序加工时间分别为{6,2,5,7,1,2,3,6,5,5,4},考虑正常工作和一种维护情形的集成问题,其编码可表示为:{0.97,0.96,0.49,0.80,0.14,0.42,0.91,0.79,0.96,0.66,0.04|0.85,0.93,0.68,0.76,0.74,0.39,0.66,0.17,0.71,0.03,0.28}。
在上述编码基础上,需要进行进一步的解码,得到两种情形下的工序安排,步骤如下:

步骤2对于每种工作情形,依据随机键编码和工序间优先关系生成该情形下的加工序列。将直接前序已完成的全部工序,放入到待加工工序集中。在该集合中找到编码值最大的工序,置入到加工序列中;并将新的直接前序已全部完成的工序,增加到待加工工序集中。依次类推,直到所有工序都被加入加工序列。
步骤3针对正常工作情形,依据该情形下的加工序列,以CT1为节拍将装配操作分配至[1,J-1]工位中;将余下操作全部放入J工位,若能满足节拍约束,则转步骤4;否则,CT1=CT1+1,转步骤3,重新对工序进行分配。
步骤4针对指定工位需要维护的情形,依据该情形下的加工序列,以CTc为节拍将装配操作分配至除待维护工位和最后一个工位之外的其他工位中。若余下操作能全部放入最后一个不需维护的工位,且能满足节拍约束,则转步骤5;否则,CTc=CTc+1,重新执行步骤4。
步骤5分别输出正常工作和指定工位维护情形下的工序分配结果及节拍CT1和CTc,并计算工序调整数。
根据前述的随机键编码和优先关系图,生成正常工作情形下的加工序列。如图1所示,由于工序1没有紧前工序,将工序1直接放入加工序列;将工序{2,3,4,5}放入待加工工序集中。考虑其编码值分别为(0.96,0.49,0.80,0.14)且工序2数值最大,选择工序2进入加工序列。依次类推,可得到正常工作与预防维护情形下的工序分配序列各为{1,2,4,3,6,8,10,5,7,9,11}和{1,2,4,5,3,7,9,6,8,10,11}。在正常工作情形下,当CT1=13时,4个工位的工序分配顺次为:{{1,2},{4,3},{6,8,10},{5,7,9,11}}。预知工位3需要维护,且当CTc=16时,其余3个工位的工序分配顺次为:{{1,2,4,5},{3,7,9,6},{},{8,10,11}}。

在解码时已经获得不同生产情形下的节拍,还需计算工序调整数。总工序调整数PC定义为各预防维护情形与正常生产情形之间各工序所在工位差的绝对值之和。如图1所示,工序4在两种情形下分别被分配至工位2、工位1,故工位差绝对值为1。通过计算得到了每只灰狼对应的多个目标函数值,基于此还需对多个灰狼个体进行评价,选择优秀个体引导进化。
2.3 狼群等级划分与引导狼确定
原始灰狼算法让目标函数值最佳的灰狼α、β、δ引导其他灰狼进行捕食,从而实现位置更新。但在多目标问题中,仅在一个目标上进行比较,无法得到最优解,也无法选出α、β、δ。在以往的研究中,Mirjalili[17]等改进灰狼算法,实现灰狼算法求解多目标问题。为了更好地优化多目标问题,提出基于Pareto层级的狼群等级划分方法,并引进式(16)所示的拥挤距离[18],以计算同层灰狼个体之间的紧密程度:
(16)
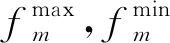
狼群等级划分方法如下:按Pareto层次构造方法对狼群个体进行分层,选出非支配灰狼个体作为第一层,然后在剩下的灰狼个体中选出非支配个体作为第二层。以此类推,直到所有灰狼都被分层。然后按照式(16)计算每层灰狼个体间的拥挤距离。
在确定引导狼α、β、δ时,可分为以下4种状况:①若第一和二层灰狼个体数都为1,将第一层灰狼个体定为α,第二层灰狼个体定为β,然后在第三层中选择拥挤距离最大的个体作为δ;②若第一层灰狼个体数为1,第二层灰狼个体数大于1,将第一层灰狼个体定为α,然后选择第二层中拥挤距离最大的两个个体作为β、δ;③若第一层灰狼个体数为2,则将它们分别定为α、β,然后在第二层个体中选择拥挤距离最大的个体作为δ;④若第一层灰狼个体数大于等于3,选择拥挤距离最大的3个个体分别作为α、β、δ。
原始灰狼算法中,在确定灰狼α、β、δ后,通过式(13)~式(15)对种群中其他灰狼的位置进行更新。考虑到上述集成问题存在正常生产和一种预防维护两种情形,需将上述编码分为两段,分别按照式(13)~式(15)对每段进行更新,实现灰狼ω位置的更新。
2.4 交叉算子与种群更新机制
原始灰狼算法中灰狼间没有信息交流。为了有效提升狼群的进化效率,提高算法的全局搜索能力,在算法中加入双点交叉算子。对于狼群中任意的灰狼个体,当交叉概率CR大于随机数时,从狼群中随机选取一只灰狼个体与当前灰狼个体进行交叉,具体交叉方法如图2所示。

每次迭代最后将本次迭代中通过位置更新和双点交叉产生的新个体与原种群中的个体进行结合,计算所有个体的目标函数值,并重新构建Pareto层级。依据每一只灰狼所处的层级和拥挤距离,从集合中选择出新的种群加入下一次迭代。选择的过程按照下列步骤进行:
步骤1对母代种群和子代种群进行Pareto分层。
高职院校相对比较封闭,创新创业项目的开展应该在开放的环境中进行。创新团队外出交流,不仅可以学习到新的理念、技术,更可以认识技术同行,为自身项目完善、发展提供更多机会。外出参加的活动主题可以与创新团队的研究目标有关,也可以与学生专业相关,既可以是创新创业类活动,又可以是创新创业专项训练。既可以走出去,又可以引进来。创客空间可以利用自身场,举办讲座、沙龙等活动。
步骤2创建新种群Ф,Pareto当前层数k=1。
步骤3若第k层个体数Nk+|Ф|小于设定种群规模PS时,将第k层所有个体加入新种群Ф中,转步骤4;反之,对当前层按照拥挤距离从大到小进行排序,选择(PS-|Ф|)个个体进入新种群,转步骤5。
步骤4k=k+1,转步骤3。
步骤5新种群Ф作为母代种群进行下一次迭代。
2.5 改进灰狼算法流程
按前文所述,改进后多目标灰狼算法流程伪代码如下,其中POS表示Pareto最优前沿,random_number表示随机数。
算法1改进多目标灰狼算法(IMOGWO)。
输入装配线平衡问题数据。
开始:
基于随机键的编码和解码,初始化狼群;
构建 POS;
For k=1 to t do
基于Pareto层级进行狼群等级划分,确认α、β、δ;
For m=1 to PS do
采用进化机制(式(13)~式(15))更新灰狼ωm;
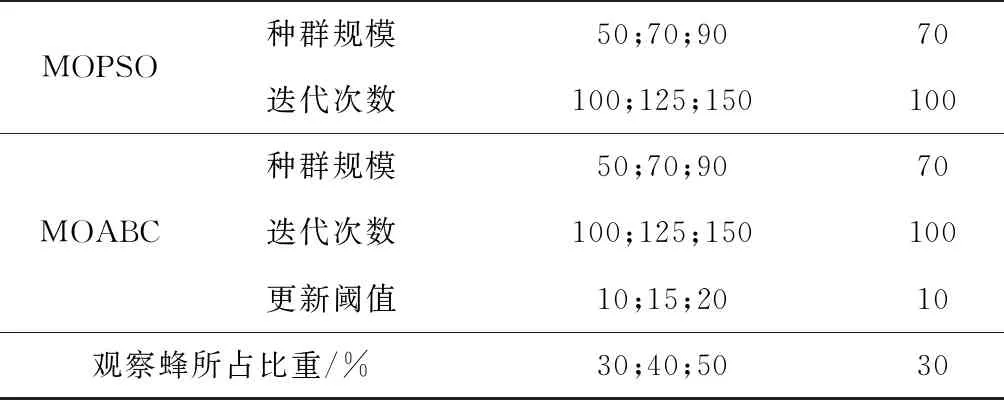
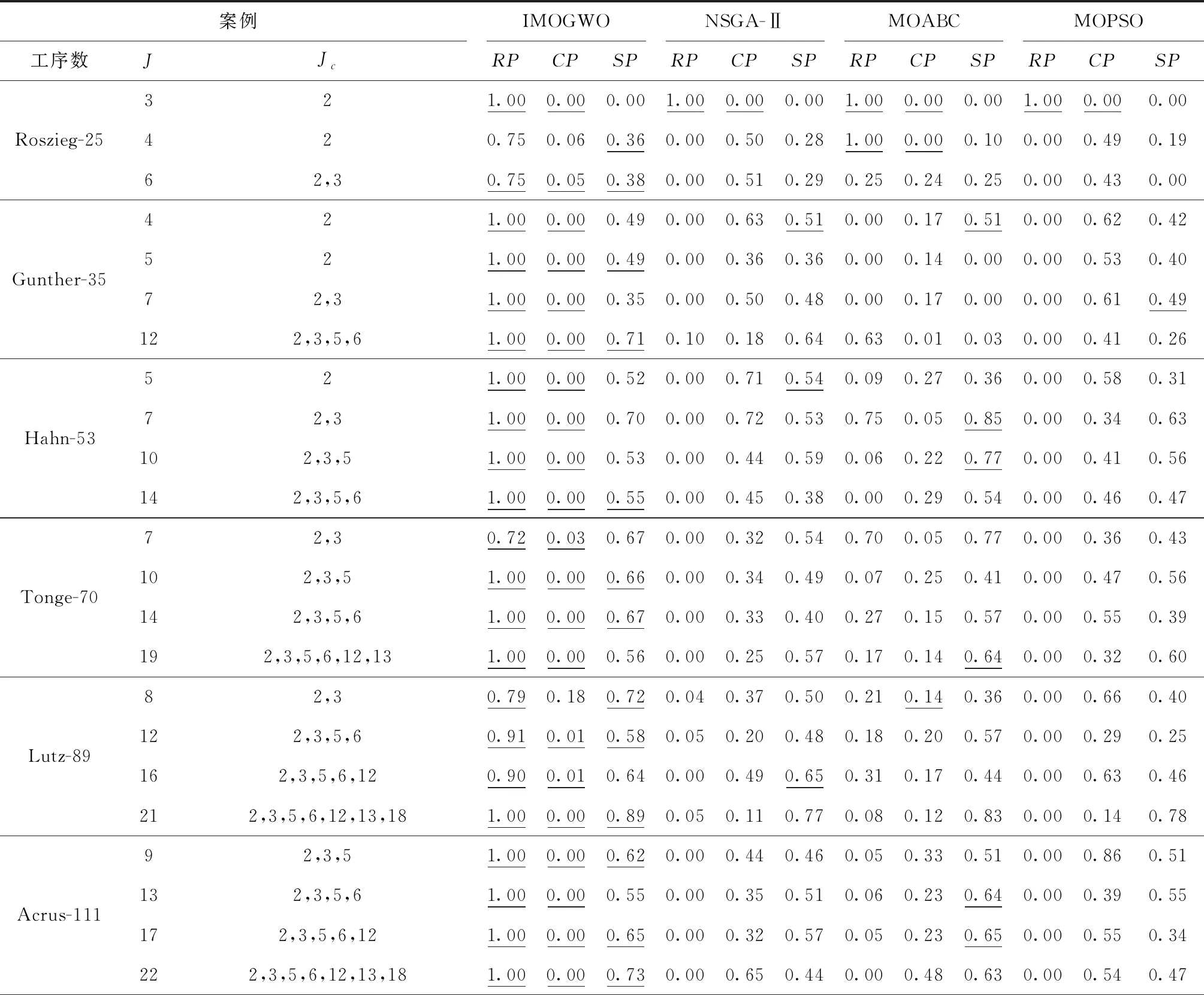
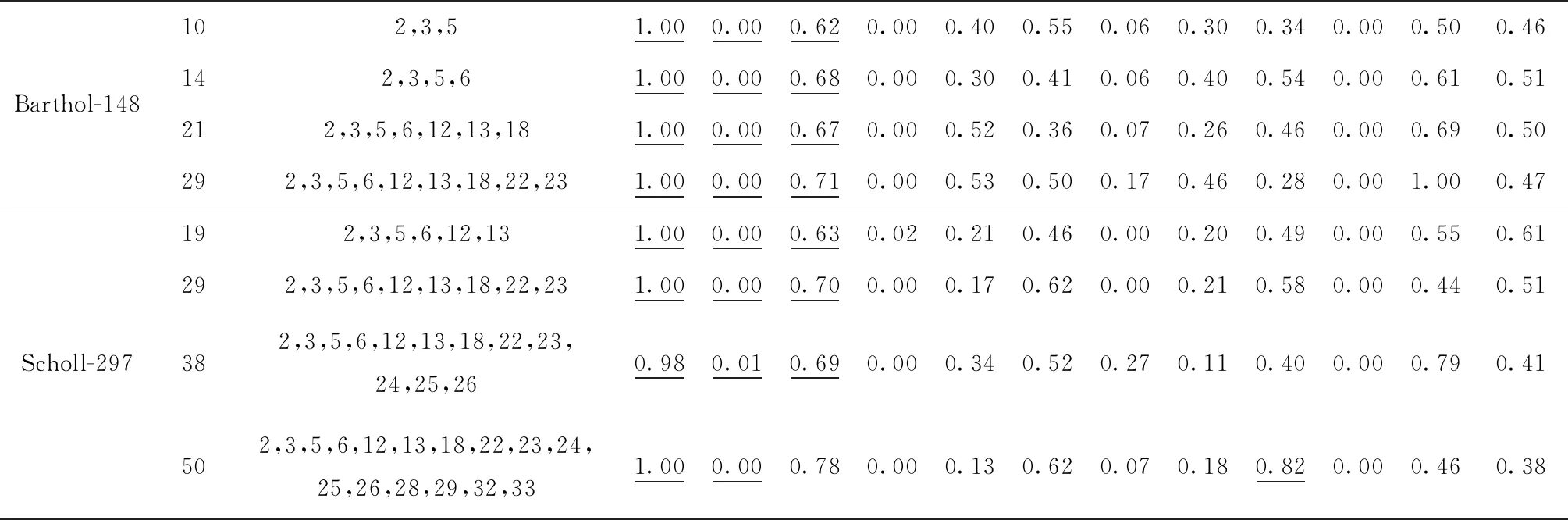
If random_number 对ωm进行双点交叉; End If End For 更新POS; 采用种群更新机制,形成新的灰狼种群; End for 输出POS 为验证算法性能,将改进后算法与带精英策略的快速非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm Ⅱ, NSGA-Ⅱ)[18]、多目标粒子群优化算法(Multi-Objective Particle Swarm Optimization algorithm, MOPSO)[19]、多目标人工蜂群算法(Multi-Objective Artificial Bee Colony algorithm, MOABC)[20]进行对比,为保证对比的公平性,对所有对比算法都进行重新编码和调整,并在相同配置电脑上运行,采用MATLAB 2016a进行编程,电脑配置为:Intel Core i5 CPU,2.40 GHz and 4.00 GB RAM。装配线实验数据来自装配线平衡专业网站https://assembly-line-balancing.de/;维护工位采用随机方式生成,每个案例随机指定一个或多个需要维护的工位。 图3所示分别展示了正常工作情形下与工位(2,3,5)同时预防维护情形下的最佳工序安排,所选案例为标杆案例中148工序-10工位的案例。 图3中方块上的数字代表工序序号,灰色方块表示需进行调整的工序,白色方块表示不需进行调整的工序。在图3a中10个工位均正常工作,最优生产节拍很小,为429分;但由于工位(2,3,5)3个工位需要同时进行维护,生产节拍变动很大,增长到620分,且生产调整数很大,需要调整110个工序,包含图3中灰色所示的{1,2,3,…,147,148}工序。 与未集成相比,将装配线平衡与预防维护集成后具有明显优势。以一天为例,假设每个工位每天工作8 h,工位维护需要4 h,工序调整时间需10 min。在不考虑集成时,只要设备预防维护则整线停工,导致总工作时间变成4 h,按照每小时产值200万计算,直接损失800万。在考虑集成时,设备维护与工序调整并行,待工序调整后继续工作。并在设备维护结束前10 min恢复正常工序分配。总工作时间为7.67 h。比未集成时增加192%。按调整工序后每小时产值140万计算,直接损失将降至287万,比未集成时减少517万。 为评价改进算法的性能,采用非支配解率RP、Pareto前沿解收敛性CP、个体间距离指标SP三个指标[21]评价解集的优劣性。 (1)非支配解率RP对于每一个Pareto解集Si(i=1,2,3…,s,S=S1+S2+…+Si+…+Ss),解集Si中不被其他解集支配的解所占的比重称为非支配解率,RP值越高,解集Si性能越好。 (17) 式中:y≻x表示y支配x;|Si|表示解集Si的数量。 (2)Pareto前沿解收敛性CP表示Pareto解集Si与近似true-Pareto解集TP的不同。 (18) (19) (3)个体间距度量指标SP衡量Pareto集合的分布性。 (20) (21) 算法对比前,使用Minitab软件中的田口实验对IMOGWO算法进行参数校验。首先通过田口实验产生9组参数值(如表2)。将每一组参数带入算法进行计算,得到当前参数对应的计算结果。然后将所有参数对应的结果合在一起,计算出总结果中的Pareto前沿,然后计算每组结果中Pareto前沿解所占比重,即非支配解率RP。最终得到结果如表2所示。对每组的RP值进行分析,得到信噪比主效应图(如图4)。 表2 IMOGWO参数校验 由图4可以得出IMOGWO的最佳参数组合为:种群大小90,交叉概率0.7,迭代次数100。为保证实验的公正性,考虑本问题特殊性对各对比算法做出如下改动。其中NSGA-Ⅱ采用相同编码解码方案,采用单点交叉、保留原始算法更新机制,交叉变异后分别计算适应度值并更新非支配解集;多目标粒子群算法(MOPSO)采用相同编码解码方案,保留原始算法更新机制;多目标人工蜂群算法(MOABC)采用相同编码解码方案,雇佣蜂、观察蜂、侦查蜂每个阶段结束时更新外部档案。对上述对比算法同样进行参数检验,得到各算法最优参数组合如表3所示。 表3 各算法参数组合 续表3 表4分别展示了4种算法在31个案例中的计算结果。每个算法下的3列数据分别对应当前算法在每个案例中计算出的3个指标值:RP、CP、SP。其中,加下划线表示性能较好的算法案例。 表4 多目标优化算法性能 续表4 分析表5可知,IMOGWO的RP值基本为1,表明该算法在每一个案例中得到的Pareto前沿解能支配NSGA-Ⅱ、MOABC、MOPSO等算法得到的Pareto前沿解集;此外IMOGWO计算得到的CP值均较小,说明该算法的收敛性优于其他3个算法;IMOGWO的SP值在20个案例中大于其他算法,说明IMOGWO在多数案例中具有较好的分布性。 综上表明,相对于NSGA-Ⅱ、MOABC、MOPSO算法,IMOGWO能高效地搜索到更多更优的解,对于解决装配线平衡与工位预防维护的集成问题具有明显的优势。进一步分析主要得益于算法在几个方面的改进:①相比于对比算法,灰狼算法通过让3只适应度值最优的头狼引导种群进化,加快了种群的进化速度,促成了灰狼算法所得的前沿解对其他算法前沿解的支配性;②引入遗传算法中的交叉算子,提高了种群内部的交流,让算法在每个案例中皆具有较好的分布性;③独特的种群更新机制,即将新生成个体与原种群个体合在一起计算适应度值,选择其中优秀的个体进入下一代,充分保留了种群中的优秀基因,防止算法在迭代过程中丢失种群更新的方向。 针对目前装配线上不论设备预防维护或故障维护,都必须生产中断,带来巨大生产损失的问题,提出将装配线平衡与工位预防维护两个独立子系统进行集成,同时制定多套、能容留设备维护契机的装配生产计划,通过多套计划之间的快速切换,保证生产时的设备可维护性和维护时的生产连续性。针对该集成问题,构建数学规划模型,指明不仅应达成各工位在正常工作和工位维护情形下的节拍最小化,以保证生产效率,还应对正常工作与预防维护情形之间切换时的工序调整最小化,以稳定生产。设计基于随机键的编码和解码方法,并提出融合Pareto层级构造和拥挤距离的多目标进化机制,研制IMOGWO算法进行求解。实验表明,所提出的IMOGWO算法在非支配率、收敛性和分布性指标上,优于其他算法,同时证明了采用集成方法后装配生产损失大幅减小,生产连续性显著提升。未来的研究将考虑一些更加复杂的生产情形,如多种产品在同一条装配线上进行加工等。3 实验分析与讨论
3.1 案例描述

3.2 多目标Pareto前沿评价指标与参数校验
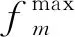


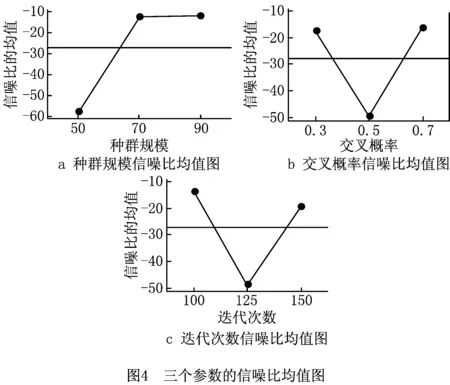
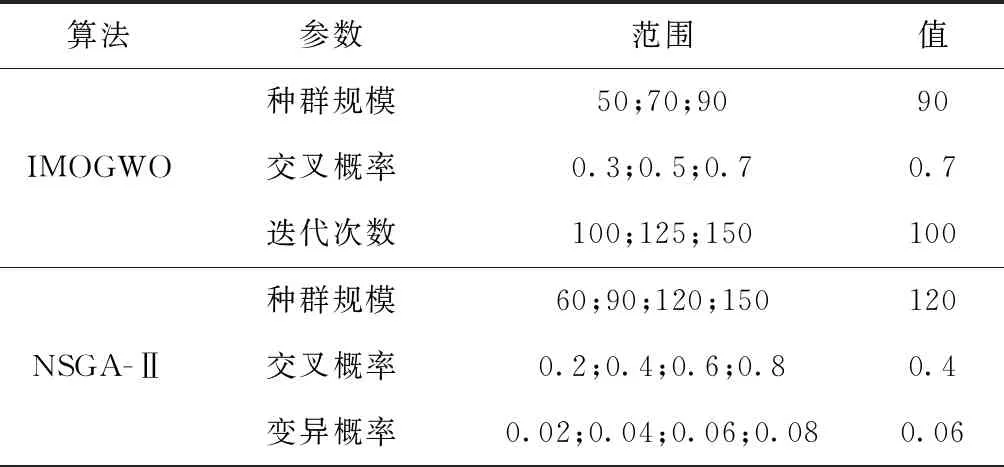
3.3 算法性能分析
4 结束语
