风力发电机组铸造主轴胀套联接应力测量与分析
2021-01-14何先照应华冬
裘 园,何先照,应华冬
(1. 浙江运达风电股份有限公司,杭州310012;2. 浙江省风力发电技术重点实验室,杭州310012)
铸造工艺具备成品率高,质量稳定,便于批量生产的特点,因此风力发电机组主轴广泛开始采用铸造工艺进行生产。而风力发电机组主轴与齿轮箱的联接,主要采用胀紧套联接的形式,该联接方式具备构造简单,传扭能力高,抗冲击载荷等的优点[1]。为了能够将主轴的扭矩传递给齿轮箱,胀紧套对主轴必须要有足够的抱紧力。陕西科技大学的张锋等介绍了运用拉梅方程来设计胀紧套的理论算法[2],重庆大学的杜静等使用有限元软件分析了不同的间隙和摩擦系数对胀紧套接触应力的影响[3],何章涛等对拉梅方程理论计算和有限元分析结果做了对比[4]。为了将理论计算和有限元分析结果与实际应力进行比较,对某大MW 风电机组的胀紧套进行应力测量试验,在主轴钢套内侧贴应变片,通过测量胀紧套安装前后刚套内表面的应变值,从而获得刚套内表面的应力变化,将拉梅方程的理论计算结果和有限元仿真结果进行对比,从而为主轴和胀紧套的设计优化提供参考。
1 胀紧套工作原理
风力发电机组主轴、 胀紧套与齿轮箱的装配关系如图1 所示,主轴将风轮叶片产生的扭矩通过胀紧套传递到齿轮箱,经过齿轮箱增速后传递给发电机。胀紧套参照标准《JB/T 7934-1999 胀紧联结套型式与基本尺寸》设计,其结构详见图1,通过拧紧收缩盘内外环之间的螺栓,产生轴向拉伸力,经过内外环锥面转变为径向的抱紧力,使行星架抱紧主轴,从而产生足够的静摩擦力,将主轴的扭矩传递到齿轮箱。同时在收缩盘内外环设计了一个止口,通过止口来限制收缩盘内外环的相对位移,从而既保证胀紧套有足够的扭矩传递能力,又不至于使各部件的应力超过许用应力。
2 理论计算
如图1 所示,拧紧收缩盘内外环之间的螺栓后,收缩盘外环沿斜面滑移后,胀紧套各个接触面之间将产生变形和接触压力。根据变形协调条件计算出各个接触面之间的接触压强后,将各部件等效为厚壁圆筒模型,运用拉梅方程算出各个部件内外表面的应力。
假设钢套外径位移为δ,主轴外径位移量为△1,主轴内径位移量为△2,行星架外径位移量为△3,行星架内径位移量为△4,收缩盘内环内径位移量为△5。经过测量,主轴内径与钢套外径之间的间隙△d2=-0.04 mm,主轴外径与行星架内径之间的间隙△d1=0.052 mm,行星架外径与收缩盘内径之间的间隙△d0= 0.0885 mm。胀紧套各部件的材料性能如表1所示。
根据变形协调条件,接触面位移差等于各接触面之间的间隙,可得:

收缩盘内环内径位移量:
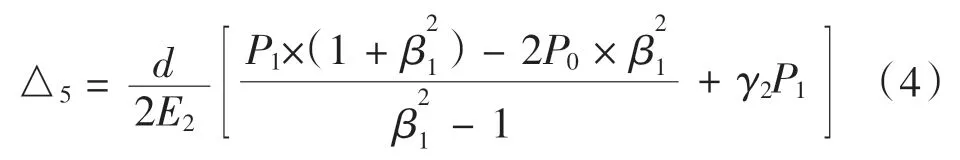
其中,P0为收缩盘内外环之间的接触压强,P1为收缩盘内环与行星架之间的接触压强,β1= dave/d。
行星架外径的位移量:
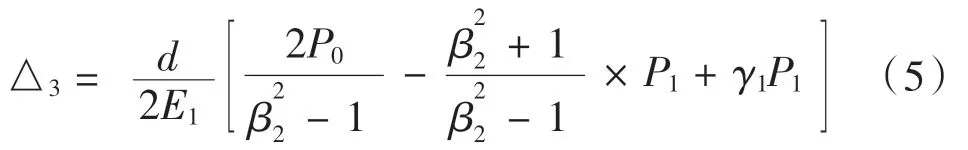
行星架内径的位移量:
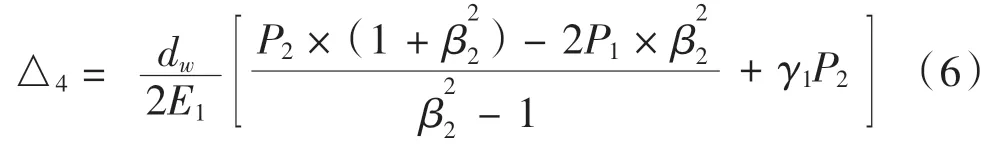
其中P2为行星架与主轴之间的接触压强,β2=d/dw。
主轴外径的位移量:

主轴内径的位移量:

其中,P3为主轴与钢套之间的接触压强,β3=dw/di。
钢套外径的位移量:
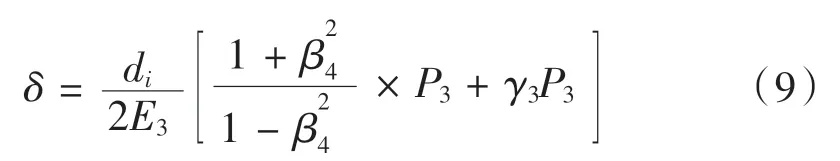
其中,β4= di/dg。
收缩盘内外环之间的接触压强P0为:
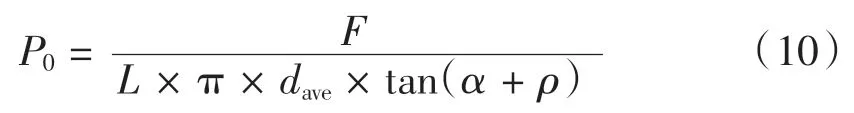
其中F 为胀紧套螺栓的预紧力,收缩盘的长度L=370 mm,dave= 993.3 mm,收缩盘斜面角 α = 2.7°,摩擦角 ρ = arctan0.045 = 2.58°。
已知应力测量试验时,采用液压拉伸器分四次按照十字交叉法拧紧螺栓,每次拧紧时增加1/4 的螺栓额定预紧力(具体见第4 部分)。试验中会分别记录第二次和最后一次螺栓拧紧时液压拉伸器的压力和应变片的数据。为方便表述,将第二次螺栓拧紧时的工况称为工况一,将最后一次螺栓完全拧紧后达到额定预紧力的工况称为为工况二。根据记录的液压值计算得到的胀紧套螺栓预紧力分别为9 742.7 kN、 19567.1 kN。胀紧套各部件的材料性能如表1 所示,将螺栓预紧力代入,联立公式(1)-(9),可得各表面的接触压强,如表2 所示。

表2 各工况下的接触压强
将胀紧套各部件等效为厚壁圆筒模型,运用拉梅方程来计算各部件内外表面的应力。以行星架为例分析其外径处的应力,行星架内外径分别受到P1、P2的挤压应力,则:
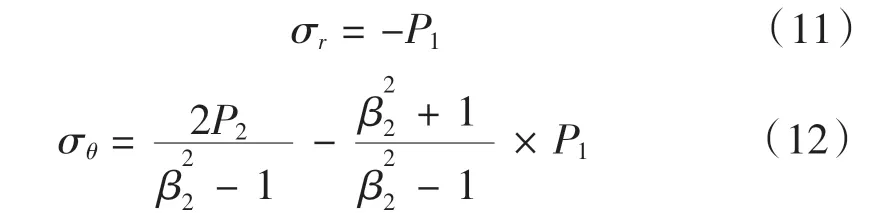
按照第四强度理论,等效应力为:

同理可得,各部件内外径处的应力如表3 所示。
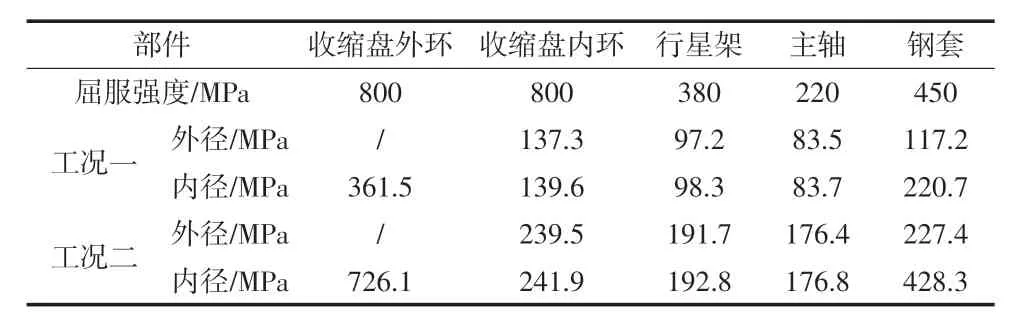
表3 各部件内外径的应力值
由于主轴热套时的高温会使刚套内表面应变片的胶水失效,导致应变片无法测得试验数据,因此需在热套后待主轴与刚套完全冷却至室温,才在刚套内表面贴应变片,所以应变片测量的是刚套安装后直至整个胀紧套安装完成,螺栓按额定扭矩拧紧时的应力变化。因此还需要计算主轴热套钢套后,钢套内径处的应力值。计算方法与前面一致,不再详述,代入主轴内径与钢套外径之间的间隙△d2= -0.04 mm,计算可得钢套内径处的应力为24.5 MPa。则在工况一和工况二时,钢套内径处的应力变量分别为196.2 MPa 和 403.8 MPa。
3 有限元仿真
按照前面理论计算的模型绘制三维模型,简化了胀紧套收缩盘内外环之间的螺栓,模型如图2 所示。各个接触面的设置如表4 所示。将主轴大法兰端面和行星架端面固定,限制收缩盘内环的轴向位移,在收缩盘外环端面增加一个载荷伞,在loadpoint 分别施加胀紧套M33 螺栓的预紧力,有限元仿真的结果如图3、图4 所示。为了与试验结果作比较,测量钢套内经贴应变片处的应力,结果如表5 所示。

图2 有限元仿真模型
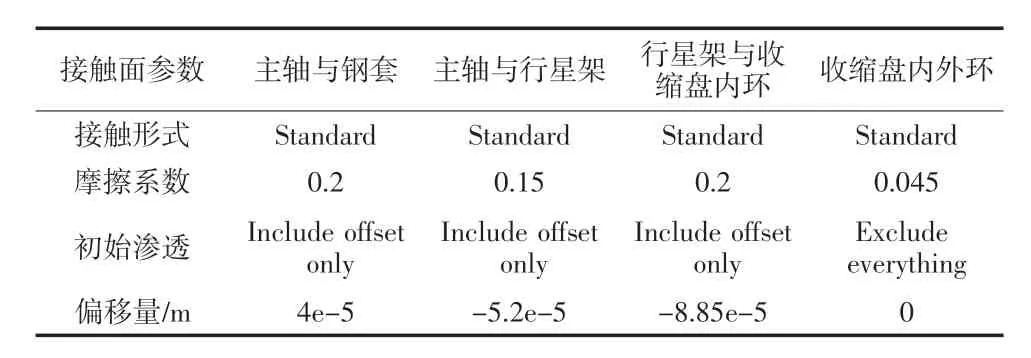
表4 接触面参数设置

图3 工况一时主轴钢套的应力图
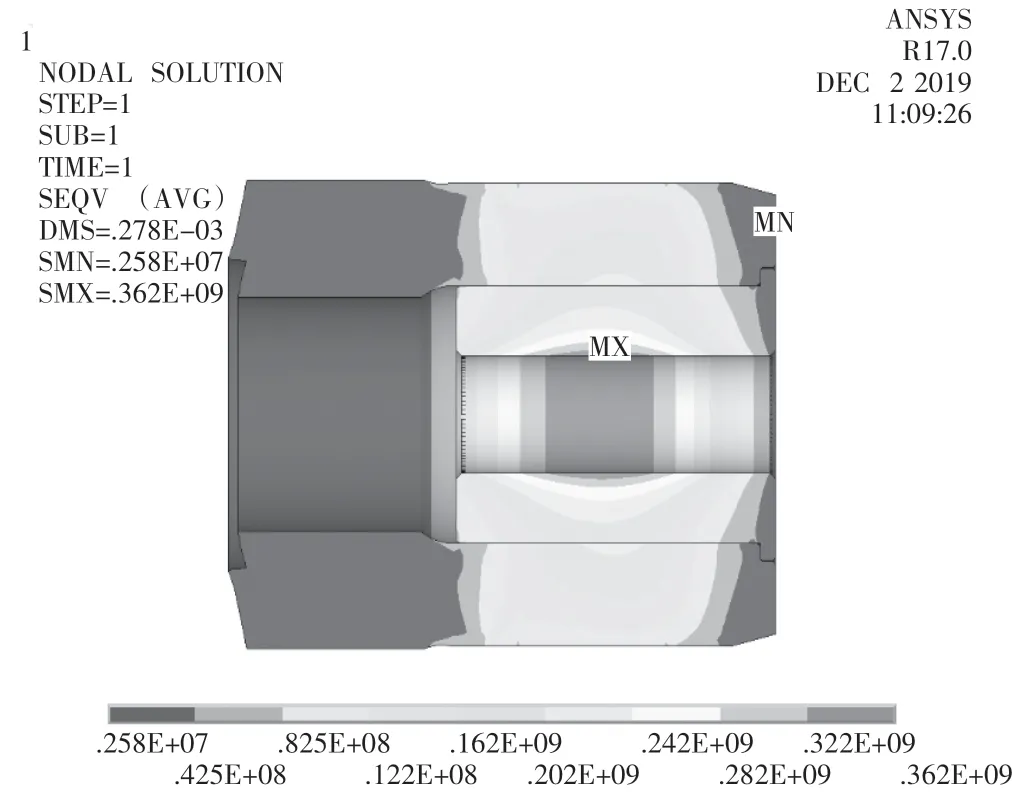
图4 工况二时主轴钢套的应力图

表5 钢套内侧应力最大值及应变片出的应力
有限元仿真的结果是胀紧套、主轴、钢套共同作用的结果,为了与试验结果对比,还要减去钢套热套后钢套内径处的应力。建立主轴和钢套的有限元模型,主轴大法兰端固定,主轴与钢套之间建立Standard 接触,摩擦系数0.2,初始渗透Include offset only,偏移量4e-5m,结果如图5 所示,测得贴应变片处的应力值为23.5 MPa。则工况一时,钢套内径贴应变片处的应力增量为159.1 MPa;工况二时,钢套内径贴应变片处的应力增量为276.4 MPa。

图5 热套后主轴刚套的应力图
4 应力测量试验
为了获得真实的应力结果,胀紧套安装前,在钢套内径处贴了4 组应变片,位置如图1 所示,在距离主轴小端面200 mm 处,沿内壁周向均匀分布,应变片安装完后如图6 所示。应变片安装完成后,记录应变片的应变初始值。在胀紧套安装到主轴上后,先按照额定扭矩的一半拉伸螺栓,记录应变片的应变值;再按额定预紧力拉伸螺栓,记录应变片的应变值。应变片的测量结果如表6 所示。已知钢套的材料为34CrNiMo6,弹性模量 E = 2.1 × 105 MPa,则工况一时,4 组应变片的平均应变量为1 145.103 μm/m,应力增量为240.5 MPa;工况二时,4 组应变片的平均应变量为1 262.427 μm/m,应力增量为265.1 MPa。

图6 应变片安装示意图
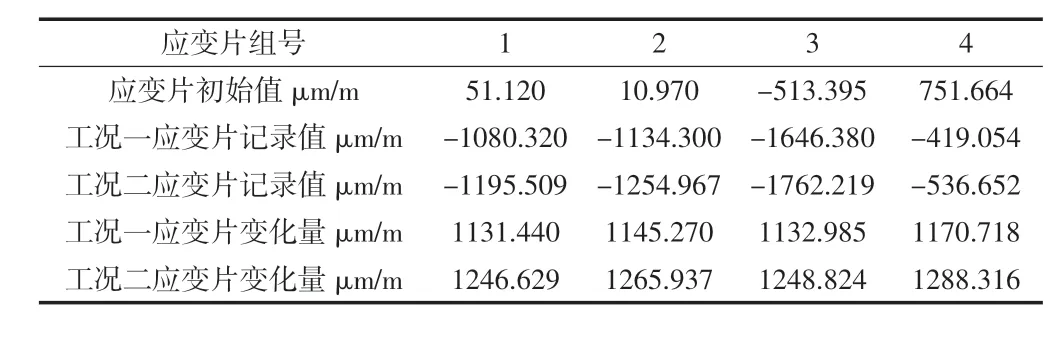
表6 应变片数据记录表
5 结果对比
应力测量得到的结果与理论计算、 有限元仿真对比如表7 所示。工况一时,无论是理论计算还是有限元仿真,与试验得到的结果都相差较大。工况二时,理论计算的应力值要比实际测得的应力值大52.3%,而有限元仿真的结果与试验测得结果非常接近,当按照额定扭矩拧紧螺栓之后,两者的偏差只有4.3%。经过分析,收缩盘内外环之间的摩擦系数0.045 远大于实际的摩擦系数,经过与胀紧套厂家的交流,实际摩擦系数约为0.01。将收缩盘内外环之间的摩擦系数设置为0.01,则根据拉梅方程理论计算后可得刚套内侧的应力为347.4 MPa,除去刚套热套后的应力增量24.5 MPa,实际应力增量为322.9 MPa。更改有限元模型中收缩盘内外环之间的摩擦系数为0.01,则有限元仿真结果如图7 所示,应变片处的应力为268.2 MPa,除去刚套热套后的应力增量23.5 MPa,则实际应力增量为244.7 MPa。工况二时,理论计算得到的刚套内侧应力增量为658.1 MPa,有限元仿真刚套内侧应变片处的应力增量为275.8 MPa,如图8 所示。修改摩擦系数为0.01 后应力测量得到的结果与理论计算、 有限元仿真对比如表8 所示,从表中可以看出,此时理论计算的结果与试验结果依然相差甚远,两个工况的偏差分别达到了34.2%和148.2%;有限元仿真的结果与试验测得结果非常接近,两个工况的偏差分别为1.7%和4.0%。从理论计算、有限元仿真与试验结果的对比来看,主要有以下结论:首先收缩盘内外环之间的实际摩擦系数远小于0.045;其次,运用拉梅方程理论计算的过程中,做了很多的简化,例如未考虑各接触面的边缘效应,未考虑止口的作用等,导致理论计算结果与实际偏差很大,而有限元仿真能够更真实的模拟胀紧套安装的实际情况,获得的结果也与实际相符。实际中更应优先采用有限元方法指导其安装优化。
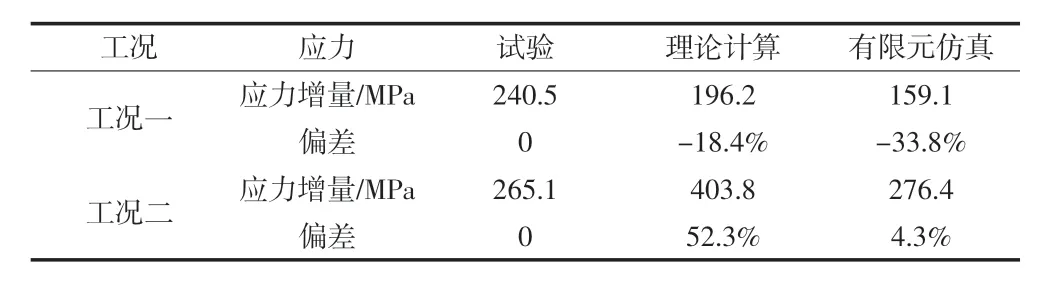
表7 应力测量结果与拉梅方程、有限元仿真结果对比

图7 工况一收缩盘内外环摩擦系数为0.01 时主轴刚套的应力图

图8 工况二收缩盘内外环摩擦系数为0.01 时主轴刚套的应力图

表8 收缩盘内外环摩擦系数为0.01 时应力测量结果与拉梅方程、有限元仿真结果对比
6 结束语
本文分别通过拉梅方程、有限元仿真,对风力发电机组铸造主轴尾端与齿轮箱胀紧套联接部分的强度进行分析,并与试验测得的结果进行对比,有限元仿真能够更好地模拟主轴和胀紧套的实际应力,实际中更应优先采用有限元方法为主轴和胀紧套强度校核。
