基于双频加权组合的土壤含水量估算方法研究
2021-01-14王浩宇张志刚梁月吉时梦琪
王浩宇,张志刚,梁月吉,任 超,时梦琪
(1.桂林理工大学测绘地理信息学院,广西 桂林 541004;2.广西空间信息与测绘重点实验室,广西 桂林 541004)
0 引 言
目前,国内外利用GPS-IR遥感技术监测土壤湿度的研究很多。1993年,Martin-Neria[1]第1次用GNSS-R信号进行海面测高的技术,发现反射信号对土壤湿度十分敏感,地表反射GPS信号功率是土壤介电常数的函数。Bilich等[2]发现反射信号分离后,信噪比的幅频特性与多径环境有很强的相关性,研究了信噪比(Signal-to-Noise Ratio,SNR)观测中直接分量和反射分量的分离以及反射分量与反射环境的关系,并对相位观测进行了修正。Larson等通过研究信噪比数据和气象数据,验证了多径干扰幅度与降水事件之间存在强相关性[3-4]。Chew等利用大陆板块边界观测网络SNR观测数据和相关场地的测量土壤水分数据已得到更多验证:干扰相位,幅度和频率计算有效高度与土壤湿度之间存在很强的相关性[5-6]。敖敏思等利用指数函数能较好地描述SNR多径延迟相位与土壤湿度之间的关系[7]。汉牟田等利用振荡振幅反演土壤湿度时得出一个结论,反演结果的准确性在不同高度和介电常数的反射系数的敏感性估计误差,敏感性弱的仰角更适合反演[8]。丰秋林等利用BP神经网络模反演土壤湿度,表明该方法明显优于线性回归统计的方法反演土壤湿度,证明了该方法的可靠性[9]。梁月吉等通过最小二乘支持向量机和神经网络实现了多颗GPS卫星的初步融合,验证了基于多星融合的土壤湿度反演精度相对于单颗卫星有了较为明显的提高[10-11]。然而,这些算法难以实现多载波的互补和融合,通过建立物理或数学模型对L1和L2载波进行融合将更有利于土壤湿度的反演。因此,本文围绕多载波组合反演问题,基于多元线性回归原理,研究和建立了土壤湿度单星线性回归反演模型;并通过美国板块边界观测计划(Plate Boundary Observatory,PBO)提供的监测数据,对利用单颗、多颗卫星反演土壤湿度的可行性和有效性进行了对比分析。
1 GPS-IR土壤湿度反演原理
1.1 GPS-IR反射信号原理
GPS-IR是一种由土壤反射的GNSS信号与直射信号的干涉效应实现土壤湿度反演的遥感技术[4]。信噪比SNR指的是接收卫星信号的强弱,GNSS接收机在接收卫星信号的过程中,受到接收机以外的地物或建筑物的影响,接收机同时接收卫星的直射信号和其他不同反射体的信号,两种信号相互干涉,产生多路径误差[5]。可以用直射信号和反射信号表示信噪比SNR,即
(1)
式中,Ad为直射信号;Am为反射信号;θ为卫星信号入射高度角;ψ为直射信号和反射信号的相位差。SNR观测数据如图1a所示。

图1 SNR及地面多路径误差几何模型
图1代表P041测站2011年第240 d PRN08号卫星的SNR干涉图和多路径误差几何模型。可见,在低卫星高度角下,GPS信噪比受多路径影响较为突出(如图1a中的虚线方框区域)。文献[10]表明,不同的卫星信号受多路径影响的程度均不一样,土壤湿度信息主要包含在多路径环境影响的成分中。图1b,θ为卫星信号入射高度角;h为天线距离底面的垂直高度;ε为坡面的倾斜角度;β为卫星信号与坡面间的夹角。当ε较小时,可表示为
θ=β+ε≈β
(2)
文献[5]的研究表明:SNR观测值与ψ之间存在一种正弦或余弦关系,而且GPS土壤湿度仅与多路径反射信号相关,那么去除GPS卫星直射信号后的多路径反射信号与sinθ之间仍存在某一固定频率的正弦(或余弦)函数关系。即
(3)
式中,θ为卫星入射高度角;λ为载波波长;h为GPS天线高;AMR2为多路径反射信号的振幅,φMR2为相对延迟相位。AMR2和φMR2即为需求的特征参数。
1.2 GA-BP神经网络
遗传算法是一种模拟自然界生物进化和遗传机制且具有自适应、自学习等优点的全局优化概率搜索算法[12]。BP神经网络是一种基于误差反向传播算法的多层前馈神经网络。网络的训练过程由信号的正向传播和误差的反向传播两个过程组成[13]。
反射信号的干涉相位等特征参数与土壤水分呈线性关系,所以将L2C信号的SNR观测值反射信号分量的振幅Am和相位ψ作为输入项,构建输入变量Xi=[Am,ψ],而期望输出值Y则是实际土壤湿度。将数据导入输入层之后,要先对数据做归一化处理,使数据明显呈梯度变化趋势,收敛速度加快,归一化计算公式为
X=2(Xi-Xmin)/(Xmax-Xmin)-1
(4)
式中,X为归一化后的值;Xi为变量中的某一个值;Xmin为变量中最小的值;Xmax为变量中最大的值。
隐藏层的处理和变换主要是通过隐藏层与输入层之间的权值ω和阈值b以及激活函数来实现,隐藏层的输入值和输出值分别为
(5)

(6)

(7)
式中,m为隐藏层神经元个数;n和q分别为输入和输出个数;a为0~10的整数。利用matlab编程实现双频加权组合模型的建立。
2 实验结果与分析
2.1 数据来源
本文使用的是美国板块边界观测计划PBO中P041测站2011年第240天到272天的L1和L2 载波SNR数据。该测站位于西经105.194267度、北纬39.949493度,很早就开展土壤湿度分析,具有一定的代表性;其周边地形较为平坦、开阔且植被稀少,有利于土壤湿度监测。站点均采用钢制三角支架安置,接收机型号为TRIMBLE NERT9,采用SCIT的天线罩,天线型号为TRM59800.80。P041测站2011年第240天~第272天 (共33 d)的土壤湿度(Soil Moisture Content,SMC)参考值也是由美国板块边界观测计划PBO提供。
2.2 实验分析
利用TEQC和最小二乘拟合得到SNR1和SNR2对应的相位值,选择一个时间段的相位数据,筛选有SNR1和SNR2对应的多径延迟相位值数据,分别求得L1频点和L2频点相位与土壤湿度的相关性,限于篇幅,仅给出部分卫星的L1频点和L2频点多径延迟相位与土壤湿度的线性相关性(见图2)。

图2 各卫星L1和L2多径延迟相位与土壤湿度的相关性
由图2可见,各卫星的多径延迟相位与土壤湿度的线性相关系数R2均不一致,这可能是由于各卫星的方位角以及性能差异造成。进一步对比各卫星发现,不同卫星对于土壤湿度变化的响应模式并不一致。因此,在未知土壤湿度的条件下,通过某种方法剔除异常卫星反演结果比较困难,也不利于土壤湿度的连续监测。通过对多频点反演结果融合形成互补,经GA-BP神经网络估算土壤湿度成为可能。本文为了进一步评估双频融合的性能,设置3种方案进行实验对比分析:方案1基于L1频点的多径延迟相位进行GA-BP神经网络回归分析;方案2基于L2频点的多径延迟相位进行GA-BP神经网络回归分析;方案3基于双频融合的多径延迟相位进行GA-BP神经网络回归分析;将L1和L2的多径延迟相位分别建立GA-BP神经网络处理,包括训练样本(Training)、验证样本(Validation)、测试样本(test)、总体的预测结果(all)(见图3)。
由图3和图4可见,图3a、3b分别为PRN11、PRN17两颗卫星在L1单频回归分析图;图3c、3d分别为PRN11、PRN17两颗卫星在L2单频回归分析图。L1单频回归系数R值都在0.9以上,L2单频回归系数R值都在0.7以上;卫星在两个频点建立的GA-BP模型后估算精度都得到了有效改善。由图3e、3f可见,PRN11、PRN17两颗卫星双频融合的回归系数R值都在0.9以上,估算误差稳定,预测精度较高,充分发挥了模型的优势,对L1和L2频点形成了有效互补。图4是融合前L1频点、L2频点和融合后反演结果。其中,PRN11融合后R2为0.865,比L1频点和L2频点提高60%;PRN17融合后R2为0.824,比L1频点提高83.1%,比L2频点提高38.5%。为了进一步评定各方案的精度,本文利用相关系数R2,平均绝对误差(MAE)和均方根误差(RMSE)进行精度评定,如表1所示。PRN11融合后的R2为0.865,相对于L1和L2频点提高60.8%;RMSE为0.037,相比L1频点降低了90%以上,相比L2频点提高19.4%;MAE为0.034,相比L1频点降低90%以上,相比L2频点提高61.9%。PRN17融合后的R2为0.824,相对于L1和L2频点分别提高83.1%和38.5%;PRN17融合后RMSE为0.045,比L1频点降低90%以上,相比L2频点提高45.1%;MAE为0.042,比L1频点降低90%以上,相比L2频点提高90%以上。综上所述,采用GA-BP神经网络双频回归分析的相关系数均优于单频反演结果,RMSE、MAE精度相比L1得到明显降低。双频相比单频可靠性高,能够有效反映土壤湿度的变化规律。
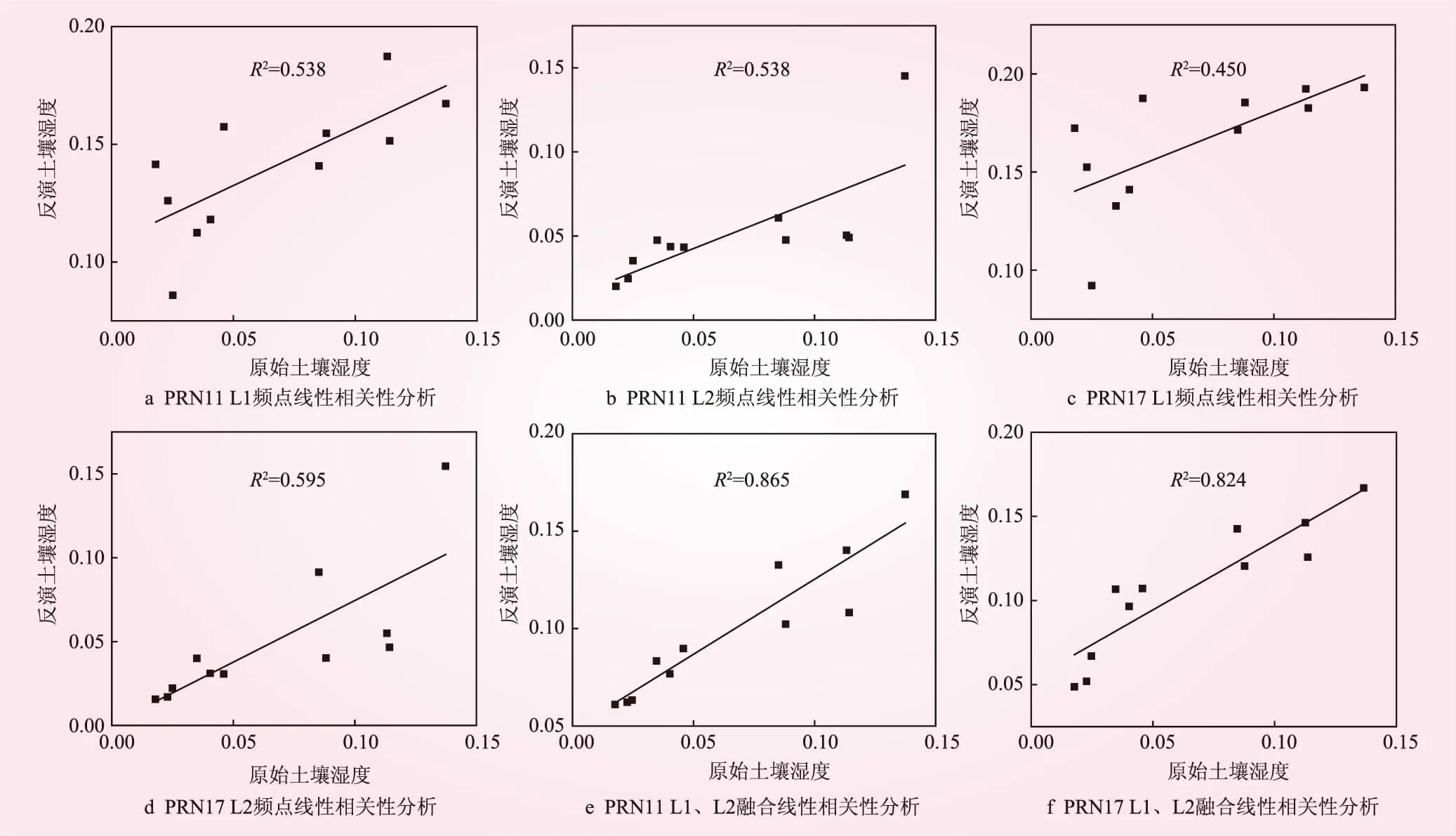
图4 各方案反演土壤湿度与原始土壤湿度的相关性

表1 各模型反演土壤湿度估算精度统计
3 结 论
本文提出了一种基于GPS-IR双频加权融合的土壤湿度反演方法。通过采用遗传BP神经网络方法和多元线性回归分析,对两个频点SNR相位观测量进行融合处理。理论分析和各实验对比结果表明:
(1)采用GPS-IR技术能够有效实现测站周围土壤湿度的准确反演,大大改善了传统土壤湿度测量方法的时空分辨率。
(2)已有的研究较少考虑到双频多星组合估算土壤湿度的优势,利用单频不能把区域内所含的土壤信息完全表达,不利于估算精度的提高。因此,遗传BP神经网络双频多星融合反演土壤湿度,充分融合了各卫星两频点的优秀性能,能将各卫星两频点中质量好的数据得以保留,从而使反演结果得到提高。融合后的反演结果比单一频点的反演结果有显著提高。
(3)建立多元线性回归分析双频融合反演土壤湿度,可以根据L1、L2频点观测相位与实测土壤湿度之间的相关程度和回归拟合程度的高低,提高反演结果的准确性和预测方程式的效果。
