基于小波去噪与BP神经网络的地铁沉降组合预测方法

2021-01-14秦拥军张佳琪谭顺利

水力发电 2020年10期

秦拥军，张佳琪，谭顺利

(新疆大学建筑工程学院，新疆乌鲁木齐 830047)

0 引言

随着城市人口的不断增长和城市规模的不断扩大，我国城市地下工程发展迅速。然而，地下工程的施工不可避免的使地表产生变形，当地表变形超过安全限度时，就会影响到地下工程的安全运营和周边建筑物的正常使用，严重时还会造成人员伤亡。因此，精准预测地下工程施工引起的地表变形，对于防灾减灾具有重要的意义[1-5]。受测量仪器、人为操作、观测条件等因素的影响，监测数据不可避免的含有噪声污染。如何采用有效手段消除噪声，是提高预测模型精度的关键[6-8]。目前，对地下工程施工诱发的地表变形预测主要借助经验公式法[9-11]、数值模拟法[12-13]、解析法[14]以及人工神经网络预测法[15-19]。其中，人工神经网络以其简单易行、计算量小、并行性强等优势受到广泛应用。为了提高预测精度，大量学者采用小波去噪和神经网络组合预测。杨奇妹等[20]将小波分析与RBF神经网络相结合，建立了深基坑沉降预测模型，经实例验证预测误差保持在1%～5%，满足沉降监测要求；严容[21]将小波去噪和BP神经网络用于变形预测，取得了良好效果。

本文将小波去噪与神经网络应用于乌鲁木齐地铁沉降预测过程，依托乌鲁木齐市轨道交通1号线新疆大学站监测数据，采用小波理论对其进行降噪处理，并选用常用的BP神经网络进行沉降预测，取得了良好的效果。

1 工程概况

乌鲁木齐市轨道交通1号线新疆大学站共布置了125个监测点，编号为DB-01-06～DB-29-04、JCJ-01-10～JCJ-09-16、GCY-01-02～GCY-02-10及GCJ-01-02～GCJ-01-10。该站采用明挖法施工，车站类型为双柱三跨双层箱型框架结构，DB系列监测点及GCJ系列监测点均布设在基坑车站周围。其中，GCJ-01-07监测点不仅布置在基坑周围，且与已建建筑乌鲁木齐第二十小学教学楼相邻。监测点GCJ-01-07位置见图1。本文选取GCJ-01-07监测点在2016年5月19日～2016年8月15日之间的累计沉降量进行研究。原始数据回归分析见图2。由于原始数据本身存在的误差，使得沉降曲线出现局部波动的状况，这与实际变形趋势不符。因此，本文在进行沉降预测前，先对原始数据进行了降噪处理，从而减小了误差。

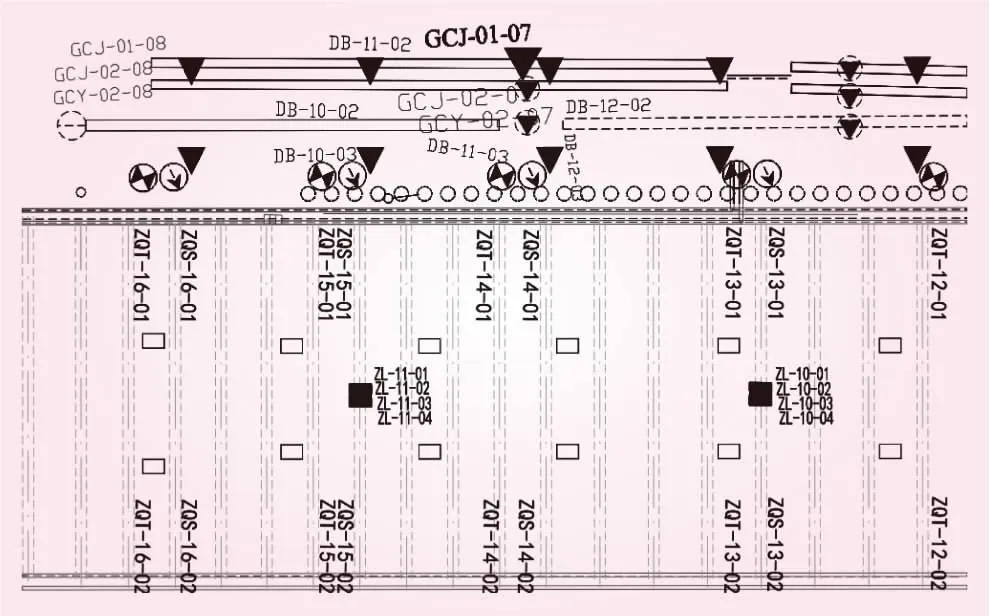
图1 监测点GCJ-01-07位置

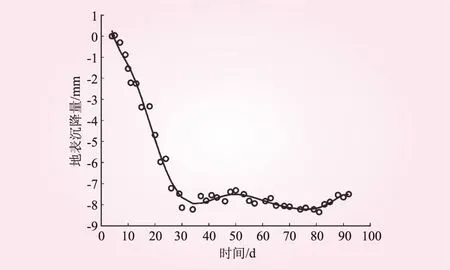
图2 原始数据回归分析

2 监测数据降噪

小波分析是近年来迅速发展的信号处理技术，能对多分辨率进行时频分析，被誉为数学显微镜[22-23]。由于监测数据中真实信号和噪声的时频特性不同，通过小波分析可对其进行有效分离，从而减小误差，获得真实的变形信息[24]。一般情况下，小波去噪的步骤为[25-30]：①根据工程的实际特点选择去噪参数；②阈值处理；③通过小波变换重构信号。

本文在对原始数据进行去噪之前，首先研究了各种去噪参数对去噪效果的影响，从而获得最优的去噪模型，以期达到最佳去噪效果。衡量小波去噪效果的指标主要有均方根误差(RMSE)和信噪比(SNR)。RMSE指降噪信号与原始信号的均方误差，RMSE越小则去噪效果越好。SNR指原始信号与噪声的能量比值，SNR越大则去噪效果越好。

2.1 不同阈值对去噪效果的影响

在小波去噪的过程中，阈值的选取方法主要有硬阈值和软阈值，选取标准主要有固定阈值(sqtwolog)、极大极小阈值(minimaxi)、无偏风险估计阈值(rigrsure)和启发式阈值(heursure)。基于相关文献的研究，采用工程中广泛使用的小波函数dbN和symN进行3层分解，以无偏风险估计阈值rigrsure为选取标准，scal=sln，分别用上述阈值对监测数据进行去噪处理，用SNR和RMSE衡量去噪效果。去噪结果见图3。图3中，①代表db小波系SNR；②代表db小波系RMSE；③代表sym小波系SNR；④代表sym小波系RMSE。从图3可知，无论在db小波系和sym小波系中选取何种阈值去噪，RMSE均相差不大，但硬阈值去噪的SNR明显大于软阈值，且rigrsure的SNR最高，说明硬阈值、rigrsure标准的去噪效果最好。

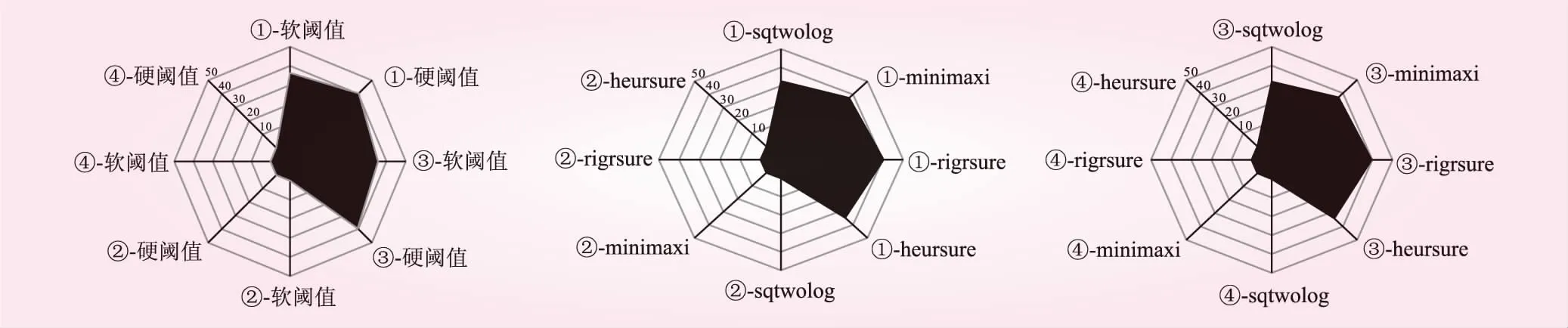
图3 不同阈值的去噪效果对比

2.2 不同scal对去噪效果的影响

scal表示阈值随噪声的变化，有scal=one、scal=sln、scal=mln等3种情况。采用前述方法对比其去噪效果。不同scal的去噪效果对比见表1。从表1可知，scal=sln的SNR明显高于其他两者，且RMSE最小，说明scal=sln时的去噪效果最好。

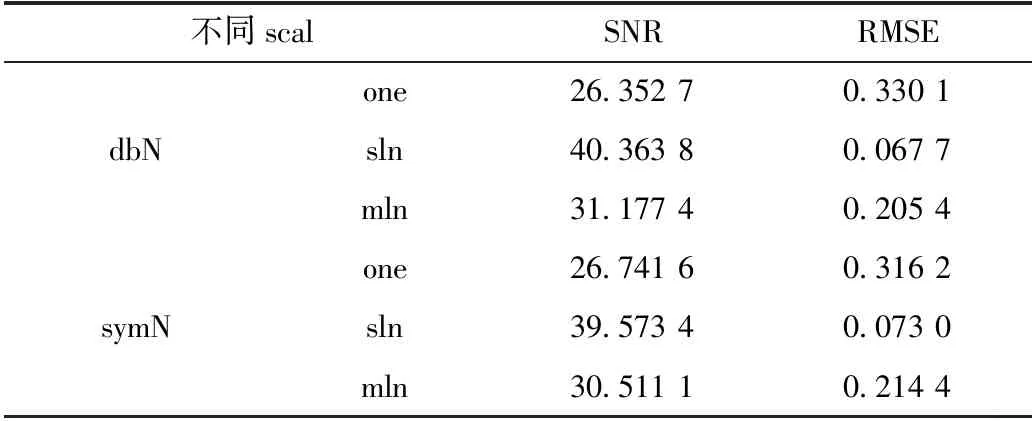
表1 不同scal的去噪效果对比

2.3 不同小波基函数对去噪效果的影响

分别采用小波函数dbN和symN对原始数据进行去噪。去噪结果见表2。从表2可知，db小波系的去噪效果优于sym小波系。

表2 不同小波函数的去噪效果对比

2.4 不同分解层次对去噪效果的影响

分别将监测信号分解成1～12层。去噪结果见表3。从表3可知，在dbN小波去噪过程中，随着分解层数的增加，SNR不断减小，RMSE不断增大，分解层数为1层时，SNR最大，RMSE最小。因此，本文选择lev=1。

表3 不同分解层数的去噪效果对比

2.5 不同小波阶数对去噪效果的影响

为确定小波阶数N，分别用db1～db10对监测信号进行去噪。结果见图4。从图4可知，在db小波系中，db5小波函数的SNR最高，去噪效果最好。因此，本文选取db5为小波去噪的基函数。

图4 不同阶数对去噪效果的影响

综上研究，本文采用以下方案对GCJ-01-07监测点的数据进行去噪分析。小波函数为db5，硬阈值处理方法，rigrsure阈值原则，scal选取sln，分解层数为1，去噪后的数据与原始数据的拟合图见图5。从图5可知，在35～50、55～60、70～90 d这3个时间段内，监测数据受噪声污染较大，监测曲线多出现尖峰点。经小波去噪后，监测曲线趋于平缓，更接近真实变形。

图5 原始数据与去噪后数据拟合

3 沉降预测分析

建立11-8-1的BP神经网络结构，即输入层单元数11个，隐含层单元数8个，输出层单元数为1个。将第1～30期监测数据作为学习集，通过Matlab软件编程实现BP神经网络算法，并将第31～40期监测数据作为测试集，用来验证预测模型的精准性。预测值与实际值的对比见表4。预测值与实际值拟合见图6。

表4 预测值与实测值对比

图6 预测值与实际值拟合

对比直接采用BP神经网络预测与先采用小波去噪再采用BP神经网络预测结果可知：①前者的预测值与真实值之间的误差在1%～3%，而后者的预测值与真实值之间的误差基本保持在1%之内；②直接采用原始数据预测时，预测值与真实值的相关性系数为0.849；采用去噪后数据进行预测时，预测值与真实值的相关性系数为0.989。由此证明，本文提出的小波去噪与BP神经网络预测模型是合理的。