拓扑数据分析在复杂脑网络分析中的应用

阴桂梅 王千山 姚 蓉 李海芳

（1.太原师范学院计算机系，山西晋中030619；2.太原理工大学信息与计算机学院，山西太原030024）

1 引 言

宇航员面临着我们大多数人永远都不会经历的精神和心理挑战，自从美国女宇航员莉萨·诺瓦克事件后，NASA 一直致力于研究降低宇航员在太空飞行期间的精神健康问题风险。航天器的工程技术实现能力是实现载人航天任务的基础，但宇航员需面临新的心理学和精神病学的挑战是主要的限制性因素。为此，本文将从宇航员的视角，运用拓扑数据分析中的持续同调理论，以精神分裂症数据为例，分析其复杂脑网络的持续拓扑特征，以便能够为提前预防和检测宇航员精神疾病提供有效的脑网络指标。

拓扑数据分析（TDA）［1］是一个数据分析、代数拓扑、计算几何、计算机科学、统计等多领域相关的一个领域。TDA 的主要目标是利用几何学和拓扑学的思想研究数据的定性特征。为了达到这个目标，TDA 需要精确的定义定性特性，还有在具体实践应用中的计算工具，以及保证这些特性稳定性、健壮性的理论。解决这几个问题的一种方法就是TDA 中的持久同源性（PH）理论。将PH理论运用于大脑网络分析是当前正在兴起的一个研究方向。

对大脑成像数据处理和分析时，一般都是通过生成表示节点之间连接强度的矩阵，然后选择合适的阈值对矩阵二值化最终生成邻接矩阵来构建脑网络。阈值的选择在网络构建中起着重要作用，因为它影响网络连接的密度和网络的拓扑结构。通常有三种网络阈值化方法［2］。

1） 选取单个阈值。一般选某个连接密度作为单个阈值，当阈值选取2lgN/N时，网络达到全连接，也就是网络中不存在孤立点。该方法只适用于随机网络，实际网络中没有意义；

2） 预定义阈值空间。该方法通常采用统计方法剔除伪连接或弱连接，间接达到选取阈值的目的。缺点是当数据变化时确定阈值过程复杂且不具备普适性，另外在删除的弱连接中可能会存在重要的信息传递路径；

3） 条件限制下的阈值空间。该方法要求在选取的阈值空间下所构建的脑网络具有小世界属性，若构建随机网络，则要求与原始网络具有相同的节点数和节点度分布，且节点的平均度应满足＞2lgN。

目前还有一些新的阈值化方法，如使用网络的最小生成树（MST）构建无偏网络，MST 对阈值和密度值不敏感，被认为是网络二值化的良好技术，但由于网络的MST 非常稀疏，会造成许多重要的本地连接被忽略［3］。还有基于热核高斯核的无窗口方法［4］，该方法可减少系统中虚假的快速变化大脑连接的状态空间，解决了滑动窗口法运用于动态脑网络分析时存在高频噪声问题。

虽然以上方法从不同的角度对于脑网络构建时阈值选择问题提出了解决方法，但是网络阈值的选择依旧没有金标准，为此本文将拓扑数据分析（TDA）方法中持续同源性（PH）理论引入脑网络分析中，该方法构建脑网络时无需阈值化，可以在全尺度范围内进行分析，可实现跨多个尺度提取脑网络中持续拓扑特征。

2 拓扑分析持续同调性理论

定义1 拓扑空间［1，5］:设集合X上的一个拓扑空间U是2X上的一个子集，即U⊂2X，如果满足下列条件:（1）Φ，X⊂U；（2）u1，u2⊂U，u1∪u2⊂U；（3）u1，u2⊂U，u1∩u2⊂U；则称（X，U） 为有限集X的拓扑空间。

定义2 单纯形［5］:设在实数域的n维向量空间Rn中，存在一组向量a0，a1，a2，…，an，使得｛a1-a0，a2- a0，…，an - a0｝ 线性无关。设E =｛θ0a0+θ1a1+…+ θnan｝θ0+ θ1+…+ θn =1，θi ＞0｝ ，点集E就称为一个n维单纯形。

0 维单纯形就是点；1 维单纯形就是线段；2 维单纯形就是三角形；三维单纯形就是立体三角形。

定义3 单纯复形:设Κ是单纯形的有限集合，若满足如下条件［1］:（1）若σ∈K，则Κ中任意一个单纯形的任意面仍属于K；（ 2） 对于σ1，σ2∈K，如果σ1∩σ2是空集，或者σ1∩σ2在σ1和σ2的公共面，那么称Κ为单纯复形。单纯复形K中单纯形维数的最大值称为K的维数，表示为

定义4 Rips 复形［6］:对于点云集合X，设d（，） 表示点云集合中两点的距离，那么R（X，λ） 为Rips 复形当且仅当其k维单形［x0x1…xk］ 满足d（xi，xj） ≤λ，0 ≤i，j≤k。

3 基于PH 的全尺度脑网络分析模型

根据持续同源数据分析方法［7］，结合脑电信号处理的特点，本文设计的全尺度脑网络分析模型如图1 所示。模型的输入是脑电时间序列信号，选取合适的度量空间后，脑电时序信号中的点就称为点云，在该空间构建点云的邻接矩阵，然后通过计算持续同调性获取持续拓扑特征，最后通过持续特征的稳定性分析确定网络的持续不变特征。

3.1 构造邻接矩阵

将经过预处理的EEG 时间序列信号输入模型，选择皮尔逊相关性度量空间，为EEG 信号各通道数据（即点云）构造连接矩阵。针对脑电信号的特点，实验构造的是无向加权网，电极通道为网络节点，也就是一维单纯形。

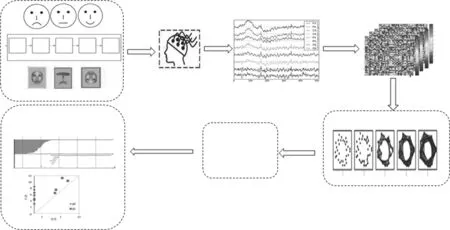
图1 基于PH 的全尺度脑网络分析模型框架图Fig.1 The framework of the whole-scale brain network analysis model based on PH

3.2 构造大脑网络复形

构造大脑网络嵌套复形的过程也就是计算持续同调的过程。持续同调分两部分，即同源性和持续性。同源在群论称作同调，它是拓扑集合分类的工具，可以度量一个单纯复形的特定结构；持续性是指给定一个ε，在ε所有可能值下计算哪些结构是持续存在的，即获得持续拓扑特征。特征中能够保持时间长的就是有用的特征，而寿命较短的可能是噪声，这个过程就称为持续同调。构造复形的关键步骤就是选择合适的过滤算法和过滤阈值ε。

3.2.1 过滤阈值ε 的选择

过滤阈值ε的选择非常重要，一般方法是通过选择不同ε构造复形，找到有效结果所对应的ε。如果ε过小，那么构造的复形就可能是原始的点云，或者点云的几条边；如果ε过大，可能的结果就是原始点云构成一个巨大的超维复形。

3.2.2 过滤算法的选择

针对不同实际的应用，需要构造不同类型的单纯复形，Vietoris-Rips complex 算法是基于图的过滤，非常适合应用于基于图论的复杂脑网络复形构造，并且对处理高维数据有很好的性能。本实验采用Vietoris-Rips complex 算法过滤。

3.3 持续拓扑特征的可视化

随着过滤阈值ε的变化，Rips 复形的拓扑特征会发生变化。过滤过程中网络的拓扑变化使用条形码或者持续性图可视化表示。在过滤过程中主要是计算p维贝蒂数间隔［εbirth，εdeath］ ，其中εbirth就是单纯复形中p维孔开始的时间，而εdeath是消失的时间，同时它们也是条形码中一个条形码的开始和结束点，这些间隔用图表示就是持续条形码。与条形码等效的是持续图。条形码中，横坐标表示持续特征出现的时间，即εbirth，纵坐标是持续特征消失的时间εdeath，将过滤过程中求得的间隔集合［εbirth，εdeath］ 作为持续图中点的坐标，将集合中所有的间隔对表示到坐标中就绘制了持续图。在条形码中，横坐标表示过滤阈值ε，用［εbirth，εdeath］ 的长度表示条形码的长度，条形码长度大的表示持续拓扑特征，条形码长度很短或者只是一个点的表示噪声，相对应的在持续图中，离对角线远的点表示持续特征，离对角线很近的点表示噪声。

3.4 持续拓扑特征的稳定性分析

拓扑特征的稳定性分析也就是条形码或持续图的统计分析问题。本实验选用方法成熟且适合脑网络分析的稳定性度量标准。常用的稳定性度量标准有Bottleneck 距离和Wasserstein 距离。如果对数据集的一个小扰动只会在该指标之前的持续图中造成一个小变动，说明该指标是稳定的。

定义5:设p∈［1，∞），两个图X和Y之间的p阶Wasserstein 距离定义为

式中:ø:X→Y——从X到Y的映射。

当p =∞时，距离d是二维空间的度量，以上公式表示为

式中:W∞［d］∞——Bottleneck 距离。

Bottleneck 距离度量两个图对应匹配点之间的最大距离，可以捕获持续图大的变化。Wasserstein距离度量的是两个图对应匹配点之间的总距离，可以提供持续图之间相似性的总体变化，它对持续图小的变化比较敏感。

4 实验及分析

4.1 实验数据及预处理

实验数据采用来自北京市回龙观医院精神分裂症工作记忆（WM）EEG 信号，经过重参考、分段、去除眼电、肌电等伪迹预处理，网络节点规模为60个，分5 个波段θ（4～7）Hz，α（7～14）Hz，β1（14～20）Hz，β2（20～30）Hz，γ（30 ～40）Hz。实验分三个阶段，每个被试每个频段每个阶段下，选取20 个平稳脑电信号拼接形成最终的EEG 时间序列。

4.2 基于PH 的邻接矩阵构建

本实验采用皮尔逊相关性度量空间构造邻接矩阵。将各节点间皮尔逊相关系数的倒数作为节点间连接的权重，得到60 ×60 无向加权网。精神分裂症工作记忆编码阶段不同稀疏度下构造的动态邻接矩阵如图2 所示，可得到如下结论。

图2 编码阶段不同连接密度下邻接矩阵示意图Fig.2 Adjacency matrixes at different connection densities in encoding stage

1）网络连接密度较小时（20%左右），健康被试和精分病人脑网络差异很大；

2）从网络连接密度50%左右开始，健康被试和精分病人的连接矩阵变化逐渐变小，说明健康被试和精分病人在工作记忆编码阶段的连接矩阵是有“形状”的，同时从图3 无阈值条件下构造的邻接矩阵也可以看到同样的结果。

4.3 构造精神分裂症WM 数据的单纯复形

实验采用斯坦福大学拓扑计算小组基于PLEX库［8］开发的软件包JavaPlex［9］计算。

图3 编码阶段不同频段及全频段邻接矩阵图Fig.3 Adjacency matrix at different bands and mean in encoding stage

构造复形需要确定四个参数（1）由边权矩阵构造的点云坐标文件（. txt）；（2） 最大过滤值；（3）最大维数；（4） 过滤步骤数（Filatration steps，简称Fs）。以下根据实验情况分别讨论如何确定这几个参数可以达到最佳实验效果。

1）由边权矩阵构造点云坐标文件

首先将邻接矩阵转换为边权矩阵，矩阵中每一行为“ijωij”，然后用度量映射（Isometric Feature Mapping 简称ISOMAP）算法［10］，将高维邻接矩阵中两两节点之间的距离在低维上（通常是2 维，也可以是任意维）找到一组新的样本点（即点云），使降维后两点间的距离与它们在高维上的距离相等。ISOMAP 算法既能够保留非线性数据的本身的几何结构，又能够保持全局的结构信息。

2）最大过滤值

构造边权矩阵后，分别取每个阶段各个节点之间距离的最大值作为实验最大过滤值，全频段及5个频段下的最大过滤值见表1。

表1 最大过滤值Tab.1 Max filtration value

3）最大维数和过滤步骤数

最大维数初值设定为3，也就是提取dim0、dim1、dim2 和dim3 四个维度下的持续拓扑特征。

过滤步骤数即过滤步长，根据文献［7］一般Fs=20，本实验取Fs=20，100，1 000 三种情况分别提取持续拓扑特征，来确定模型中最优Fs。实验结果见表2。

表2 三种过滤步骤数下实验结果比较Tab.2 Experiment results in three filtration steps

表2 中，运行时间是在计算机配置为CPU:Interl（R）core（TM）i7-6700；内存32G；操作系统WindowsX64 位机上运行得到的。从表2 可知，三种情况下构造的复形总数不变，第二种情况运行时间比第一种情况多消耗21.14%，但是特征数变化不大，第三种情况运行时间比第二种情况多消耗3.49%，特征数变化较大，因此数据量较大时，权衡时间效率和特征数，过滤步骤数可以选择20 或者1000。以下通过持续图可视化确定最终的过滤步骤数。Fs=20，100，1000 三种情况下健康被试持续拓扑特征的持续图如图4 至图6 所示。

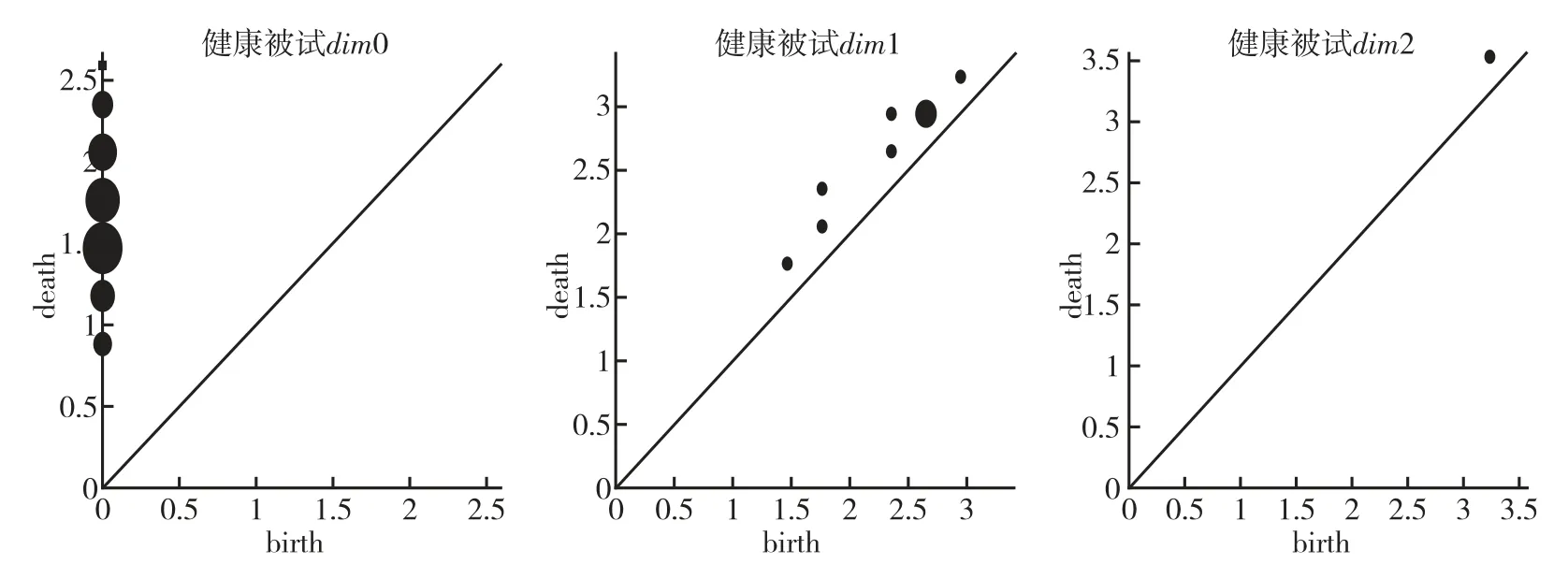
图4 健康被试编码阶段持续图（Fs=20）Fig.4 Healthy subjects' persistence diagrams（Fs=20）in encoding stage

图5 健康被试编码阶段持续图（Fs=100）Fig.5 Healthy subjects' persistence diagrams（Fs=100）in encoding stag

图6 健康被试编码阶段持续图（Fs=1000）Fig.6 Healthy subjects' persistence diagrams（Fs=1000）in encoding stage

从图6 可知，dim0 特征基本相同，dim1 和dim2两种情况，虽然Fs=100 和Fs=1000 时特征数变多，但这些特征多分布在对角线附近，也就是持续时间很短的噪声，只有间隔为［3.474274，3.709818］始终存在也就是持续拓扑特征。由此可以确定过滤步骤选Fs=20 效果最佳。同时从表2 可知，dim3 特征数始终是0，所以过滤的最大维数选择2。

4.4 精神分裂症WM 持续拓扑特征

根据以上实验确定的过滤参数（1） 最大维数2；（2） 各频段健康被试和精分病人最大过滤值对应取表1 中值；（3） 过滤步骤Fs=20，计算全频段、α、β1、β2、γ、θ 脑网络的持续特征，分别用条形码和持续图可视化。编码阶段精分病人全频段持续特征的条形码如图7 所示。

图7 精分病人编码阶段三个维度的条形码示意图Fig.7 Patients persistence barcodes in encoding stage

4.5 精神分裂症WM 持续拓扑特征稳定性分析

本实验采用Bottleneck 距离和Wasserstein 距离两个度量标准对持续图进行比较测度持续特征的稳定性。实验采用Python 环境下Ripser 调用GUDHI 包计算Bottleneck 距离和Wasserstein 距离。

1） Bottleneck 距离

计算Bottleneck 距离［10］的重要参数是精确度e。本实验e取两个值作比较，一个e=0.01，计算近似值，另一个e 取默认值，计算真实值，计算结果见表3。

表3 持续图间的Bottleneck 距离Tab.3 Bottleneck distances between diagrams

从表中可知，除dim0 的α频段和dim1 的γ频段外近似值和真实值之间的误差很小，可能这两个频段的持续拓扑特征存在奇异值。

2）Wasserstein 距离

健康被试和精分病人全频段和各个频段下两个维度的Wasserstein 距离［11］计算结果见表4。

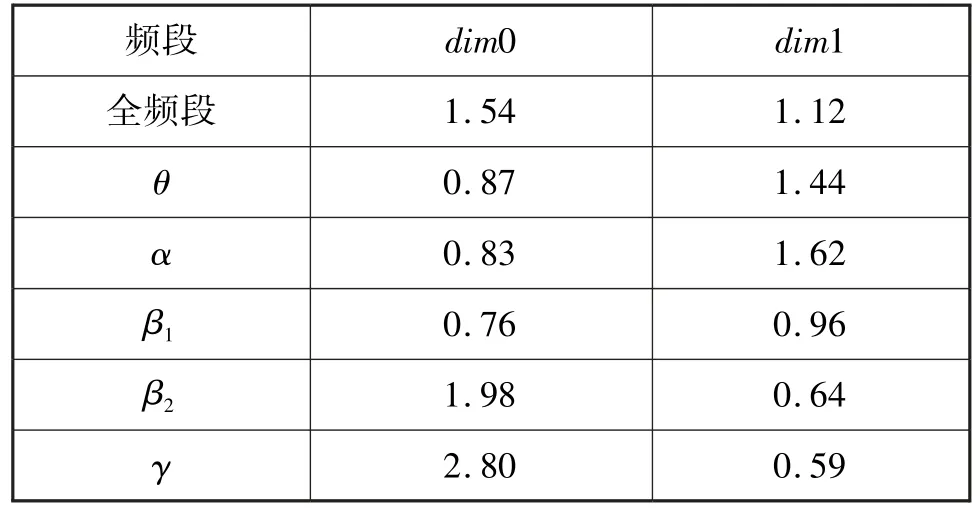
表4 持续图间的Wasserstein 距离Tab.4 Wasserstein distances between diagrams

4.6 结果分析

本文提出全尺度复杂脑网络模型并应用于精神分裂症病人WM 数据分析中，经实验分析确定模型中的重要参数和算法，在边权矩阵和点云文件互换时，运用ISOMAP 算法降维后，矩阵由60 维基本上降到了34～38 维之间，为后续高效率处理数据提供了良好的基础。

通过全方位的实验效果比较确定几个重要参数:1） 最大维数为2；2） 实验表明健康被试β2，θ和γ三个频段在dim2，精分病人β2、和γ两个频段在dim2 都无持续拓扑特征，所以在稳定性分析时，实验只分析dim0 和dim1 两个维度；3） 最大过滤步骤为Fs=20 既不丢失重要特征，又可剔除噪声，同时还可提高时间效率。

在稳定性分析中，持续图间的Bottleneck 距离结果显示，精确度参数e采用默认值实验效果更接近真实值，但当持续图没有奇异值时真实值和差异值差别不大。另外，在α和θ频段Bottleneck 距离较小，也就是健康被试和精分病人的持续图大的变化较少，可以选取这两个频段的持续拓扑特征作为模型的输出。

5 结束语

本文提出基于持续同调性的全尺度脑网络分析模型，并对模型中的每一数据处理步骤涉及到的算法和参数做了分析，研究了全尺度脑网络构造中的节点、边权矩阵构造、过滤阈值的选择等关键性问题。并将模型应用于精神分裂症WM 持续拓扑特征分析中，获取持续拓扑特征，并分析其稳定性。实验结果表明本文提出的模型具有稳定性和抗噪性，可以为精神类疾病医学影像分析提供稳定的生物参考指标。