一种基于莱维飞行的新型改进平衡全局优化算法

杨柳庆 杨婷婷 王鹏飞 张 勇

（1.南京航空航天大学无人机研究院，江苏南京210016；2.南京航空航天大学中小型无人机先进技术工业和信息化部重点实验室，江苏南京210016；3.南京航空航天大学自动化学院，江苏南京210016）

1 引 言

科学和工程应用中的大部分优化问题都非常复杂，具有挑战性。传统方法倾向于使用特定问题的信息指导产生解决方案，因此传统方法是高度特色化的，普适性不强，传统方法具有线性编程和凸优化［1］的特点，同时有很多缺陷和不足，比如解决问题过程极其复杂、易陷入局部最优解。传统方法已经很难解决当前面临的工程应用问题，当前的趋势之一是使用元启发式算法，该算法大多数源于各种自然现象，可分为基于自然进化（EA）的算法、基于物理学技术的算法和群智能算法（SI）三大类。其中，最受欢迎和最具代表性的算法是群智能算法中的粒子群优化算法［2］（PSO）和蚁群优化算法（ACO）［3］。除了这两种算法，还有很多有效的元启发式算法，这些算法的特点是计算简单、不需要使用优化问题的派生信息，而且能在不改变算法结构的情况下解决多种类型的优化问题。

平衡优化算法（EO）［10］是Afshin Faramarzia 和Mohammad Heidarinejad 于2020年提出的一种基于物理学技术的算法，受动态资源和库模型的启发，该算法用于估计平衡状态。算法基于控制体积的动态质量平衡，其中质量平衡方程根据各种资源库模型来描述控制体积中非反应性成分的浓度。莱维飞行策略有助于在探索和开发之间获得更好的平衡，并且在很大程度上可以防止陷入局部最优解。因此，本文提出一种基于莱维飞行的改进EO算法，称为LEO，其目的在于对EO 进行优化，提高EO 的收敛速度和最优解的质量。LEO 经过23 种基准函数模型进行了测试和仿真，并与其它5 种元启发式算法进行比较，仿真结果表明LEO 可行且有效，在性能方面比EO 有较大提升。

本文详细介绍了原始平衡优化算法和莱维飞行的飞行轨迹，描述了LEO 的研究细节。建立了新型全局优化算法LEO 的数学模型和算法流程，采用23 种基准函数模型对LEO 算法进行实验验证，并对实验结果进行论证、分析和总结。

2 平衡优化算法和莱维飞行策略

2.1 平衡优化算法

平衡优化算法是一种新提出的元启发式算法，其灵感来源于在控制体积上进行简单混合的动态质量平衡。在平衡优化算法中，粒子类似于溶液，浓度类似于粒子优化算法（PSO）中粒子的位置。使用质量平衡方程来描述控制体积中非反应性成分的浓度，该浓度取决于各种源汇机制。质量平衡方程为控制体积过程中物体进入、离开和生成的质量守恒提供了基本物理原理。质量平衡的通用方程式由式（1）给出的一阶常微分方程表示

式中:V——控制体积；C——控制体积浓度；Ceq——在控制体积内没有任何生成的平衡态浓度；G——质量生成速率；——质量变化速率；Q——流入和流出控制体积的体积流量。

其中，F可用于估算已知流失率对照体积的浓度，或者用于计算具有已知发生率和其它条件的简单线性回归的平均流失率。

平衡状态是算法的收敛状态，并且希望是所考虑问题的全局最优解。在优化过程的初始状态，平衡浓度是未知状态，平衡候选对象为粒子提供了搜索模式。根据在多种类型优化问题下进行的不同实验，将候选对象确定为优化过程中的四个最佳粒子，四个粒子浓度的算数平均值组成平衡池。这四个候选对象，即四个浓度有助于提高EO 的探索能力，算术平均值有助于提高EO 的开发能力。平衡池的向量表示为

2.2 莱维飞行

莱维飞行是一种随机游走类型，服从莱维分布的随机搜索方法，是一种短距离的搜索和偶尔较长距离的行走相交叉的行走方式，这种行走方式可以使得莱维飞行具有较好的全局搜索能力。莱维飞行轨迹最初是由Lévy 提出的，后来Benoit Mandelbrot 对其进行了详细描述。莱维飞行策略已经被广泛应用于优化问题和最优搜索，具有广阔的发展前景。

利维飞行是一种步长服从利维分布的随机游走类型，其分布方程为

其中，λ=1 +β，利维飞行是随机行走的一种特殊类型，其步长的概率分布服从重尾分布，将利维飞行步长s定义为

u和υ定义如下

其中，α0=0.01，β=3/2；u和υ从正态分布μ=中选择。

3 基于莱维飞行的改进平衡优化算法

平衡优化算法（LEO）在解决单峰优化问题时表现良好，但是在处理多峰优化问题时，EO 获得的解决方案并不理想。可以发现EO 具备较好的开发能力和收敛速度，但容易陷入局部最优解，全局搜索能力不强，收敛性不高，因此，本文提出一种改进的平衡优化算法（LEO）。莱维飞行可以使搜索代理的多样性最大化，这样既能保证算法的全局搜索能力，又能防止算法陷入局部最优解，即莱维飞行轨迹有助于EO 在探索能力和开发能力之间取得更好的平衡。改进的平衡优化算法使用莱维飞行轨迹来更新位置，表示如下

必须指出，sign（rand-1/2）只有3 个有效值分别为:1，0 和-1。Levy表示莱维飞行的随机游走方程。

本文的改进策略，即在EO 中加入莱维飞行策略，有助于基本的EO 跳出局部最优值，莱维飞行轨迹的步长通常是很小的，但有时会出现较大的步长，因此，从长远来看，加入莱维飞行策略可以确保粒子可以有效地在搜索空间里进行搜索，提高粒子的搜索能力。同时，这种方法可以增加EO 解决方案的多样性，提高算法的全局搜索能力，对于单峰和多峰基准函数来说，改进的EO 可以提供更有意义的结果。改进的EO（LEO）流程图如图1 所示，其在解决优化问题中的性能将在第4 节中通过基准函数和仿真实验来进行验证。

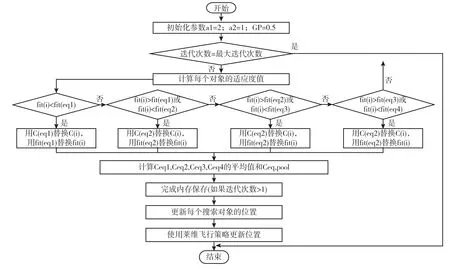
图1 LEO 流程图Fig.1 LEO flow chart

4 仿真实验

为了更好地验证LEO 的性能，第4 节内容设计了无约束的优化问题测试实验，对LEO 进行全面地研究分析。实验选取23 个基准函数分别进行测试，并与其它几种智能优化算法的结果相比较。

高维基准函数具体参见文献［11］，包括高维单峰基准函数（f1～f7）和高维多峰基准函数（f8～f23），高维单峰基准函数只有唯一的全局最优解，可以有效测试算法的开发和收敛性，而高维多峰基准函数则具有更多的局部最优解，用于测试算法跳出局部最优解的能力。因此，算法的探索能力和避免局部最小值的能力可以由多峰函数来测试，见表1 和表2。

表1 高维基准函数Tab.1 High-dimension benchmark functions

表2 低维基准函数Tab.2 Low-dimension benchmark functions

表1 中，由于函数f1～f7特性类似，因此表1 只显示f1为例，f12和f13特性类似，表中只显示f13。表2 中，由于函数f15～f17特性类似，因此表1 只显示f15为例，同样的，f21～f23特性类似，表中只显示f23。

为了对LEO 的测试结果进行全面的分析，实验选取其它4 种智能算法进行对比，算法的主要参数设置见表3。为了保证测试的有效性和准确性，每种算法在单个基准函数上分别独立运行30 次，记录运行结果的最优值、最差值、平均值和标准差，所有的算法根据其标准差的大小进行排序，此种排序方式可以看出哪种算法的运行结果更加稳定。

表3 比较算法参数设置Tab.3 Comparison algorithm parameter settings

表3 中，EO 算法中a1是表示控制搜索能力的常数，a2表示算法的搜索能力，GP表示生成概率。GWO 中，a表示收敛参数，t和T 分别表示当前迭代次数和最大迭代次数。PSO 中，wmax和wmin分别表示最大和最小惯性权重，c1和c2分别表示认知常数和社会属性常数。

高、低维基准函数的测试结果分析见表4 和表5，总结了5 种算法在高维基准函数中独立运行30次获得的最优、最差、均值和标准差的统计结果受版面限制，表4 中只展示f1～f3和f5～f12的结果（f3和f4结果基本相同），表5 中只展示f14～f22的结果。其中f1～f7为高维单峰函数，没有局部最优解，因此适用于测试算法的收敛速度。在表中可以看出，LEO 在单峰基准函数中表现出极佳的性能，能比其它算法更有效地找到最优解。LEO 在f1、f2、f6、f7中的表现优异，其标准差也小于其它算法。在f5中，LEO 相比其它算法准确地找到了最优解，但标准差比GWO 大。可以看出GWO 在优化f3和f4方面比LEO 具有更好的效果，LEO 的表现基本处于第3 的位置。

f8～f13为高维多峰基准函数，具有多个局部最优解，可用于检测函数跳出局部最优解的能力。从表5 中可以看出，在f9～f14中，LEO 表现出的性能都远高于其它4 种算法，不仅能比其它算法更有效地找到全局最优解，而且标准差也小于其它算法。总体来看，不论单峰函数还是多峰函数，所有的统计结果都显示LEO 的优越性能。

表4 高维基准函数测试结果Tab.4 High-dimension benchmark function test results

续表4

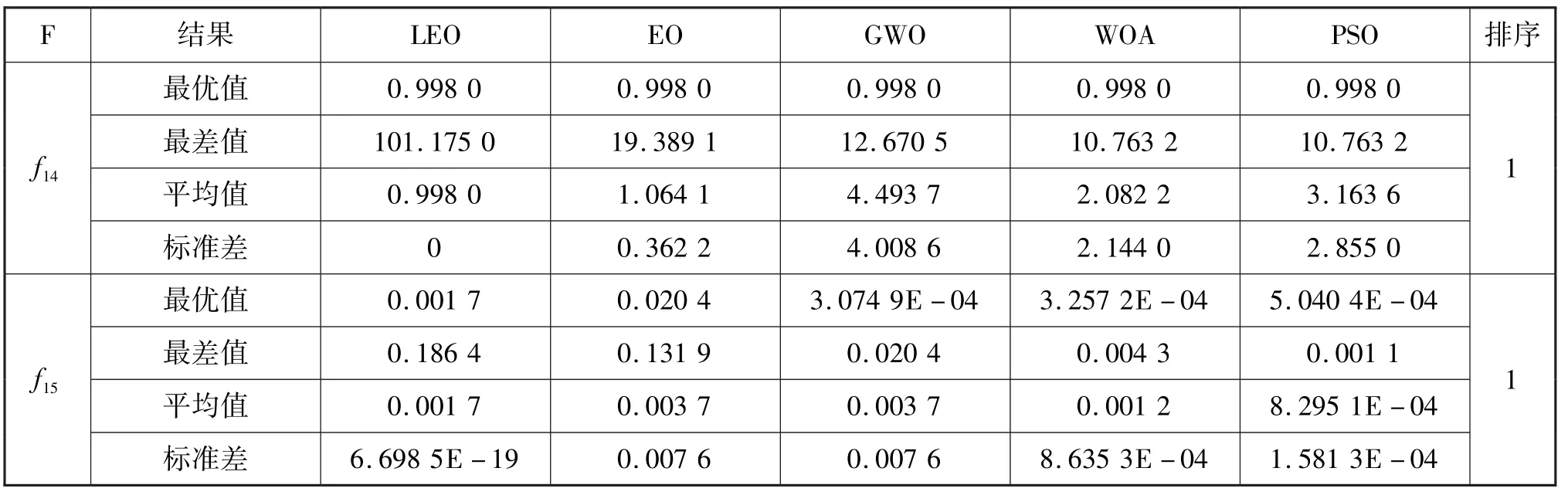
表5 低维基准函数测试结果Tab.5 Low-dimension benchmark function test results

续表5

5 结束语

本文将莱维飞行（Lévy flight）和平衡优化算法（EO）相结合提出一种新型的全局优化算法（LEO），并给出了新型全局优化算法的数学模型和算法流程。新算法保证了算法中全局搜索和局部开发之间平衡性，具有跳出局部最优解的能力。将该算法应用于基准测试函数求解以测试算法性能，通过与主流智能算法对比，优化结果表明新算法在解决优化问题方面表现更为优越，该算法后续将应用于无人机航路规划和任务分配等工程问题。