为什么要引入复数

二、虚数的争议

虚数产生之后，在数学界引起了巨大的争议，主要分成三派.一派认为虚数是存在的，比如微积分的先驱者之一沃利斯，他试图用几何方法解释虚数.另一派是以数学家笛卡尔为代表的学派，他们不承认或反对虚数，认为虚数是想象的、虚构的.第三派是以莱布尼茨为代表的学派，莱布尼兹在1702年曾说：复数“犹如存在和不存在的两栖物”.

虚数的名称是笛卡尔给出的，他不能接受复根.于是，在他1637年出版的《几何》这本书中解释复根时说“但它们始终是虚的”.在数学发展史上，欧拉是第一个使用虚数符号i来表示√-1的，并写在他1777年提交给圣彼得堡科学院的论文中，这篇论文直到1794年才发表，那是在欧拉逝世后11年.但是，欧拉并没有确切地掌握复数运算，在他1770年出版地《代数》一书中认为√（-1）·√（-4）=√（-1）·2=2，其中理由是√a·√b=√ab.欧拉尽管在许多地方用了虚数，但又说：“一切形如，√（-1），√（-2）的数学式子都是不可能有的，想象的数，因为它们所表示的是负数的平方根.对于这类数，我们只能断言，它们既不是什么都不是，也不比什么都不是多些什么，更不比什么都不是少些什么，它们纯属虚幻.”

欧拉

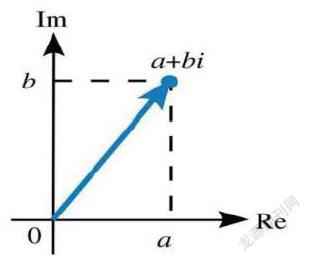
有了虚数的符号，就可以定义复数了，用C表示复数的集合.虚数与实数一起组合成了复数.复数通常用a+bi的形式表示，其中a和b都是实数，而i=√（-1），也称为“虚数单位”.实数a叫做复数的实部，而b叫做复数的虚部.实数可以被认为是虚部为零的复数.

与实数不同，在复数集合中不存在大小关系，也就是说两个复数之间不能比较大小.这并不以外，因为任何数对（包括向量）都不能在通常意义下比较大小.但是，复数集合却包含实数集合，因为只需要在复数中令虚数i前面的系数为0就可以了.对复数可以定义运算.

三、复数的解释

高斯

那么复数在现实中怎么可视化呢？最早发现这个问题的是数学家韦塞尔（Wessel），他给了复数几何和向量的解释，使得复数能通过XY平面实现可视化.后来高斯在1831年也提出这样的平面表示法，系统地完善了复数理论，他第一次提出了“复数”这个名词，还将表示平面上同一点的两种不同方法——直角坐标法和极坐标法加以综合，统一于表示同一复数的代数式和三角式两种形式中，并把数轴上的点与实数一一对应，扩展为平面上的点与复数一一对应.高斯不仅把复数看作平面上的点，而且还看作是一种向量，并利用复数与向量之间一一对应的关系，阐述了复数的几何加法与乘法，如图.

四、复数的结构

复数中包含了群、环、域、线性空间等结构.加减乘除运算法则和实数域中的一样，有交换律、结合律、分配律.不同的地方是，复数可以进行开方运算，后来逐渐发展出了四元数、八元数等.但四元数的乘法运算中不再有交换律;八元数的运算中连结合律都没有.

实数域中有一个重要的结构：序结构，可以用来比较两个数的大小.对于复数，虽然可以给它一个序，但是这个序一定不会和代数结构相容，就是与域结构不相容.所谓与域结构相容（即有序域）就是说，对于序a

复数域与实数域的维数也不同，一个是1维，一个是2维.复数中还有共轭结构.复数中的代数、几何、拓扑、分析结构以及复合结构，是最基本、最简单的具有复合结构的复流形及复李群.

五、复数的奇妙之处

复数起初可能看起来很奇怪，但我们完全可以把虚单位i看作一个代数，把复数的加减乘除看作一元多项式的加减乘除.例如，对复数进行加减，你只需把实部和虚部彼此结合起来即可，这类似于对多项式进行合并同类项;复数的乘法，可以借助適用于分配律来完成的.对于除法，我们完全可以将其转换为乘法，只不过乘上去的是除数的倒数.

跟实数一样，复数的乘法遵循乘法交换律，这意味着当你以任意顺序乘以两个复数时，其结果是相同的.此外，复数的乘法也遵循乘法结合律，这意味着将两个以上的复数相乘时，你可以自由选择先乘哪一对.

虚数的引入，开启了一个全新的数学世界.这是一个奇怪的世界，平方可以是负的，但是它的算法与我们熟悉的实数非常相似.但对实数的扩展，这只是一个开始.

高斯引进复整数解决了两个数的平方和问题，即哪些正整数可以表示成两个整数的平方和，有多少表示方法？因为一个整数写成a2+b2，那就等于a+bi乘上a-bi，后来他证明这种数有跟整数类似的性质：任何一个自然数都可以分解成素数的乘积.利用这样一个基本的虚数关系就把两个数的平方和问题完全解决了.

库默尔（Kummer）通过引入分圆域（有理数域添加单位根这样的虚数而生成的数域）来研究费马大定理，这是代数数论的一个源头.上世纪90年代解决费马大定理，要用到模形式、椭圆曲线，这也是离不开复数的.这个猜想看上去是和复数一点关系也没有，但到最后解决它仍离不开复数.

陈省身

陈省身先生说过，复数的引进是数学史上的一件大事情.第一届菲尔兹奖获得者阿尔福斯（Ahlfors）也说，对精准函数作分析，通常需要考虑它们在复数域上的性质，因为复数域是一个代数闭域.求3次方程的根在实数域上求不出，用虚数自然就能求出.这是一个很重要的思想.

六、“虚数”不虚

“虚数”不虚也反映了一个非常重要的一个理念，就是“无用之用”.在最初研究复数时，人们觉得它没有实用，但现在应用非常广泛.在前苏联，拉夫连季耶夫（Лаврентьев）和沙巴特（Шабат Б）写了一本书《复变函数论方法》.两位杰出的数学家在这本书里举出很多例子，反映了复变函数的重要应用，包括在流体力学、气体动力学、弹性力学、电磁学、电工学、电路计算、机翼设计等方面.

爱因斯坦狭义相对论在阐述四维时空中的距离时，引入虚数，更容易让人接受;在电磁学、通信领域引入虚数更容易理解.当然这些理论，不一定非要引入虚数来解释.但是量子力学不得不引入虚数了，根据海森堡不确定性原理，没有进行观测时，单个原子所处的位置是不确定的，引入虚数后计算电子位置的概率，概率分布用具有复数值的波函数来表示的.

通过添加一个或多个“虚构”的数，我们可以把实数拓展为复数、四元数和八元数.这些数系看似远离了现实，但是它们能给我们带来思考数学世界的新的方式，而且，我们总能给它们找到用武之地.

随着科学和技术的进步，复数理论已越来越显出它的重要性，它不但对于数学本身的发展有着极其重要的意义，而且为证明机翼上升力的基本定理起到了重要作用，并在解决堤坝渗水的问题中显示了它的威力，也为建立巨大水电站提供了重要的理论依据.

经过许多数学家长期不懈的努力，深刻探讨并发展了复数理论，才使得在数学领域游荡了200年的幽灵——虚数揭去了神秘的面纱，显现出它的本来面目，原来虚数不虚呵.虚数成为了数系大家庭中一员，从而使实数集扩充到了复数集.