钢-混凝土组合梁与钢筋混凝土梁的设计差异及分析
2021-01-13田傲霜
◎田傲霜
一、引言
钢-混凝土组合梁与钢筋混凝土梁以其良好的结构性能,广泛应用于建筑工程、桥梁工程、公路与城市道路工程以及海洋工程等土木工程领域。与工程中传统的钢筋混凝土梁相比,组合梁的优良性能和技术经济指标使其在我国有着更广泛的应用前景。本文通过对比两种类型梁的力学强度分析和变形性能验算,为工程人员的设计和施工提供参考。
二、两类梁的受弯承载力设计计算
就设计理论而言,钢-混凝土组合梁和现浇结构中钢筋混凝土梁都可视为T 形截面梁。组合梁是通过剪力连接件达到与混凝土板的有效连接,连接件用以抵抗钢梁和混凝土板之间的相对滑移,使它们的弯曲变形协调,在弯矩作用下组合梁的截面的应变接近平截面假定,这样,钢梁和混凝土板之间就形成了一个具有公共中和轴的组合截面;而对于现浇结构中的钢筋混凝土梁,则是通过一次性整体现浇而成,依靠钢筋混凝土板与钢材之间粘结力和握裹力天然连接,协同受力。
在基本假定方面,两类梁均需满足以下几点:1.截面应变保持平面;2.不考虑混凝土的抗拉强度;3.混凝土受压区的应力与应变关系曲线按下列规定取用:
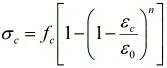
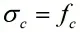

对于钢筋混凝土梁还有另外两条基本假定,分别为:纵向受拉钢筋的极限拉应变取值为0.01;纵向钢筋的应力取钢筋应变与其弹性模量的乘积,但其值应符合下列要求:。对于组合梁,对应的要求则与钢梁相同。
与钢筋混凝土梁相比,组合梁按照弹、塑性理论采用不同计算方法时,基本假定仍有不同,在弹性受弯承载力计算时的基本假定还有:在正弯矩作用下,不考虑混凝土板中的钢筋作用;中间支座两侧负弯矩区混凝土板受拉开裂区段的长度,各为该跨的0.15倍,在确定截面刚度时,只计入该区段的钢筋,不计入该区段的混凝土板。在塑性受弯承载力计算时,对于有混凝土板托的组合梁,不考虑混凝土板托的作用。
另外,施工方法对组合梁的受力性能有重要影响,(一)施工时钢梁下不设置临时支撑的组合梁,计算分析时应分两个阶段考虑:在施工阶段,即在混凝土板强度达到75%的设计强度之前,钢梁自重、混凝土板的自重和施工荷载由钢梁单独承担,并按《钢结构设计规范》(GB50017-2017) 进行计算;在使用阶段,即当混凝土板的强度达到75%的设计强度后,用弹性分析方法计算承载力时,使用荷载和第二阶段增加的恒载由组合截面承担,钢梁的应力和挠度应与前一阶段的应力和挠度叠加;采用塑性理论分析时,则全部荷载均由组合截面承担。(二)施工阶段在钢梁下设置临时支撑时,撤去支撑前钢梁不产生挠度,可以近似认为钢梁在施工阶段不产生应力,因此不必进行施工阶段的验算。而在使用阶段,即撤去临时支撑后,全部的恒载和使用荷载均由组合截面承受。而对于现浇结构钢筋混凝土梁施工时必须采用临时支撑。
钢-混凝土组合梁和现浇结构钢筋混凝土梁的应力-应变图相似。
钢筋混凝土梁在计算时要求满足:M≤Mu
式中:M 为弯矩设计值;Mu为截面受弯承载力。
对于钢-混凝土组合梁按弹性方法设计时,要求:

式中:σs为荷载效应设计值在钢梁截面内不利点处引起的正应力,受拉为正;
σc为荷载效应设计值在混凝土板截面内不利点处引起的正应力,受拉为正;
σst为荷载效应设计值引起的纵向受拉钢筋的应力;
按塑性方法设计时,组合梁的受弯承载力的极限状态方程为:Md≤Mu
式中:Md为弯矩设计值;Mu为截面受弯承载力。
钢-混凝土组合梁与钢筋混凝土梁的应力-应变图都分为受压区和受拉区两部分,但在进行简化计算时,对于钢筋混凝土梁受拉区、受压区的应力变化是连续的,对于组合梁由于底部有压型钢板的存在,其应力不连续。
可以得出:钢-混凝土组合梁与钢筋混凝土梁计算原理类似,但是具体计算公式差别较大。
三、两类梁的受剪承载力设计计算
在设计理论上,钢-混凝土组合梁和现浇结构的钢筋混凝土梁的竖向受剪承载力都是由计算和构造来满足的。对于组合梁而言,剪力主要由钢梁承担,而钢筋混凝土梁的剪力主要由箍筋来承担。另外,组合梁的受剪承载力取决于混凝土板竖向受剪承载力和钢梁的竖向受剪承载力,而对于钢筋混凝土梁则需要考虑混凝土抗剪切强度和箍筋抗剪切强度。
在基本假定方面,钢-混凝土组合梁和钢筋混凝土梁的抗剪承载力设计都沿用前面关于受弯承载力的基本假定,故二者异同见受弯承载力关于基本假定的分析对比。
组合梁的受剪承载力分析按照弹性理论和塑性理论分别阐述:
按弹性理论设计时,对于钢梁部分,剪应力的极限状态方程为:
式中:τs为组合截面钢梁部分在竖向剪力设计值作用下验算点处的剪应力;为钢材的抗剪强度设计值。
按塑性理论设计时,对承受正弯矩的组合梁截面或承受负弯矩且的组合梁截面,其竖向受剪承载力的极限状态方程可写为:vd≤Vu
式中:vd为竖向剪力设计值;Vu为截面的竖向受剪承载力。
而钢筋混凝土梁的受剪承载力极限状态方程为:Vcs≤Vu
式中:Vcs为竖向剪力设计值;Vu为截面的竖向受剪承载力。
由以上极限状态方程可以得出:按塑性理论设计时,钢-混凝土组合梁与钢筋混凝土梁的极限状态方程是相似的,而按弹性理论设计时组合梁需分别考虑钢梁的剪力设计值与混凝土的剪力设计值。
由于钢-混凝土组合梁和钢筋混凝土梁的材料形式的区别,故在抗剪承载力的计算公式上也有较大差异,组合梁的计算公式相对繁琐。
四、弯剪相关性
钢筋混凝土梁对弯矩和剪力的相关影响没有专门的要求。在弯矩和剪力的共同作用下,剪力对钢-混凝土组合梁的受弯承载力有不利的影响。对简支组合梁来说,考虑到在一般情况下Vd/Vu值不会很大,因此,我国现行《规范》中对弯矩和剪力的相关影响没有提出专门的要求。对于连续组合梁的负弯矩区,由于弯矩和剪力均达到最大,考虑弯矩的相关影响就显得比较重要。但实验表明,中间支座截面混凝土板内因为有纵向钢筋的存在,其竖向受剪承载力有可能高于钢梁腹板的极限抗剪能力。受剪承载力提高的程度取决于纵向钢筋拉力与钢梁拉力的比值γ=Fst/Fs,在γ 值较大的情况下,组合梁的竖向承载力可提髙 35%左右。根据试验结果,只要纵筋拉力与钢梁拉力的比值γ≥0.15,可以分别按纯弯和纯剪进行设计。
五、裂缝宽度和挠度验算
钢-混凝土组合梁和钢筋混凝土梁的裂缝宽度与挠度验算都是对正常使用极限状态的验算。对于组合梁来说,在承载力极限状态下进行设计计算时,无论采用弹性分析法还是塑性分析法,正常使用状态的内力分析均应采用弹性分析法。
对于组合梁和钢筋混凝土梁,按正常使用极限状态的验算要求,裂缝宽度应满足:ωmax≤[ωmax]
式中:ωmax为标准荷载作用下连续组合梁负弯矩区的最大裂缝宽度;
[ωmax]为《混凝土结构设计规范》规定的允许最大裂缝宽度。
但是二者关于挠度的验算则有不同。对于组合梁,按照正常使用极限状态的验算要求,挠度应满足:△≤[△]
式中:△为标准荷载作用下组合梁的跨中挠度;
[△]为《钢结构设计规范》规定的挠度允许值。对于钢筋混凝土梁,其挠度验算公式为:


S 是与荷载形式、支撑条件有关的挠度系数;
Mk为弯矩的标准组合值。
六、结语
综上所述:钢-混凝土组合梁与钢筋混凝土梁在受弯承载力、受剪承载力、弯剪相关性以及裂缝宽度和挠度计算方面既有相似性又有所不同。在进行设计时,除依据现行相关《规范》进行计算外,还应根据实际情况,将两种类型梁的优势充分结合,使其在结构中合理发挥各自作用。除文中提到的性能指标外,组合梁的设计还应考虑剪力连接件的抗剪承载力、组合梁中混凝土板的纵向受剪承载力、组合梁的整体稳定和局部稳定验算等问题。可以预见的是,随着试验研究和实际应用的不断发展,钢-混凝土组合梁将迅速推广而成为继钢筋混凝土梁之后,广泛应用于土木工程领域的结构构件。
