TASS1 算法的不可能差分区分器搜索*

2021-01-13李艳俊

密码学报 2020年6期

李艳俊, 林昊, 孙莹, 梁萌

1. 北京电子科技学院, 北京100070

2. 密码科学技术国家重点实验室, 北京100878

1 引言

随着社会网络信息化的快速发展, 信息安全问题变得尤为突出. 密码算法一直是信息安全中最核心、最关键的技术, 在维护国家政治稳定、经济繁荣中起到了强有力的保障作用, 在很大程度上为国家的国防安全、军事发展提供了坚实支撑. 进入21 世纪以来, 各个国家都在积极进行密码算法标准化工作建设, 美国于1997 年启动AES 计划, 并在2001 年确定了Rijndael[1]算法为其数据加密标准. 继美国提出AES计划后, 欧洲于2000 年启动了NESSIE 计划, 并于2003 年确定了Camellia[2]、MISTY1[3]、SHACAL-2[4]三个分组密码算法连同AES 作为欧洲新世纪的分组密码标准算法. 同时日本于2000 年4 月启动了CRYPTREC 密码评估项目, 并于2003 年5 月公布了他们评选出的密码, 推荐的分组密码除了上述的几种分组密码, 还包括日本研究人员设计的CIPHERUNICORN-E[5]和CIPHERUNICORN-A[6],Hierocrypt-L1[7]和Hierocrypt-3[8], SC2000[9]. 韩国于2004 年确定了ARIA[10]算法为其分组密码标准(KS X 1213). 中国国家密码管理局于2006 年1 月公布了无线局域网产品中适用的建议密码算法, 其中包括SMS4[11]分组密码.

为了更好地维护国家网络和信息安全, 加快我国密码标准化、本土化的发展, 推动我国密码理论和应用研究, 促进密码算法设计和实现技术进步, 培养密码人才成长, 中国密码学会于2019 年举办了全国密码算法设计竞赛. TASS1[12]就是第一轮22 个参赛的分组密码算法之一.

TASS1 分组密码算法支持128 和256 比特两种分组长度, 支持可变长度的密钥规模. 基于广义Feistel 结构设计, 算法迭代轮数为7 轮, 每轮7 步, 共49 步. 算法轮函数包括寄存器递归变换和轮密钥加, 特色之处在于引入了“随机池” 的概念, 即非线性部件采用密化随机池查询: 对于TASS1-128, 随机池是一个4 进32 出的查找表; 对于TASS1-256, 随机池是一个4 进64 出的查找表. 初始随机池公开, 在算法加密开始前随机池会和主密钥相互作用, 生成加密所需的密化随机池和8 个轮密钥.

差分密码分析[13]是Biham 和Shamir 于1991 年提出的, 他们利用这种方法攻击了DES 密码算法, 其主要思想是通过分析特定明文对的差值对密文对差值的影响来恢复某些密钥比特的信息. 不可能差分密码分析是差分密码分析的特殊形式, 最早由Knudsen[14]和Biham[15]分别独立提出, 其核心思想就是连接两段概率为1 的差分路径, 而这两段差分路径在“连接处” 是矛盾的. 利用这种矛盾的性质, 可知导致这些差分路径的密钥均为错误密钥, 将这些错误密钥排除, 从而得到正确密钥.

本文对TASS1 算法做的主要工作包括以下三个方面:

(1) 根据TASS1 算法的加密特性, 通过控制差分尽可能迟的到达高4 位来控制差分的扩散速度, 之后对差分比特单元建立大规模线性方程组求解得到TASS1-128 的19 步概率为1 的差分特征, 基于该差分特征构造40 步不可能差分区分器.

(2) 基于同样的思路, 通过建立大规模线性方程组求解得到TASS1-256 的40 步概率为1 的差分特征, 在此基础上, 构建TASS1-256 的82 步(全轮为49 步) 不可能差分区分器.

(3) 给出了对于TASS1 算法在设计方面、安全性方面的一些建议.

本文整体结构如下: 第2 节介绍了TASS1 算法及其符号说明; 第3 节给出了TASS1-128 的差分特征, 并基于该差分特征构建不可能差分区分器; 第4 节给出了TASS1-256 的差分特征, 并基于该差分特征构建不可能差分区分器; 第5 节总结全文并给出了对于TASS1 算法设计方面、安全性分析方面的建议.

2 TASS1 算法介绍

2.1 符号说明

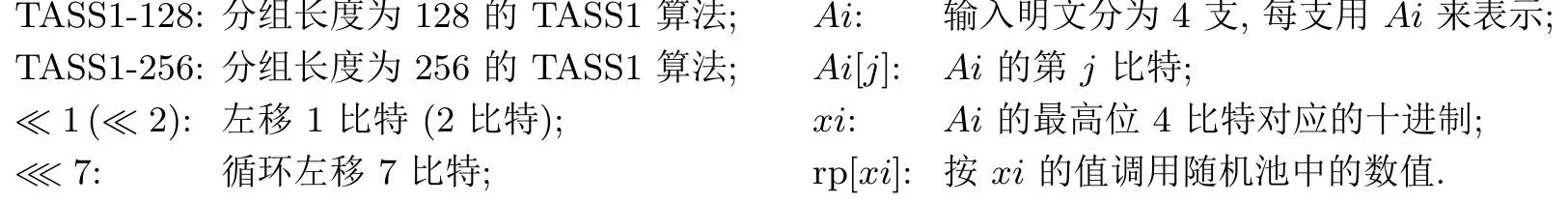
2.2 算法描述

2.2.1 TASS1 算法加密过程

首先, 介绍TASS1 算法的特殊之处在于使用密化随机池来代替S 盒实现非线性的功能. 算法中使用的是由16 个存储单元构成的随机池, 随机池的初始值如表1.

表1 随机池的初始值Table 1 Initial value of random pool

随机池的初始值可以作为秘密在一个用户群中共享, 在进行加密时, 经过密钥作用下的一系列变换,随机池被加密成秘密数值, 将其称之为密化随机池. 加解密过程中调用的是密化随机池中的值. TASS1 算法采用广义的Feistel 结构, 轮函数采用非线性移位寄存器递归方法, 加密流程如图1 所示.

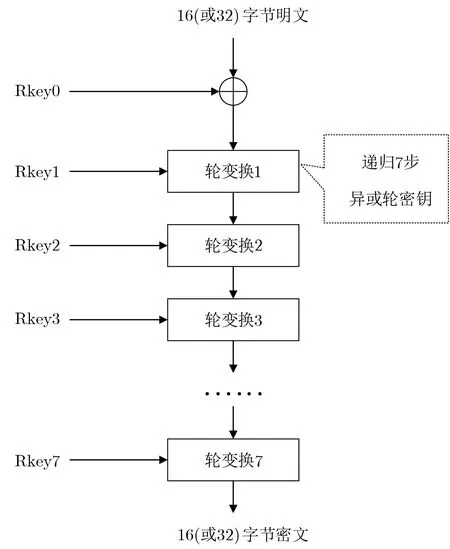
图1 TASS1 加密过程Figure 1 TASS1 encryption

TASS1 的轮函数为7 步递归结构, 由异或、≪1、≪2、≪7、异或随机池等操作组成. 非线性移位寄存器递归方法如下:

(1) 将输入的16 字节(或32 字节) 按32 位字(或64 位字) 存入A0,A1,A2,A3.

(2) 将A3 的最高位4 比特取出, 记作x3, 计算A=(A3≪1)⊕rp[x3], 并将A异或到A2 中.

(3) 将新A2 的最高位4 比特取出, 记作x2, 计算A=(A2≪2)⊕rp[x2], 并将A异或到A1 中.

(4) 对新产生的A1 和A2, 计算A4=A0⊕A1⊕A2⊕A3.

(5) 令Y=A1⊕A2, 将Y的最高位4 比特取出, 记作x12, 计算A=(Y≪7)⊕rp[x12], 并将A异或到A3 中.

至此, 完成了一步递归, 产生了A4, 并变换了A1,A2,A3. 同样地, 由A4 和其高位4 比特值x4, 计算A=(A4≪1)⊕rp[x4],将A异或到A3; 由新A3 及高位4 比特值x3 计算A=(A3≪2)⊕rp[x3],将A异或到A2; 使用新的A2,A3,计算A5=A1⊕A2⊕A3⊕A4. 同样地, 由A2⊕A3 改造A4. 这样, 又完成了一步递归,产生了A5,并变换了A2,A3,A4,···,重复这种递归,直到计算出A10=A6⊕A7⊕A8⊕A9,并使A7,A8,A9 发生了变换. 最后, (A7,A8,A9,A10) 作为非线性移位寄存器7 步递归的输出结果.

TASS1 算法的一步递归过程如图2 所示.

图2 TASS1 的一步递归Figure 2 1-step recursion of TASS1

2.2.2 TASS1 算法密钥生成算法

密钥生成包括密钥填充和密钥初始化两部分. 密钥初始化的内容包括生成轮密钥和加密随机池. 当分组长度为128 比特时, 若用户密钥不足32 字节, 则需按照密钥填充规则将其扩展至32 字节, 然后作密钥初始化. 当分组长度为256 比特时, 若用户密钥不足64 字节, 则需要将其填充至64 字节.

(1) 密钥填充

当分组长度为128 比特时, 若所用密钥少于32 字节, 设密钥长为n字节, 14≤n ＜32, 记密钥为K0,K1,··· ,K(n −1), 则对i=n,n+1,··· ,31, 约定Ki=i+K(i −n)mod 256. 例如, 用户的20 字节密钥为“0x64, 0x83, 0x02,···, 0xa6”, 则第21 字节密钥K20 = 20+0x64 = 0x78,第22 字节K21=21+0x83=0x98.分组长度为256 比特时, 若所用密钥少于64 字节, 则需要将其填充到64 字节. 将n字节密钥记作K0,K1,··· ,K(n −1), 16≤n ＜64, 则对i=n,n+1,··· ,63, 约定Ki=i+K(i −n)mod 256.

(2) 密钥初始化

密钥初始化的基本过程如下:

(a) 由完成填充后的密钥与随机池共同简单地生成8 个初级轮密钥.

(b) 四次调用加密函数将随机池加密, 生成密化随机池.

(d) 由密化密钥和密化随机池组合出4 个轮密钥, 明确8 个实用轮密钥.

3 TASS1-128 的40 步不可能差分区分器

TASS1 算法的主要非线性部件在于查询密化随机池, 且密化随机池是根据密钥而定的, 故密码性能指标未知. 根据加密函数可知真正对随机池中的值起影响作用的是Ai的最高4 位.

3.1 概率为1 的19 步差分特征

差分特征的搜索思路如下: 对于输入差分, 使其尽可能晚地到达高4 位, 从而使得该差分扩散速度相对较慢. 对于TASS1-128, 将4 个32 位输入从高到低分别记为A3,A2,A1,A0. 在A3[2,3,6,9] 注入差分为1,A2[0,2,5,8,10] 注入差分为1,A1[1,5,6,7,10] 注入差分为1,A0[1,5,6,7,10] 注入差分为1. 通过算法1 可以正向推导8 步概率为1 的差分路径,通过算法2 可以反向推导5 步概率为1 的差分路径.

算法1: TASS1 算法差分注入正向推导Input: 4 个32 bit 的二进制数A3,A2,A1,A0 Output: 4 个32 bit 的二进制数C3,C2,C1,C0 1 while 1 do Break;5 end 6 C2 ≪2 ⊕A1 →C1 7 A0 ⊕C1 ⊕C2 ⊕A3 →C0 8 if C1 ⊕C2 的高四位是0 then 2 A3 ≪1 ⊕A2 →C2 3 if C2 的高四位是0 then 4 Break;10 end 11 (C1 ⊕C2) ≪7 ⊕A3 →C3 12 将C3,C2,C1,C0 互换至C2,C1,C0,C3 13 end 9算法2: TASS1 算法差分注入反向推导Input: 4 个32 bit 的二进制数A3,A2,A1,A0 Output: 4 个32 bit 的二进制数C3,C2,C1,C0 1 while 1 do Break;4 end 5 (A1 ⊕A0) ≪7 ⊕A2 →C3 6 if C3 的高四位是0 then 2 if A1 ⊕A0 的高四位是0 then 3 Break;8 end 9 C3 ≪1 ⊕A1 →C2 10 if A1 的高四位是0 then 7 11 Break;12 end 13 A1 ≪2 ⊕A3 →C1 14 C3 ⊕A0 ⊕A1 ⊕A3 →C0 15 end

根据以上算法的推导, 可以得到13 步概率为1 的差分路径, 具体差分路径如表2 所示.

图2 中概率为1 的差分路径是根据输入差分特征进行搜索得到, 不具备普适性, 因为这种差分特征相邻轮数之间线性关系明显, 所以可以通过构建齐次线性方程组进行推导.

由于TASS1 算法的轮函数大部分采用了线性结构,相邻轮数的数据之间容易构建齐次线性方程组,由方程组得到系数矩阵, 根据系数矩阵的秩和自由变量个数的比较, 可以确定该方程组是否有解. 将TASS1的输入按位确定变量, 128 位输入即存在128 个变量, 128 位输出即存在另外128 个变量,所以一步涉及到256 个变量. 每一步的输出可作为下一步的输入,所以假设当前步数为x,则涉及的变量数为128×(x+1).

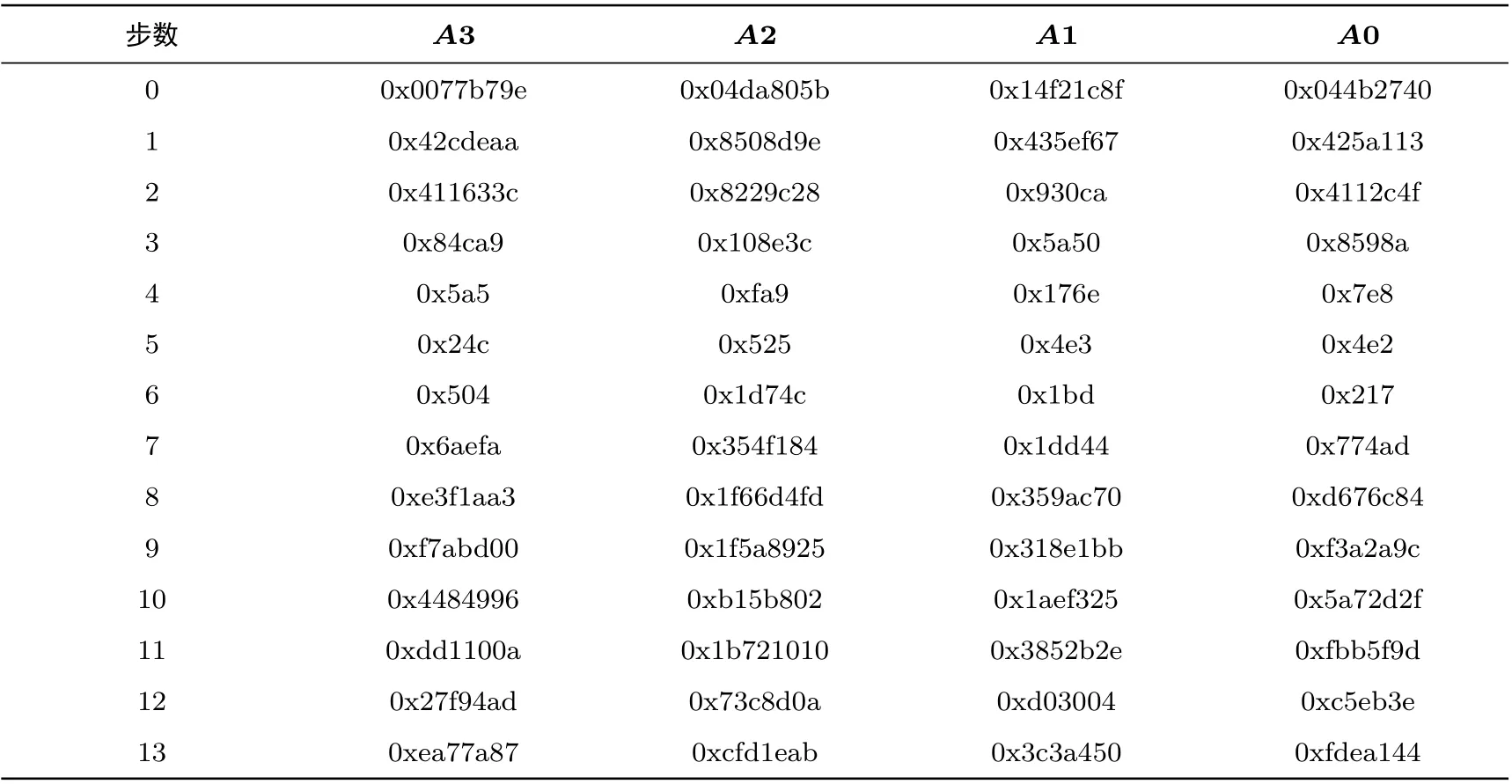
表2 TASS1-128 的13 步差分路径Table 2 13-step differential path of TASS1-128

已知TASS1 算法的主要非线性部件是密化随机池, 影响该随机池的值为该输入的最高4 比特. 考虑输入差分时只需保证该输入的最高4 比特为0, 即可使得差分传递线性化, 由此可构造限制条件方程.

构建TASS1-128 的具体方程组如表3 所示, 其中x0,x1,··· ,x126,x127为128 位输入,y0,y1,···,y126,y127为图2 所示未进行分支循环操作前的128 位输出.

表3 TASS1-128 差分特征方程组Table 3 Differential characteristic equations of TASS1-128

对于19 步TASS1-128 得到规模为2660×2560 的系数矩阵, 调用python 的numpy 库对该系数矩阵进行求解, 得到秩为2558. 因为系数矩阵的秩小于变量数, 即2558＜2660, 所以该方程组存在非零解,且有3 个非零解. 考虑求解线性方程组, 利用高斯消元法的时间复杂度为O(n3), 给出求解该线性方程组的时间复杂度＜O(236).

当递归步数增加时(＞19 步), 得到的秩始终等于变量个数, 即对应齐次线性方程组只有零解. 所以TASS1-128 算法至少存在3 条概率为1 的19 步差分路径.

3.2 40 步不可能差分区分器

因为0x10CA3066̸= 0x00E61085, 概率为0, 故可构造的不可能差分路径为28 步. 不可能差分的路径示意图如图3 所示.

图3 TASS1-128 的28 步不可能差分路径Figure 3 28-step impossible differential path of TASS1-128

其中A3,A2,A1,A0 字长为n, 则由此路径可以构造2r+2 步不可能差分区分器.

首先, 将(1)式方程作为限制条件加入表3 的方程组进行系数矩阵求秩, 得到方程组的秩与原方程组的秩相同, 故19 步差分路径满足该条件.

其次, 将(2)式的不等式改为等式, 约定xj(i)为第j步差分路径的第i位, 将等式换算成方程组得:

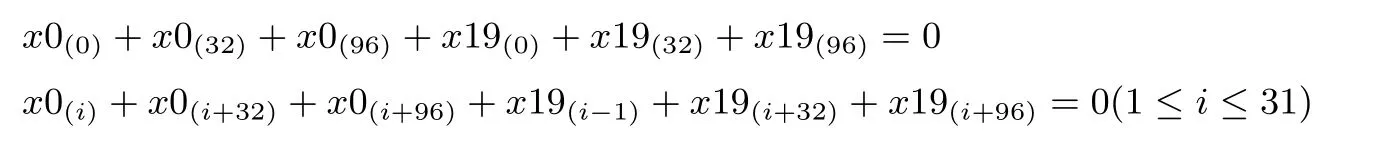
将上述方程作为限制条件加入表3 的方程组进行系数矩阵求秩, 得到秩等于变量数, 即齐次线性方程组没有非零解. 故该等式不成立, 即(2)式成立.

综上所述, 每条概率为1 的19 步差分路径均可以构造40 步不可能差分区分器.

TASS1-128 共有49 步, 目前由3 条概率为1 的19 步差分路径可组合构造r(3≤r ≤8) 条40 步不可能差分路径.

4 TASS1-256 的82 步不可能差分区分器

TASS1-256 与TASS1-128 的非线性部件同样采用高4 位查询随机池的方式. 根据递归算法可知TASS1-128 中只有12 比特起到非线性作用, 而当分组长度由128 比特增加到256 比特时, TASS1-256 中也只有12 比特起到非线性作用, 因此更容易利用差分特征对该算法进行分析.

在此基础上, 我们认为TASS1-256 的安全性较TASS1-128 的安全性更差一些, 最后的分析结果显示确实如此.

4.1 概率为1 的40 步差分特征

TASS1-256 与TASS1-128 大致相同, 不同点主要表现为输入的分组长度. 求差分路径的时, 仅需改变算法1 和算法2 的输入和输出二进制长度即可. 将4 个64 位输入从高到低分别记为A3,A2,A1,A0.在A3[0,1,4,9,10] 注入差分为1,A2[1,2,4,7,10,11] 注入差分为1,A1[0,1,5,6,9] 注入差分为1,A0[0,1,5,6,9] 注入差分为1. 通过改变输入的算法1 可以正向推导7 步概率为1 的差分路径, 通过改变输入的算法2 可以反向推导14 步概率为1 的差分路径. 故可得到21 步差分路径, 具体路径如表4所示. TASS1-256 一步输入输出涉及到512 个变量, 所以x步涉及的变量总数为256×(x+1) 个. 构建TASS1-256 的具体方程组如表5 所示, 其中x0,x1,··· ,x254,x255为256 位输入, 为图2 所示未进行分支循环操作的256 位输出.

显然, 这个方程组的系数矩阵更加稀疏, 根据以上方程可以得到40 步的规模为10720×10496 的系数矩阵, 调用python 中的numpy 库对该系数矩阵进行求解, 得到秩为10490. 因为系数矩阵的秩小于变量数, 即10490＜10496, 可得该方程存在非零解, 且有63 个解. 所以TASS1-256 存在63 条概率为1 的40 步差分路径. 考虑求解线性方程组, 利用高斯消元法的时间复杂度为O(n3), 给出求解该线性方程组的时间复杂度＜O(242).

4.2 82 步不可能差分区分器

根据实验搜索可以得到具体TASS1-256 的21 步差分路径, 再由不可能差分构造思想容易构造44 步不可能差分路径.

根据方程组的系数矩阵秩求解, 证明存在40 步概率为1 的差分路径, 结合不可能差分区分器构造条件(推论1), 可以构造82 步不可能差分区分器.

首先, 针对TASS1-256 对推论1 中的(1)式进行变换得到,

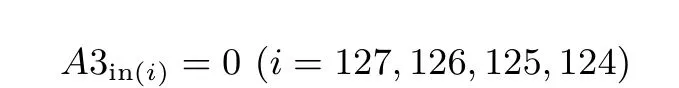
其中A3in表示第4 支(从低位到高位) 的输入差分, 将上述方程作为限制条件加入表5 的方程组中进行系数矩阵求秩, 得到方程组的秩与原方程组的秩相同, 故可知40 步差分路径满足推论1 的第一个条件.

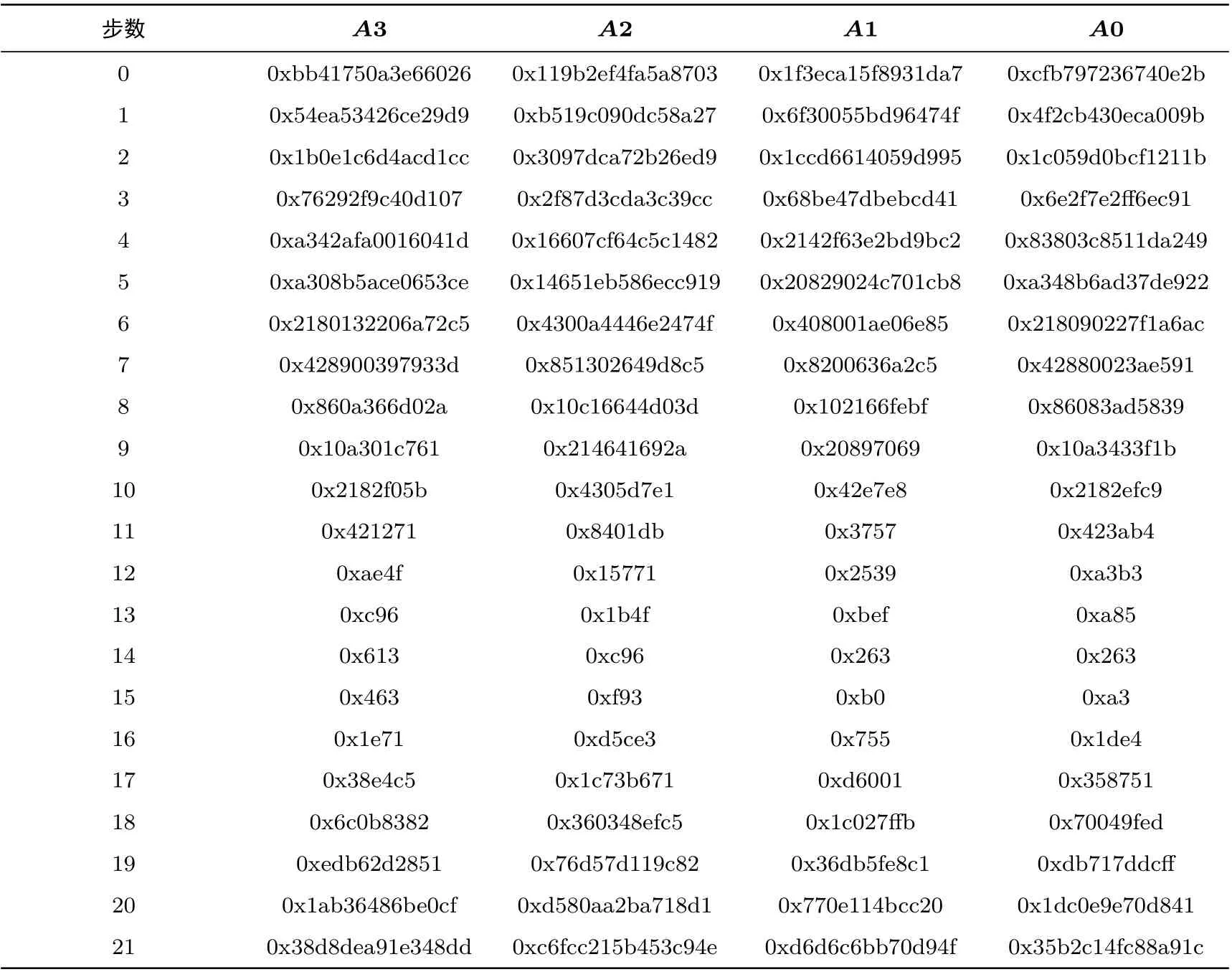
表4 TASS1-256 的21 步差分路径Table 4 21-step differential path of TASS1-256

表5 TASS1-256 差分特征方程组Table 5 Differential characteristic equations of TASS1-256

其次, 将推论1 中的(2)对应的不等式改为等式, 约定xj(i)为第j步差分路径的第i位, 将等式换算成方程组得:

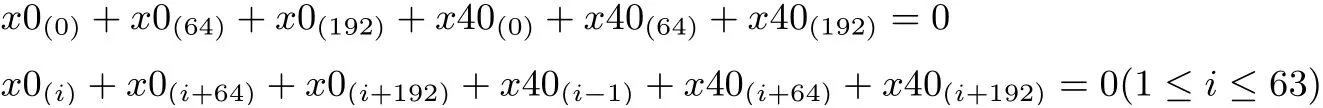
将上述方程作为限制条件加入表5 的线性方程组进行系数矩阵求秩, 得到秩等于变量数, 即齐次线性方程组没有非零解. 故该等式不成立, 即(2)式成立.

综上所述, 可知每条概率为1 的40 步差分路径均满足推论1, 即每条概率为1 的40 步差分路径均可以构造82 步不可能差分区分器. TASS1-256 的总步数为49 步, 已知存在82 步的不可能差分区分器, 这比它本身存在的49 步要更多, 所以可以证明TASS1-256 算法无法对抗不可能差分攻击, 该算法不安全.

5 结论

本文评估了分组密码算法TASS1 抵抗差分和不可能差分的安全性. 当算法分组长度为128 比特时,通过对相邻轮的状态比特构造线性方程组, 测试系数矩阵的秩小于自变量个数, 推得方程组存在非零解,从而理论证明可得到19 步概率为1 的差分路径, 由此路径可以构造40 步不可能差分路径; 而当分组长度为256 比特时, 构造类似的线性方程组并求秩, 理论证明可得到40 步概率为1 的差分路径, 由此路径可以构造82 步(全轮为49 步) 不可能差分路径. TASS1 分组密码算法迭代一共为49 步, 根据以上分析结果, 可以得到TASS1 算法无论是128 比特还是256 比特版本的安全性都是不够的.

表6 TASS1 算法分析结果Table 6 Analysis results for TASS1

对于TASS1 算法的改进意见, 建议在算法的两个部件进行完善: 首先, 对随机池密化环节进行简化,使其密码指标更加清晰明了, 这样设计者对算法的安全性评估会更准确; 其次, 对轮函数进行改进, 修改非线性部件的设计, 加大参与非线性混乱的比特量, 使得较短轮数内数据的混乱更加充分, 由此加强算法抵抗高概率差分分析的能力.