循环移位与异或构造扩散层的新证明方法*

苏 俊, 王 鑫, 王 涛, 杨 波

陕西师范大学 计算机科学学院, 西安710119

1 引言

扩散层作为分组密码和哈希函数的核心组件, 其目的是提高扩散和混淆程度来实现雪崩效应[1], 这有助于抵抗差分分析、线性分析以及一些未知分析方法的攻击. 通常使用分支数这一概念作为评价扩散层安全性能的指标[2]. 具体体现为分支数较大, 则该密码系统的扩散性能较优, 抵抗差分攻击与线性攻击的能力更强. 随着轻量级密码学的快速发展, 利用软硬件设备设计高效的扩散层逐渐成为研究热点[3,4].

从编码理论的角度看, 采用最大距离可分(Maximum Distance Separable, MDS) 码构造扩散层可使分支数达到最大[5], 然而由于有限域中乘法的存在, 导致传统MDS 不适用于RFID 系统和传感器网络等资源受限的环境. 为了解决这一问题, PHOTON 轻量级Hash 函数族的设计者们[6]采用流密码算法中的LFSR 设计思想通过递归构建扩散层置换[7], 其首先实现一个线性反馈寄存器的循环函数, 然后运行几轮函数之后得到一个MDS 矩阵, 此方法能较好的节省硬件空间, 但该方法需要迭代多次, 导致方法效率低,不适用于低时延的环境[8]; 采用直接方法构造轻量级MDS 矩阵可以提高算法效率, 但其只关注硬件实现,而未考虑到软件性能[9]; Philip 等人提出采用循环结构来构建轻量级MDS 矩阵[10], 其所得的循环矩阵中所有矩阵块结构相同, 因此可以通过重复使用乘法电路来节省硬件面积. 因此, 在扩散层中使用循环矩阵可以在硬件面积和时钟周期之间进行权衡[11,12].

循环移位和异或运算的线性变换与循环矩阵一一对应[13], 所以利用循环移位和异或运算来构建扩散层的方法具有循环矩阵同样的优势, 且其确定线性变换相对应矩阵的第一行后, 经过循环就能确定整个循环矩阵, 因此也称此结构为逐位循环[14]. 采用循环移位和异或运算构造最优线性变换[15], 不仅运算效率高、软硬件实现简单, 同时还避免了条件分支语句和查表运算导致算法容易被攻击的缺点[16]. 文献[14]中对扩散层的最优线性变换转换成循环矩阵, 再判断其子矩阵全部是非奇异矩阵来证明该扩散层具有最大分支数[17]. 但是上述方法仅能够证明最优扩散层中的分支数大小, 无法判断非最优扩散层中分支数的大小.

为了解决上述问题,在本文中,我们提出了一种反证的方法,利用扩散层中输入与输出的关系证明分支数的大小. 这种方法不仅在证明方式上更直接, 而且不再局限于最优线性变换. 我们对输入形式为(Fn2)m的最优线性变换利用上述方法进行了详细证明, 最后, 给出了扩散层中线性变换的一种筛选算法和(Fn2)m上最优与次优线性变换组合, 以及分析筛选结果后得到两个结论.

2 基本概念

2.1 分支数

W(P(X)) 表示扩散层中输出数据的汉明重量, 当B(P)=m+1 时, 扩散层的分支数达到最大, 被称为最优线性变换[12]; 当B(P)=m时, 称为次优线性变换, 它能够用更少的移位和异或运算来实现, 所以更具有轻量化, 并且在多轮迭代后能够有最好扩散效果, 因此研究次优线性变换也有一定的现实意义[20].

2.2 一般形式与必要条件

3 一类最优线性变换的证明

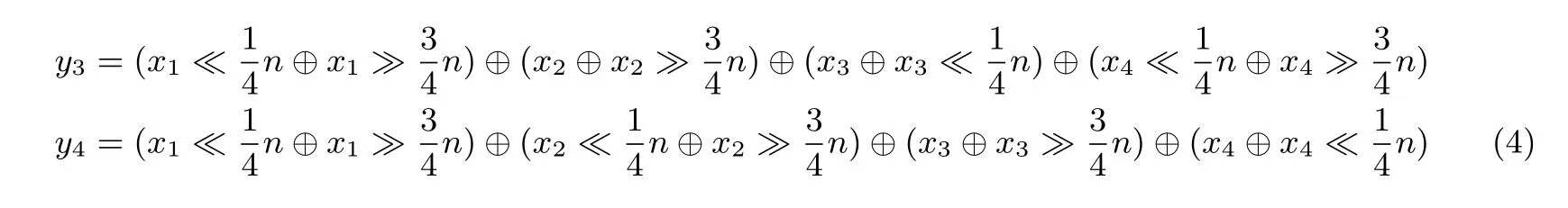
下面分别讨论x1,x2,x3,x4中任意不为0 情况下X和Y的汉明重量之和, 也就是X的汉明重量为分别为1, 2, 3 和4 时上述线性变换的分支数. 从等式中可以看到y1,y2,y3,y4的形式相似, 所以分类讨论时, 从x1,x2,x3,x4中任意选取xi不为0 后会得到相似形式的y1,y2,y3,y4, 所以不同xi的选取对证明过程不会产生影响.

3.1 X 中汉明重量为1

当X中汉明重量为1 时, 也就是x1,x2,x3,x4中仅存在一个不为0 的情况, 不失一般性, 设x1̸=0,x2,x3,x4=0, 此时有

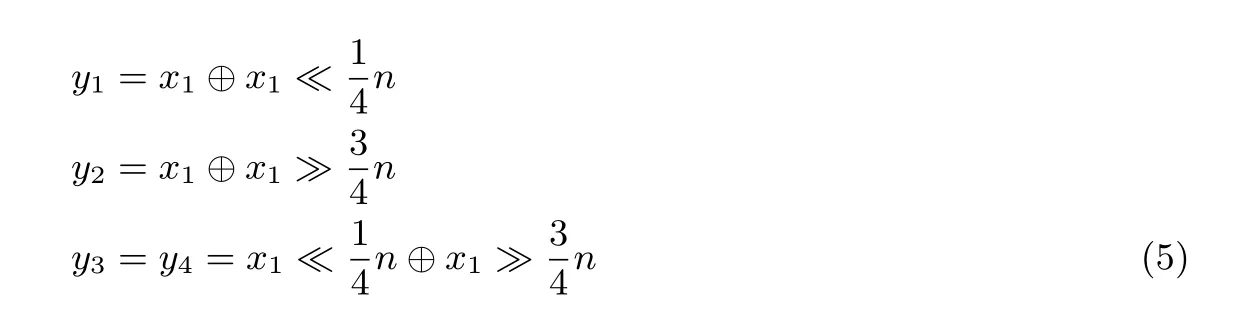
假设y1,y2,y3,y4中至少存在一个为0, 那么分别讨论y1,y2,y3,y4等于0 的情况:

(1) 当y1= 0 时, 按块展开得等式x11⊕x12= 0,x12⊕x13= 0,x13⊕x14= 0, 那么x14= 0, 则有x1=0, 这与条件相矛盾, 所以y1̸=0.

(2) 当y2= 0 时, 按块展开得等式x11= 0,x12= 0,x13= 0,x14⊕x11= 0 则有x1= 0, 这与条件相矛盾, 所以y2̸=0.

(3) 当y3=y4=0 时, 按块展开得等式x11=0,x12=0,x13=0,x14=0 则有x1=0, 这与条件相矛盾, 所以y3=y4=0.

综上所述, 当x1̸=0 时,y1,y2,y3,y4均不为0, 所以X和Y的汉明重量之和为5.

3.2 X 中汉明重量为2

当X中汉明重量为2 时, 讨论x1,x2,x3,x4中存在两个不为0 的情况, 不失一般性, 设x1,x2̸=0, x3,x4=0, 此时有

此种情况可以分为两类x1=x2和x1̸=x2讨论:

(1) 当x1=x2时, 会有

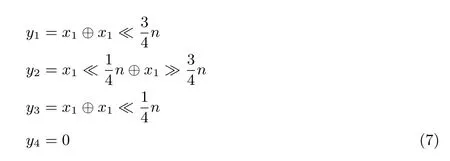
由上推理可得x2= 0, 这与条件x2̸= 0 相矛盾, 所以当y2= 0 时,y1=y2̸= 0; 综上所述当x1,x2̸=0 时,y1,y2,y3,y4至少存在三个不为0, 所以在该种情况下X和Y的汉明重量之和至少为5.

3.3 X 中汉明重量为3

当X中汉明重量为3 时, 讨论x1,x2,x3,x4存在三个不为0 的情况, 设x1,x2,x3̸=0,x4=0, 此时有

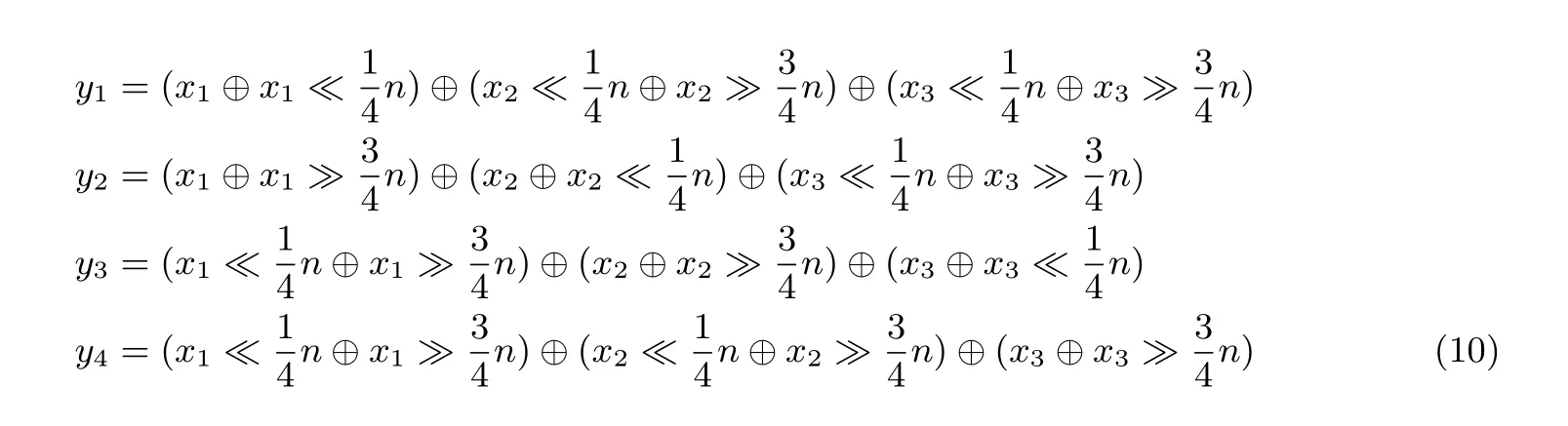
仅需要证明y1,y2,y3,y4中至少存在两个不为0, 就可以判断X和Y的汉明重量之和不小于5; 利用反证法, 假设y1,y2,y3,y4至少存在三个为0, 由于

可以将这种情况分为两类: (1)y1=y4=0 的情况下, 判断y2和y3是否等于0; (2)y2=y3=0 的情况下, 判断y1和y4是否等于0. 下面进行讨论:

3.4 X 中汉明重量为4

当X中汉明重量为4 时, 讨论x1,x2,x3,x4全部不为0 的情况, 设x1,x2,x3,x4̸= 0, 此时仅需要证明y1,y2,y3,y4中至少存在一个不为0, 可证得X和Y的汉明重量之和不小于5. 利用反证法, 设y1,y2,y3,y4=0, 则有

4 循环移位与异或扩散层的筛选

一般筛选特定分支数的线性变换总是依赖于程序的遍历, 因此确定一个较小的空间可极大地节约遍历时间并提高搜索特定线性变换的概率. 本节根据定理1 和定理2 给出一个筛选特定分支的线性变换算法,即直接对输入数据进行运算后进行分支数大小的筛选. 算法的输入为循环移位项数和指定分支数, 输出为线性变换组合. 算法对移位项数为n的线性变换组合进行筛选, 首先遍历该移位项数下的所有线性变换组合, 其中, 在每种线性组合中遍历混淆层输出数据, 然后计算输入与输出的汉明重量, 如果汉明重量小于分支数Branch 则中断X遍历, 开始进行下一种线性组合筛选. 本节以筛选X ∈(F82)4上最简形式的最优线性变换为例, 其核心算法如下:

算法1 筛选特定分支数的线性变换组合Input: 移位项数r = 5; 分支数Branch = 5 Output: 移位数l1,l2,l3,l4,l5 1 for l1 from 0 to 6 do 4 for l5 from l1 +1 to 7 do 2 ···;3 for l4 from 24 to 31 do 5 for X from 1 to 232 −1 do 6//扩散层中输入数据进行线性变化7 Y = [X ≪l1|X ≫(32−l1)]∧[X ≪l2|X ≫(32−l2)]∧···∧[X ≪l5|X ≫(32−l5)]8//计算输入与输出的汉明重量之和Weight = [(X & 0xf0000000)]+···+[[(X & 0x0000000f)]]+[[(Y &0xf0000000)]]+···+[[(Y & 0x0000000f)]]10 if Weight ＜Branch then then 9 11 go to Step4;12 else 13 save l1,l2,l3,l4,l5 to text;//筛选成功, 结果存入文件14 end 15 end 16 end 17 end 18 end

4.1 ()4 上最优线性变换

表1 ()4 上的分支数为5 的扩散层Table 1 Diffusion layer with 5 branches on ( )4

表1 ()4 上的分支数为5 的扩散层Table 1 Diffusion layer with 5 branches on ( )4

n r (Fn2 )4 中的l1,l2,···,lr 4 5 {0, 1, 5, 9, 12}{0, 3, 7, 11, 12}{0, 4, 5, 9, 13}{0, 4, 7, 11, 13}{1, 4, 8, 9, 13}{1, 5, 8, 12, 13}{3, 4, 8,11, 15}{3, 7, 8, 12, 15}4 7 {0, 1, 4, 6, 8, 11, 12}{0, 2, 4, 7, 8, 12, 13}{0, 3, 4, 8, 9, 12, 14}{0, 4, 5, 8, 10, 12, 15}8 5 {0, 2, 10, 18, 24}{0, 6, 14, 22, 24}{0, 8, 10, 18, 26}{0, 8, 14, 22, 26}{2, 8, 16.18, 26}{2, 10, 16, 24,26}{6, 8, 16, 22, 20}{6, 14, 16, 24, 30}8 7 {0, 2, 8, 12, 16, 22, 24}{0, 4, 5, 13, 17, 22}{0, 4, 8, 14, 16, 24, 26}{0, 4, 9, 11, 19, 24, 29}{0, 6, 8, 16,18, 24, 28}{0, 6, 10, 15, 19, 27, 28}{0, 8, 10, 16, 20, 24, 30}{1, 3, 11, 16, 21, 24, 28}{1, 5, 9, 12, 17, 19,27}{1, 6, 10, 16, 20, 21, 29}{2, 6, 12, 13, 20, 27, 28}{2, 7, 11, 19, 20, 24, 30}{2, 8, 12, 13, 21, 25,30}{3, 4, 8, 14, 18, 23, 27}{3, 4, 10, 14, 20, 21, 28}{3, 7, 13, 21, 23, 28, 31}{3, 9, 13, 16, 20, 25, 27}{3,11, 12, 16, 22, 26, 31}{4, 5, 12, 19, 20, 26, 30}{4, 7, 11, 15, 21, 29, 31}{4, 11, 12, 18, 22, 28, 29}{5, 7,12, 15, 19, 23, 29}{5, 9, 14, 18, 24, 28, 29}{5, 13, 25, 20, 23, 27, 31}

分析表1 的线性组合不难看出, 在循环移位与异或运算最优扩散层中, 当X ∈(Fin2)m时, 分支数不会发生改变, 因此有如下推论:

表2 ()4 中最优扩散层的最简形式Table 2 Simplest form of optimal diffusion layer on ()4

表2 ()4 中最优扩散层的最简形式Table 2 Simplest form of optimal diffusion layer on ()4

最优线性变换 (Fn2 )4 中的l1,l2,l3,l4,l5 (Fn 2 )4 中的l1,l2,l3,l4,l5第一组 0,1,5,9,12 0, 1 4 n,n+ 1 4 n,2n+ 1 4 n,3n第二组[14] 0,3,7,11,12 0, 3 4 n,n+ 3 4 n,3n第三组 0,4,5,9,13 0,n,n+ 1 4 n,2n+ 3 4 n第四组[21] 0,4,7,11,15 0,n,n+ 3 4 n,2n+ 1 4 n,3n+ 1 4 n第五组 1,4,8,9,13 1 4 n,2n+ 3 4 n,3n+ 3 4 n,n,2n,2n+ 1 4 n第六组 1,5,8,12,13 1 4 n,3n+ 1 4 n,n+ 1 4 n第七组 3,4,8,11,15 3 4 n,2n,3n,3n+ 1 4 n,n,2n,2n+ 3 4 n第八组 3,7,8,12,15 3 4 n,3n+ 3 4 n,n+ 3 4 n,2n,3n,3n+ 3 4 n

4.2 ()4 上次优线性变换

表3 ()4 上分支数为4 的次优扩散层Table 3 Suboptimal diffusion layer with branch number of 4 on ()4

表3 ()4 上分支数为4 的次优扩散层Table 3 Suboptimal diffusion layer with branch number of 4 on ()4

n r (Fn 2 )4 中的l1,l2,···,lr 4 3 {0, 4, 8}{0, 4, 12}{0, 8, 12}{4, 8, 12}4 5 {0, 1, 4, 8, 9}{0, 1, 4, 9, 12}{0, 1, 8, 9, 12}{0, 1, 5, 9, 13}{0, 2, 4, 8, 10}{0, 2, 4, 10, 12}{0, 2, 6, 10,14}{0, 2, 8, 10, 12}{0, 3, 4, 8, 11}{0, 3, 4, 11, 12}{0, 3, 5, 11, 13}{0, 3, 7, 11, 15}{0, 3, 8, 11, 12}{0, 4,5, 8, 12}{0, 4, 5, 12, 13}{0, 4, 6, 8, 14}{0, 4, 6, 12, 14}{0, 4, 7, 8, 15}{0, 4, 7, 12, 15}{0, 5, 8, 12,13}{0, 6, 8, 12, 14}{0, 7, 8, 12, 15}{1, 4, 5, 9, 13}{1, 4, 7, 9, 15}{1, 4, 8, 9, 12}{1, 5, 8, 9, 13}{1, 5, 9,12, 13}{1, 7, 9, 12, 15}{2, 4, 6, 10, 14}{2, 4, 8, 10, 12}{2, 6, 8, 10, 14}{2, 6, 10, 12, 14}{3, 4, 8, 11,12}{3, 5, 8, 11, 13}{3, 7, 8, 11, 15}{3, 7, 11, 12, 15}{4, 5, 8, 12, 13}{4, 6, 8, 12, 14}{4, 7, 8, 12, 15}8 3 {0, 8, 16}{0, 8, 24}{0, 16, 24}{8, 16, 24}8 5 {0, 1, 8, 16, 17}{0, 1, 8, 17, 24}{0, 1, 9, 17, 25}{0, 1, 16, 17, 24}{0, 2, 8, 16, 18}{0, 2, 8, 18, 24}{0, 2,10, 18, 26}{0, 2, 16, 18, 24}{0, 3, 8, 16, 19}{0, 3, 8, 19, 24}{0, 3, 11, 19, 27}{0, 3, 16, 19, 24}{0, 4, 8,16, 20}{0, 4, 8, 20, 24}{0, 4, 12, 20, 28}{0, 4, 16, 20, 24}{0, 5, 8, 16, 21}{0, 5, 8, 21, 24}{0, 5, 9, 21,25}{0, 5, 13, 21, 29}{0, 5, 16, 21, 24}{0, 6, 8, 22, 24}{0, 6, 10, 22, 26}{0, 6, 14, 22, 30}{0, 6, 15, 22,24}{0, 7, 8, 16, 23}{0, 7, 8, 23, 24}{0, 7, 9, 23, 25}{0, 7, 11, 23, 27}{0, 7, 15, 23, 31}{0, 7, 16, 23,24}{0, 8, 9, 16, 25}{0, 8, 9, 24, 25}{0, 8, 9, 24, 26}{0, 8, 10, 16, 26}{0, 8, 11, 16, 27}{0, 8, 11, 24,27}{0, 8, 12, 16, 28}{0, 8, 12, 24, 28}{0, 8, 13, 16, 29}{0, 8, 13, 24, 29}{0, 8, 14, 16, 30}{0, 8, 14, 23,30}{0, 8, 15, 16, 31}{0, 8, 15, 24, 31}{0, 9, 16, 24, 25}{0, 10, 16, 24, 26}{0, 11, 16, 24, 25}{0, 12, 16,24, 28}{0, 13, 16, 24, 29}{0, 14, 16, 24, 30}{0, 15, 16, 24, 31}{1, 8, 9, 17, 25}{1, 8, 13, 17, 29}{1, 8,15, 17, 31}{1, 8, 16, 17, 24}{1, 9, 16, 17, 25}{1, 9, 17, 24, 25}{1, 13, 17, 24, 29}{1, 15, 17, 24, 31}{2,8, 10, 18, 26}{2, 8, 14, 18, 30}{2, 8, 16, 19, 18, 24}{2, 10, 16, 18, 26}{2, 10, 18, 24, 26}{2, 14, 18, 24,30}{3, 8, 11, 19, 27}{3, 8, 15, 19, 31}{3, 8, 16, 17, 24}{3, 11, 16, 19, 27}{3, 11, 19, 24, 27}{3, 15, 19,24, 31}{4, 8, 12, 20, 28}{4, 8, 16, 20, 24}{4, 12, 16, 20, 28}{4, 12, 20, 24, 28}{5, 8, 13, 21, 29}{5, 8,16, 21, 24}{5, 9, 16, 21, 25}{5, 13, 16, 21, 29}{5, 13, 21, 24, 29}{6, 8, 14, 22, 30}{6, 8, 16, 22, 24}{6,10, 16, 22, 26}{6, 14, 16, 22, 30}{6, 14, 22, 24, 30}{6, 8, 16, 22, 31}{7, 8, 15, 23, 31}{7, 8, 16, 23,24}{7, 9, 16, 23, 25}{7, 11, 16, 23, 27}{7, 14, 16, 24, 30}{7, 15, 16, 23, 31}{7, 15, 23, 24, 31}{8, 9, 16,24, 25}{8, 10, 16, 24, 26}{8, 11, 16, 24, 27}{8, 12, 16, 24, 28}{8, 13, 16, 24, 29}{8, 15, 16, 24, 31}

通过分析表3 中次优线性组合, 我们发现在循环移位与异或运算构造的非最优线性变换有如下结论:

推论2 如果线性变换L(X,m,n) 是分支数为B的非最优线性变换, 那么该线性变换满足下列条件:移位项数r为奇数且r+1≥B,移位数l至少从B−1 个不同区间[ni,n(i+1)]内取值,i=0,1,··· ,m−1.

假设在分支数为B的线性变换L(X,m,n) 中,r+1＜B, 经线性变换后知Y中最多r项包含x1的最低位信息, 换句话说x1的最低位参与生成Y中最多r项yi的异或运算, 在该情形下, 若X中仅有x1的最低位为1, 也就是X=1 时, 输出Y中最多r项yi非零, 那么其汉明重量最大为r, 所以线性变换的分支数为r+1, 此时r+1＜B与分支数为B条件矛盾, 所以在分支数为B的线性变换L(X,m,n) 中,r+1≥B, 并且由定理2 中公式(4) 得知, 要想x1的最低位参与Y中r项y的生成, 移位数l至少从B −1 个[ni,n(i+1)] 区间取值, 其中i=0,1,··· ,m −1.

5 结论