SM4 算法快速软件实现*
2021-01-13张笑从张习勇刘建伟
张笑从, 郭 华, 张习勇, 王 闯, 刘建伟
1. 北京航空航天大学 软件开发环境国家重点实验室, 北京100191
2. 密码科学技术国家重点实验室, 北京100878
3. 北京航空航天大学 空天网络安全工业与信息化部重点实验室, 北京100191
4. 北京卫星信息工程研究所, 北京100086
1 引言
SM4 分组密码算法[1]是我国自主设计的对称分组密码, 为众多信息系统提供安全、完整的数据加密方案. SM4 算法的高效软件实现为我国应用在安全产品(如IPSec、VPN、SSL、TLS 等)上的密码算法由国际标准替换为国家标准提供了强有力的支撑, 为SM4 算法广泛用于政府办公、公安、银行、税务、电力等自主可控要求高的信息系统提供了可靠的保障. 目前关于SM4 算法的软件优化实现方面的相关工作不多, 多使用查表的方法[2], 但由于代替表规模相对较大, CPU 在做查表操作时, 表中数据在内存和cache之间频繁对换导致查表延时较大, 且不利于高效并行加/解密多组消息. 此外, 查表法无法抵抗缓存-计时侧信道攻击, 因此在一定程度上制约了SM4 的软件实现性能和安全性.
1996 年Intel 推出单指令多数据的SSE (Streaming SIMD Extensions) 指令集后, Biham[3]于1997年提出一种新的对称分组密码快速软件实现方法, 核心思想是将处理器视为以1 比特为单位的单指令多数据处理器, 随后被Matthew Kwan 称为比特切片(bit slicing)[4].比特切片方法在64 位平台上实现了64 组DES 消息的并行加解密, 将逻辑门个数从理论上需要的132 个每比特输出优化到100 个每比特输出.之后研究者们对门函数个数进一步进行了优化, 使得标准逻辑门(与、或、非、异或) 和非标准逻辑门均达到了平均50+ 个每比特输出.2011 年Roman Rusakov[5]又将门函数的个数降至平均44 个逻辑门每比特输出.比特切片方法可大大提高实现效率, 也可用于搜索密钥, 对RISC 和CISC 的指令集平台均适用, 且具有更好的安全性.
为了提高软件实现速度, 国内外许多学者尝试将采用SIMD (Single Instruction Multiple Dada, 单指令多数据) 技术用于密码算法的软件实现.A. Adomnicai 和T. Peyrin[6]给出改进的比特切片方法“Fixslicing”,在ARM 和RISC-V 平台实现了AES.2012 年Intel 推出高级向量指令集(Advanced Vector Extensions,AVX) 后, 众多学者开始研究如何利用AVX 指令集加速对称分组密码算法的实现速度, 尤其是轻量级密码算法的实现速度.Seiichi Matsuda 和Shiho Moriai[7]利用AVX 指令集加速切片实现, 给出了轻量级密码算法面向云端的实现, 将SSE 指令与比特切片方法结合并应用到PRESENT/Piccolo, 使两者的实现吞吐量分别达到4.3 cycle/byte 和4.57 cycle/byte.2013 年,Neves 和Aumasson[8]将AVX2指令应用到SHA-3 候选算法BLAKE 上并提高了其实现性能.最近,郎欢等[9]利用X86 架构下的SIMD指令给出了高效的SM4 实现, 他们采用C 语言调用AVX2 指令接口方式实现, 在并行查表的基础上, 给出了两种不同的方法.2014 年Kostas Papapagiannopoulos 等人[10]将比特切片方法修改为nibble 切片方法, 并减少了访问内存, 在AVR 处理器上给出了高效实现.
此外, 研究者们将比特切片方法和其它方法结合, 对SM4 算法进行软件实现, 也取得了较好的效果.SM4 算法公布不久, Fen Liu 等[11]破解了SM4 算法S 盒的结构, 公布了S 盒的代数表达式及具体参数值.之后, Hao Liang 等[12]基于已破解的SM4 中S 盒结构, 提出了基于复合域的SM4 实现方法, 将S盒的有限域求逆运算变换到复合域中实现, 并在FPGA 上进行验证.Jingbin Zhang 等[13]提出了SM4在复合域中的软件实现, 使用X86 架构普通指令实现, 速率达到20 Mbps.最近, A. Eldosouky 和W.Saad[14]针对物联网应用的效率、安全需求改进了轻量级密码算法LED 的比特切片方法, 并在嵌入式处理器ARM Cortex-A53 进行了实现验证.O. Hajihassani 等[15]利用比特切片方法进一步提高了高级加密算法AES 的加解密吞吐率.总的来说, 在国密标准SM4 算法的软件优化实现方法取得了一些进展, 但和其他对称加密算法如AES 相比, SM4 的软件优化实现仍需进一步研究.
本文利用比特切片方法, 结合支持单指令多数据(SIMD) 的AVX2 指令集, 提出了一种SM4 算法的快速软件优化实现方法, 使用256 位的YMM 寄存器实现了SM4 算法的256 分组数据并行加解密.该方法首先对待加密的明文消息通过SIMD 版本的数据编排算法进行预处理; 之后提出了一种改进的化简逻辑表达式的新方法, 将实现逻辑表达式所需的逻辑门电路数量由3000 降至497; 最后使用反编排算法得到密文.在Intel Core i7-7700HQ(Kabylake)@2.80 GHz 处理器上, 结合x86 平台拓展指令集AVX2和上述方法对SM4 算法进行软件实现, 实现速度达到了2580 Mbps.相比于传统的查表实现(Intel Core i7-5500U(Broadwell-U)@2.40 GHz)、未优化的比特切片实现(Intel Core i7-5500U(Broadwell-U)@2.40 GHz)、SM4 软件优化实现公开文献的最佳结果[9](Intel Core i7-5500U (Broadwell-U) @2.40 GHz), 新方法的实现效率分别提升了1.8 倍、2.6 倍和43%.综上所述, 本文主要贡献如下:
(1) 提出了一种通用的对称分组密码算法的软件优化实现方法, 该方法通用于所有对称加密算法的快速软件实现.
(2) 提出的基于比特切片的软件优化实现方法无需内存或高速缓存查表, 因此可抵抗缓存-计时侧信道攻击[16], 从而安全性得到了提升.
(3) 提出的优化方法具有较强的通用性.该方法可用于所有对称加密算法的软件优化实现, 并适用于不同的软件架构: 在CISC 架构平台如X86 适合借助SSE、AVX2、AVX512 等拓展指令集实现, 在RISC 架构(ARM,RISC-V) 的平台可使用普通指令集实现.
(4) 新的选择函数和搜索算法具有通用性, 可用于一般逻辑函数的化简.
本文其余内容组织如下: 第2 节介绍SM4 算法及AVX2 指令; 第3 节介绍新的选择函数及基于选择函数的改进的搜索算法; 第4 节介绍SM4 的基于比特切片和AVX 指令的软件优化实现方法; 第5 节介绍实验结果; 第6 节总结全文.
2 预备知识
2.1 SM4 简介


对于每个S 盒的8 位输入, 前4 位作为行, 后4 位作为列, 输出即为查找表中对应行列所对应的值.S 盒如图2 所示.
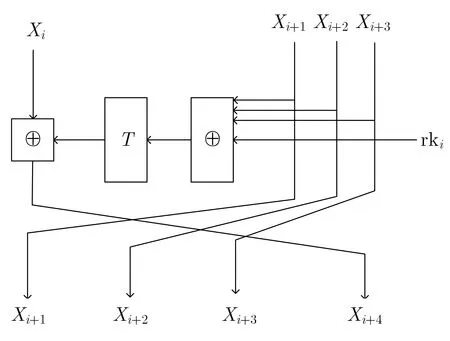
图1 SM4 轮函数Figure 1 Round function in SM4 algorithm

图2 SM4 代替表Figure 2 Substitution table in SM4 algorithm

2.2 SIMD 技术及AVX2 指令集
SIMD (single instruction multiple data) 技术可实现同一操作并行处理多组数据.目前支持SIMD技术的处理器厂商主要有Intel、AMD、ARM 等.目前大多数PC 及服务器采用的是Intel 处理器, 而Intel 处理器中的SSE/AVX 指令集采用的正是SIMD 技术.AVX (Advanced Vector Extensions) 指令集[18]是256-bit 宽向量指令集, 指令操作对象称为YMM 的256-bit SIMD 寄存器.该寄存器内容分为2 个128-bit lane.AVX 指令操作对象为lanes, 该指令不支持跨越lanes 的操作.
AVX2 指令集是AVX 指令集的扩展和改进, 也称为Haswell New Instructions, 支持跨越lanes 的操作.AVX2 支持8 道32-bit 整数异或(vpxor)、移位(vpslld)、置换(vpermd)、查表(vpgatherdd) 等.2013 年Inter 在22 nm Haswell 微架构处理器上正式推出AVX2 指令集.表1 给出了部分AVX2 指令,这些指令可用于对称分组密码的切片实现.
3 构造新的选择函数及搜索算法
“选择函数”[19]是Mattew 为比特切片方法中简化实现S 盒逻辑门电路数量而提出的一种逻辑函数表达形式.选择函数的思想为二分法, 每次分得两个子函数, 直至最终分解到的子函数可以直接实现.经研究发现, 对于上述特定问题选择函数形式比其他常用的标准形式优越许多.如上所述, 对于SM4 算法的S 盒, 使用最简与或形式、最简或与形式、最简与或非形式等需要逻辑门数约为3000, 而使用已知的3个选择函数形式时, 可将逻辑门数限制在:NSM4= 12+8×(21+22+···+28−2) = 1032.使用本文提出的新的选择函数及改进的搜索算法, 可进一步将逻辑门数减至497 门.一般来说, 使用的选择函数越多,搜索越充分, 越能减少逻辑门数量.

表1 相关AVX2 指令总结Table 1 Summary of relevant AVX2 instructions
本节首先基于已有的选择函数构造新的选择函数, 之后基于新的选择函数给出改进的搜索算法, 最后介绍如何使用新的选择函数及改进的搜索算法化简S 盒的逻辑表达式.
3.1 选择函数简介
为化简比特切片方法中实现S 盒所用的逻辑门电路数量, Mattew 提出了化简逻辑门电路的算法及“选择函数” 的概念.使用选择函数, DES 中实现S 盒的逻辑门电路数量从平均70 门每比特输出被约简到平均45 门每比特输出.
设Fo为8 比特逻辑函数, 即Fo(abcdefgh), 从输入abcdefgh中任选一个比特, 记为sel, 给出选择函数基本形式:

Mattew 指出, 还可使用nand、nor 等非标准逻辑门构造更多选择函数.生成选择函数形式的逻辑表达式过程如下: 从需要实现的逻辑函数出发, 进行选择, 逆向生成整个逻辑电路, 直至最终得到许多2 比特逻辑函数.理论上共有16 种不同的2 比特逻辑函数, 其中有4 个是平凡的(常量0、1 和直接连接两个输入), 另外12 个非平凡的逻辑函数可由两个输入连接12 个逻辑门实现, 如图3 所示.每次选择时都有上述3 个选择函数形式可以使用, 需要逐个尝试以取得较好结果.对于DES 的6 比特输入4 比特输出S盒来说, 先后处理4 个输出, 每个输出最多需要4 次“选择”.处理过程中, 对1 个逻辑函数做“选择” 前,可以尝试直接连接到之前已实现的中间结果, 这是化简的主要实现方式.

图3 16 种2 输入逻辑门的一种实现Figure 3 Example of 16 logic combinations of two gates
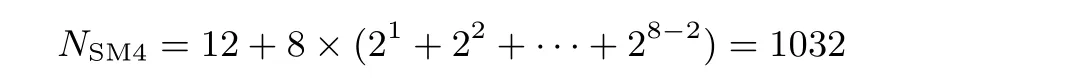
通过对选择函数的分析, 我们发现换入不同逻辑门, 得到的新选择函数与原形式可能有不同的子函数, 从而带来不同的结果.
针对上述问题, 本文对选择函数及其搜索算法进行了研究, 给出了9 种实质不同的“选择函数” 表达式, 并改进了基于“选择函数” 的逻辑门电路生成算法(称为搜索算法), 以利用9 种“逻辑表达式” 得到更简化的S 盒逻辑表达式.
3.2 构造新的选择函数及搜索算法
本小节介绍对“选择函数” 的扩展和搜索算法的改进.
3.2.1 构造新的选择函数
令m表示逻辑函数输入的比特数.由于“选择函数” 表达式每次将函数Fo分解为F1、F2、F3, 每次减少1 比特输入, 从而保证在有限次(m −2 次) 选择后得到可直接实现的表达式.对于输入为m比特的Fo, 可用2m比特表示; 限定F1、F2、F3的输入为m −1 比特时, 它们均可用2m−1比特表示, 且F1,F2,F3唯一.
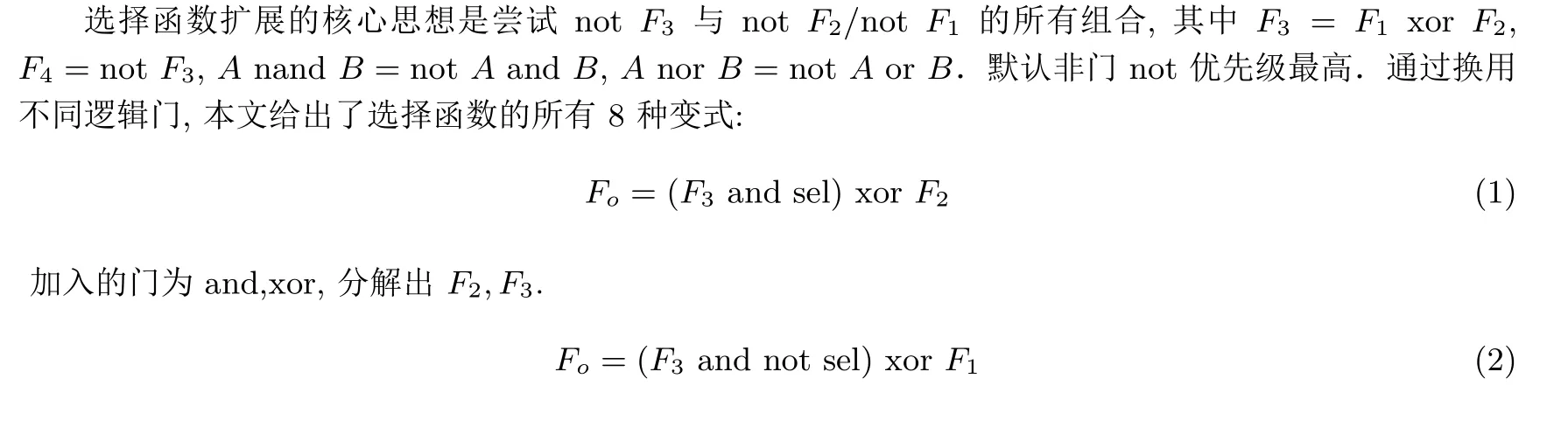

换入非标准逻辑门, 可以找到的所有表达形式都包含于上述9 种形式之中.
这种递归生成“选择函数” 的算法处理Fo与notFo可能得到差异较大的结果, 即Fo与notFo对于“选择函数” 生成表达式的算法来说是两个不同的表达式, 因此应分别尝试.
3.2.2 改进搜索算法
下面给出改进的搜索算法(算法1). 对40 320×40 320 种输入输出排序, 分别调用此生成算法, 搜索其中逻辑门数最少的逻辑电路.算法输入逻辑电路、sel 比特排序和输出排序, 输出逻辑电路和逻辑电路的总门数.算法包括5 个步骤.

注: 改进之处在于4 中提供更多选择函数形式, 5 是新加入的步骤.
4 SM4 算法的优化实现
本节首先介绍SM4 算法优化实现方法的总体结构, 之后介绍具体的优化实现.
4.1 总体实现
SM4 算法的优化实现包括三部分: 数据编排、迭代计算、数据反编排.对于数据(反) 编排部分, 主要采用SIMD 技术实现转置并优化; 对于迭代部分, 主要使用选择函数优化法优化S 盒的逻辑表达式.具体过程如图4 所示.

图4 总体实现结构Figure 4 Overall structure of implementation
4.1.1 数据编排

4.1.5 数据反编排
从切片后的 128 组 256 比特数据恢复到 256×128 比特数据, 需要构造比特矩阵转置变换inv_TRANS(), 输入为128×256 比特, 输出为256×128 比特.若将输入第i比特表示为二维数组M[128][256]的M[i/256][imod256]项, 则转置为二位数组M[256][128]的M[imod256][i/256]项.
4.2 AVX2 指令集的的使用
4.2.1 实现数据(反) 编排
数据编排中, 对256×128 比特数据, 分为两个比特方阵, 对方阵进行比特粒度的转置[20].使用vpor、vpslld、vpxor 等AVX2 指令优化实现转置算法.
数据反编排中的128×256 比特数据也可分成两个比特方阵类似处理.
4.2.2 实现密钥编排
若并行加解密的分组使用不同密钥, 编排方法同数据编排, 不需要反编排; 若并行加解密的分组使用相同密钥, 编排不需要比特粒度转置, 可以将密钥每一比特复制为256 比特, AVX2 指令或普通指令均可平凡地实现.
4.2.3 实现S 盒
使用AVX2 指令集中提供的逻辑指令实现, 具体为vpor, vpand, vpxor, vpnand.指令为三操作数指令(其中一个为目的操作数), 不修改源操作数, 必须选择16 个YMM 寄存器作为操作数.需要在内存中暂存数据, 可使用指令vmovdqa、vmovdqu 进行数据加载、存储.
4.3 化简S 盒逻辑表达式
下面介绍如何使用新的“选择函数” 及改进的搜索算法化简S 盒逻辑表达式.利用上节给出的9 种选择函数表达式, 可得到9 种改进的表达式.下面以式(1) 为例:
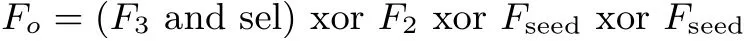

在上述四种处理方式中, 前两种利用已存在的逻辑门, 无需额外代价; 后两者基于选择函数的递归处理在没有直接可用的逻辑门的情况下使用.
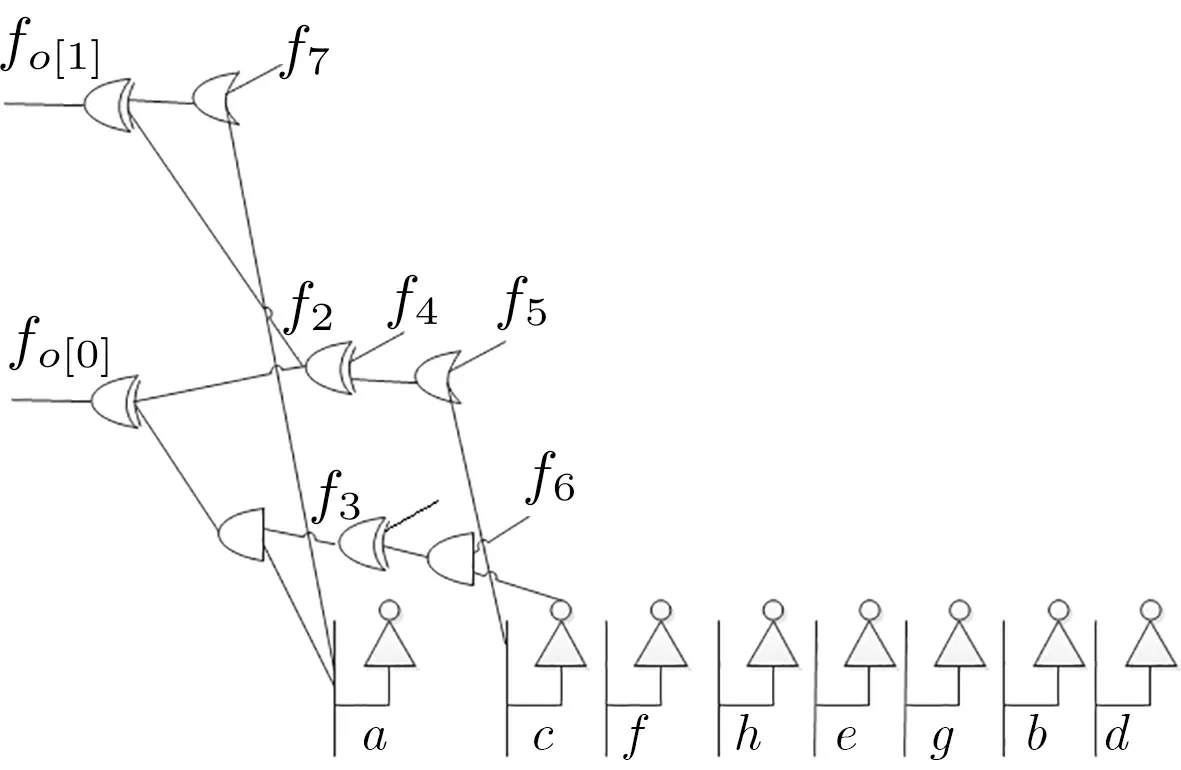
图5 连接到已存在的逻辑门Figure 5 Appending to generated logic gates
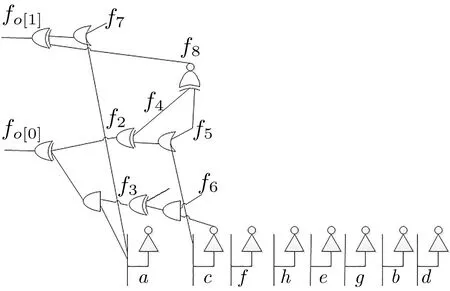
图6 连接到两个逻辑门的组合Figure 6 Appending to combination of two logical gates
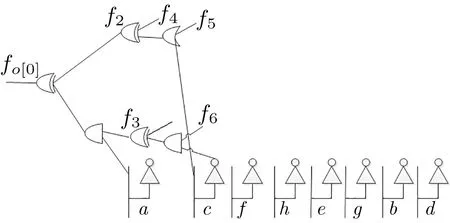
图7 使用选择函数公式递归生成逻辑电路Figure 7 Generating logical circuit using selection function recursively
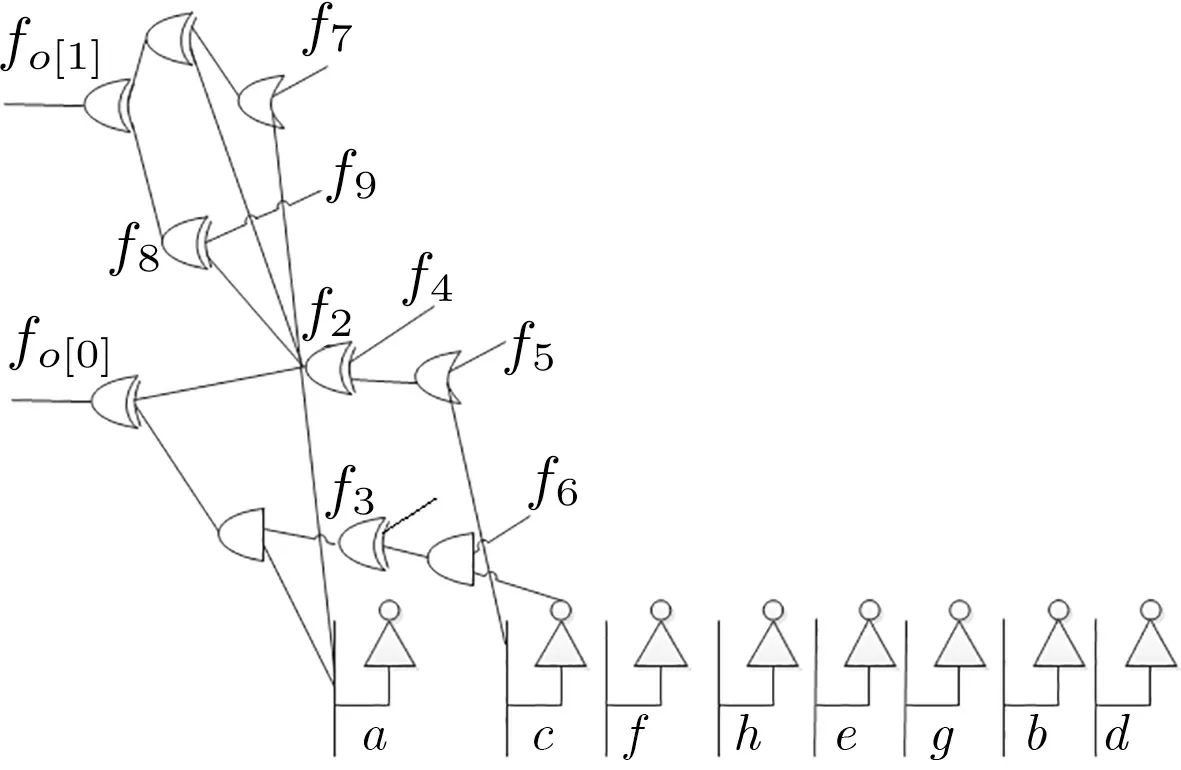
图8 引入可变的Fseed 生成逻辑电路Figure 8 Generating logical circuit via almost arbitrary Fseed
4.4 S 盒实现结果比较
表2 列出了使用选择函数和未使用选择函数时S 盒实现中需要的逻辑门电路数量及实现时间.由于AVX2 指令集中数据加载存储指令相对于逻辑操作指令迅速许多, 因此S 盒的实现时间大致由逻辑门数决定.未使用选择函数实现S 盒所需逻辑门数约为3000 (最简与或式), 使用9 个选择函数和改进的搜索算法所需的逻辑门数为497.对31 250 Mb 数据加密测试结果显示, 未使用选择函数的实现时间为30 秒,使用9 个选择函数和改进的搜索算法后, 实现时间减少至10.3 秒.

表2 S 盒实现所需要的逻辑门数及实现时间比较Table 2 Logical gate count and time for implementing S box
5 实验结果
本节比较已有公开文献中关于SM4 软件实现的效率, 包括传统查表法、SIMD 技术查表法及比特切片方法.利用C 语言和汇编语言对SM4 算法进行优化实现, 在相同的硬件环境中, 比较SM4 算法不同实现方法的效率.由于PC 端内存资源相对丰富, 故对于4 GB、8 GB 内存不做区分; 处理器微架构和主频对性能有较大影响.具体测试环境如表3 所示.
表4 总结在不同处理器上SM4 算法采用查表法、选择函数优化法的软件实现性能.评估分组密码算法软件实现性能的指标是每秒钟加/解密的比特数, 即bps.对31 250 Mbit 数据进行加密测试.表4 的8-32 表示采用8-bit 输入32-bit 输出表.
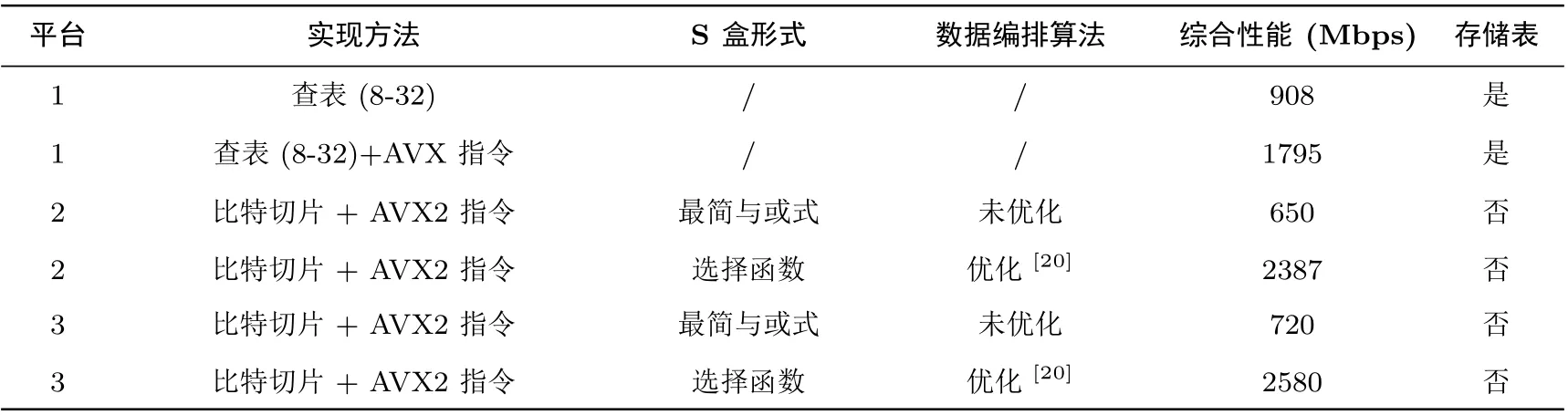
表4 软件实现方法在不同处理器上效率对比Table 4 Efficiency of software implementations on different processors
由表4 可以看出, 使用AVX2 指令的并行查表方法比普通查表方法在效率上有明显提升, 由908 Mbps 到1795 Mbps 提升接近1 倍.未优化的比特切片+AVX2 指令方法效率不佳, 而本文的比特切片+AVX 指令+ 选择函数优化方法在Intel Core i5-6200U(Skylake)@2.40 GHz 和Intel Core i7-7700HQ(Kabylake)@2.80 GHz 分别达到2387 Mbps 和2580 Mbps, 相对于近似的主频(2.40 GHz)、微架构(Intel Core i7-5500U(Broadwell-U)) 的AVX2 指令并行查表方法有明显优势.
对于算法所需的内存开销, 普通查表和并行查表需要4 KB 内存存放代换表, 对于资源受限的终端并不合适; 而本文的比特切片实现无需任何额外的内存开销来存储代换表, 因此所需内存开销为0.此外,查表法在内存中存储代换表并需要在加解密时访问对应的内存, 除了需要额外的内存开销, 还不能抵抗缓存-计时侧信道攻击.本文的软件优化实现方法不需查表, 因此能够抵抗该类侧信道攻击.
下面进一步给出对31 250 Mb 数据加密测试的详细结果.

表5 软件实现方法效率测试Table 5 Test on efficiency of software implementations
由表5 可知, 在Intel Core i5-6200U(Skylake)@2.40 GHz 下, 本文的基于选择函数优化法的实现时间为13.09 秒, 加密效率提升2.04 倍.在Intel Core i7-7700HQ(Kabylake)@2.80 GHz 下, 该方法的实现时间为12.11 秒, 加密效率提升2.18 倍.此外, 由表5 可以看出, S 盒计算占全部计算约80%, 进一步提升效率的关键仍在于优化S 盒的实现.
6 总结
本文基于比特切片方法和SIMD 技术, 提出了一种新的SM4 算法软件优化实现方法, 并利用X86 平台的AVX2 指令集给出了高效的实现.新方法首先利用AVX2 指令优化了数据编排算法, 之后基于选择函数提出了更灵活的化简S 盒逻辑表达式的算法.在基于选择函数的优化方法中, 构造了新的选择函数,并基于新的选择函数改进了搜索算法, 从而将S 盒所使用的门电路数量从3000 门降至497 门; 在Intel Core i7-7700HQ(Kabylake)@2.80 GHz 环境下, 同目前公开文献中SM4 软件实现的最快速度1.7 G 相比, 基于选择函数的优化方法加解密速度提升至2.5 G, 提高了43%.同基于查表的软件实现方法相比, 本作品的软件实现方法可以抵抗cache 攻击, 从而提高了算法实现的安全性.本文提出的新的选择函数和搜索算法具有通用性, 可用于其它一般逻辑函数的化简.此外, 优化方法具有可扩展性, 不仅可以从SM4 算法扩展至目前所有的对称加密算法的软件优化实现, 而且可以从X86 平台的拓展指令集AVX2 实现扩展至利用RISC 指令集在资源受限、安全性要求高的ARM 等嵌入式平台上实现.
