基于概率可靠度的槽式太阳能电站优化设计

张燕平，张宇超，刘易飞

基于概率可靠度的槽式太阳能电站优化设计

张燕平1，张宇超2，刘易飞2

（1．华中科技大学能源与动力工程学院，湖北省 武汉市 430074；2．华中科技大学中欧清洁与可再生能源学院，湖北省 武汉市 430074）

基于概率可靠度对槽式太阳能电站系统配置进行了优化设计。首先，通过SAM软件对建设50MW槽式太阳能电站进行了模拟，并考虑不确定性因素带来的随机性，结合神经网络-蒙特卡罗法，建立了槽式太阳能电站基于其太阳倍数、蓄热系统蓄热时长以及集热槽行间距3个设计参数的不确定性模型。其次，建立了可靠度计算模型，选取平准化度电成本(levelized cost of energy，LCOE)、容量因子(capacity factor，CF)和总发电效率作为性能评价指标，以各性能评价指标的可靠性指标最优为优化目标，进行了可靠性计算与分析。最后，将不确定性模型下得出的各设计参数的最优配置与确定性模型下的优化结果进行了对比。由于考虑了不确定性因素的影响，不确定性模型下的计算结果更接近实际情况。

槽式太阳能电站；概率可靠度；优化设计；不确定性；神经网络

0 引言

近年来，太阳能开发利用规模快速扩大，技术进步和产业升级加快，太阳能热发电技术已取得较大进展[1-2]。槽式太阳能热发电技术是目前发展最成熟的太阳能热发电技术，已在许多国家实现了商业运行，并取得了很大收益。在槽式太阳能热发电系统中，集热场面积决定着整个系统输入能量的大小，但由于集热器成本较高，集热场的面积大小很大程度上决定着系统的总成本。蓄热装置可使系统在额定负荷下的运行时间更长，但增加蓄热装置会使系统更加复杂[3]。由于太阳能场的遮蔽效应和集热场的热能损失等问题，集热槽行间距的选择也会对系统的性能造成影响。因此，妥善解决这些参数的配置问题，选择较为合适的系统配置，对系统的运行性能和经济性的改善具有至关重要的意义。

目前，国内外许多学者对槽式太阳能电站的系统特性进行了研究。赵明智等[3]利用SAM软件对美国达科特地区建设50MW的槽式太阳能电站进行模拟，研究了选择系统最佳太阳倍数与蓄热时长的方法。李然等[4]综述了带熔融盐储热系统的槽式太阳能热发电技术系统流程，得出了使电价最低的集热场面积与蓄热时长的最佳配置。IZQUIERDO等[5]从年发电量和功率因子的关系出发，研究了槽式和塔式电站最佳的集热场面积。以上学者均采用确定性方法对槽式太阳能电站进行研究，然而确定性模型的研究方法并未考虑系统输入变量的不确定性[6]。而不确定性分析方法能满足这种客观要求。在使用不确定性分析方法进行优化时，由于考虑了随机性因素的影响，输入变量并不是一个确定性的数值，而是一个区间变化的值，该区间变化的值反映了输入变量值的可能范围。由此可对系统性能评价指标进行区间预测，从而可以更好地判断可能存在的不确定性因素对系统造成的影响，进而对优化结果做出更合理的决策。目前不确定性研究方法的发展较成熟，已在其他领域广泛使用。HANAK等[7]基于燃煤电厂输入的不确定性，研究了电厂设备故障的概率，该研究为有效降低电厂投资和运营成本提供了参考。牛文娟等[8]通过建立电厂不确定性优化模型得出，在需求响应电厂模型中考虑不确定性的影响，可提高系统可靠性、降低系统风险成本。FREY等[9]对燃煤电厂排放控制系统的性能和成本进行了随机分析，结果表明不确定性建模的随机方法能更深入地了解系统的过程性能。

鉴于传统确定性方法并未考虑不确定性因素对电站带来的干扰，而在槽式太阳能热发电领域还鲜有使用不确定性分析方法进行系统优化的先例，本文建立了槽式太阳能电站基于其太阳倍数、蓄热系统蓄热时长以及集热槽行间距3个参数的不确定性模型，并基于概率可靠度研究这3个参数在给定性能评价指标下的最优配置。

1 槽式太阳能热发电系统

1.1 系统组成及模拟软件介绍

本文将对图1所示的50MW槽式太阳能热发电系统进行计算分析，该槽式太阳能热发电系统由太阳能集热场、蓄热系统、发电系统等组成。蓄热系统使用的是双罐蓄热系统，其中冷罐用来存储来自集热场多余的热量，热罐用来在夜晚或者光照较弱时将热量传至发电系统发电。本文模拟软件使用的是美国国家可再生能源实验室(national renewable energy laboratory，NREL)开发的SAM软件，该软件可以通过输入环境参数、各子系统运行参数以及经济参数来对电厂的运行进行模拟，从而可以对系统的运行、经济性能进行计算与分析。

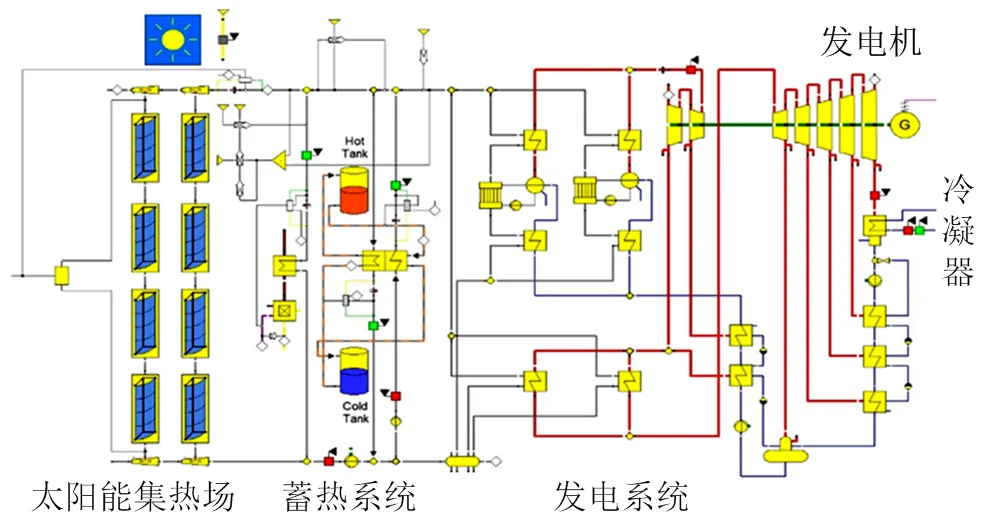
图1 槽式太阳能热发电系统

1.2 系统模拟参数说明

太阳能热发电厂的选址通常要考虑当地的太阳辐射强度。我国西北部以及内蒙地区太阳能资源丰富，适宜建造太阳能热发电站。在本文所研究的槽式太阳能电站中，选用了我国拉萨地区的气象数据，这些数据来源于NREL太阳辐射数据库(NSRDB)。相关设计参数见表1。

在槽式太阳能热电系统中，通常用太阳倍数来表征集热场面积，其计算公式如下：

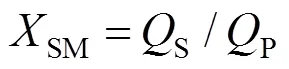
式中：SM为太阳倍数；S为集热场的集热功率，由集热场面积决定；P为汽轮发电机组额定进口热功率，由电站设计容量决定。由于集热器成本较高，考虑到占地和初始投资等实际情况，建设槽式电站时太阳倍数不宜过大。

为了解决集热场面积、蓄热系统容量及集热槽行间距3个参数的配置问题，选择较为合适的系统配置，本文分别选取太阳倍数、蓄热系统最大蓄热时长、集热槽行间距作为输入变量，研究其对槽式太阳能电站性能评价指标的影响，并基于各性能评价指标研究其最佳配置。

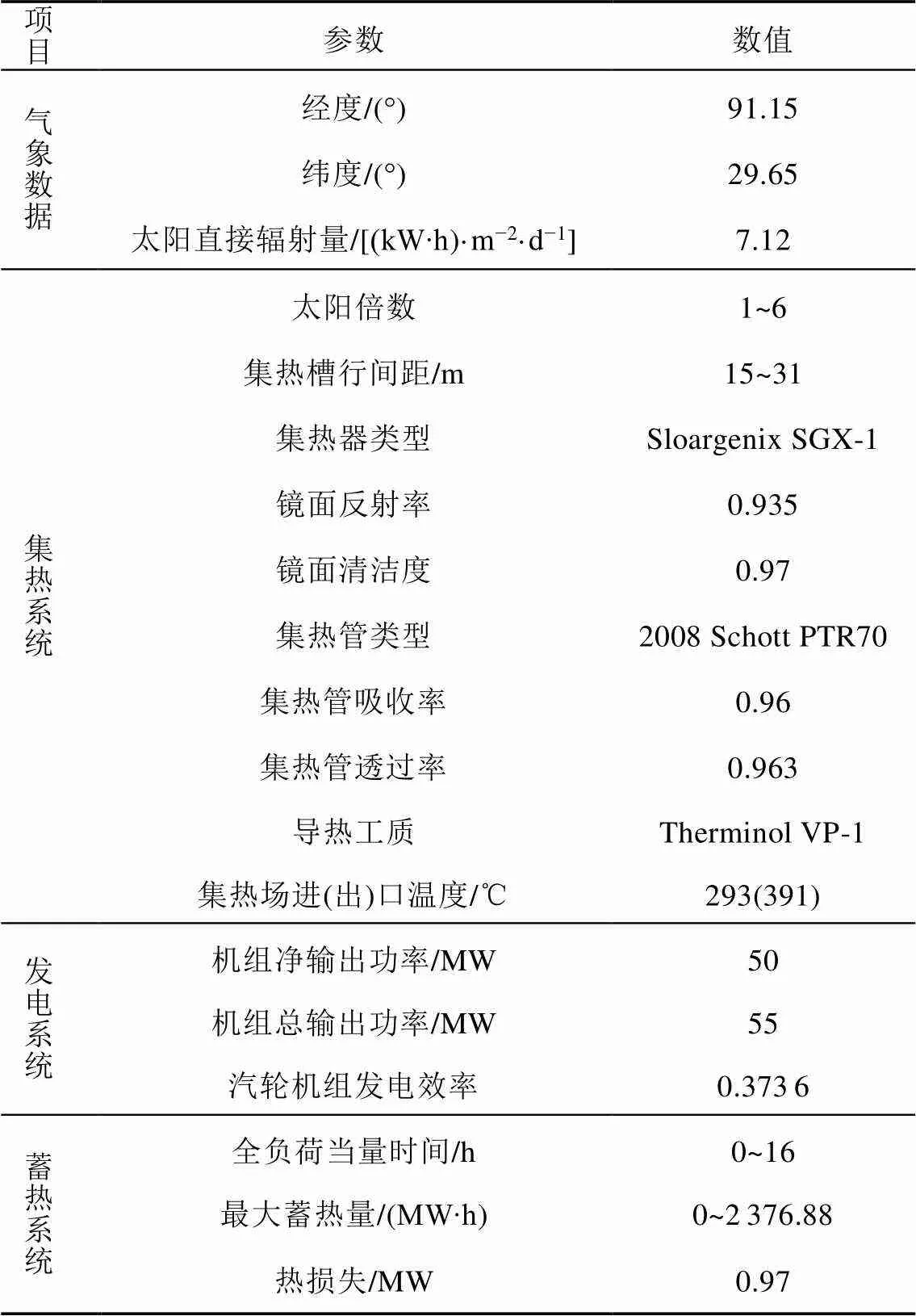
表1 槽式太阳能热发电系统设计参数

1.3 系统性能评价指标及其允许极限的确定

为表征太阳能电站的发电性能，选取容量因子(capacity factor，CF)、平准化度电成本(levelized cost of energy，LCOE)、总发电效率作为槽式太阳能电站的性能评价指标。容量因子表征了太阳能电厂的年发电能力，计算公式如下：

式中：CF为容量因子；t为年总发电量；r为电厂额定发电功率。

平准化度电成本为项目生命周期内的成本和发电量进行平准化后得到的发电成本，其计算公式如下：

式中：LCOE为平准化度电成本；i为总投资成本；O&M为运营和维修成本。

本文中，系统容量因子和平准化度电成本可以通过SAM模拟直接计算得出，而总发电效率计算公式如下：

式中：为太阳倍数为1时的集热面积；DNI为年太阳直接辐射总量。电站相关经济性参数取值参考文献[10-11]。

在槽式太阳能热发电领域，国内外许多专家学者均对电站的容量因子、平准化度电成本、总发电效率进行了研究。BOUKELIA等[12]在阿尔及利亚地区模拟建造槽式太阳能电站，在太阳倍数为1~3.6的范围内，得出其容量因子可达54.60%，LCOE可低至8.48美分/(kW∙h)。王慧富等[13]则在拉萨地区模拟建造槽式太阳能电站，得出太阳倍数在3~5的范围内，其最大总发电效率可达到13.5%。

为了对本文槽式太阳能电站进行可靠性分析与计算，分别对各性能评价指标选择其允许极限，结果见表2。

表2 各性能评价指标的允许极限

2 基于概率可靠度的不确定性优化模型

2.1 概率可靠性分析模型

电力系统中的可靠性分析是指用概率统计方法对发电系统按规定的供电质量标准连续供电能力的定量分析或评估。在进行可靠性分析时，通过相应的功能函数可以对每个参数逐一进行可靠性评估，设=(1,2,…,x)为电厂的输入向量，功能函数可以表示为

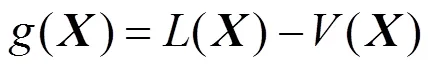
式中：()为输出变量的允许极限，通常由设计标准和实践决定；()为相应输出变量的实际预测值。在本文中，输入向量=(1,2,3)，其中1,2,3分别为电厂的太阳倍数、蓄热系统蓄热时长及集热槽行间距。输出向量则分别为容量因子、LCOE和总发电效率。()=0为极限状态面，它将基本变量空间分为失效区和安全区。若平准化度电成本实际预测值超过其允许上限值，即当()<0时，为失效。若容量因子和总发电效率实际预测值低于其允许下限值，即当()>0时，为失效。各性能评价指标的可靠度表示为

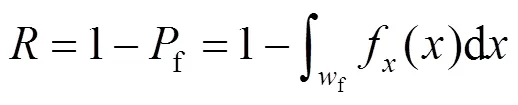
式中：f为失效概率；f为失效区；f()为3个基本变量的联合概率密度函数。

可靠性指标表示了平均可靠性裕度与极限状态表面的距离，其值越大，说明系统性能越好，各性能评价指标的可靠性指标计算公式如下：

2.2 不确定性分析模型

在传统的SAM软件建立的确定性模型中，设计参数往往是以定值代入模型进行计算的，而在实际应用中，由于受不确定性因素的干扰，各设计参数往往会在一定范围内动态波动，因此计算结果往往存在误差。为了表示各设计参数的不确定性，可以近似地将各设计参数的波动看作是给定均值和方差的正态分布变化。因此，可以利用蒙特卡罗随机抽样的方法，根据各设计参数的统计分布生成随机数组，用于表示一段时间内各设计参数值的变化[15]。本文中选取的随机数组为3000组。

为了建立槽式太阳能热发电系统输入、输出之间的函数映射关系，以对性能评价指标进行预测，本文建立了神经网络预测模型。选取太阳倍数、蓄热系统蓄热时长、集热槽行间距3个设计参数的值分别为1~6、0~16h、15~31m，并进行了排列组合，共设计1925组不同配置的样本，代入SAM软件中进行参数化模拟，分别计算出各性能评价指标的值，并将结果作为网络的训练数据，建立可以对系统各性能评价指标进行确定性预测的神经网络模型。采用BP神经网络中的Levenberg-Marquardt算法来训练网络模型，设置隐含层神经元为30个。图2为神经网络拓扑结构图。

图2 神经网络拓扑结构图

将各设计参数配置在给定分布下随机生成的3000组数代入已建立的神经网络模型，借助神经网络映射的函数关系，可以对各性能评价指标进行预测，从而建立了槽式太阳能热发电厂基于其3个设计参数的不确定性模型。最后，根据式(5)判断每一次预测是否失效。再依据

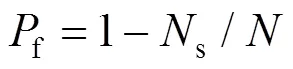
对各性能评价指标进行可靠度计算，式中：s为总失效次数；为总次数。

在考虑了极限状态的失效概率后，可用式(7)来评估各性能评价指标的可靠性指标。其中，选取的各设计参数的均值范围与方差[16-17]见表3。系统可靠性计算流程见图3。

表3 各设计参数的分布参数

2.3 优化模型

可靠性指标的值越大，失效概率越小[7]。为了对系统各性能评价指标进行优化，保证最低的失效概率，有必要找出使系统性能评价指标最优的设计参数配置。由于设计参数配置很难同时保证各性能评价指标的可靠度，因此基于不同性能评价指标，结合可靠度计算模型，分别找出使系统性能评价指标的可靠性指标最大的设计参数配置。其优化目标如下：

3 优化结果分析与对比

3.1 不同性能评价指标最优配置的可靠性分析

在表3设计参数所在均值范围与设定方差下，根据概率可靠度计算模型及优化模型，分别找出使各性能评价指标的可靠性指标最优的设计参数配置。其结果见表4。

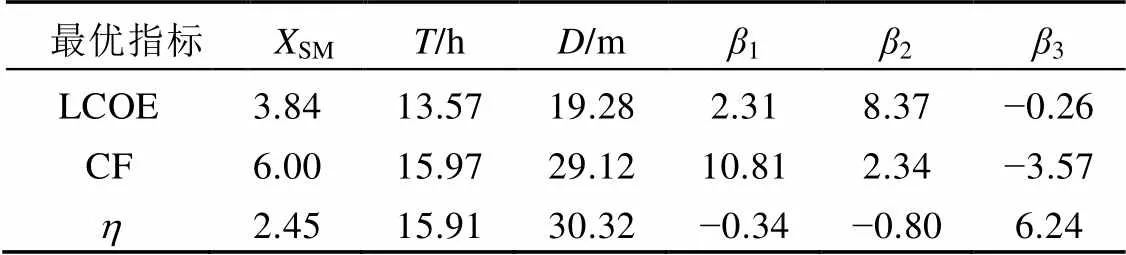
表4 基于不同性能评价指标的最优配置及其可靠性计算结果

图4—6为基于LCOE最优的设计参数配置下各性能评价指标的累积概率与发生概率分布，其中黑色虚线为允许极限。由图4可见，受不确定性因素的影响，平准化度电成本的值近似以正态分布在14~15.5美分/(kW∙h)的范围内变化，均远低于其允许极限，且平准化度电成本的值分布在14.3美分/(kW∙h)附近的概率高达0.9。因此，不确定性因素对该组配置下的平准化度电成本影响不显著。在本文设定允许极限下，该组配置的平准化度电成本的可靠度为0.988，可靠性指标为8.37，该组设计参数配置可实现最低的平准化度电成本。由图5可见，该组配置下容量因子会近似以正态分布在55%~75%的范围内变化，其中分布在67%附近的概率最大。该组配置下容量因子可靠度为0.973，可靠性指标为2.31。由图6可见，该组配置下电厂总发电效率近似以正态分布在10%~15.2%的范围内变化，其中分布在13.5%附近的概率最大。该组配置下总发电效率可靠度仅为0.44，可靠性指标为−0.26。

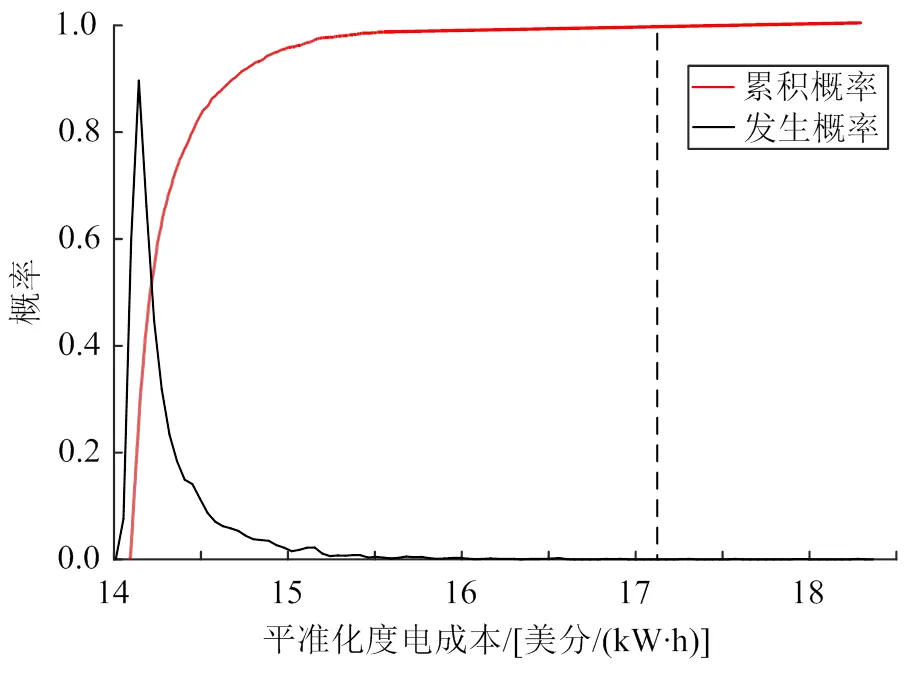
图4 基于LCOE最优的设计参数配置下LCOE的累积概率与发生概率分布

图5 基于LCOE最优的设计参数配置下容量因子的累积概率与发生概率分布

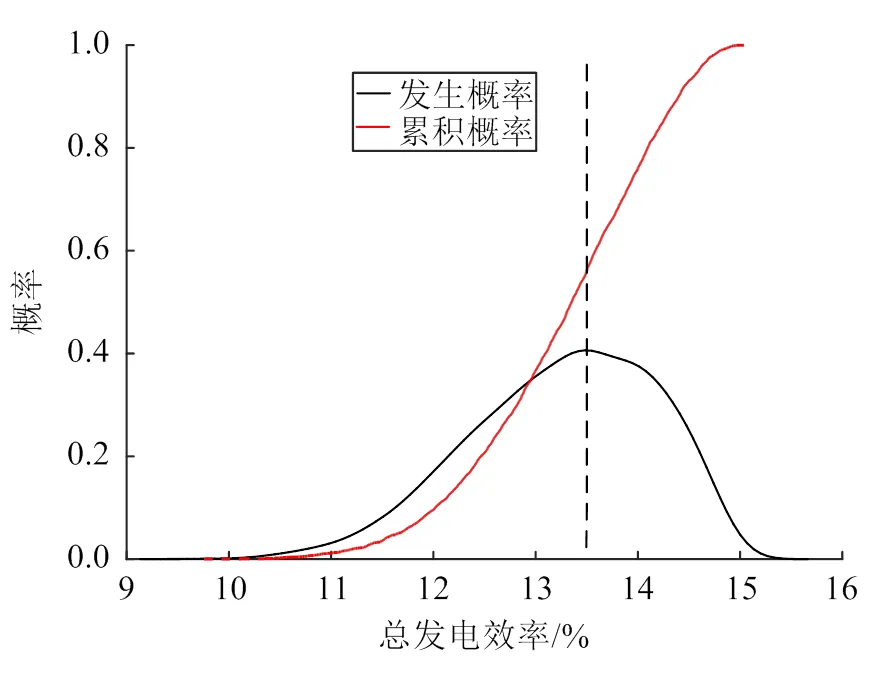
图6 基于LCOE最优的设计参数配置下总发电效率的累积概率与发生概率分布

图7—9为基于容量因子最优的设计参数配置下各性能评价指标的累积概率与发生概率分布，其中黑色虚线为允许极限。由图7可知，受不确定性因素的影响，该组配置下容量因子近似以正态分布在73%~86%的范围内变化，其中容量因子取值在79%处附近的概率最大，但不超过0.2。因此，不确定性因素对该组配置下的容量因子影响显著。在本文设定允许极限下，该组配置下容量因子的可靠度为1，可靠性指标为10.81，可实现系统最优的容量因子。由图8可知，该组配置下电厂的平准化度电成本近似以正态分布在14~18美分/(kW∙h)的范围内变化，其中分布在15.6美分/(kW∙h)附近的概率最大。该组配置下平准化度电成本的可靠度为0.98，可靠性指标为2.34。由图9可知，电厂的总发电效率近似以正态分布在8%~13%的范围内变化，其中分布在10.5%附近的概率最大。该组配置下总发电效率的可靠度为0，可靠性指标为−3.75。

图7 基于容量因子最优的设计参数配置下容量因子的累积概率与发生概率分布

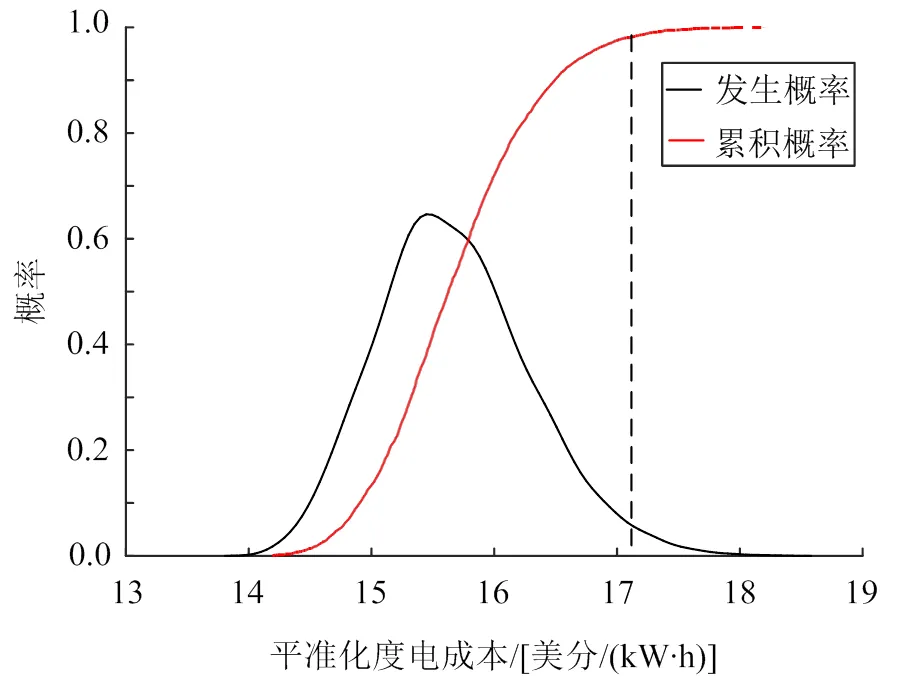
图8 基于容量因子最优的设计参数配置下LCOE的 累积概率与发生概率分布

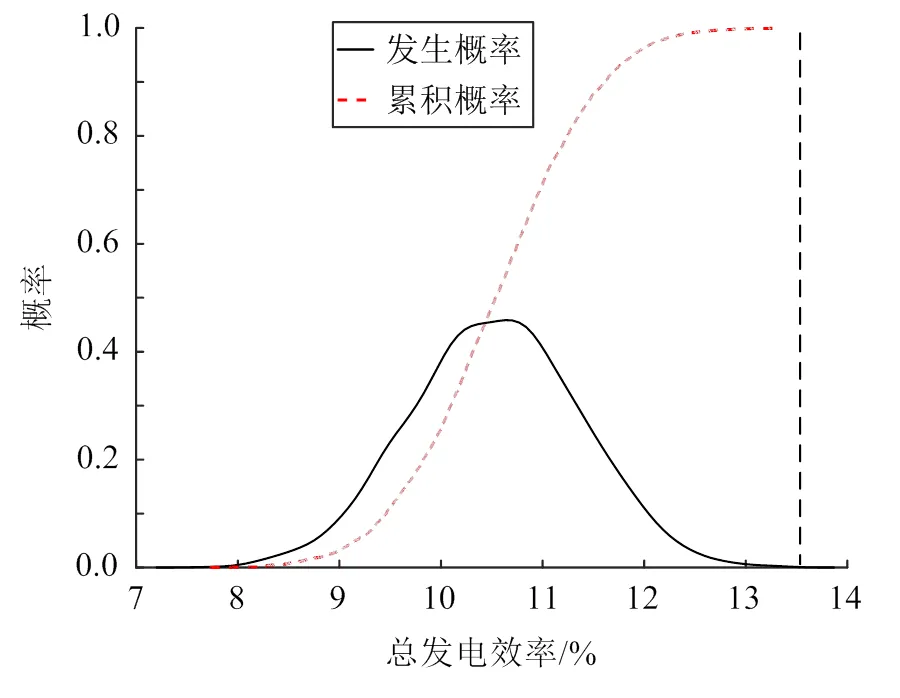
图9 基于容量因子最优的设计参数配置下总发电效率的累积概率与发生概率分布

图10—12为基于总发电效率最优的设计参数配置下各性能评价指标的累积概率与发生概率分布，其中黑色虚线为允许极限。由图10可知，受不确定性因素的影响，该组配置下电厂的总发电效率近似以正态分布在14%~15.5%的范围内变化。其中总发电效率分布在15.5%处的概率最大，约为0.7。因此，不确定性因素对该组配置下的总发电效率影响较小。在本文设定的允许极限下，总发电效率的可靠度为0.999，可靠性指标为6.24，该组配置能实现最优的总发电效率。由图11可知，该组配置下平准化度电成本近似以正态分布在13~27美分/(kW∙h)的范围内变化，其中分布在17美分/(kW∙h)附近的概率最大。该组配置下平准化度电成本的可靠度为0.43，可靠性指标为−0.80。由图12可知，该组配置下容量因子近似以正态分布在20%~70%范围变化，其中分布在50%的概率最大。该组配置下容量因子的可靠度仅为0.223，可靠性指标为−0.34。

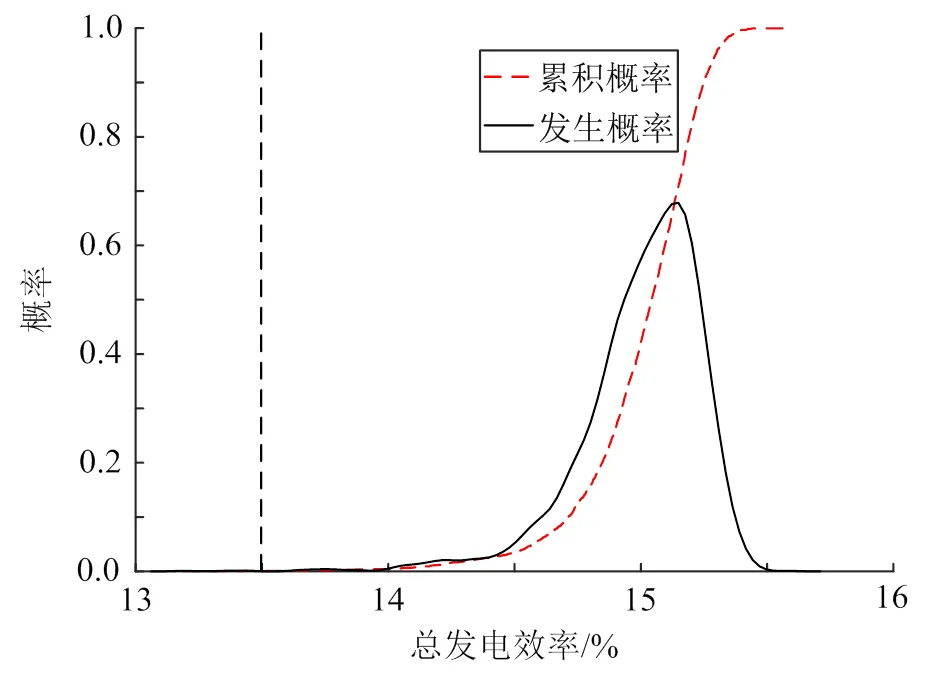
图10 基于总发电效率最优的设计参数配置下总发电效率的累积概率与发生概率分布

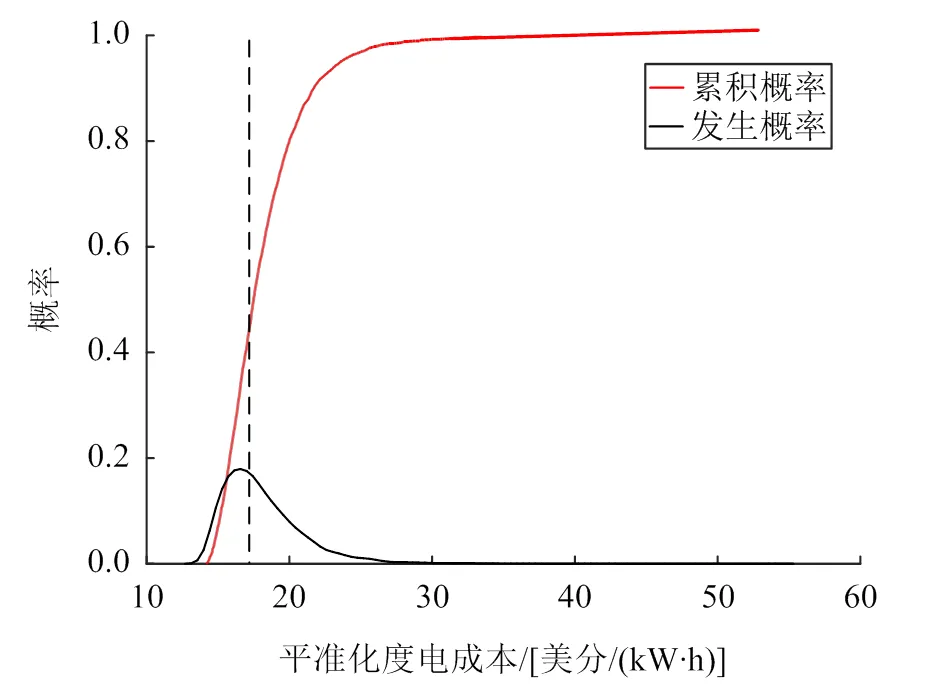
图11 基于总效率最优的设计参数配置下LCOE的累积概率与发生概率分布

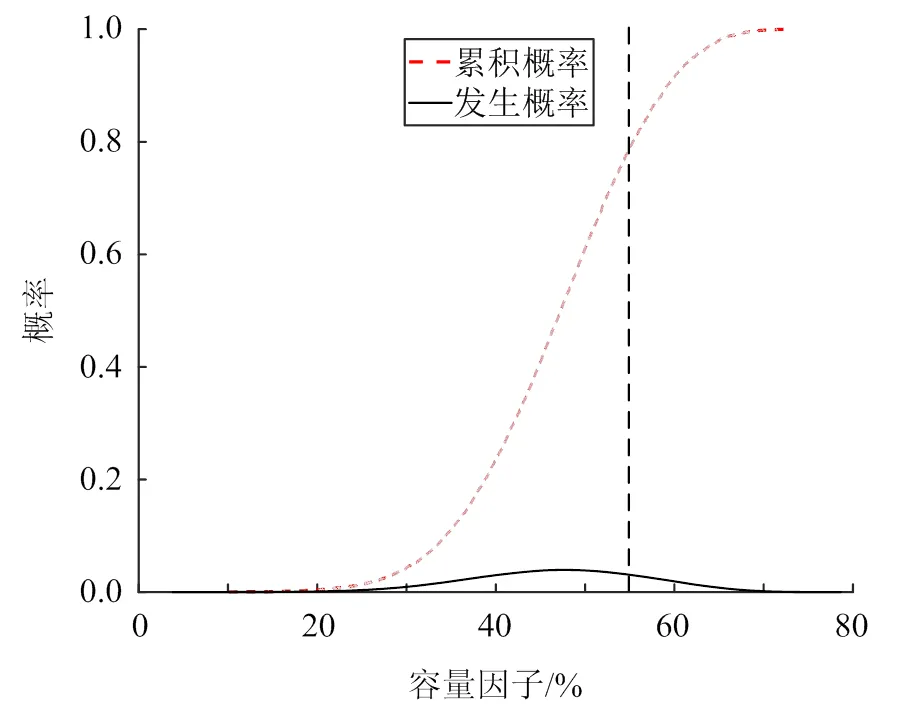
图12 基于总发电效率最优的设计参数配置下容量因子的累积概率与发生概率分布

3.2 确定性与不确定性模型的对比

对使用SAM确定性模型参数化模拟得到的结果进行优化，分别找出基于不同性能评价指标的最优设计参数配置，与本文基于概率可靠度建立的不确定性模型下的优化结果进行对比。其中在不确定性模型的优化结果中，将各设计参数配置下的3000组随机数计算的性能评价指标取其算术平均值，即为不确定性模型下性能评价指标的值。确定性与不确定性模型优化结果见表5。

由表5可知，在基于同一性能评价指标进行优化的设计参数配置下，与确定性模型相比，不确定性模型得出的太阳倍数与蓄热系统蓄热时长的值往往更小。

与确定性模型相比，不确定性模型各设计参数最优配置下性能评价指标的优化性能略低。由于确定性模型并未考虑随机因素的影响，因此优化结果会高估系统性能，计算结果与真实情况有较大的偏差。而不确定性模型考虑了输入参数的不确定性，其计算结果是近似呈正态分布的概率曲线，而非定值。概率分布曲线能更好地反映性能评价指标的分布特征，因此，与确定性模型相比，不确定性模型的计算结果往往与实际更接近。

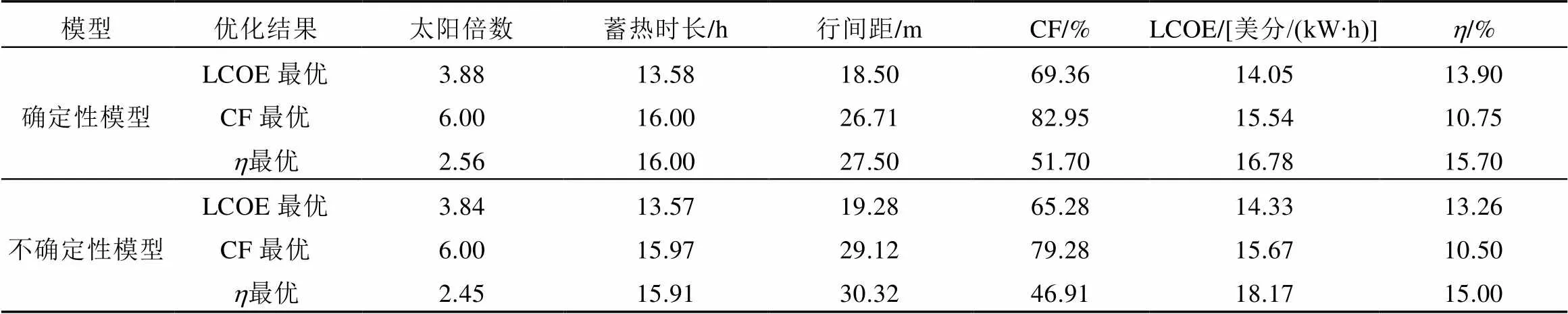
表5 确定性与不确定性模型优化结果对比

4 结论

在概率可靠度模型下，可以得出各性能评价指标的累积概率与发生概率图，从而可以看出其分布特征，因此在对电力系统进行参数设计时，可以综合考虑几个性能评价指标的可靠度与分布特征，从而对参数设计做出更全面的决策。

在所建立的不确定性模型下，基于系统各性能评价指标的最优可靠性指标，得出了系统在不同性能评价指标下最优的设计参数配置。即在各性能评价指标下，找到了太阳倍数、蓄热系统蓄热时长、集热槽行间距之间最佳的对应关系，这对优化LCOE和电站总发电效率及发电量至关重要。由于确定性模型并未考虑随机因素的影响，因此优化结果会高估系统的性能。而所建立的不确定性模型考虑了随机因素对系统输入参数的影响，其性能评价指标的计算结果近似呈正态分布，与确定性模型仅能得出一组确定的性能评价指标计算结果相比，不确定性模型的计算结果更符合实际。

[1]佟锴，杨立军，宋记锋，等．聚光太阳能集热场先进技术综述[J]．发电技术，2019，40(5)：413-425．

TONG K，YANG L J，SONG J F，et al．Review on advanced technology of concentrated solar power concentrators[J]．Power Generation Technology， 2019，40(5)：413-425．

[2]张哲旸，巨星，潘信宇，等．太阳能光伏–光热复合发电技术及其商业化应用[J]．发电技术，2020，41(3)： 220-230．

ZHANG Z Y，JU X，PAN X Y，et al．Photovoltaic/concentrated solar power hybrid technology and its commercial application[J]．Power Generation Technology，2020，41(3)：220-230．

[3]赵明智，张晓明，宋士金，等．槽式太阳能热发电系统太阳倍数和蓄热时长的选取方法研究[J]．太阳能技术产品与工程，2015(6)：50-54．

ZHAO M Z，ZHANG X M，SONG S J，et al．Study on the selection method of solar multiple and heat storage duration of trough solar thermal power generation system[J]．Solar Technology Products and Engineering，2015(6)：50-54．

[4]李然，封春菲，田增华．槽式太阳能热发电站系统配置的经济性分析[J]．电力勘测设计，2015(1)：71-75．

LI R，FENG C F，TIAN Z H．Economic analysis of system configuration of trough solar thermal power station[J]．Electric Power Survey and Design，2015(1)：71-75．

[5]IZQUIERDO S，MONTAÑŚ C，DOPAZO C，et al．Analysis of CSP plants for the definition of energy policies：the influence on electricity cost of solar multiples，capacity factors and energy storage[J]．Energy Policy，2010，38(10)：6215-6221．

[6]HU M，CHO H．A probability constrained multi-objective optimization model for CCHP system operation decision support[J]．Applied Energy，2014，116：230-242．

[7]HANAK D P，KOLIOS A J，BILIYOK C，et al．Probabilistic performance assessment of a coal-fired power plant[J]．Applied Energy，2015，139：350-364．

[8]牛文娟，李扬，王蓓蓓．考虑不确定性的需求响应虚拟电厂建模[J]．中国电机工程学报，2014，34(22)：3630-3637．

NIU W J，LI Y，WANG B B．Modeling of demand response virtual power plant considering uncertainty[J]．Proceedings of the CSEE，2014，34(22)：3630-3637．

[9]FREY H C，RUBIN E S．Probabilistic evaluation of advanced SO2/NOcontrol technology[J]．Journal of the Air & Waste Management Association，1991，41(12)：1585-1593．

[10]KURUP P，TURCHI C．Parabolic trough collector cost update for the system advisor model (SAM)[R]．Golden，Colorado，USA：National Renewable Energy Laboratory，2015．

[11]TURCHI C，HEATH G．Molten salt power tower cost model for the system advisor model[R]．Golden, Colorado，USA：National Renewable Energy Laboratory，2013．

[12]BOUKELIA T E，MECIBAH M S，KUMAR B N，et al．Optimization，selection and feasibility study of solar parabolic trough power plants for Algerian conditions[J]．Energy Conversion and Management，2015，101：450-459．

[13]王慧富，吴玉庭，张晓明．槽式太阳能热发电站的模拟优化[J]．太阳能学报，2018，39(7)：1788-1796．

WANG H F，WU Y T，ZHANG X M．Simulation and optimization of trough solar thermal power station[J]．Acta Energiae Solaris Sinica，2018，39(7)：1788-1796．

[14]国家发展改革委．关于太阳能热发电标杆上网电价政策的通知[Z]．北京：国家发展改革委，2016．

National Development and Reform Commission．Notice on the benchmarking on-grid tariff policy for solar thermal power generation[Z]．Beijing：National Development and Reform Commission，2016．

[15]段楠，薛会民，潘越．用蒙特卡洛法计算可靠度时模拟次数的选择[J]．煤矿机械，2002(3)：13-14．

DUAN N，XUE H M，PAN Y．The choice of simulation times when calculating reliability by Monte Carlo method[J]．Coal Mine Machinery，2002(3)：13-14．

[16]HELTON J，DAVIS F．Sampling-based methods for uncertainty and sensitivity analysis[R]．USA：Sandia National Laboratories，2000．

[17]WYSS G，JORGENSEN K．A user’s guide to LHS：Sandia’s Latin hypercube sampling software[R]．USA：Sandia National Laboratories，1998．

Optimization Design of Trough Solar Power Plant Based on Probabilistic Reliability

ZHANG Yanping1,ZHANG Yuchao2, LIU Yifei2

(1. School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan 430074,Hubei Province, China; 2. China-EU Institute of Clean and Renewable Energy, Huazhong University of Science and Technology, Wuhan 430074, Hubei Province, China)

Based on the probabilistic reliability, the configuration of the trough solar power plant was optimized. Firstly, the SAM software was used to simulate the 50 MW trough solar power plant. Then, by considering the randomness caused by the uncertainty factor, the uncertainty model of the trough solar power plant based on its solar multiple, the full load hours of storage system and the row spacing distance of the collector was established by neural network-Monte Carlo method. Secondly, the reliability calculation model was established, levelized cost of energy (LCOE), capacity factor (CF) and total generation efficiency were selected as key performance indicators (KPI), then the KPI were optimized based on the reliability indexes of each KPI. Finally, the optimal configuration of each design parameter obtained under the uncertainty model was compared with the optimization result under the deterministic model. Since the influence of the uncertainty factor is considered, the calculation result under the uncertainty model is closer to the actual situation.

trough solar power plant; probabilistic reliability; optimization design; uncertainty; neural network

10.12096/j.2096-4528.pgt.19143

TK 519

湖北省技术创新专项重大项目(2019AAA017)。

Project Supported by Major Projects of Technological Innovation in Hubei Province (2019AAA017).

2020-03-07。

(责任编辑 尚彩娟)