路面纹理扫描及宏观微观纹理分离

吴 凡 王国忠 李 强 于占强 许 珊

(1.大连理工大学交通运输学院，辽宁 大连 116024；2.山西省交通建设工程质量检测中心(有限公司)，山西 太原 030032； 3.中交二公局东萌工程有限公司，陕西 西安 710000；4.中交资产管理有限公司，北京 101300； 5.大连理工大学交通运输学院，辽宁 大连 116024)

随着交通量的增加，在雨雪天气时路面摩擦系数降低，抗滑能力下降，交通事故发生的概率也随之增加。对于抗滑性的评估是预测道路安全度高低的主要途径[1-3]，而路面纹理是评估路面抗滑性的重要指标。

美国材料与试验协会(ASTM)和国际标准化组织(ISO)指出路面抗滑性主要取决于路面纹理中的宏观纹理和微观纹理[4,5]。在高速行车条件下宏观纹理主要影响路面抗滑和排水，而在低速行车条件下微观纹理对于抗滑性能影响显著[6,7]。国内学者李波等[8]使用分形几何插值的方法对微观纹理和宏观纹理的四种组合路表纹理构造进行了精确的模拟,得到了路表纹理分形维数越大越能精确的预测路面抗滑性的结论。基于分形理论，黄宝涛等[9]探究了混合料表面材料的微观构造对沥青混合料抗滑性能的贡献。

上述研究成果均采用了数学模型分别讨论了宏观纹理与微观纹理对路面抗滑性的影响。

在图形纹理研究中，段春梅等[10]利用傅里叶变换检测随机纹理瓷砖的高精度表面缺陷。李鹏等[11]通过累计傅里叶变换计算每个信号的频谱相关函数，基于循环频谱特征提取路面的裂缝分类。胡宁等[12]通过对图像进行傅里叶变换，提出一套基于二维DFT指纹分割算法。徐贵力等[13]提出了利用傅里叶变换提取图形纹理特征新方法。研究表明基于傅里叶变换方法提出的数学模型能够有效提取图形纹理特征，能够基于频谱区间分割路面宏观纹理与微观纹理，为路面纹理研究提供了最新方法。

随着技术的进步，出现了具有高采样率和分辨率的扫描设备，可以同时捕获路表面的微观纹理和宏观纹理。本文首先利用3D激光扫描技术扫描路面采集路面纹理数据，并采用快速傅里叶变换的方法提取出路面的宏观纹理和微观纹理，这对道路抗滑机理研究及抗滑性能评估提供了基础。

1 路面纹理数据采集

1.1 芯样的收集

在山西现役高速公路上利用钻芯机钻取7个直径为10 cm的圆形芯样。芯样如图1所示。

1.2 扫描试件

采用三维激光扫描臂FARO Design ScanArm对芯样进行扫描，获取芯样表面各个点的三维坐标。其原理为三维激光扫描技术，三维激光扫描技术使用激光测距原理，在路表纹理变化监测中, 通过激光测距仪发射出一个激光脉冲信号, 通过路面纹理反射后, 进入数据接收器当中,再将数据进行处理分析，即可得到不同点的三维坐标和纹理信息，根据这些信息数据能够获得精确度较高的三维模型[14,15]。FARO激光扫描臂如图2所示。该扫描仪的扫描速率可达500 k pts/sec。点与点的间距为0.01 mm，可以同时捕获试样表面的微观和宏观纹理。

扫描得到的初始数据格式是芯样表面的三维坐标点。X坐标为扫描仪测量臂上固定的测点，Y坐标为扫描方向，Z坐标为芯样上表面竖向高度。在扫描过程中，测量臂沿着Y方向匀速平移，扫描仪在X和Y方向以0.01 mm的间距获取各个点的Z坐标。通过扫描获取了试件上大约4 500万个点的数据。利用这些点的三维坐标可以重构芯样的表面，建立芯样的三维空间数字模型，如图3所示。

1.3 纹理数据处理

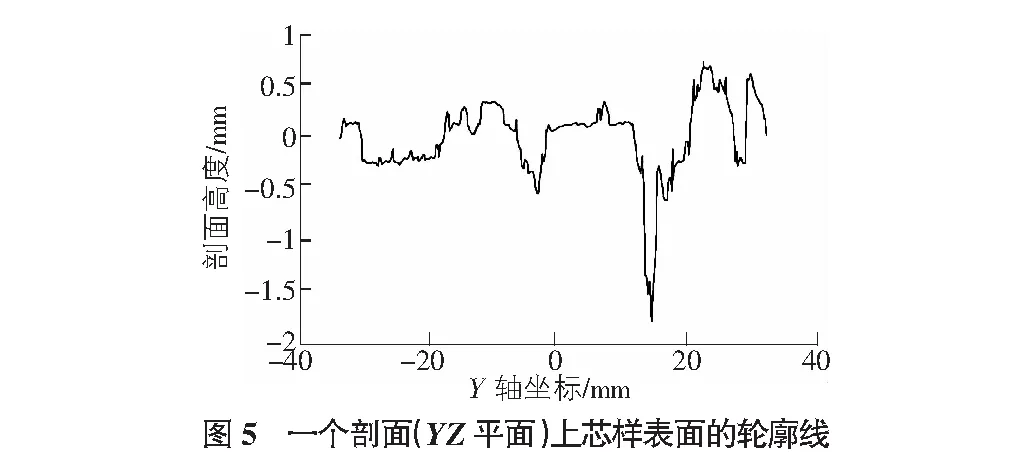
为便于直观的分析宏观纹理与微观纹理，选择试件的一个纵向剖面(YZ剖面)轮廓线进行研究。为避免圆形试件YZ剖面轮廓线长度不相等，需要对圆形芯样进行处理，找到圆形表面的内接正方形，如图4所示。在全部数据中，筛选出正方形内部的扫描点数据。并找到三维坐标点中X坐标相同的所有坐标点。这些数据点对应的YZ坐标可以构成YZ平面内的一条曲线，如图5所示，该曲线即为一个剖面处YZ剖面处芯样表面的轮廓线。

2 宏观纹理和微观纹理的分离

路面纹理按照波长可以划分为四种类型，包括微观纹理、宏观纹理、大构造和不平度[16]，波长在0.05 mm～0.5 mm之间为微观纹理，在0.5 mm～50 mm之间为宏观纹理，50 mm～500 mm之间为大构造，大于500 mm为不平整度。

为了讨论路面宏观纹理与微观纹理的影响，首先需要按照不同的波长范围来对两种纹理进行提取分离。利用快速傅里叶变换对3D激光扫描的方法对路面纹理进行测量后得到实际的路面剖面纹理数据进行频域转换，将其从空间域变为频域，并设计滤波器在频域内进行滤波分离，按照波长分离出宏观纹理和微观纹理。最后将滤波后的数据分别进行傅里叶逆变换，即可得到空间域的宏观纹理和微观纹理。

2.1 快速傅里叶变换

傅里叶变换在很多领域都有着广泛的应用，如数字信号处理和通信等。该分析是在空间域(或时间域)和频域之间进行转换信号，依赖于信号的类型、周期性和长度，傅里叶变换呈现多种形式[17]。离散傅里叶变换就是其一。

离散傅里叶变换(DFT)是傅里叶变换在空间域和频域上都呈现离散的形式，将空间域信号的采样变换为在离散点上傅里叶变换频域的采样。在形式上，变换序列是有限长的，而实际上这两组序列都应当被认为是离散周期信号的主值序列[18]。

设x(n)是一个长度为N的有限长序列，则x(n)的N点离散傅里叶变换定义为：

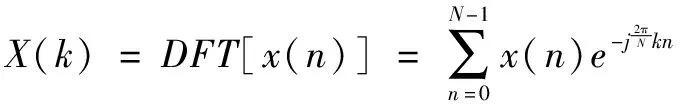
k=0,1,2,…,N-1

(1)

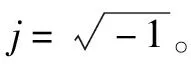
由此可见，一组实数数据经过傅里叶变换后，其结果为一组复数数据。

因为一般应用中x(n)是实数信号，此时公式可以展开为：

k=0,1,2,…,N-1

(2)

傅里叶变换的结果是该组数据所包含的信息在频域内的表达，对数据进行相关处理后，可以经过傅里叶逆变换，得到其在空间域内的表达。X(k)的离散傅里叶逆变换通过式(3)得到：

n=0,1,2,…,N-1

(3)

由离散傅里叶变换的定义式可以看出，求一个N点的离散傅里叶变换要N2次复数乘法和N(N-1)次复数加法。当N很大时，其计算量是相当大的[19]。1965年，Cooley和Tukey提出了快速傅里叶变换(FFT)的方法，实现了在实际应用中通过计算机高效快速的计算离散傅里叶变换。用快速傅里叶变换，只需Nγ/2次乘法和Nγ次加法，其中γ为log2N。从算法可以看出，与直接离散傅里叶变换相比，当N越大，快速傅里叶变换的算法效果更加明显[20]。所以本研究采用快速傅里叶变换进行数据的变换。

2.2 微观和宏观纹理的分离

本研究中的采样数据点均为三维坐标点。首先将数据进行快速傅里叶变换，将其从空间域变换到频域。傅里叶变换之后频域内结果的单位是1/mm。在分析中，要对每一个剖面上的轮廓线进行快速傅里叶变换及相关处理。

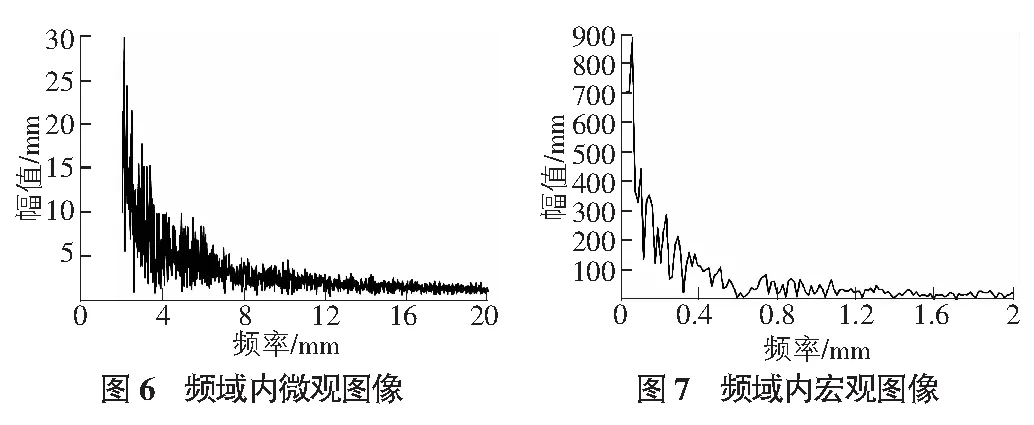
然后设计滤波器，滤波器中波长为0.05 mm～0.50 mm之间的是微观纹理构造，对应的频域为2/mm～20/mm，图6给出了频域内微观纹理对应图像；波长为0.50 mm～50.0 mm之间的是宏观纹理构造，对应的频域为0.02/mm～2/mm，图7给出了频域内宏观纹理对应图像。对剖面轮廓线频域内的按照波长进行过滤提取，就可以将宏观纹理和微观纹理在频域内进行分离。

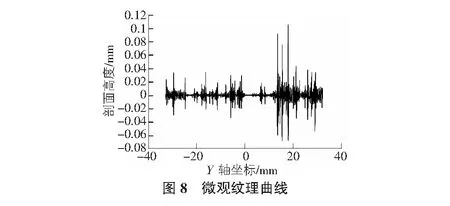
然后用傅里叶逆变换将频域内数据转换为空间域内数据，即可分别得到分离开的宏观纹理和微观纹理的空间域剖面坐标数据，分离后的微观宏观纹理图像分别如图8，图9所示。

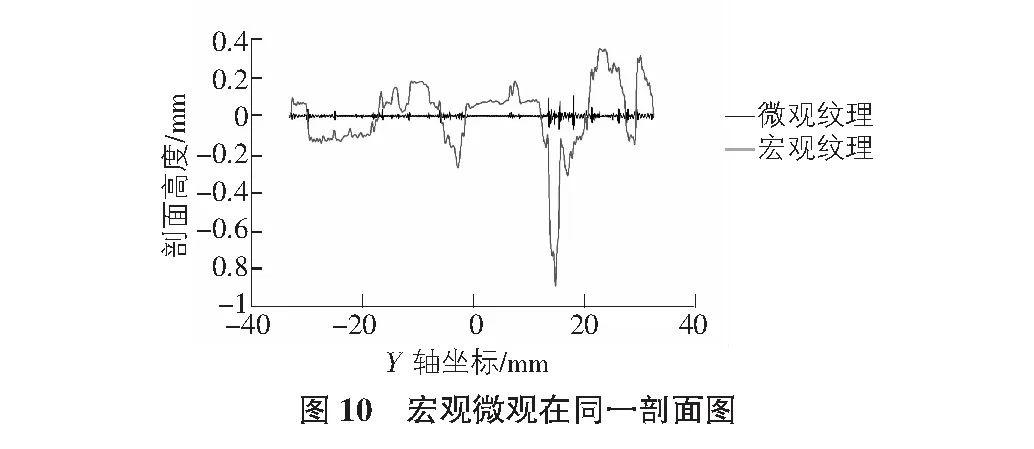
如图10所示，从同一剖面中宏观纹理和微观纹理曲线可以看到快速傅里叶变换法可以有效的将两类路面纹理进行分离。图11给出了同一剖面上的微观宏观纹理以及剖面轮廓线。从剖面轮廓线来看，宏观纹理与微观纹理的叠加与符合实际的路面纹理形态相符合。

3 结语

通过快速傅里叶变换法可以高效的分离宏观纹理与微观纹理。研究发现宏观纹理与微观纹理的叠加可以更好地表征路面纹理的实际情况。为综合考虑宏观纹理微观纹理的共同作用对道路抗滑机理研究及路面抗滑性评估提供了新方法。基于宏观纹理和微观纹理分别提出相关指标，能更全面地研究路表纹理对抗滑性能的影响，更合理地确定道路抗滑机理及抗滑性能评估方法。