大样本条件下概率阈限的改变对参数估计的影响

王风

Rasch 模型是丹麦数学家George Rasch 在1960年提出的单参数IRT 模型。 根据Rasch 模型原理，特定个体对特定题目作出特定反应的概率可以用个体能力与题目难度的简单函数来表示， 即考生能否答对某题取决于题目难度及考生能力[1]：

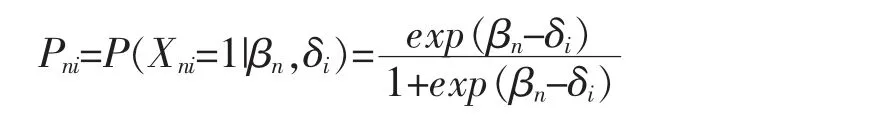
其中，βn表示考生n 的能力参数，δi表示题目i的难度参数。

当题目难度比考生能力高时， 考生倾向于采取猜答策略，尤其是水平较低的考生遇到较难题目时，往往会猜答[2]。考生能力与题目难度的差异大于2 logits时，考生会采取猜答策略，此时正确回答的概率仅为12%[3-4]。 考生猜测作答不是题目参数而是有必要消除的干扰， 作答反应中存在猜测作答会影响参数估计的准确性[5]。 因此，消除Rasch 模型中因考生猜测作答导致的统计偏差，能够提高参数估计的准确性，从而对考生能力做出更有效的推断。

一、ARRG 法理论阐述

根据Rasch 模型，在0-1 计分的题目中，若考生能力和题目难度相等，考生答对题目的概率等于0.5[6]。在4 选1 的题目中，若考生答对某题的概率小于随机猜测率（0.25），则有理由怀疑考生采取了猜答策略。

为降低Rasch 模型在估计题目难度时受考生猜测作答影响而产生的误差，Waller 提出了ARRG 法（Estimates of Ability Removing Random Guessing），经过Andrich 等人不断深入的研究，形成了相对完善的研究步骤[7-11]。

首先，ARRG 法采用Rasch 模型根据收集到的所有作答进行参数估计，称为原始分析（Original Analysis）。 其次，基于考生答对题目的概率与设定的概率阈限间的比较，当答对概率低于设定的概率阈限时，无论考生是否答对该题，均将此作答标记为缺失值，重新进行参数估计， 此过程称为裁剪分析（Tailored Analysis）。 为了使两次分析的题目难度分布有相同的原点， 要设置参数估计的约束条件， 即锚分析（Anchored Analysis）。

考生猜测作答影响题目难度和考生能力估计的准确性。题目难度估计方面，大多数题目的参数估计均受考生猜测作答的影响，尤其是较难的题目。因为题目的平均难度为0， 较难题目的难度被低估使简单题目的难度被高估[12，13]。 考生能力估计方面，较难题目的难度被低估使水平较高的考生能力被低估。Andrich 等人研究发现，考生猜测作答的存在低估了学生在学校教育中的进步， 用ARRG 法消除考生猜测作答的影响后，各个年级的成长率都有所增加，这具有重要的教育意义[14]。

Glenn 模拟了考生猜测作答在不同概率阈限（0、0.15、0.20、0.25、0.30、0.35）、 不同样本量（250、500、1000、2000）、不同猜测度（0、0.1、0.2、0.3）和不同难度条件下对难度估计的影响。 结果发现：（1）样本量比其他因素更能解释参数估计标准误的变化，当样本量较大时，所有条件下的标准误都要小得多；（2）较大的概率阈值通常与偏差减少和标准误增加有关[15]。Glenn 研究的样本量最大为2000， 随着概率阈限的增大，被标记为缺失值的作答也增加，用来估计参数的作答减少。 因此，假设当样本量较大时，标准误较小；当样本量较小时，标准误会变大。在这种思路下，尝试更大的样本量在不同概率阈限下对参数变化的影响是有意义的。

本文在Glenn 研究的基础上进一步拓宽思路，研究大样本情况下概率阈限的改变对参数估计的影响。 研究目的是通过观察不同条件下题目难度估计的变化及其标准误（SE）和数据-模型的拟合优度，探索不同样本量在不同概率阈限条件下对难度估计的影响。

ARRG 法是Rasch 模型框架下提高参数估计准确性的有效手段， 对其结果的解释又是其中重要的一环。 在小样本（250、500、1000、2000）情况下，样本量比其他因素更能解释参数估计标准误的变化，即参数估计标准误的变化可能是由样本量引起的。 若换做大样本， 参数估计标准误的变化程度如何？ 同样，在大样本情况下，较大的概率阈限是否也伴随着参数变化程度的减小和标准误的增加？ 本文试图回答以上问题， 以便为使用ARRG 法时根据样本量合理解释参数变化的意义提供参考。

二、研究方法

数据来源为某考试的作答数据， 共120 道选择题，每题4 个选项，仅有1 个正确答案，均为0-1 计分题目。 选择Winsteps 软件作为分析工具。

从总体中有放回地抽取6 个样本， 样本量分别为2000、5000、7000、10000、20000、30000。 表1 给出了6 个样本的均值、标准差、偏度和峰度，每个样本与总体的四项指标非常接近， 说明样本对总体具有一定的代表性。

表1 总体和样本的统计指标

设置5 个概率阈限，分别为：0.10、0.15、0.20、0.25、0.30， 答对概率低于概率阈限的作答会被标记为缺失值。 裁剪分析中使用的答对概率来源于原始分析。 原始分析中，原始作答包含考生猜测作答，答对概率的估计受考生猜测作答的影响，使答对概率偏高。 因此，裁剪分析中，设置概率阈限高于随机猜测率（0.25），可以更好地消除因考生猜测作答对参数估计的影响。

为使原始分析和裁剪分析的题目难度分布具有相同的原点， 将锚分析中参数估计的约束条件设置为难度接近0 的5 道题目的难度为0。

结果的检验标准有两个。 一是数据-模型的拟合：根据Rasch 模型原理，考生答对题目的概率仅由题目难度和考生能力决定。 原始作答因包含考生猜测作答导致数据-模型拟合性差。 因此假设，消除考生猜测作答对参数估计的影响后，数据-模型的拟合优度将提高。 从三个方面检验数据-模型拟合优度：个人拟合、题目拟合和χ2统计量。 二是题目难度估计的变化及其标准误（SE）。

三、结果

（一）数据-模型拟合优度

从三个方面检验数据-模型拟合优度：个人拟合、题目拟合和χ2统计量。个人拟合是指考生作答与模型预期的拟合程度；题目拟合是指题目与模型预期的拟合程度；χ2统计量则是检验Rasch 模型拟合优度的传统方法。 通过分析结果发现，在样本量相同的条件下，随着概率阈限的增大，个人拟合的程度增加，不拟合（Misfit）的考生数目下降，同时各个样本均在概率阈限为0．25 时， 不拟合的考生数目最小。 不同条件下，Winsteps 结果中均未发现不拟合的题目。 同时，题目的未加权均方拟合统计量（Outfit MNSQ）和加权均方拟合统计量（Infit MNSQ）值均在0．87～1．11 范围内，拟合程度比较好。 当样本量增加时， 标准化残差均方（Standardized as a Z-Score，ZSTD） 值随之变大，但ZSTD 统计量受样本容量影响较大，故不作为参考。

χ2和自由度有关，因此随着样本量的增加，χ2增大。但在样本量相同的条件下，χ2随着概率阈限的增大而减小。不同条件下χ2对应的P 值均为0．0000。χ2统计量的变化和个人拟合指标证明， 经过ARRG 法处理的考生作答确实提高了数据-模型拟合优度，消除了考生猜测作答对题目参数估计的影响。

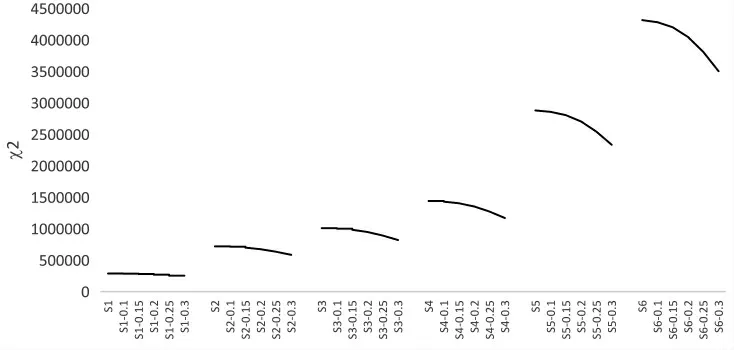
图1 不同条件下χ2 的变化

（二）难度变化

比较不同样本量、 不同概率阈限对难度估计的影响可以发现， 难度的变化主要受概率阈限的影响，受样本量的影响较小，下面以两个样本为例说明。 图2、图3 分别是样本1、6 的题目难度估计偏差。 观察图2、图3 可以看到，难度较低的题目经过调整后难度更低，但变化程度较小，概率阈限较小条件下几乎不发生变化；随着难度的增加，较难题目调整后难度更大，且变化程度较大，概率阈限越大，变化越剧烈。

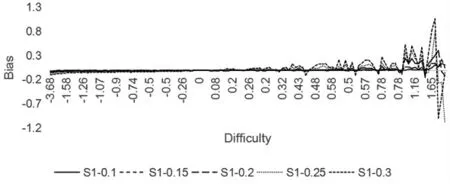
图2 样本1 的题目难度估计偏差

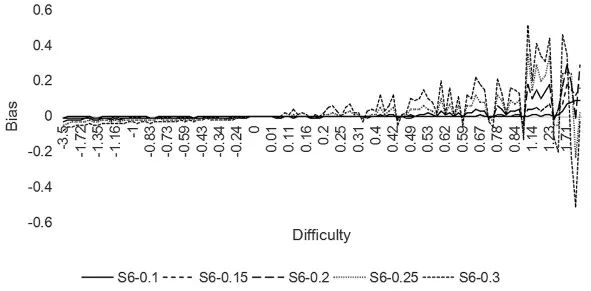
图3 样本6 的题目难度估计偏差

（三）标准误

标准误代表了参数估计的精度如何， 以下分别计算了不同条件下难度估计的标准误的均值及难度不同题目在不同条件下标准误的变化。

观察图4 可知，无论概率阈限如何变化，随着样本量的增大，难度估计的标准误逐渐减小，且标准误变化的全距逐渐缩小。 当样本量为30000（S6）时，标准误变化的全距仅为0．009。 在不同的样本中，随着概率阈限的增加，标准误的变化趋势有相似之处。概率阈限为0 时的标准误最小，概率阈限越大，标准误越大，概率阈限为0．3 时，标准误最大。 值得注意的是，样本量为2000（S1）时的标准误整体比较大，在概率阈限为0．3 时，参数估计的标准误最大，而当样本量增加到5000（S2）时，标准误整体下降比较明显。因此， 使用ARRG 法时， 若对参数估计的精度有要求，需要尽量提供较大的样本量。

均值代表了标准误变化的整体趋势。 难度不同的题目受考生猜测作答的影响不同， 经过ARRG 法处理的结果也有所不同。 为了观察不同难度题目标准误的变化，以下抽取3 道题目分别说明。

图5 为3 道难度不同题目的标准误变化， 代表了难度变化的2 种类型。 32、39、110 题的难度依次增大， 分别是-2.36、0.09 和1.94。 观察图5 可以看到，32 题和39 题的标准误变化全距不大；110 题的标准误随着样本量的增大而减小， 随着概率阈限的增加而增加，与标准误的均值变化趋势相似，变化比较剧烈。在32 题和39 题标准误的变化中，概率阈限为0.3 时，标准误的变化出现了小的波动，说明概率阈限较大时被标记为缺失值的作答增加， 用于估计参数的信息减少。因此，对高风险测验进行处理时要尽量采用大样本及合适的概率阈限， 以获得较高的参数估计精度。 难度较小的题目受考试猜测作答的影响较小，被标记为缺失值的作答较少，因此标准误的变化不明显；同时随着样本量的增加，标准误也随之降低。难度较大的题目更容易引入猜测作答，概率阈限设置的越高，被标记为缺失值的作答越多，标准误越大，小样本的变化尤为明显。

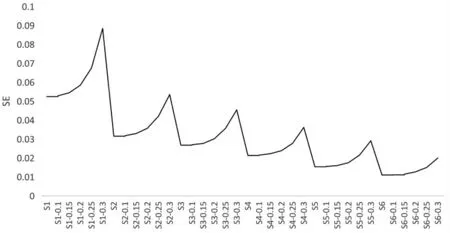
图4 不同样本量及概率阈限条件下难度估计标准误均值的变化

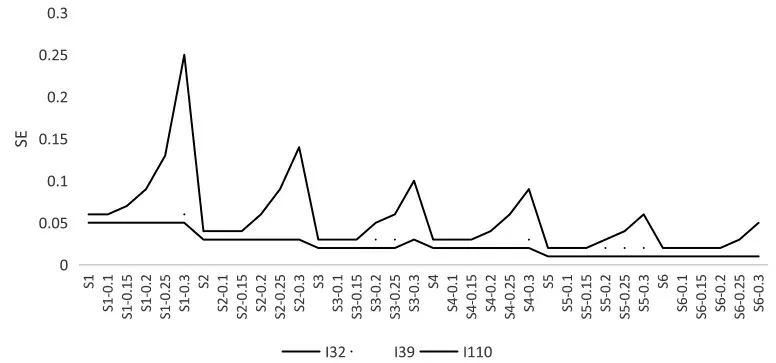
图5 不同难度题目标准误的变化

四、结论

考生猜测作答是一种偏离测验构念的行为，可以通过Rasch 模型参数变化来检验，并将与其相关的问题最小化。ARRG 法是Rasch 模型框架下消除考生猜测作答对参数估计的影响、提高参数估计准确性的有效手段。本文的研究目的是观察大样本情况下概率阈限的改变对参数估计的影响。 从两个角度验证ARRG 法的有效性：不同样本量、不同概率阈限下数据-模型的拟合优度、难度估计的变化及其标准误。

个人拟合优度主要受样本量的影响， 样本量的增加伴随着异常作答的增多， 不拟合的考生数目增加； 但在样本量相同的条件下， 随着概率阈限的增大，个人拟合优度增加，不拟合的考生数目下降，在概率阈限为0.25 时降到最小值。 χ2和个人拟合的变化趋势相似，随概率阈限的增加而降低。个人拟合优度的提高和χ2的降低说明消除考生猜测作答能明显提高数据-模型的拟合优度。

难度估计的变化主要受题目自身难度的影响，根据题目难度的不同， 难度估计的变化趋势分为两类：简单题目的难度变小，但整体变化不大；较难题目的难度变大，且随着概率阈限的增加，难度变化程度增加。 难度估计的变化受样本量的影响较小，不同样本量的题目难度变化趋势相似。 标准误的变化主要受样本量的影响，样本量较小时（2000），标准误随概率阈限的变化有较大波动；样本量逐渐增加时，即使设置较大的概率阈限（0.3），标准误的变化也很小。

大样本条件下， 概率阈限的改变主要引起题目难度估计的变化。概率阈限越大，题目难度估计的变化程度越大，但不会引起标准误的剧烈波动，相反，标准误处于比较平稳的水平。因此，在高风险测试中，若要消除考生猜测作答对参数估计的影响，应该尽量使用大样本，以保证调整过程中参数估计的精度。同时，在使用ARRG 法时，概率阈限的设置不是越大越好，个人拟合指标显示，不拟合的考生数目在概率阈限为0.25 时最低，但χ2统计量保持下降趋势，这就需要根据实际情况选择合适的概率阈限。通常会选择略高于0-1 计分题目随机猜测率的值作为概率阈限。